冀教五年级上册数学9.2图形密铺的奥秘 课件
文档属性
| 名称 | 冀教五年级上册数学9.2图形密铺的奥秘 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-28 00:00:00 | ||
图片预览





文档简介
(共24张PPT)
探索乐园
第2课时
图形密铺的奥秘
课堂导入-新知探究-课堂练习-课堂小结-课堂作业
冀教版
数学
五年级
上册
1.通过观察生活中常见的密铺现象,知道什么是平面图形的密铺;通过拼摆各种图形,探索密铺的特点,从而认识一些可以密铺的平面图形。
2.经历欣赏密铺图案,用图形密铺以及探究密铺奥秘的过程,提升学生观察、猜测、验证、推理和交流的能力,发展合理推理能力和空间观念。
3.积极参加数学活动,获得探索密铺奥秘的愉快体验,激发学生学习数学的兴趣,享受由美带来的愉悦。
你们能不能说一说这些美丽的拼图有什么特点?
你知道什么叫做密铺吗?
无论是什么形状的地砖,只要可以将一块地面的中间既不留空隙,也不重叠地铺满,就是密铺。
密铺。
用下面的图形可以密铺吗?
等边三角形
正六边形
正八边形
用下面的图形可以密铺吗?
长方形
正五边形
圆形
小组合作要求:
图形
是否能密铺
1.小组分工合作,每人选一种图形进行研究。
2.把你铺的结果粘在纸上并与组内同学交流。
密铺中到底有什么奥秘?
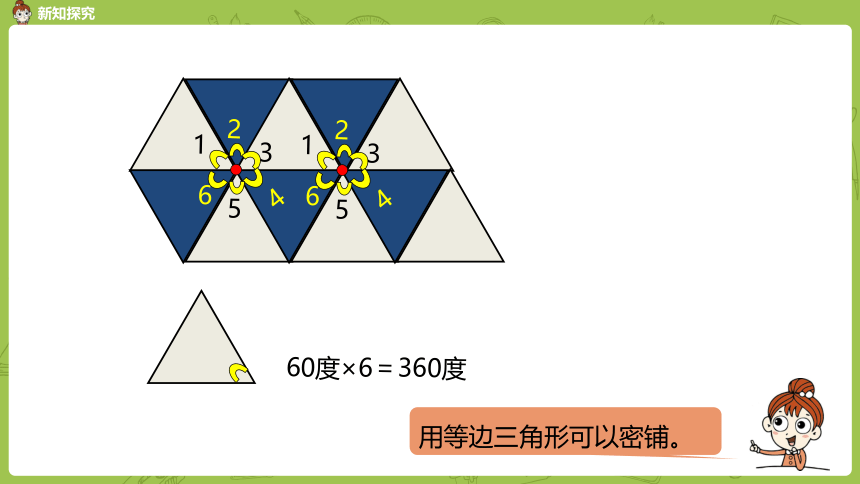
用等边三角形可以密铺。
1
2
3
4
5
6
1
2
3
4
5
6
60度
×6
=360度
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
120度
×3
=360度
120度
用正六边形也可以密铺。
正五边形不可以密铺。
正五边形不可以密铺。
1
2
3
108度
×(
?)
≠360度
108度
小组合作要求:
图形
是否能密铺
1.小组分工合作,每人选一种图形进行研究。
2.把你铺的结果粘在纸上并与组内同学交流。
√
√
√
×
×
×
密铺中到底有什么奥秘?
通过我们的实验可以发现:一个多边形,如果几个角能组成360度,则可以密铺,否则将无法进行密铺。
思考:
怎样的图形才可以密铺?
图形
是否能密铺
√
√
√
×
×
×
1
下面三幅图中,哪幅图可以密铺?为什么?
第3幅图。因为密铺既不留空隙,也不重叠,只有第3幅图符合。
艺术都源于生活,所以艺术家的作品都源于生活,我们接下来要欣赏的就是生活中的美丽密铺。
艺术都源于生活,所以艺术家的作品都源于生活,我们接下来要欣赏的就是生活中的美丽密铺。
艺术都源于生活,所以艺术家的作品都源于生活,我们接下来要欣赏的就是生活中的美丽密铺。
艺术都源于生活,所以艺术家的作品都源于生活,我们接下来要欣赏的就是生活中的美丽密铺。
1.几个正多边形的一个内角加在一起成为一个周角时,这几个正多边形就可以进行密铺。
2.在所有的正多边形中,只有正三角形、长方形、正方形、正六边形可以密铺(单一正多边形密铺);形状、大小完全相同的任意四边形能密铺;圆不能密铺。
1
选择题。
(1)下列图形中,不能密铺的是( )。
(2)下面的正多边形中,( )不能密铺。
A.正三角形
B.正方形
C.正六边形
D.正八边形
B
D
1
选择题。
(3)下列关于密铺的说法正确的是( )。
D
A.边数为单数的多边形都不能密铺
B.凡是完全相同的正多边形都可以密铺
C.不是正多边形就不能密铺
D.凡是完全相同的平行四边形都能密铺
1
选择题。
(4)形状、大小完全相同的( )能密铺。
D
A.圆
B.正八边形
C.正七边形
D.梯形
(5)贝贝家客厅的长是6米,宽是4.8米。准备在地面上铺方砖,要求地面上都是整块方砖,应该选择( )的方砖。
B
A.边长为50厘米
B.边长为60厘米
C.边长为100厘米
D.以上都不对
正八边形地砖和哪种瓷砖配合使用,就能密铺呢?
2
正四边形的内角是90度,,正八边形的内角是135度,
这样两个正八边形和一个正四边形的内角和就是135ⅹ2+90=270+90=360度,所以可以密铺!
135度
探索乐园
第2课时
图形密铺的奥秘
课堂导入-新知探究-课堂练习-课堂小结-课堂作业
冀教版
数学
五年级
上册
1.通过观察生活中常见的密铺现象,知道什么是平面图形的密铺;通过拼摆各种图形,探索密铺的特点,从而认识一些可以密铺的平面图形。
2.经历欣赏密铺图案,用图形密铺以及探究密铺奥秘的过程,提升学生观察、猜测、验证、推理和交流的能力,发展合理推理能力和空间观念。
3.积极参加数学活动,获得探索密铺奥秘的愉快体验,激发学生学习数学的兴趣,享受由美带来的愉悦。
你们能不能说一说这些美丽的拼图有什么特点?
你知道什么叫做密铺吗?
无论是什么形状的地砖,只要可以将一块地面的中间既不留空隙,也不重叠地铺满,就是密铺。
密铺。
用下面的图形可以密铺吗?
等边三角形
正六边形
正八边形
用下面的图形可以密铺吗?
长方形
正五边形
圆形
小组合作要求:
图形
是否能密铺
1.小组分工合作,每人选一种图形进行研究。
2.把你铺的结果粘在纸上并与组内同学交流。
密铺中到底有什么奥秘?
用等边三角形可以密铺。
1
2
3
4
5
6
1
2
3
4
5
6
60度
×6
=360度
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
120度
×3
=360度
120度
用正六边形也可以密铺。
正五边形不可以密铺。
正五边形不可以密铺。
1
2
3
108度
×(
?)
≠360度
108度
小组合作要求:
图形
是否能密铺
1.小组分工合作,每人选一种图形进行研究。
2.把你铺的结果粘在纸上并与组内同学交流。
√
√
√
×
×
×
密铺中到底有什么奥秘?
通过我们的实验可以发现:一个多边形,如果几个角能组成360度,则可以密铺,否则将无法进行密铺。
思考:
怎样的图形才可以密铺?
图形
是否能密铺
√
√
√
×
×
×
1
下面三幅图中,哪幅图可以密铺?为什么?
第3幅图。因为密铺既不留空隙,也不重叠,只有第3幅图符合。
艺术都源于生活,所以艺术家的作品都源于生活,我们接下来要欣赏的就是生活中的美丽密铺。
艺术都源于生活,所以艺术家的作品都源于生活,我们接下来要欣赏的就是生活中的美丽密铺。
艺术都源于生活,所以艺术家的作品都源于生活,我们接下来要欣赏的就是生活中的美丽密铺。
艺术都源于生活,所以艺术家的作品都源于生活,我们接下来要欣赏的就是生活中的美丽密铺。
1.几个正多边形的一个内角加在一起成为一个周角时,这几个正多边形就可以进行密铺。
2.在所有的正多边形中,只有正三角形、长方形、正方形、正六边形可以密铺(单一正多边形密铺);形状、大小完全相同的任意四边形能密铺;圆不能密铺。
1
选择题。
(1)下列图形中,不能密铺的是( )。
(2)下面的正多边形中,( )不能密铺。
A.正三角形
B.正方形
C.正六边形
D.正八边形
B
D
1
选择题。
(3)下列关于密铺的说法正确的是( )。
D
A.边数为单数的多边形都不能密铺
B.凡是完全相同的正多边形都可以密铺
C.不是正多边形就不能密铺
D.凡是完全相同的平行四边形都能密铺
1
选择题。
(4)形状、大小完全相同的( )能密铺。
D
A.圆
B.正八边形
C.正七边形
D.梯形
(5)贝贝家客厅的长是6米,宽是4.8米。准备在地面上铺方砖,要求地面上都是整块方砖,应该选择( )的方砖。
B
A.边长为50厘米
B.边长为60厘米
C.边长为100厘米
D.以上都不对
正八边形地砖和哪种瓷砖配合使用,就能密铺呢?
2
正四边形的内角是90度,,正八边形的内角是135度,
这样两个正八边形和一个正四边形的内角和就是135ⅹ2+90=270+90=360度,所以可以密铺!
135度
