2021—2022学年沪科版数学八年级上册15.4 角的平分线 课时练习(word版含答案)
文档属性
| 名称 | 2021—2022学年沪科版数学八年级上册15.4 角的平分线 课时练习(word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 88.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-29 00:00:00 | ||
图片预览


文档简介
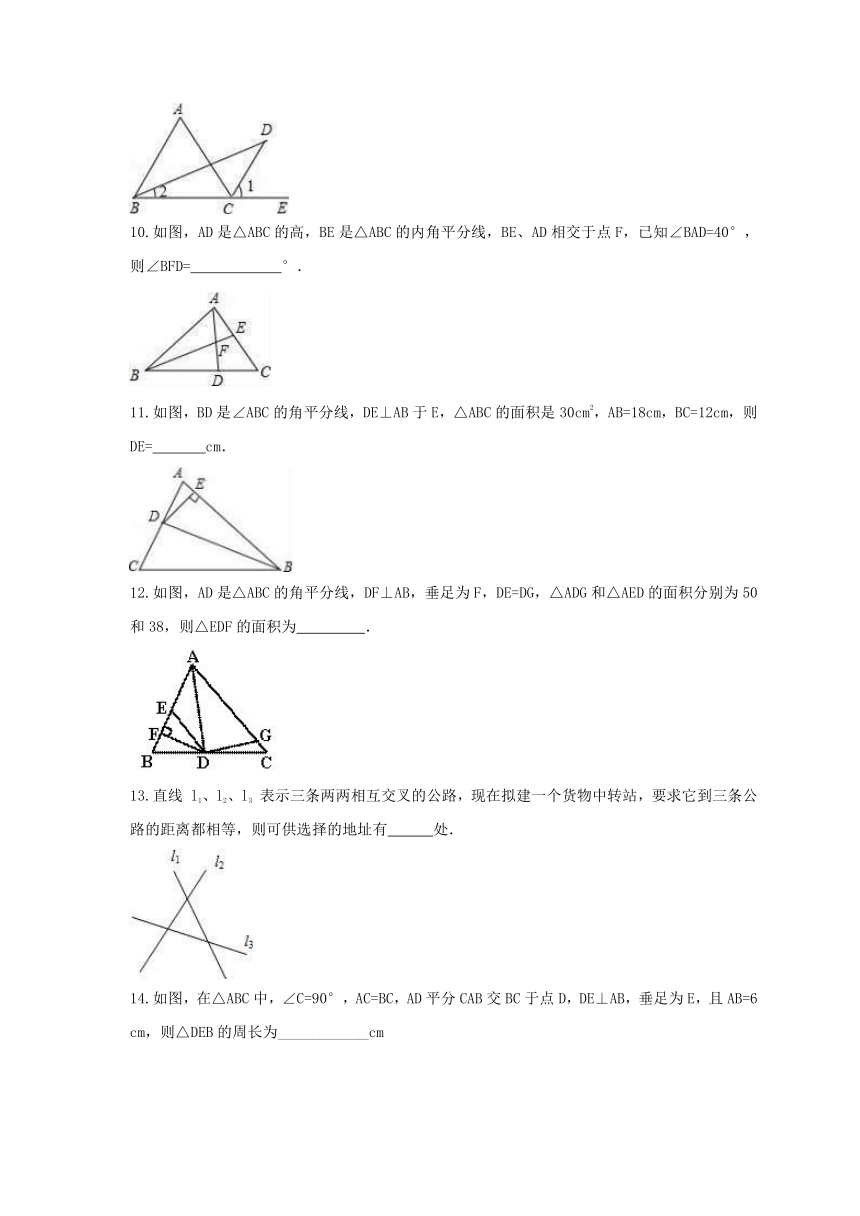
沪科版数学八年级上册
15.4《角的平分线》课时练习
一、选择题
1.如图,在△ABC中,∠A=50°,∠ABC=70°,BD平分∠ABC,则∠BDC的度数是(
)
A.85°
B.80°
C.75°
D.70°
2.如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A=(
)
A.35°
B.95°
C.85°
D.75°
3.如图,△ABC中,AD为△ABC的角平分线,BE为△ABC的高,∠C=70°,∠ABC=48°,那么∠3是(?
)
A.59°?????
B.60°??????
C.56°?????
D.22°
4.如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠ADE的大小是(?
???)
?
A.45°????
???
B.54°???
??
C.40°???
???
D.50°
5.如图,在△ACB中,∠ACB=100°,∠A=20°,D是AB上一点.将△ABC沿CD折叠,使B点落在AC边上的B′处,则∠ADB′等于(
)
A.25°
B.30°
C.35°
D.40°
6.如图,OP是∠AOB的平分线,点P到OA的距离为3,点N是OB上的任意一点,则线段PN的取值范围为(
)
A.PN<3
B.PN>3
C.PN≥3
D.PN≤3
7.如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于(
)
A.10
B.7
C.5
D.4
8.如图,在△ABC中,AB=AC=4,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC分别交AB、AC于M、N,则△AMN的周长为(
)
A.12
B.4
C.8
D.不确定
二、填空题
9.如图在△ABC中,∠A=50°,∠ABC的角平分线与∠ACB的外角平分线交于点D,则∠D的度数为 .
10.如图,AD是△ABC的高,BE是△ABC的内角平分线,BE、AD相交于点F,已知∠BAD=40°,则∠BFD= °.
11.如图,BD是∠ABC的角平分线,DE⊥AB于E,△ABC的面积是30cm2,AB=18cm,BC=12cm,则DE=
cm.
12.如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和38,则△EDF的面积为?
???.
13.直线
l1、l2、l3
表示三条两两相互交叉的公路,现在拟建一个货物中转站,要求它到三条公路的距离都相等,则可供选择的地址有
处.
14.如图,在△ABC中,∠C=90°,AC=BC,AD平分CAB交BC于点D,DE⊥AB,垂足为E,且AB=6
cm,则△DEB的周长为____________cm
三、解答题
15.如图,在△ABC中,CD⊥AB于点D,CE是∠ACB的平分线,∠A=20°,∠B=60°,
求∠BCD和∠ECD的度数.
16.如图,在△ABC中,AD是高线,AE,BF是角平分线,它们相交于点O,∠CAB=50°,
∠C=60°,求∠DAE和∠BOA的度数.
17.如图,已知:CD⊥AB于D,BE⊥AC于E,且BD=CE,BE交CD于点O.求证:AO平分∠BAC.
18.如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF,
(1)求证:AD平分∠BAC;
(2)已知AC=20,
BE=4,求AB的长.
参考答案
1.A
2.C
3.B
4.C
5.D
6.C
7.C
8.C
9.答案为:25°.
10.答案为:65°.
11.答案为:2.
12.答案为:6;
13.答案为:4.
14.答案为:6;
15.解:∵CD⊥AB,∴∠CDB=90°.
∵∠B=60°,
∴∠BCD=180°-∠CDB-∠B=30°.
∵∠A=20°,∠B=60°,∠A+∠B+∠ACB=180°,
∴∠ACB=100°.
∵CE是∠ACB的平分线,
∴∠BCE=∠ACB=50°,
∴∠ECD=∠BCE-∠BCD=20°.
16.解:∵∠CAB=50°,∠C=60°,
∴∠ABC=180°-50°-60°=70°.
∵AD是高线,∴∠ADC=90°,
∴∠DAC=180°-∠ADC-∠C=30°.
∵AE,BF是角平分线,
∴∠ABF=∠ABC=35°,∠EAF=∠CAB=25°,
∴∠DAE=∠DAC-∠EAF=5°,
∠AFB=180°-∠ABF-∠CAB=95°,
∴∠AOF=180°-∠AFB-∠EAF=60°,
∴∠BOA=180°-∠AOF=120°.
17.证明:∵OD⊥AB,OE⊥AC∴∠BDO=∠CEO=90°,
又∵∠BOD=∠COE,BD=CE,∴△BOD≌△COE∴OD=OE
又由已知条件得△AOD和△AOE都是Rt△,且OD=OE,OA=OA,
∴Rt△AOD≌Rt△AOE.∴∠DAO=∠EAO,即AO平分∠BAC.
18.(1)证明:∵DE⊥AB,DF⊥AC,
∴∠E=∠DFC=90°,
∴在Rt△BED和Rt△CFD中
BD=CD,BE=CF.
∴Rt△BED≌Rt△CFD(HL),
∴DE=DF,
∵DE⊥AB,DF⊥AC,
∴AD平分∠BAC;
(2)解:∵Rt△BED≌Rt△CFD,
∴AE=AF,CF=BE=4,
∵AC=20,
∴AE=AF=20﹣4=16,
∴AB=AE﹣BE=16﹣4=12.
15.4《角的平分线》课时练习
一、选择题
1.如图,在△ABC中,∠A=50°,∠ABC=70°,BD平分∠ABC,则∠BDC的度数是(
)
A.85°
B.80°
C.75°
D.70°
2.如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A=(
)
A.35°
B.95°
C.85°
D.75°
3.如图,△ABC中,AD为△ABC的角平分线,BE为△ABC的高,∠C=70°,∠ABC=48°,那么∠3是(?
)
A.59°?????
B.60°??????
C.56°?????
D.22°
4.如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠ADE的大小是(?
???)
?
A.45°????
???
B.54°???
??
C.40°???
???
D.50°
5.如图,在△ACB中,∠ACB=100°,∠A=20°,D是AB上一点.将△ABC沿CD折叠,使B点落在AC边上的B′处,则∠ADB′等于(
)
A.25°
B.30°
C.35°
D.40°
6.如图,OP是∠AOB的平分线,点P到OA的距离为3,点N是OB上的任意一点,则线段PN的取值范围为(
)
A.PN<3
B.PN>3
C.PN≥3
D.PN≤3
7.如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于(
)
A.10
B.7
C.5
D.4
8.如图,在△ABC中,AB=AC=4,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC分别交AB、AC于M、N,则△AMN的周长为(
)
A.12
B.4
C.8
D.不确定
二、填空题
9.如图在△ABC中,∠A=50°,∠ABC的角平分线与∠ACB的外角平分线交于点D,则∠D的度数为 .
10.如图,AD是△ABC的高,BE是△ABC的内角平分线,BE、AD相交于点F,已知∠BAD=40°,则∠BFD= °.
11.如图,BD是∠ABC的角平分线,DE⊥AB于E,△ABC的面积是30cm2,AB=18cm,BC=12cm,则DE=
cm.
12.如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和38,则△EDF的面积为?
???.
13.直线
l1、l2、l3
表示三条两两相互交叉的公路,现在拟建一个货物中转站,要求它到三条公路的距离都相等,则可供选择的地址有
处.
14.如图,在△ABC中,∠C=90°,AC=BC,AD平分CAB交BC于点D,DE⊥AB,垂足为E,且AB=6
cm,则△DEB的周长为____________cm
三、解答题
15.如图,在△ABC中,CD⊥AB于点D,CE是∠ACB的平分线,∠A=20°,∠B=60°,
求∠BCD和∠ECD的度数.
16.如图,在△ABC中,AD是高线,AE,BF是角平分线,它们相交于点O,∠CAB=50°,
∠C=60°,求∠DAE和∠BOA的度数.
17.如图,已知:CD⊥AB于D,BE⊥AC于E,且BD=CE,BE交CD于点O.求证:AO平分∠BAC.
18.如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF,
(1)求证:AD平分∠BAC;
(2)已知AC=20,
BE=4,求AB的长.
参考答案
1.A
2.C
3.B
4.C
5.D
6.C
7.C
8.C
9.答案为:25°.
10.答案为:65°.
11.答案为:2.
12.答案为:6;
13.答案为:4.
14.答案为:6;
15.解:∵CD⊥AB,∴∠CDB=90°.
∵∠B=60°,
∴∠BCD=180°-∠CDB-∠B=30°.
∵∠A=20°,∠B=60°,∠A+∠B+∠ACB=180°,
∴∠ACB=100°.
∵CE是∠ACB的平分线,
∴∠BCE=∠ACB=50°,
∴∠ECD=∠BCE-∠BCD=20°.
16.解:∵∠CAB=50°,∠C=60°,
∴∠ABC=180°-50°-60°=70°.
∵AD是高线,∴∠ADC=90°,
∴∠DAC=180°-∠ADC-∠C=30°.
∵AE,BF是角平分线,
∴∠ABF=∠ABC=35°,∠EAF=∠CAB=25°,
∴∠DAE=∠DAC-∠EAF=5°,
∠AFB=180°-∠ABF-∠CAB=95°,
∴∠AOF=180°-∠AFB-∠EAF=60°,
∴∠BOA=180°-∠AOF=120°.
17.证明:∵OD⊥AB,OE⊥AC∴∠BDO=∠CEO=90°,
又∵∠BOD=∠COE,BD=CE,∴△BOD≌△COE∴OD=OE
又由已知条件得△AOD和△AOE都是Rt△,且OD=OE,OA=OA,
∴Rt△AOD≌Rt△AOE.∴∠DAO=∠EAO,即AO平分∠BAC.
18.(1)证明:∵DE⊥AB,DF⊥AC,
∴∠E=∠DFC=90°,
∴在Rt△BED和Rt△CFD中
BD=CD,BE=CF.
∴Rt△BED≌Rt△CFD(HL),
∴DE=DF,
∵DE⊥AB,DF⊥AC,
∴AD平分∠BAC;
(2)解:∵Rt△BED≌Rt△CFD,
∴AE=AF,CF=BE=4,
∵AC=20,
∴AE=AF=20﹣4=16,
∴AB=AE﹣BE=16﹣4=12.
