2021-2022学年沪科版数学八年级上册15.2 线段的垂直平分线 课时练习 (word版含答案)
文档属性
| 名称 | 2021-2022学年沪科版数学八年级上册15.2 线段的垂直平分线 课时练习 (word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 102.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-29 16:42:03 | ||
图片预览


文档简介
沪科版数学八年级上册
15.2《线段的垂直平分线》课时练习
一、选择题
1.如图,AC=AD,BC=BD,则有(???
)
A.AB垂直平分CD
B.CD垂直平分AB
C.AB与CD互相垂直平分
D.CD平分∠ACB
2.如图,MN是线段AB的垂直平分线,C在MN外,且与A点在MN的同一侧,BC交MN于P点,则( )
A.BC>PC+AP???
B.BC<PC+AP?
C.BC=PC+AP??
D.BC≥PC+AP
3.如图,在Rt△ABC中,∠B=90°,以点A为圆心,适当长为半径画弧,分别交AB、AC于点D,E,再分别以点D、E为圆心,大于DE为半径画弧,两弧交于点F,作射线AF交边BC于点G,若BG=1,AC=4,则△ACG的面积是( )
A.1???
???
B.1.5?
?
??
C.2???
???
D.2.5
4.如图,已知线段AB,分别以点A、点B为圆心,以大于AB的长为半径画弧,两弧交于点C和点D,作直线CD,在CD上取两点P、M,连接PA、PB、MA、MB,则下列结论一定正确的是( )
A.PA=MA????
??
B.MA=PE???
???
C.PE=BE????
???
D.PA=PB
5.在Rt△ABC中,∠A=40°,∠B=90°,AC的垂直平分线MN分别与AB,AC交于点D,E,则∠BCD的度数为( )
A.10°
B.15°
C.40°
D.50°
6.如图,在Rt△ABC中,∠C=90°,边AB的垂直平分线交AC于点D,交AB于点E.若BC=4,AC=8,则BD=(
)
A.3
B.4
C.5
D.6
7.如图所示,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A、B,下列结论不一定成立的是(
)
A.PA=PB
B.OA=OB
C.PO平分∠APB
D.AB垂直平分OP
8.如图,A,B,C表示三个居民小区,为丰富居民们的文化生活,现准备建一个文化广场,使它到三个小区的距离相等,则文化广场应建在(
)
A.AC,BC两边高线的交点处
B.AC,BC两边中线的交点处
C.AC,BC两边垂直平分线的交点处
D.∠A,∠B两内角平分线的交点处
二、填空题
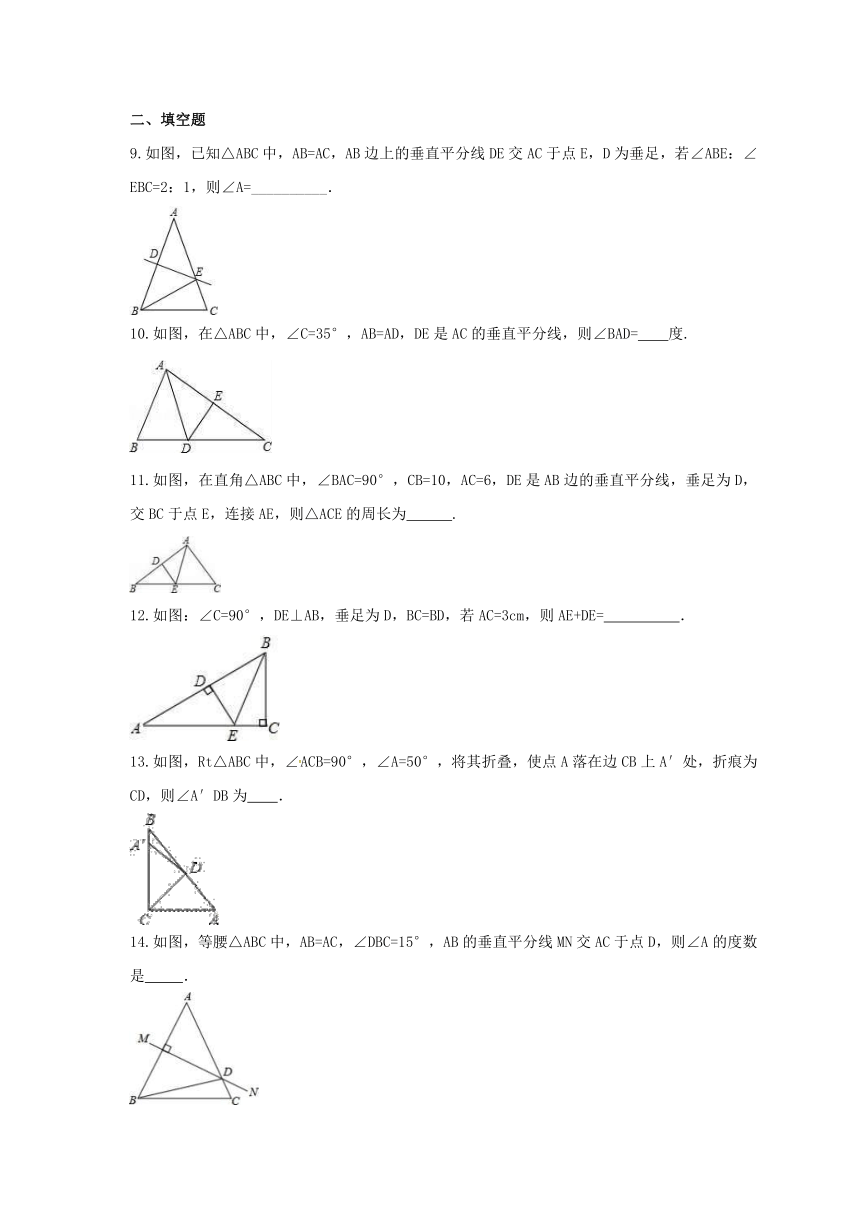
9.如图,已知△ABC中,AB=AC,AB边上的垂直平分线DE交AC于点E,D为垂足,若∠ABE:∠EBC=2:1,则∠A=__________.
10.如图,在△ABC中,∠C=35°,AB=AD,DE是AC的垂直平分线,则∠BAD= 度.
11.如图,在直角△ABC中,∠BAC=90°,CB=10,AC=6,DE是AB边的垂直平分线,垂足为D,交BC于点E,连接AE,则△ACE的周长为
.
12.如图:∠C=90°,DE⊥AB,垂足为D,BC=BD,若AC=3cm,则AE+DE=
.
13.如图,Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB为 .
14.如图,等腰△ABC中,AB=AC,∠DBC=15°,AB的垂直平分线MN交AC于点D,则∠A的度数是
.
三、解答题
15.如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,F,连接EF,EF与AD相交于点G.
求证:AD是EF的垂直平分线.
16.如图,已知△ABC,AB=AC,AD是△ABC角平分线,EF垂直平分AC,分别交AC,AD,AB于点E,O,F.若∠CAD=20°,求∠OCD的度数.
17.如图,在Rt△ABC中,∠C=90°,AB的中垂线DE交BC于点D,垂足为E,
且∠CAD∶∠CAB=1∶3,求∠B的度数.
18.如图,在△ABC中,°,AD是∠BAC的角平分线,EF垂直平分AD,交BC的延长线于点F.求∠FAC的大小.
参考答案
1.答案为:A
2.答案为:C.
3.答案为:C.
4.答案为:D.
5.答案为:A
6.答案为:C
7.答案为:D
8.答案为:C
9.答案为:45°
10.答案为:40.
11.答案为:16
12.答案为:3cm;
13.答案为:10°.
14.答案为:50°.
15.证明:∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,
∴DE=DF,∠AED=∠AFD=90°,
在Rt△AED和Rt△AFD中
AD=AD,DE=DF.
∴Rt△AED≌Rt△AFD,
∴AE=AF,
∵DE=DF,A、D为不同的点,
∴直线AD是EF的垂直平分线,
∴AD垂直平分EF.
16.50°
17.解:设∠CAD=x°,
则∠CAB=3x°,∠BAD=2x°.
∵DE是AB的中垂线,
∴DA=DB,
∴∠B=∠BAD=2x°.
∵∠C=90°,
∴∠CAB+∠B=90°,
即3x+2x=90,
解得x=18,
∴∠B=2×18°=36°.
18.解:∵EF垂直平分AD?∴FA=FD
∴∠ADF=∠DAF
??
又∵∠ADF=∠B+∠BAD,∠DAF=∠FAC+∠DAC,∠BAD=∠DAC
∴∠FAC=∠B=45°
15.2《线段的垂直平分线》课时练习
一、选择题
1.如图,AC=AD,BC=BD,则有(???
)
A.AB垂直平分CD
B.CD垂直平分AB
C.AB与CD互相垂直平分
D.CD平分∠ACB
2.如图,MN是线段AB的垂直平分线,C在MN外,且与A点在MN的同一侧,BC交MN于P点,则( )
A.BC>PC+AP???
B.BC<PC+AP?
C.BC=PC+AP??
D.BC≥PC+AP
3.如图,在Rt△ABC中,∠B=90°,以点A为圆心,适当长为半径画弧,分别交AB、AC于点D,E,再分别以点D、E为圆心,大于DE为半径画弧,两弧交于点F,作射线AF交边BC于点G,若BG=1,AC=4,则△ACG的面积是( )
A.1???
???
B.1.5?
?
??
C.2???
???
D.2.5
4.如图,已知线段AB,分别以点A、点B为圆心,以大于AB的长为半径画弧,两弧交于点C和点D,作直线CD,在CD上取两点P、M,连接PA、PB、MA、MB,则下列结论一定正确的是( )
A.PA=MA????
??
B.MA=PE???
???
C.PE=BE????
???
D.PA=PB
5.在Rt△ABC中,∠A=40°,∠B=90°,AC的垂直平分线MN分别与AB,AC交于点D,E,则∠BCD的度数为( )
A.10°
B.15°
C.40°
D.50°
6.如图,在Rt△ABC中,∠C=90°,边AB的垂直平分线交AC于点D,交AB于点E.若BC=4,AC=8,则BD=(
)
A.3
B.4
C.5
D.6
7.如图所示,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A、B,下列结论不一定成立的是(
)
A.PA=PB
B.OA=OB
C.PO平分∠APB
D.AB垂直平分OP
8.如图,A,B,C表示三个居民小区,为丰富居民们的文化生活,现准备建一个文化广场,使它到三个小区的距离相等,则文化广场应建在(
)
A.AC,BC两边高线的交点处
B.AC,BC两边中线的交点处
C.AC,BC两边垂直平分线的交点处
D.∠A,∠B两内角平分线的交点处
二、填空题
9.如图,已知△ABC中,AB=AC,AB边上的垂直平分线DE交AC于点E,D为垂足,若∠ABE:∠EBC=2:1,则∠A=__________.
10.如图,在△ABC中,∠C=35°,AB=AD,DE是AC的垂直平分线,则∠BAD= 度.
11.如图,在直角△ABC中,∠BAC=90°,CB=10,AC=6,DE是AB边的垂直平分线,垂足为D,交BC于点E,连接AE,则△ACE的周长为
.
12.如图:∠C=90°,DE⊥AB,垂足为D,BC=BD,若AC=3cm,则AE+DE=
.
13.如图,Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB为 .
14.如图,等腰△ABC中,AB=AC,∠DBC=15°,AB的垂直平分线MN交AC于点D,则∠A的度数是
.
三、解答题
15.如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,F,连接EF,EF与AD相交于点G.
求证:AD是EF的垂直平分线.
16.如图,已知△ABC,AB=AC,AD是△ABC角平分线,EF垂直平分AC,分别交AC,AD,AB于点E,O,F.若∠CAD=20°,求∠OCD的度数.
17.如图,在Rt△ABC中,∠C=90°,AB的中垂线DE交BC于点D,垂足为E,
且∠CAD∶∠CAB=1∶3,求∠B的度数.
18.如图,在△ABC中,°,AD是∠BAC的角平分线,EF垂直平分AD,交BC的延长线于点F.求∠FAC的大小.
参考答案
1.答案为:A
2.答案为:C.
3.答案为:C.
4.答案为:D.
5.答案为:A
6.答案为:C
7.答案为:D
8.答案为:C
9.答案为:45°
10.答案为:40.
11.答案为:16
12.答案为:3cm;
13.答案为:10°.
14.答案为:50°.
15.证明:∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,
∴DE=DF,∠AED=∠AFD=90°,
在Rt△AED和Rt△AFD中
AD=AD,DE=DF.
∴Rt△AED≌Rt△AFD,
∴AE=AF,
∵DE=DF,A、D为不同的点,
∴直线AD是EF的垂直平分线,
∴AD垂直平分EF.
16.50°
17.解:设∠CAD=x°,
则∠CAB=3x°,∠BAD=2x°.
∵DE是AB的中垂线,
∴DA=DB,
∴∠B=∠BAD=2x°.
∵∠C=90°,
∴∠CAB+∠B=90°,
即3x+2x=90,
解得x=18,
∴∠B=2×18°=36°.
18.解:∵EF垂直平分AD?∴FA=FD
∴∠ADF=∠DAF
??
又∵∠ADF=∠B+∠BAD,∠DAF=∠FAC+∠DAC,∠BAD=∠DAC
∴∠FAC=∠B=45°
