2021-2022学年沪科版九年级数学上册21.4二次函数的应用练习(Word版,含答案)
文档属性
| 名称 | 2021-2022学年沪科版九年级数学上册21.4二次函数的应用练习(Word版,含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 103.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-29 23:28:27 | ||
图片预览




文档简介
二次函数的应用
某商店销售一种成本为每件40元的玩具,若按每件50元销售,一个月可售出500件,售价每涨1元,月销量就减少10件设售价为每件元,月销量为y件,月销售利润为w元.
写出y与x的函数解析式和w与x的函数解析式
商店要在月销售成本不超过10000元的情况下,使月销售利润达到8000元,售价应定为每件多少元
当售价定为每件多少元时会获得最大利润求出最大利润.
某超市购进一种商品,进货单价为10元,在销售过程中,超市规定,销售单价不低于10元且不高于19元如果该商品的销售单价单位:元与日销售量单位:件满足一次函数关系式,设该商品的日销售利润为w元,那么当该商品的销售单价单位:元定为多少时,日销售利润最大最大利润是多少元
某超市经销一种商品,每千克成本为50元经试销发现,该种商品每天的销售量千克与销售价元千克满足一次函数关系,其每天销售价、销售量的四组对应值如下表所示:
销售价元千克
55
60
65
70
销售量千克
70
60
50
40
求千克与元千克之间的函数表达式
为保证某天获得600元的销售利润,则该天的销售价应定为多少
当销售价定为多少时,才能使当天的销售利润最大最大利润是多少
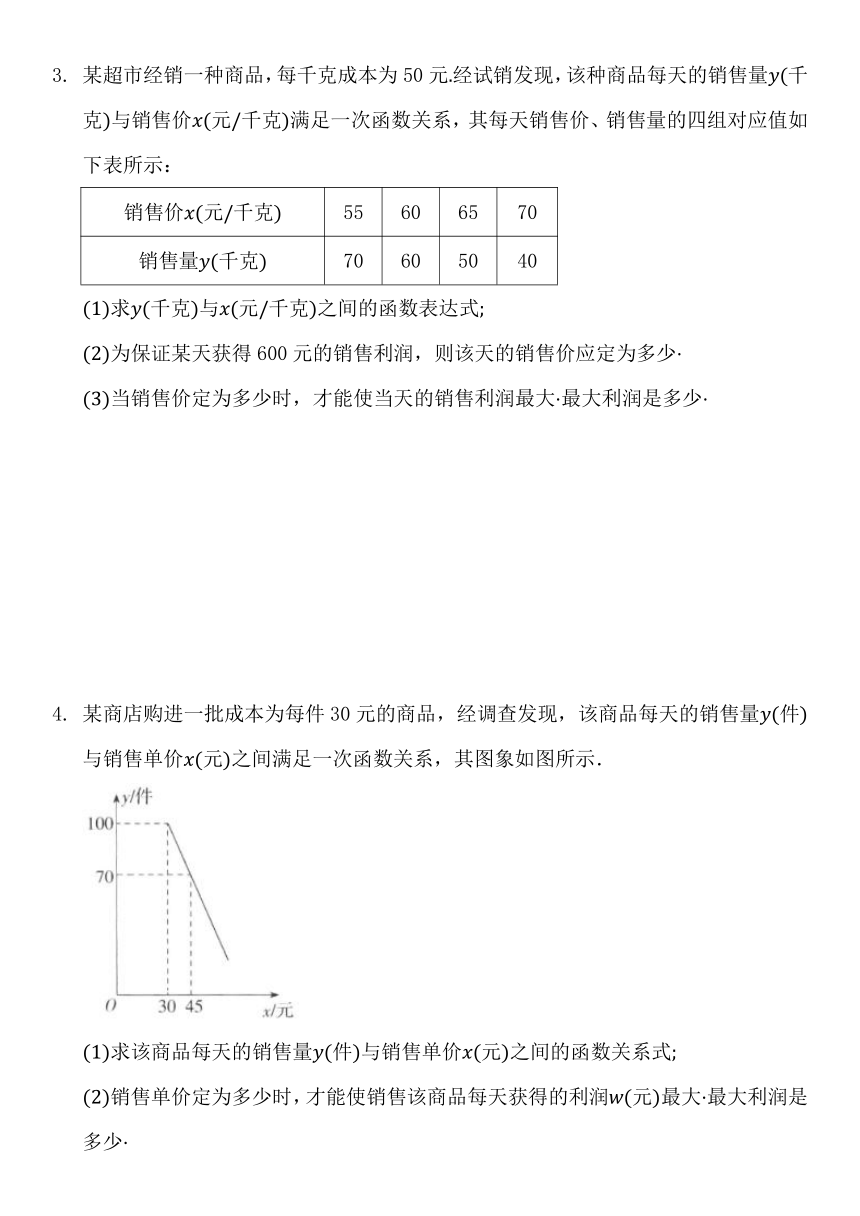
某商店购进一批成本为每件30元的商品,经调查发现,该商品每天的销售量件与销售单价元之间满足一次函数关系,其图象如图所示.
求该商品每天的销售量件与销售单价元之间的函数关系式
销售单价定为多少时,才能使销售该商品每天获得的利润元最大最大利润是多少
若该商店想使销售该商品每天获得的利润不低于800元,请直接写出此时x的取值范围.
某次足球比赛,队员甲在前场给队友乙掷界外球.如图所示:已知两人相距8米,足球出手时的高度为米,运行的路线是抛物线,当足球运行的水平距离为2米时,足球达到最大高度4米.请你根据图中所建坐标系,求出抛物线的表达式.
黔东南州某超市购进甲、乙两种商品,已知购进3件甲商品和2件乙商品,需60元;购进2件甲商品和3件乙商品,需65元.
甲、乙两种商品的进货单价分别是多少?
设甲商品的销售单价为单位:元件,在销售过程中发现:当时,甲商品的日销售量单位:件与销售单价x之间存在一次函数关系,x、y之间的部分数值对应关系如表:
销售单价元件
11
19
日销售量件
18
2
请写出当时,y与x之间的函数关系式.
在的条件下,设甲商品的日销售利润为w元,当甲商品的销售单价元件定为多少时,日销售利润最大?最大利润是多少?
为庆祝新中国成立70周年,国庆期间,北京举办“普天同庆共筑中国梦”的游园活动,为此,某公园在中央广场处建了一个人工喷泉,如图,人工喷泉有一个竖直的喷水枪AB,喷水口A距地面2m,喷出水流的运动路线是抛物线.如果水流的最高点P到喷水枪AB所在直线的距离为1m,且到地面的距离为,求水流的落地点C到水枪底部B的距离.
我市某乡镇实施产业精准扶贫,帮助贫困户承包了若干亩土地种植新品种草莓,已知该草莓的成本为每千克10元,草莓成熟后投入市场销售.经市场调查发现,草莓销售不会亏本,且每天的销售量千克与销售单价每千克元之间函数关系如图所示.
求y与x的函数关系式,并写出x的取值范围;
当该品种草莓的定价为多少时,每天销售获得利润最大?最大利润是多少?
某村今年草莓采摘期限30天,预计产量6000千克,若要求每天销售获得的利润最大,能否销售完这批草莓?请说明理由.
超市销售某种儿童玩具,如果每件利润为40元市场管理部门规定,该种玩具每件利润不能超过60元,每天可售出50件.根据市场调查发现,销售单价每增加2元,每天销售量会减少1件.设销售单价增加x元,每天售出y件.
请写出y与x之间的函数表达式;
设超市每天销售这种玩具可获利w元,当x为多少时w最大,最大值是多少?
某商品的进价为每件40元,在销售过程中发现,每周的销售量件与销售单价元之间的关系可以近似看作一次函数,且当售价定为50元件时,每周销售30件,当售价定为70元件时,每周销售10件.
求k,b的值;
求销售该商品每周的利润元与销售单价元之间的函数解析式,并求出销售该商品每周可获得的最大利润.
某山区不仅有美丽风光,也有许多令人喜爱的土特产,为实现脱贫奔小康,某村组织村民加工包装土特产销售给游客,以增加村民收入.已知某种土特产每袋成本10元.试销阶段每袋的销售价元与该土特产的日销售量袋之间的关系如表:
元
15
20
30
袋
25
20
10
若日销售量y是销售价x的一次函数,试求:
日销售量袋与销售价元的函数关系式;
假设后续销售情况与试销阶段效果相同,要使这种土特产每日销售的利润最大,每袋的销售价应定为多少元?每日销售的最大利润是多少元?
如图,开口向下的抛物线与x轴交于点、,与y轴交于点,点P是第一象限内抛物线上的一点.
求该抛物线所对应的函数解析式;
设四边形CABP的面积为S,求S的最大值.
某商场销售一批名牌衬衫,平均每天可售出20件.每件盈利120元.经调查发现,每件衬衫每降价10元,商场平均每天可多售出1件,为了扩大销售,减少库存,商场决定采取适当的降价措施.
若商场每天要盈利2070元,请你帮助商场算一算,每件衬衫应降价多少元?
这次降价活动中,2070元是最高日盈利吗?若是,请说明理由;若不是,试求最高盈利值.
青岛市某大酒店豪华间实行淡季、旺季两种价格标准,旺季每间价格比淡季上涨下表是去年该酒店豪华间某两天的相关记录:
?
淡季
旺季
未入住房间数
10
0
日总收入元
24000
40000
该酒店豪华间有多少间?旺季每间价格为多少元?
今年旺季来临,豪华间的间数不变.经市场调查发现,如果豪华间仍旧实行去年旺季价格,那么每天都客满;如果价格继续上涨,那么每增加25元,每天未入住房间数增加1间.不考虑其他因素,该酒店将豪华间的价格上涨多少元时,豪华间的日总收入最高?最高日总收入是多少元?
某广告公司设计一幅周长为16米的矩形广告牌,广告设计费为每平方米2000元.设矩形一边长为x,面积为S平方米.
求S与x之间的函数关系式,并写出自变量x的取值范围;
设计费能达到24000元吗?为什么?
当x是多少米时,设计费最多?最多是多少元?
毛泽东故居景区有一商店销售一种纪念品,这种商品的成本价为10元件,已知销售价不低于成本价,且物价部门规定这种商品的销售价不高于20元件,市场调查发现,该商品每天的销售量件与销售价元件之间的函数关系如图所示.
求y与x之间的函数关系式,并写出自变量x的取值范围
求每天的销售利润元与销售价元件之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大最大利润是多少
如图,抛物线与x轴交于A,B两点,其中点A在x轴的正半轴上,点B在x轴的负半轴上.
试写出该抛物线的对称轴和顶点C的坐标
在抛物线上是否存在一点M,使若存在,求出点M的坐标若不存在,请说明理由.
端午节前夕某超市调研一种进价为4元个的粽子的销售情况当每个售价为6元时,每天能卖出1400个,在此基础上售价每上涨元,每天销售量将减少10个根据物价局规定,售价不能超过进价的.
若要实现每天6000元的销售利润,售价应定为多少?
若按照物价局规定的最高售价,每天的利润会超过6000元吗?请说明理由.
某超市销售一种商品,每件成本为50元,销售人员经调查发现,销售单价为100元时,每月的销售量为50件,而销售单价每降低2元,则每月可多售出10件,且要求销售单价不得低于成本.
求该商品每月的销售量件与销售单价元之间的函数关系式;不需要求自变量取值范围
若使该商品每月的销售利润为4000元,并使顾客获得更多的实惠,销售单价应定为多少元?
超市的销售人员发现:当该商品每月销售量超过某一数量时,会出现所获利润反而减小的情况,为了每月所获利润最大,该商品销售单价应定为多少元?
新学期开始时,某校九年级一班的同学为了增添教室绿色文化,打造温馨舒适的学习环境,准备到一家植物种植基地购买A、B两种花苗.据了解,购买A种花苗3盆,B种花苗5盆,则需210元;购买A种花苗4盆,B种花苗10盆,则需380元.
求A、B两种花苗的单价分别是多少元?
经九年级一班班委会商定,决定购买A、B两种花苗共12盆进行搭配装扮教室.种植基地销售人员为了支持本次活动,为该班同学提供以下优惠:购买几盆B种花苗,B种花苗每盆就降价几元,请你为九年级一班的同学预算一下,本次购买至少准备多少钱?最多准备多少钱?
答案
1、【答案】解:由题意得,
.
由题意得,
解得?,,
当时,成本元元,不符合要求,舍去
当时,成本元元,符合要求,
售价应定为每件80元.
,,
当时,w取最大值,为9000,
故售价定为每件70元时会获得最大利润,最大利润为9000元.
2、【答案】解:根据题意得,
当时,w取得最大值,最大值为50.
当该商品的销售单价定为15元时,日销售利润最大,最大利润是50元.
3、【答案】解:设y与x之间的函数表达式为,
将、代入得
解得
与x之间的函数表达式为.
由题意得,
整理得,
解得,.
答:为保证某天获得600元的销售利润,则该天的销售价应定为60元千克或80元千克.
设当天的销售利润为w元,则,
,
当时,.
故销售价定为70元千克时,当天的销售利润最大,最大为800元.
4、【答案】解:设y与x之间的函数关系式为,
将、代入得解得
故.
由题意得,
,
有最大值,
当时,w有最大值,此时,,
故销售单价定为55元时,该商店每天获得的利润最大,最大利润为1250元.
由题意得,
解得,
故x的取值范围为.
5、【答案】解:设,
图象经过,
,
解得:,
表达式为.
6、【答案】解:设甲、乙两种商品的进货单价分别是a、b元件,由题意得:
,
解得:.
甲、乙两种商品的进货单价分别是10、15元件.
设y与x之间的函数关系式为,将,代入得:
,解得:.
与x之间的函数关系式为.
由题意得:
.
当时,w取得最大值50.
当甲商品的销售单价定为15元件时,日销售利润最大,最大利润是50元.
7、【答案】解:如图,以BD所在直线为x轴、AB所在直线为y轴建立直角坐标系,
由题意知,抛物线的顶点P的坐标为、点,
设抛物线的解析式为,
将点代入,得:,
解得:,
则抛物线的解析式为,
当时,有,
解得:舍或,
,
答:水流的落地点C到水枪底部B的距离为.
8、,
解得,
与x的函数关系式为;
由题意知,
.
设每天的销售利润为w元,
由题意知:
,
当时,w取最大值,为2025.
当该品种草莓定价为19元千克时,每天销售获得的利润最大,为2025元.
能销售完这批草莓.
当时,,
按照中的方式进行销售,能销售完这批草莓.
9、【答案】解:根据题意得,;
根据题意得,
,
,
当时,w随x的增大而增大,
该种玩具每件利润不能超过60元,的最大值为:,
当时,,
答:当x为20时w最大,最大值是2400元.
10、【答案】解:由题意可得:,
,
答:,;
,
当时,w有最大值为400元,
答:销售该商品每周可获得的最大利润为400元.
11、【答案】解:依题意,根据表格的数据,设日销售量袋与销售价元的函数关系式为得
,解得
故日销售量袋与销售价元的函数关系式为:
依题意,设利润为w元,得
整理得
当时,w取得最大值,最大值为225
故要使这种土特产每日销售的利润最大,每袋的销售价应定为25元,每日销售的最大利润是225元.
12、【答案】解:,,,
设抛物线表达式为:,
将C代入得:,
解得:,
该抛物线的解析式为:;
连接OP,设点P坐标为,,
,,,
可得:,,,
,
当时,S最大,最大值为8.
13、【答案】解:设每件衬衫应降价x元,由题意得:
,
解得:舍去,.
答:每件衬衫应降价30元.
这次降价活动中,2070元不是最高日盈利,理由如下:
设盈利为w元,由题意得:
,
,
当时,w取得最大值,此时.
即最高盈利是2400元.
14、【答案】解:设淡季每间的价格为x元,酒店豪华间有y间,
,
解得,,
,
答:该酒店豪华间有50间,旺季每间价格为800元;
设该酒店豪华间的价格上涨x元,日总收入为y元,
,
当时,y取得最大值,此时,
答:该酒店将豪华间的价格上涨225元时,豪华间的日总收入最高,最高日总收入是42025元.
15、【答案】解:矩形的一边为x米,周长为16米,
另一边长为米,
,其中;
能,
设计费能达到24000元,
当设计费为24000元时,面积为平方米,
即,
解得:或,
设计费能达到24000元.
,
当时,,
当米时,矩形的最大面积为16平方米,设计费最多,最多是32000元.
16、【答案】设函数解析式为:,根据题意,代入和得:
解得:
函数解析式为:.
根据题意得:
或,
该函数开口向下,
当时,W随x的增大而增大,
,当时,W有最大值,且最大值为200.
答:当每件售价为20元时,每天的销售利润最大,且最大利润是200元.
17、【答案】解:抛物线的对称轴是y轴,顶点C的坐标为.
不存在理由如下:
由已知条件易得点A的坐标为,点B的坐标为,
则,故是等腰直角三角形.
假设存在一点M,使,
因为AC为公共边,,
所以点M和点O关于直线AC对称,
因此四边形OAMC是正方形,所以点M的坐标为,
当时,,
所以点M不在抛物线上,
所以在抛物线上不存在一点M,使得.
18、【答案】解:设售价为x元,由题意得:
解得或
售价不能超过进价的.
,即
答:若要实现每天6000元的销售利润,售价应定为10元.
设售价为x元,利润为y元,由题意得
当时,函数能取得最大值,最大值为6400元.
答:按照物价局规定的最高售价,每天的利润会超过6000元,最大利润是6400元.
19、【答案】解:依题意,得:,
与x的函数关系式为;
依题意得:,
即,
解得:,,
,
当该商品每月销售利润为4000,为使顾客获得更多实惠,销售单价应定为70元;
设每月总利润为w,依题意得,
,此图象开口向下,
当时,w有最大值为4500元,
为了每月所获利润最大,该商品销售单价应定为80元.
20、【答案】解:设A、B两种花苗的单价分别是x元和y元,则,解得,
答:A、B两种花苗的单价分别是20元和30元;
设购买B花苗x盆,则购买A花苗为盆,设总费用为w元,
由题意得:,
故w有最大值,当时,w的最大值为265,当时,w的最小值为216,
故本次购买至少准备216元,最多准备265元.
某商店销售一种成本为每件40元的玩具,若按每件50元销售,一个月可售出500件,售价每涨1元,月销量就减少10件设售价为每件元,月销量为y件,月销售利润为w元.
写出y与x的函数解析式和w与x的函数解析式
商店要在月销售成本不超过10000元的情况下,使月销售利润达到8000元,售价应定为每件多少元
当售价定为每件多少元时会获得最大利润求出最大利润.
某超市购进一种商品,进货单价为10元,在销售过程中,超市规定,销售单价不低于10元且不高于19元如果该商品的销售单价单位:元与日销售量单位:件满足一次函数关系式,设该商品的日销售利润为w元,那么当该商品的销售单价单位:元定为多少时,日销售利润最大最大利润是多少元
某超市经销一种商品,每千克成本为50元经试销发现,该种商品每天的销售量千克与销售价元千克满足一次函数关系,其每天销售价、销售量的四组对应值如下表所示:
销售价元千克
55
60
65
70
销售量千克
70
60
50
40
求千克与元千克之间的函数表达式
为保证某天获得600元的销售利润,则该天的销售价应定为多少
当销售价定为多少时,才能使当天的销售利润最大最大利润是多少
某商店购进一批成本为每件30元的商品,经调查发现,该商品每天的销售量件与销售单价元之间满足一次函数关系,其图象如图所示.
求该商品每天的销售量件与销售单价元之间的函数关系式
销售单价定为多少时,才能使销售该商品每天获得的利润元最大最大利润是多少
若该商店想使销售该商品每天获得的利润不低于800元,请直接写出此时x的取值范围.
某次足球比赛,队员甲在前场给队友乙掷界外球.如图所示:已知两人相距8米,足球出手时的高度为米,运行的路线是抛物线,当足球运行的水平距离为2米时,足球达到最大高度4米.请你根据图中所建坐标系,求出抛物线的表达式.
黔东南州某超市购进甲、乙两种商品,已知购进3件甲商品和2件乙商品,需60元;购进2件甲商品和3件乙商品,需65元.
甲、乙两种商品的进货单价分别是多少?
设甲商品的销售单价为单位:元件,在销售过程中发现:当时,甲商品的日销售量单位:件与销售单价x之间存在一次函数关系,x、y之间的部分数值对应关系如表:
销售单价元件
11
19
日销售量件
18
2
请写出当时,y与x之间的函数关系式.
在的条件下,设甲商品的日销售利润为w元,当甲商品的销售单价元件定为多少时,日销售利润最大?最大利润是多少?
为庆祝新中国成立70周年,国庆期间,北京举办“普天同庆共筑中国梦”的游园活动,为此,某公园在中央广场处建了一个人工喷泉,如图,人工喷泉有一个竖直的喷水枪AB,喷水口A距地面2m,喷出水流的运动路线是抛物线.如果水流的最高点P到喷水枪AB所在直线的距离为1m,且到地面的距离为,求水流的落地点C到水枪底部B的距离.
我市某乡镇实施产业精准扶贫,帮助贫困户承包了若干亩土地种植新品种草莓,已知该草莓的成本为每千克10元,草莓成熟后投入市场销售.经市场调查发现,草莓销售不会亏本,且每天的销售量千克与销售单价每千克元之间函数关系如图所示.
求y与x的函数关系式,并写出x的取值范围;
当该品种草莓的定价为多少时,每天销售获得利润最大?最大利润是多少?
某村今年草莓采摘期限30天,预计产量6000千克,若要求每天销售获得的利润最大,能否销售完这批草莓?请说明理由.
超市销售某种儿童玩具,如果每件利润为40元市场管理部门规定,该种玩具每件利润不能超过60元,每天可售出50件.根据市场调查发现,销售单价每增加2元,每天销售量会减少1件.设销售单价增加x元,每天售出y件.
请写出y与x之间的函数表达式;
设超市每天销售这种玩具可获利w元,当x为多少时w最大,最大值是多少?
某商品的进价为每件40元,在销售过程中发现,每周的销售量件与销售单价元之间的关系可以近似看作一次函数,且当售价定为50元件时,每周销售30件,当售价定为70元件时,每周销售10件.
求k,b的值;
求销售该商品每周的利润元与销售单价元之间的函数解析式,并求出销售该商品每周可获得的最大利润.
某山区不仅有美丽风光,也有许多令人喜爱的土特产,为实现脱贫奔小康,某村组织村民加工包装土特产销售给游客,以增加村民收入.已知某种土特产每袋成本10元.试销阶段每袋的销售价元与该土特产的日销售量袋之间的关系如表:
元
15
20
30
袋
25
20
10
若日销售量y是销售价x的一次函数,试求:
日销售量袋与销售价元的函数关系式;
假设后续销售情况与试销阶段效果相同,要使这种土特产每日销售的利润最大,每袋的销售价应定为多少元?每日销售的最大利润是多少元?
如图,开口向下的抛物线与x轴交于点、,与y轴交于点,点P是第一象限内抛物线上的一点.
求该抛物线所对应的函数解析式;
设四边形CABP的面积为S,求S的最大值.
某商场销售一批名牌衬衫,平均每天可售出20件.每件盈利120元.经调查发现,每件衬衫每降价10元,商场平均每天可多售出1件,为了扩大销售,减少库存,商场决定采取适当的降价措施.
若商场每天要盈利2070元,请你帮助商场算一算,每件衬衫应降价多少元?
这次降价活动中,2070元是最高日盈利吗?若是,请说明理由;若不是,试求最高盈利值.
青岛市某大酒店豪华间实行淡季、旺季两种价格标准,旺季每间价格比淡季上涨下表是去年该酒店豪华间某两天的相关记录:
?
淡季
旺季
未入住房间数
10
0
日总收入元
24000
40000
该酒店豪华间有多少间?旺季每间价格为多少元?
今年旺季来临,豪华间的间数不变.经市场调查发现,如果豪华间仍旧实行去年旺季价格,那么每天都客满;如果价格继续上涨,那么每增加25元,每天未入住房间数增加1间.不考虑其他因素,该酒店将豪华间的价格上涨多少元时,豪华间的日总收入最高?最高日总收入是多少元?
某广告公司设计一幅周长为16米的矩形广告牌,广告设计费为每平方米2000元.设矩形一边长为x,面积为S平方米.
求S与x之间的函数关系式,并写出自变量x的取值范围;
设计费能达到24000元吗?为什么?
当x是多少米时,设计费最多?最多是多少元?
毛泽东故居景区有一商店销售一种纪念品,这种商品的成本价为10元件,已知销售价不低于成本价,且物价部门规定这种商品的销售价不高于20元件,市场调查发现,该商品每天的销售量件与销售价元件之间的函数关系如图所示.
求y与x之间的函数关系式,并写出自变量x的取值范围
求每天的销售利润元与销售价元件之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大最大利润是多少
如图,抛物线与x轴交于A,B两点,其中点A在x轴的正半轴上,点B在x轴的负半轴上.
试写出该抛物线的对称轴和顶点C的坐标
在抛物线上是否存在一点M,使若存在,求出点M的坐标若不存在,请说明理由.
端午节前夕某超市调研一种进价为4元个的粽子的销售情况当每个售价为6元时,每天能卖出1400个,在此基础上售价每上涨元,每天销售量将减少10个根据物价局规定,售价不能超过进价的.
若要实现每天6000元的销售利润,售价应定为多少?
若按照物价局规定的最高售价,每天的利润会超过6000元吗?请说明理由.
某超市销售一种商品,每件成本为50元,销售人员经调查发现,销售单价为100元时,每月的销售量为50件,而销售单价每降低2元,则每月可多售出10件,且要求销售单价不得低于成本.
求该商品每月的销售量件与销售单价元之间的函数关系式;不需要求自变量取值范围
若使该商品每月的销售利润为4000元,并使顾客获得更多的实惠,销售单价应定为多少元?
超市的销售人员发现:当该商品每月销售量超过某一数量时,会出现所获利润反而减小的情况,为了每月所获利润最大,该商品销售单价应定为多少元?
新学期开始时,某校九年级一班的同学为了增添教室绿色文化,打造温馨舒适的学习环境,准备到一家植物种植基地购买A、B两种花苗.据了解,购买A种花苗3盆,B种花苗5盆,则需210元;购买A种花苗4盆,B种花苗10盆,则需380元.
求A、B两种花苗的单价分别是多少元?
经九年级一班班委会商定,决定购买A、B两种花苗共12盆进行搭配装扮教室.种植基地销售人员为了支持本次活动,为该班同学提供以下优惠:购买几盆B种花苗,B种花苗每盆就降价几元,请你为九年级一班的同学预算一下,本次购买至少准备多少钱?最多准备多少钱?
答案
1、【答案】解:由题意得,
.
由题意得,
解得?,,
当时,成本元元,不符合要求,舍去
当时,成本元元,符合要求,
售价应定为每件80元.
,,
当时,w取最大值,为9000,
故售价定为每件70元时会获得最大利润,最大利润为9000元.
2、【答案】解:根据题意得,
当时,w取得最大值,最大值为50.
当该商品的销售单价定为15元时,日销售利润最大,最大利润是50元.
3、【答案】解:设y与x之间的函数表达式为,
将、代入得
解得
与x之间的函数表达式为.
由题意得,
整理得,
解得,.
答:为保证某天获得600元的销售利润,则该天的销售价应定为60元千克或80元千克.
设当天的销售利润为w元,则,
,
当时,.
故销售价定为70元千克时,当天的销售利润最大,最大为800元.
4、【答案】解:设y与x之间的函数关系式为,
将、代入得解得
故.
由题意得,
,
有最大值,
当时,w有最大值,此时,,
故销售单价定为55元时,该商店每天获得的利润最大,最大利润为1250元.
由题意得,
解得,
故x的取值范围为.
5、【答案】解:设,
图象经过,
,
解得:,
表达式为.
6、【答案】解:设甲、乙两种商品的进货单价分别是a、b元件,由题意得:
,
解得:.
甲、乙两种商品的进货单价分别是10、15元件.
设y与x之间的函数关系式为,将,代入得:
,解得:.
与x之间的函数关系式为.
由题意得:
.
当时,w取得最大值50.
当甲商品的销售单价定为15元件时,日销售利润最大,最大利润是50元.
7、【答案】解:如图,以BD所在直线为x轴、AB所在直线为y轴建立直角坐标系,
由题意知,抛物线的顶点P的坐标为、点,
设抛物线的解析式为,
将点代入,得:,
解得:,
则抛物线的解析式为,
当时,有,
解得:舍或,
,
答:水流的落地点C到水枪底部B的距离为.
8、,
解得,
与x的函数关系式为;
由题意知,
.
设每天的销售利润为w元,
由题意知:
,
当时,w取最大值,为2025.
当该品种草莓定价为19元千克时,每天销售获得的利润最大,为2025元.
能销售完这批草莓.
当时,,
按照中的方式进行销售,能销售完这批草莓.
9、【答案】解:根据题意得,;
根据题意得,
,
,
当时,w随x的增大而增大,
该种玩具每件利润不能超过60元,的最大值为:,
当时,,
答:当x为20时w最大,最大值是2400元.
10、【答案】解:由题意可得:,
,
答:,;
,
当时,w有最大值为400元,
答:销售该商品每周可获得的最大利润为400元.
11、【答案】解:依题意,根据表格的数据,设日销售量袋与销售价元的函数关系式为得
,解得
故日销售量袋与销售价元的函数关系式为:
依题意,设利润为w元,得
整理得
当时,w取得最大值,最大值为225
故要使这种土特产每日销售的利润最大,每袋的销售价应定为25元,每日销售的最大利润是225元.
12、【答案】解:,,,
设抛物线表达式为:,
将C代入得:,
解得:,
该抛物线的解析式为:;
连接OP,设点P坐标为,,
,,,
可得:,,,
,
当时,S最大,最大值为8.
13、【答案】解:设每件衬衫应降价x元,由题意得:
,
解得:舍去,.
答:每件衬衫应降价30元.
这次降价活动中,2070元不是最高日盈利,理由如下:
设盈利为w元,由题意得:
,
,
当时,w取得最大值,此时.
即最高盈利是2400元.
14、【答案】解:设淡季每间的价格为x元,酒店豪华间有y间,
,
解得,,
,
答:该酒店豪华间有50间,旺季每间价格为800元;
设该酒店豪华间的价格上涨x元,日总收入为y元,
,
当时,y取得最大值,此时,
答:该酒店将豪华间的价格上涨225元时,豪华间的日总收入最高,最高日总收入是42025元.
15、【答案】解:矩形的一边为x米,周长为16米,
另一边长为米,
,其中;
能,
设计费能达到24000元,
当设计费为24000元时,面积为平方米,
即,
解得:或,
设计费能达到24000元.
,
当时,,
当米时,矩形的最大面积为16平方米,设计费最多,最多是32000元.
16、【答案】设函数解析式为:,根据题意,代入和得:
解得:
函数解析式为:.
根据题意得:
或,
该函数开口向下,
当时,W随x的增大而增大,
,当时,W有最大值,且最大值为200.
答:当每件售价为20元时,每天的销售利润最大,且最大利润是200元.
17、【答案】解:抛物线的对称轴是y轴,顶点C的坐标为.
不存在理由如下:
由已知条件易得点A的坐标为,点B的坐标为,
则,故是等腰直角三角形.
假设存在一点M,使,
因为AC为公共边,,
所以点M和点O关于直线AC对称,
因此四边形OAMC是正方形,所以点M的坐标为,
当时,,
所以点M不在抛物线上,
所以在抛物线上不存在一点M,使得.
18、【答案】解:设售价为x元,由题意得:
解得或
售价不能超过进价的.
,即
答:若要实现每天6000元的销售利润,售价应定为10元.
设售价为x元,利润为y元,由题意得
当时,函数能取得最大值,最大值为6400元.
答:按照物价局规定的最高售价,每天的利润会超过6000元,最大利润是6400元.
19、【答案】解:依题意,得:,
与x的函数关系式为;
依题意得:,
即,
解得:,,
,
当该商品每月销售利润为4000,为使顾客获得更多实惠,销售单价应定为70元;
设每月总利润为w,依题意得,
,此图象开口向下,
当时,w有最大值为4500元,
为了每月所获利润最大,该商品销售单价应定为80元.
20、【答案】解:设A、B两种花苗的单价分别是x元和y元,则,解得,
答:A、B两种花苗的单价分别是20元和30元;
设购买B花苗x盆,则购买A花苗为盆,设总费用为w元,
由题意得:,
故w有最大值,当时,w的最大值为265,当时,w的最小值为216,
故本次购买至少准备216元,最多准备265元.
