2021-2022学年九年级数学沪科版上册22.2《相似三角形的判定》课时练习(word版含答案)
文档属性
| 名称 | 2021-2022学年九年级数学沪科版上册22.2《相似三角形的判定》课时练习(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 129.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-29 16:56:52 | ||
图片预览


文档简介
沪科版数学九年级上册
22.2《相似三角形的判定》课时练习
一、选择题
1.在Rt△ABC和Rt△DEF中,∠C=∠F=90°,下列条件中不能判定这两个三角形相似的是(
)
A.∠A=45°,∠D=45°
B.AC=9,BC=12,DF=6,EF=8
C.AC=3,BC=4,DF=6,DE=8
D.AB=10,AC=8,DE=15,EF=9
2.下列条件不能判定△ADB∽△ABC的是( )
A.∠ABD=∠ACB??
B.∠ADB=∠ABC???
C.AB2=AD?AC????
D.
=
3.如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,若BD=2AD,则(
)
A.=
B.=
C.=
D.=
4.如图,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE相似,还需满足下列条件中的(
)
A.=
B.=
C.=
D.=
5.如图所示,在?ABCD中,BE交AC,CD于G,F,交AD的延长线于E,则图中的相似三角形有(
)
A.3对
B.4对
C.5对
D.6对
6.如图,在大小为4×4的正方形网格中,是相似三角形的是(
)
A.①和②
B.②和③
C.①和③
D.②和④
7.已知一个三角形的两个内角分别是40°,60°,另一个三角形的两个内角分别是40°,80°,则这两个三角形(
)
A.一定不相似
B.不一定相似
C.一定相似
D.不能确定
8.如图,∠APD=90°,AP=PB=BC=CD,则下列结论成立的是(
)
A.△PAB∽△PCA
B.△PAB∽△PDA
C.△ABC∽△DBA
D.△ABC∽△DCA
二、填空题
9.如图,已知∠A=∠D,要使△ABC∽△DEF,还需添加一个条件,你添加的条件是 .(只需写一个条件,不添加辅助线和字母)
10.如图,若△ADE∽△ACB,且=,DE=10,则CB=
.
11.如图,在△ABC中,∠BAC=90°,∠B=30°,AD⊥BC,AE平分∠BAD,则△ABC∽ ,△BAD∽△ACD(写出一个三角形即可).
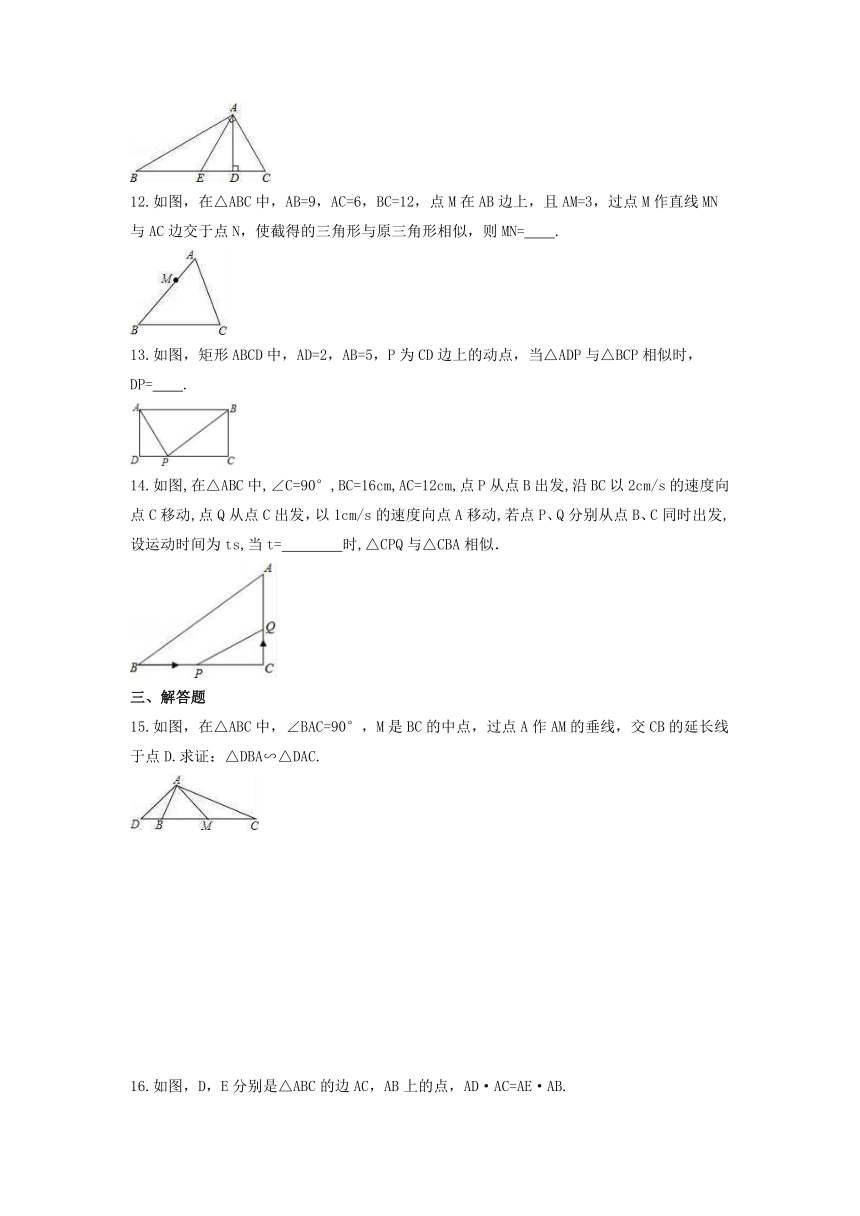
12.如图,在△ABC中,AB=9,AC=6,BC=12,点M在AB边上,且AM=3,过点M作直线MN与AC边交于点N,使截得的三角形与原三角形相似,则MN= .
13.如图,矩形ABCD中,AD=2,AB=5,P为CD边上的动点,当△ADP与△BCP相似时,DP= .
14.如图,在△ABC中,∠C=90°,BC=16cm,AC=12cm,点P从点B出发,沿BC以2cm/s的速度向点C移动,点Q从点C出发,以1cm/s的速度向点A移动,若点P、Q分别从点B、C同时出发,设运动时间为ts,当t=
时,△CPQ与△CBA相似.
三、解答题
15.如图,在△ABC中,∠BAC=90°,M是BC的中点,过点A作AM的垂线,交CB的延长线于点D.求证:△DBA∽△DAC.
16.如图,D,E分别是△ABC的边AC,AB上的点,AD·AC=AE·AB.
求证:△AED∽△ACB.
17.如图,点D,E分别为△ABC的边AC,AB上的点,BD,CE交于点O,且=,
试问△ADE与△ABC相似吗?请说明理由.
18.如图,已知∠DAB=∠EAC,∠ADE=∠ABC.求证:
(1)△ADE∽△ABC;
(2)=.
参考答案
1.答案为:C
2.答案为:D.
3.答案为:B
4.答案为:C
5.答案为:D
6.答案为:C
7.答案为:C
8.答案为:C
9.答案为:AB∥DE.
10.答案为:15
11.答案为:△DBA.
12.答案为:4或6.
13.答案为:1或4或2.5.
14.答案为4.8或.
15.证明:∵∠BAC=90°,点M是BC的中点,
∴AM=CM,
∴∠C=∠CAM,
∵DA⊥AM,
∴∠DAM=90°,
∴∠DAB=∠CAM,
∴∠DAB=∠C,
∵∠D=∠D,
∴△DBA∽△DAC.
16.解:
17.解:相似.理由如下:
因为=,∠BOE=∠COD,∠DOE=∠COB,
所以△BOE∽△COD,△DOE∽△COB.
所以∠EBO=∠DCO,∠DEO=∠CBO.
因为∠ADE=∠DCO+∠DEO,∠ABC=∠EBO+∠CBO,
所以∠ADE=∠ABC.
又因为∠A=∠A,
所以△ADE∽△ABC.
18.证明:(1)∵∠DAB=∠EAC,
∴∠DAB+∠BAE=∠EAC+∠BAE.
∴∠DAE=∠BAC.
又∵∠ADE=∠ABC,∴△ADE∽△ABC.
(2)∵△ADE∽△ABC,∴=.
∵∠DAB=∠EAC,
∴△ADB∽△AEC.∴=.
22.2《相似三角形的判定》课时练习
一、选择题
1.在Rt△ABC和Rt△DEF中,∠C=∠F=90°,下列条件中不能判定这两个三角形相似的是(
)
A.∠A=45°,∠D=45°
B.AC=9,BC=12,DF=6,EF=8
C.AC=3,BC=4,DF=6,DE=8
D.AB=10,AC=8,DE=15,EF=9
2.下列条件不能判定△ADB∽△ABC的是( )
A.∠ABD=∠ACB??
B.∠ADB=∠ABC???
C.AB2=AD?AC????
D.
=
3.如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,若BD=2AD,则(
)
A.=
B.=
C.=
D.=
4.如图,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE相似,还需满足下列条件中的(
)
A.=
B.=
C.=
D.=
5.如图所示,在?ABCD中,BE交AC,CD于G,F,交AD的延长线于E,则图中的相似三角形有(
)
A.3对
B.4对
C.5对
D.6对
6.如图,在大小为4×4的正方形网格中,是相似三角形的是(
)
A.①和②
B.②和③
C.①和③
D.②和④
7.已知一个三角形的两个内角分别是40°,60°,另一个三角形的两个内角分别是40°,80°,则这两个三角形(
)
A.一定不相似
B.不一定相似
C.一定相似
D.不能确定
8.如图,∠APD=90°,AP=PB=BC=CD,则下列结论成立的是(
)
A.△PAB∽△PCA
B.△PAB∽△PDA
C.△ABC∽△DBA
D.△ABC∽△DCA
二、填空题
9.如图,已知∠A=∠D,要使△ABC∽△DEF,还需添加一个条件,你添加的条件是 .(只需写一个条件,不添加辅助线和字母)
10.如图,若△ADE∽△ACB,且=,DE=10,则CB=
.
11.如图,在△ABC中,∠BAC=90°,∠B=30°,AD⊥BC,AE平分∠BAD,则△ABC∽ ,△BAD∽△ACD(写出一个三角形即可).
12.如图,在△ABC中,AB=9,AC=6,BC=12,点M在AB边上,且AM=3,过点M作直线MN与AC边交于点N,使截得的三角形与原三角形相似,则MN= .
13.如图,矩形ABCD中,AD=2,AB=5,P为CD边上的动点,当△ADP与△BCP相似时,DP= .
14.如图,在△ABC中,∠C=90°,BC=16cm,AC=12cm,点P从点B出发,沿BC以2cm/s的速度向点C移动,点Q从点C出发,以1cm/s的速度向点A移动,若点P、Q分别从点B、C同时出发,设运动时间为ts,当t=
时,△CPQ与△CBA相似.
三、解答题
15.如图,在△ABC中,∠BAC=90°,M是BC的中点,过点A作AM的垂线,交CB的延长线于点D.求证:△DBA∽△DAC.
16.如图,D,E分别是△ABC的边AC,AB上的点,AD·AC=AE·AB.
求证:△AED∽△ACB.
17.如图,点D,E分别为△ABC的边AC,AB上的点,BD,CE交于点O,且=,
试问△ADE与△ABC相似吗?请说明理由.
18.如图,已知∠DAB=∠EAC,∠ADE=∠ABC.求证:
(1)△ADE∽△ABC;
(2)=.
参考答案
1.答案为:C
2.答案为:D.
3.答案为:B
4.答案为:C
5.答案为:D
6.答案为:C
7.答案为:C
8.答案为:C
9.答案为:AB∥DE.
10.答案为:15
11.答案为:△DBA.
12.答案为:4或6.
13.答案为:1或4或2.5.
14.答案为4.8或.
15.证明:∵∠BAC=90°,点M是BC的中点,
∴AM=CM,
∴∠C=∠CAM,
∵DA⊥AM,
∴∠DAM=90°,
∴∠DAB=∠CAM,
∴∠DAB=∠C,
∵∠D=∠D,
∴△DBA∽△DAC.
16.解:
17.解:相似.理由如下:
因为=,∠BOE=∠COD,∠DOE=∠COB,
所以△BOE∽△COD,△DOE∽△COB.
所以∠EBO=∠DCO,∠DEO=∠CBO.
因为∠ADE=∠DCO+∠DEO,∠ABC=∠EBO+∠CBO,
所以∠ADE=∠ABC.
又因为∠A=∠A,
所以△ADE∽△ABC.
18.证明:(1)∵∠DAB=∠EAC,
∴∠DAB+∠BAE=∠EAC+∠BAE.
∴∠DAE=∠BAC.
又∵∠ADE=∠ABC,∴△ADE∽△ABC.
(2)∵△ADE∽△ABC,∴=.
∵∠DAB=∠EAC,
∴△ADB∽△AEC.∴=.
