2021-2022学年沪科版九年级数学上册22.2 相似三角形的判定 同步练习(word版含答案)
文档属性
| 名称 | 2021-2022学年沪科版九年级数学上册22.2 相似三角形的判定 同步练习(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 174.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-29 16:58:29 | ||
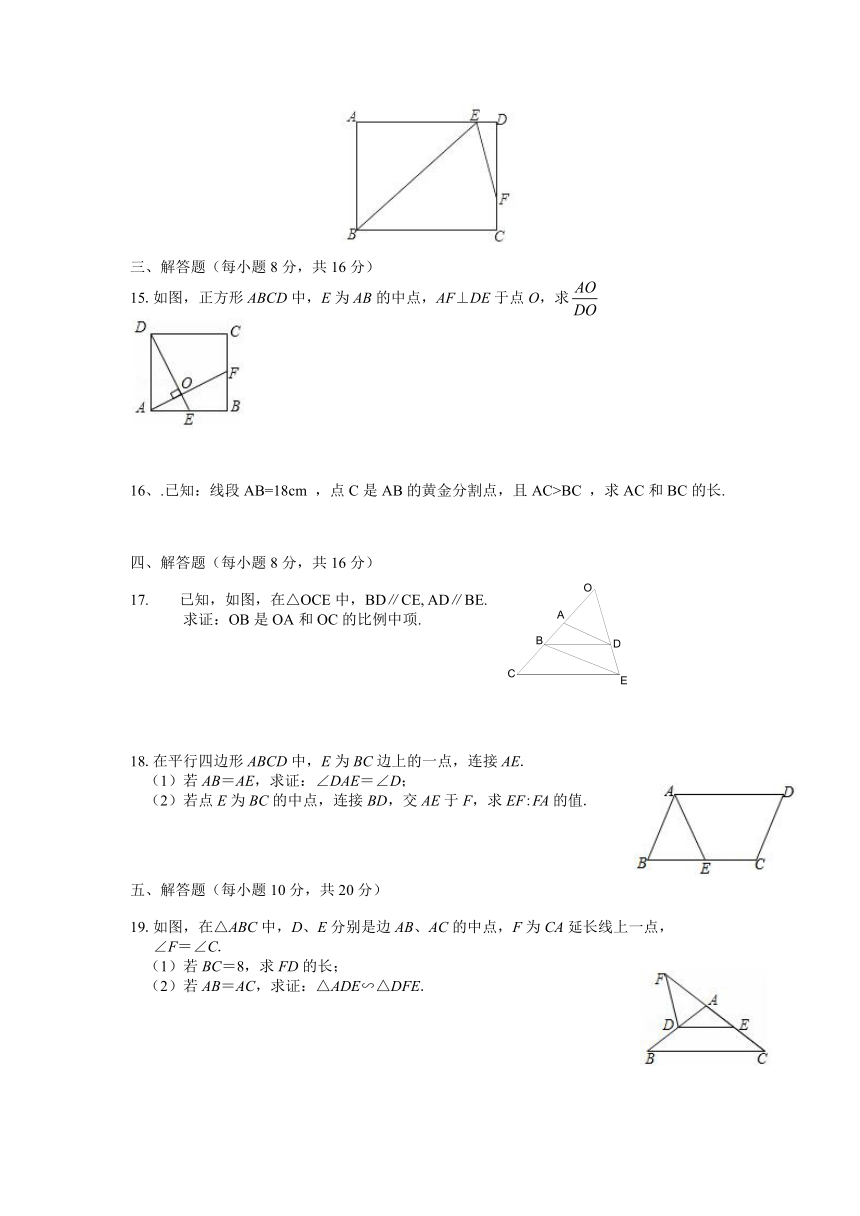
图片预览


文档简介
九年级数学(上)22.2相似三角形的判定练习题
一、选择题(每小题4分,共40分)
1﹒下列说法中,不正确的是(
)
A.直角边长分别是6、4和4.5、3的两个直角三角形相似
B.顶角为50°的两个等腰三角形相似
C.一个锐角为65°的两个直角三角形相似
D.有个角为30°的两个等腰三角形相似
2﹒如图,点P是平行四边形ABCD边AB上的一点,射线CP交DA的延长线于点E,则图中相似的三角形有(
)
A.0对
B.1对
C.2对
D.3对
3﹒如图,在△ABC中,点D、E分别在边AB、AC上,且DE不行于BC,则下列条件中不能判断△ABC∽△ADE的是(
)
A.∠AED=∠B
B.∠ADE=∠C
C.=
D.=
4﹒如图,在下列4×4的正方形(每个小正方形的边长都为1)网格中均有一个三角形,能相似的两个三角形是(
)
①
②
③
④
A.①和②
B.②和③
C.①和③
D.②和④
5﹒如图,在△ABC中,DE∥BC,=,AE=3,则BC的长为(
)
A.12
B.9
C.10
D.8
6﹒如图,在平行四边形ABCD中,点E是边AD上一点,且AE=2ED,EC交对角线BD于点F,则等于(
)
A.
B.
C.
D.
7﹒如图,在△ABC中,∠A=78°,AB=4,AC=6,将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
A. B.
C. D.
8﹒若△ABC的每条边长增加各自的20%得△A′B′C′,则∠B′的度数与其对应角∠B的度数相比( )
A.增加了20% B.减少了20% C.增加了(1+20%) D.没有改变
9﹒如图,△ABC中,E是BC中点,AD是∠BAC的平分线,EF∥AD交AC于F.若AB=11,AC=15,则FC的长为( )
A.11
B.12
C.13
D.14
10.如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,点E为AB的中点,给出下列结论:①CE∥AD;②AC2=ABAD;③△CDF∽△BCE;④AC:AF=DE:DF,其中正确的有(
)
A.①②
B.①②③
C.①②④
D.①②③④
二、填空题(每小题5分,共20分)
11.
已知,与相交于点.若,,则
.
12.如图,在边长为1的正方形网格中有点P、A、B、C,则图中所形成的三角形中,相似的三角形是______________________.
13.
如图,在△ABC纸板中,AC=4,BC=2,AB=5,P是AC上一点,过点P沿直线剪下一个与△ABC相似的小三角形纸板,如果有4种不同的剪法,那么AP长的取值范围是 .?
14、在矩形ABCD中,∠B的角平分线BE与AD交于点E,∠BED的角平分线EF与DC交于点F,若AB=9,DF=2FC,则BC=
.(结果保留根号)
三、解答题(每小题8分,共16分)
15.如图,正方形ABCD中,E为AB的中点,AF⊥DE于点O,求
16、.已知:线段AB=18cm
,点C是AB的黄金分割点,且AC>BC
,求AC和BC的长.
四、解答题(每小题8分,共16分)
17.
已知,如图,在△OCE中,BD∥CE,
AD∥BE.
求证:OB是OA和OC的比例中项.
18.在平行四边形ABCD中,E为BC边上的一点,连接AE.
(1)若AB=AE,求证:∠DAE=∠D;
(2)若点E为BC的中点,连接BD,交AE于F,求EF:FA的值.
五、解答题(每小题10分,共20分)
19.如图,在△ABC中,D、E分别是边AB、AC的中点,F为CA延长线上一点,
∠F=∠C.
(1)若BC=8,求FD的长;
(2)若AB=AC,求证:△ADE∽△DFE.
20.如图,在△ABC中,AB=AC,点P、D分别是BC、AC边上的点,且∠APD=∠B.
(1)求证:AC
:PC=BP:DC;
(2)若AB=10,BC=12,当PD∥AB时,求BP的长.
六、解答题(每小题12分)
21、如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.
(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
七、解答题(每小题12分)
22、块直角三角形木板的一条直角边AB长为1.5
m,斜边AC长为2.5
m,面积为1.5
m2,工人师傅要把它加工成一个面积最大的正方形桌面,请甲、乙两位同学进行设计加工方案,甲设计方案如图1,乙设计方案如图2.你认为哪位同学设计的方案较好?试说明理由.(加工损耗忽略不计,计算结果中可保留分数)
八、解答题(每小题14分)
23.如图,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿AB向点B以2cm/s的速度运动,点Q从点B开始沿BC向点C以4cm/s的速度运动.如果P、Q分别从A、B同时出发,4秒后停止运动,则在开始运动后第几秒,△BPQ与△BAC相似?
答案
一、D
D
C
B
B
;A
C
D
C
C
二、
11、4
12、△APB∽△CPA;
13、3≤AP<4
14、【答案】.
三、
15、∵∠ADO=∠ADO,∠DOA=∠DAE=90°,
∴△AOD∽△EAD,
∴,
16、AC=
9
5
-9
BC=27-9
5
17、在△OCE中,
∵BD∥CE.
在△OBE中,
∵AD∥BE.
即OB2=OA·OC.
∴OB是OA和OC的比例中项.
18、解答:(1)在平行四边形ABCD中,AD∥BC,
∴∠AEB=∠DAE,
∵AE=AB,
∴∠B=∠AEB,
∴∠B=∠DAE,
∵∠B=∠D,
∴∠DAE=∠D;
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴△BEF∽△AFD,
∴,
∵E为BC的中点,
∴BE=BC=AD,即,
∴EF:FA=1:2.
19、解答:(1)∵D、E分别是边AB、AC的中点,
∴DE=BC=4,DE∥BC.
∴∠AED=∠C.
∵∠F=∠C,
∴∠AED=∠F,
∴FD=DE=4;
(2)∵AB=AC,DE∥BC.
∴∠B=∠C=∠AED=∠ADE,
∵∠AED=∠F,
∴∠ADE=∠F,
又∵∠AED=∠AED,
∴△ADE∽△DFE.
20、解答:(1)∵AB=AC,∴∠B=∠C,
∵∠APD=∠B,∴∠APD=∠B=∠C,
∵∠APC=∠BAP+∠B,∠APC=∠APD+∠DPC,
∴∠BAP=∠DPC,
∴△ABP∽△PCD,∴AB
:PC=BP:DC;
∴AC
:PC=BP:DC;
(2)∵PD∥AB,∴∠APD=∠BAP.
∵∠APD=∠C,∴∠BAP=∠C.
∵∠B=∠B,
∴△BAP∽△BCA,∴.
∵AB=10,BC=12,∴,
∴BP=.
21、解答:(1)证明:∵四边形ABCD是正方形,
∴AB=AD,∠B=90°,AD∥BC,
∴∠AMB=∠EAF,
又∵EF⊥AM,
∴∠AFE=90°,
∴∠B=∠AFE,
∴△ABM∽△EFA;
(2)解:∵∠B=90°,AB=12,BM=5,
∴AM==13,AD=12,
∵F是AM的中点,∴AF=AM=6.5,
∵△ABM∽△EFA,∴,即,
∴AE=16.9,
∴DE=AE-AD=4.9.
22、解甲同学设计的方案较好,理由如下:
由AB=1.5m,S△ABC=1.5m2,可得BC=2m.
图1中,甲设计的正方形桌面边长为xm,
由DE∥AB,得Rt△CDE∽Rt△CBA.
所以,即.
所以3-1.5x=2x.解得x=.
图2中,乙设计的桌面的边长为ym,
由AC·BH=AB·BC,得BH=1.2m.
因为DE∥AC,所以Rt△BDE∽Rt△BAC.
所以.即.解得y=.
因为,所以x2>y2.
所以甲同学设计的方案较好.
23、解答:设在开始运动后第x秒,△BPQ与△BAC相似,
由题意得:AP=2xcm,PB=(8﹣2x)cm,BQ=4x,
分两种情况考虑:
当∠BPQ=∠C,∠B=∠B时,△PBQ∽△CBA,
∴,即,
解得:x=0.8,
当x=0.8秒时,△BPQ与△BAC相似;
当∠BPQ=∠A,∠B=∠B时,△BPQ∽△BAC,
∴,即,
解得:x=2,
当x=2秒时,△BPQ与△BAC相似.
综上,当x=0.8秒或2秒时,△BPQ与△BAC相似.
一、选择题(每小题4分,共40分)
1﹒下列说法中,不正确的是(
)
A.直角边长分别是6、4和4.5、3的两个直角三角形相似
B.顶角为50°的两个等腰三角形相似
C.一个锐角为65°的两个直角三角形相似
D.有个角为30°的两个等腰三角形相似
2﹒如图,点P是平行四边形ABCD边AB上的一点,射线CP交DA的延长线于点E,则图中相似的三角形有(
)
A.0对
B.1对
C.2对
D.3对
3﹒如图,在△ABC中,点D、E分别在边AB、AC上,且DE不行于BC,则下列条件中不能判断△ABC∽△ADE的是(
)
A.∠AED=∠B
B.∠ADE=∠C
C.=
D.=
4﹒如图,在下列4×4的正方形(每个小正方形的边长都为1)网格中均有一个三角形,能相似的两个三角形是(
)
①
②
③
④
A.①和②
B.②和③
C.①和③
D.②和④
5﹒如图,在△ABC中,DE∥BC,=,AE=3,则BC的长为(
)
A.12
B.9
C.10
D.8
6﹒如图,在平行四边形ABCD中,点E是边AD上一点,且AE=2ED,EC交对角线BD于点F,则等于(
)
A.
B.
C.
D.
7﹒如图,在△ABC中,∠A=78°,AB=4,AC=6,将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
A. B.
C. D.
8﹒若△ABC的每条边长增加各自的20%得△A′B′C′,则∠B′的度数与其对应角∠B的度数相比( )
A.增加了20% B.减少了20% C.增加了(1+20%) D.没有改变
9﹒如图,△ABC中,E是BC中点,AD是∠BAC的平分线,EF∥AD交AC于F.若AB=11,AC=15,则FC的长为( )
A.11
B.12
C.13
D.14
10.如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,点E为AB的中点,给出下列结论:①CE∥AD;②AC2=ABAD;③△CDF∽△BCE;④AC:AF=DE:DF,其中正确的有(
)
A.①②
B.①②③
C.①②④
D.①②③④
二、填空题(每小题5分,共20分)
11.
已知,与相交于点.若,,则
.
12.如图,在边长为1的正方形网格中有点P、A、B、C,则图中所形成的三角形中,相似的三角形是______________________.
13.
如图,在△ABC纸板中,AC=4,BC=2,AB=5,P是AC上一点,过点P沿直线剪下一个与△ABC相似的小三角形纸板,如果有4种不同的剪法,那么AP长的取值范围是 .?
14、在矩形ABCD中,∠B的角平分线BE与AD交于点E,∠BED的角平分线EF与DC交于点F,若AB=9,DF=2FC,则BC=
.(结果保留根号)
三、解答题(每小题8分,共16分)
15.如图,正方形ABCD中,E为AB的中点,AF⊥DE于点O,求
16、.已知:线段AB=18cm
,点C是AB的黄金分割点,且AC>BC
,求AC和BC的长.
四、解答题(每小题8分,共16分)
17.
已知,如图,在△OCE中,BD∥CE,
AD∥BE.
求证:OB是OA和OC的比例中项.
18.在平行四边形ABCD中,E为BC边上的一点,连接AE.
(1)若AB=AE,求证:∠DAE=∠D;
(2)若点E为BC的中点,连接BD,交AE于F,求EF:FA的值.
五、解答题(每小题10分,共20分)
19.如图,在△ABC中,D、E分别是边AB、AC的中点,F为CA延长线上一点,
∠F=∠C.
(1)若BC=8,求FD的长;
(2)若AB=AC,求证:△ADE∽△DFE.
20.如图,在△ABC中,AB=AC,点P、D分别是BC、AC边上的点,且∠APD=∠B.
(1)求证:AC
:PC=BP:DC;
(2)若AB=10,BC=12,当PD∥AB时,求BP的长.
六、解答题(每小题12分)
21、如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.
(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
七、解答题(每小题12分)
22、块直角三角形木板的一条直角边AB长为1.5
m,斜边AC长为2.5
m,面积为1.5
m2,工人师傅要把它加工成一个面积最大的正方形桌面,请甲、乙两位同学进行设计加工方案,甲设计方案如图1,乙设计方案如图2.你认为哪位同学设计的方案较好?试说明理由.(加工损耗忽略不计,计算结果中可保留分数)
八、解答题(每小题14分)
23.如图,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿AB向点B以2cm/s的速度运动,点Q从点B开始沿BC向点C以4cm/s的速度运动.如果P、Q分别从A、B同时出发,4秒后停止运动,则在开始运动后第几秒,△BPQ与△BAC相似?
答案
一、D
D
C
B
B
;A
C
D
C
C
二、
11、4
12、△APB∽△CPA;
13、3≤AP<4
14、【答案】.
三、
15、∵∠ADO=∠ADO,∠DOA=∠DAE=90°,
∴△AOD∽△EAD,
∴,
16、AC=
9
5
-9
BC=27-9
5
17、在△OCE中,
∵BD∥CE.
在△OBE中,
∵AD∥BE.
即OB2=OA·OC.
∴OB是OA和OC的比例中项.
18、解答:(1)在平行四边形ABCD中,AD∥BC,
∴∠AEB=∠DAE,
∵AE=AB,
∴∠B=∠AEB,
∴∠B=∠DAE,
∵∠B=∠D,
∴∠DAE=∠D;
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴△BEF∽△AFD,
∴,
∵E为BC的中点,
∴BE=BC=AD,即,
∴EF:FA=1:2.
19、解答:(1)∵D、E分别是边AB、AC的中点,
∴DE=BC=4,DE∥BC.
∴∠AED=∠C.
∵∠F=∠C,
∴∠AED=∠F,
∴FD=DE=4;
(2)∵AB=AC,DE∥BC.
∴∠B=∠C=∠AED=∠ADE,
∵∠AED=∠F,
∴∠ADE=∠F,
又∵∠AED=∠AED,
∴△ADE∽△DFE.
20、解答:(1)∵AB=AC,∴∠B=∠C,
∵∠APD=∠B,∴∠APD=∠B=∠C,
∵∠APC=∠BAP+∠B,∠APC=∠APD+∠DPC,
∴∠BAP=∠DPC,
∴△ABP∽△PCD,∴AB
:PC=BP:DC;
∴AC
:PC=BP:DC;
(2)∵PD∥AB,∴∠APD=∠BAP.
∵∠APD=∠C,∴∠BAP=∠C.
∵∠B=∠B,
∴△BAP∽△BCA,∴.
∵AB=10,BC=12,∴,
∴BP=.
21、解答:(1)证明:∵四边形ABCD是正方形,
∴AB=AD,∠B=90°,AD∥BC,
∴∠AMB=∠EAF,
又∵EF⊥AM,
∴∠AFE=90°,
∴∠B=∠AFE,
∴△ABM∽△EFA;
(2)解:∵∠B=90°,AB=12,BM=5,
∴AM==13,AD=12,
∵F是AM的中点,∴AF=AM=6.5,
∵△ABM∽△EFA,∴,即,
∴AE=16.9,
∴DE=AE-AD=4.9.
22、解甲同学设计的方案较好,理由如下:
由AB=1.5m,S△ABC=1.5m2,可得BC=2m.
图1中,甲设计的正方形桌面边长为xm,
由DE∥AB,得Rt△CDE∽Rt△CBA.
所以,即.
所以3-1.5x=2x.解得x=.
图2中,乙设计的桌面的边长为ym,
由AC·BH=AB·BC,得BH=1.2m.
因为DE∥AC,所以Rt△BDE∽Rt△BAC.
所以.即.解得y=.
因为,所以x2>y2.
所以甲同学设计的方案较好.
23、解答:设在开始运动后第x秒,△BPQ与△BAC相似,
由题意得:AP=2xcm,PB=(8﹣2x)cm,BQ=4x,
分两种情况考虑:
当∠BPQ=∠C,∠B=∠B时,△PBQ∽△CBA,
∴,即,
解得:x=0.8,
当x=0.8秒时,△BPQ与△BAC相似;
当∠BPQ=∠A,∠B=∠B时,△BPQ∽△BAC,
∴,即,
解得:x=2,
当x=2秒时,△BPQ与△BAC相似.
综上,当x=0.8秒或2秒时,△BPQ与△BAC相似.
