2021-2022学年沪科版九年级数学上册22.3 相似三角形的性质 课时练习(word版含答案)
文档属性
| 名称 | 2021-2022学年沪科版九年级数学上册22.3 相似三角形的性质 课时练习(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 261.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-29 16:59:28 | ||
图片预览

文档简介
沪科版数学九年级上册
22.3《相似三角形的性质》课时练习
一、选择题
1.如图所示,两个等边三角形,两个矩形,两个正方形,两个菱形各成一组,每组中的一个图形在另一个图形的内部,对应边平行,且对应边之间的距离都相等,那么两个图形不相似的一组是( )
A.
B.
C.
D.
2.两个相似多边形的一组对分别是3cm和4.5cm,如果它们的面积之和是78cm2,那么较大的多边形的面积是( )
A.44.8
B.42
C.52
D.54
3.用一个2倍放大镜照一个△ABC,下面说法中错误的是( )
A.△ABC放大后,是原来的2倍
B.△ABC放大后,各边长是原来的2倍
C.△ABC放大后,周长是原来的2倍
D.△ABC放大后,面积是原来的4倍
4.下列判断正确的是( )
A.所有的直角三角形都相似
B.所有的等腰直角三角形都相似
C.所有的菱形都相似
D.所有的矩形都相似
5.如图,在?ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF∶FC等于(
)
A.3∶2
B.3∶1
C.1∶1
D.1∶2
6.如图,E为矩形ABCD的CD边延长线上一点,BE交AD于G,AF⊥BE于F,图中相似三角形的对数是( )
A.5
B.7
C.8
D.10
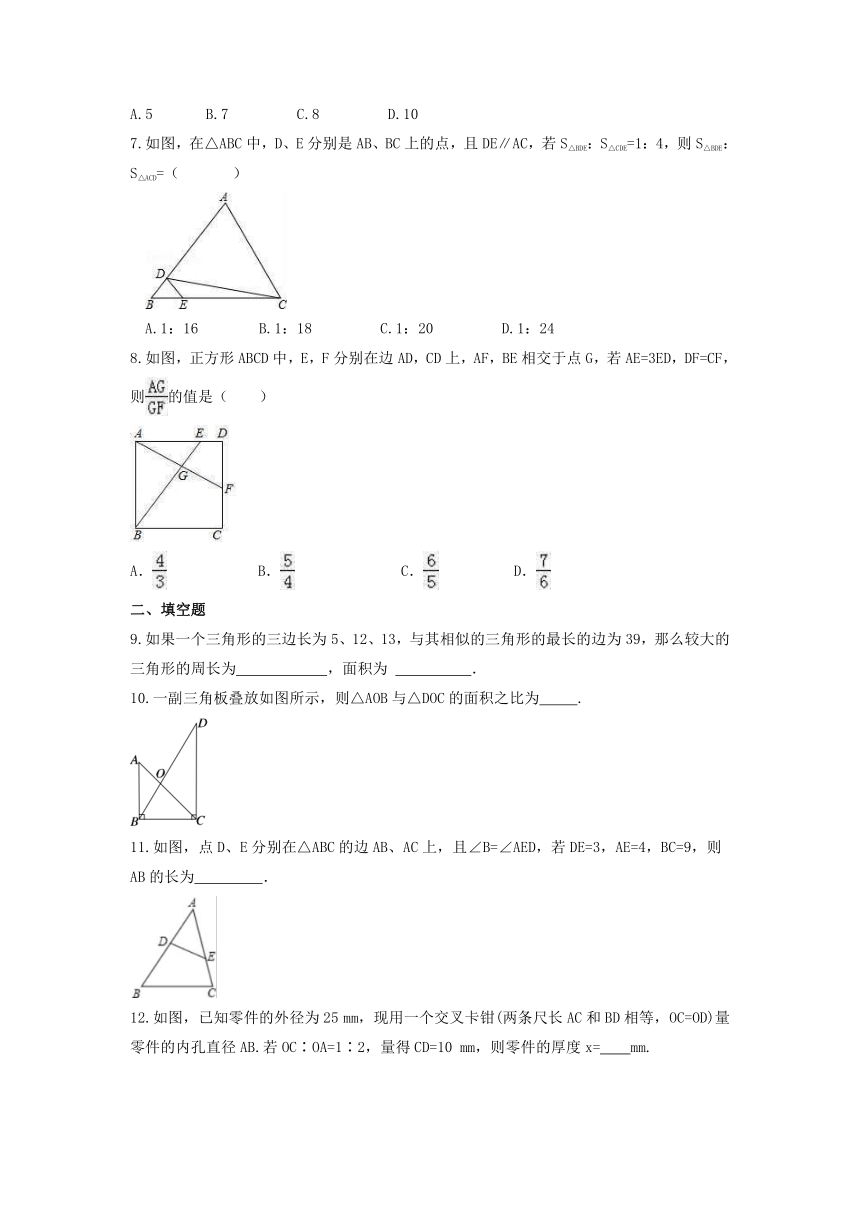
7.如图,在△ABC中,D、E分别是AB、BC上的点,且DE∥AC,若S△BDE:S△CDE=1:4,则S△BDE:S△ACD=(
)
A.1:16
B.1:18
C.1:20
D.1:24
8.如图,正方形ABCD中,E,F分别在边AD,CD上,AF,BE相交于点G,若AE=3ED,DF=CF,则的值是( )
A.??
???
B.????
??
C.???
?
D.
二、填空题
9.如果一个三角形的三边长为5、12、13,与其相似的三角形的最长的边为39,那么较大的三角形的周长为
,面积为
.
10.一副三角板叠放如图所示,则△AOB与△DOC的面积之比为
.
11.如图,点D、E分别在△ABC的边AB、AC上,且∠B=∠AED,若DE=3,AE=4,BC=9,则AB的长为
.
12.如图,已知零件的外径为25
mm,现用一个交叉卡钳(两条尺长AC和BD相等,OC=OD)量零件的内孔直径AB.若OC∶OA=1∶2,量得CD=10
mm,则零件的厚度x=
mm.
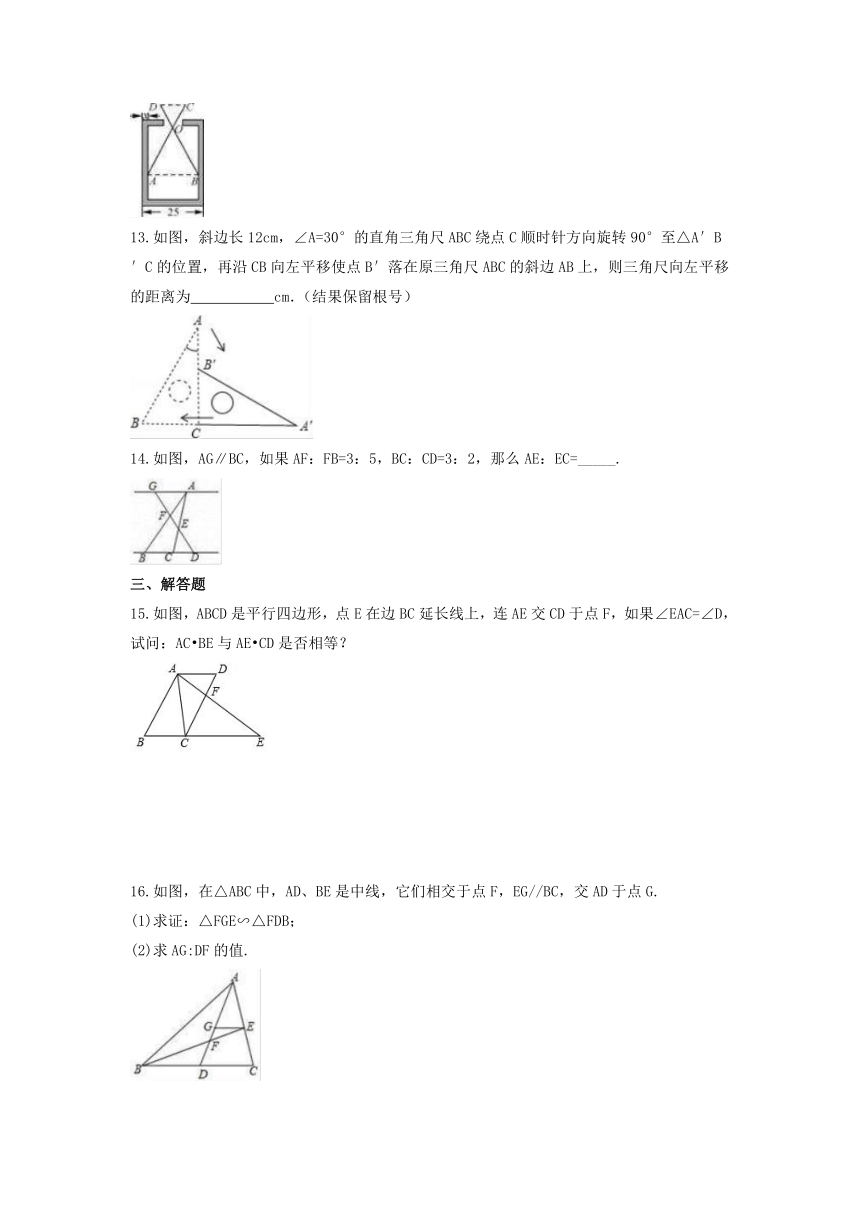
13.如图,斜边长12cm,∠A=30°的直角三角尺ABC绕点C顺时针方向旋转90°至△A′B′C的位置,再沿CB向左平移使点B′落在原三角尺ABC的斜边AB上,则三角尺向左平移的距离为
cm.(结果保留根号)
14.如图,AG∥BC,如果AF:FB=3:5,BC:CD=3:2,那么AE:EC=_____.
三、解答题
15.如图,ABCD是平行四边形,点E在边BC延长线上,连AE交CD于点F,如果∠EAC=∠D,
试问:AC?BE与AE?CD是否相等?
16.如图,在△ABC中,AD、BE是中线,它们相交于点F,EG//BC,交AD于点G.
(1)求证:△FGE∽△FDB;
(2)求AG:DF的值.
17.为了估计河的宽度,勘测人员在河的对岸选定一个目标点A,在近岸分别取点B、D、E、C,使点A、B、D在一条直线上,且AD⊥DE,点A、C、E也在一条直线上,且DE∥BC.经测量BC=24米,BD=12米,DE=40米,求河的宽度AB为多少米?
18.如图,在△ABC中,AB=AC,点P在BC上.
(1)求作:△PCD,使点D在AC上,且△PCD∽△ABP;(要求:尺规作图,保留作图痕迹,不写作法)
(2)在(1)的条件下,若∠APC=2∠ABC,求证:PD//AB.
参考答案
1.答案为:B
2.答案为:D
3.答案为:A
4.答案为:B
5.答案为:D.
6.答案为:D
7.答案为:C
8.答案为:C.
9.答案为:较大三角形的周长为90,面积为270.
10.答案为:1∶3
11.答案为:12.
12.答案为:2.5mm.
13.答案为:6﹣2.
14.答案为:3:2;
15.解:∵四边形ABCD是平行四边形,
∴∠D=∠B,
∵∠EAC=∠D,
∴∠EAC=∠B,
∵∠E=∠E,
∴△ACE∽△BAE,
∴AC:AE=AB:BE,
即AC?BE=AE?AB,
∵AB=CD,
∴AC?BE=AE?CD.
16.解:
17.解析
根据题意得出△ABE∽△CDE,进而利用相似三角形的性质得出答案.
解:设宽度AB为x米,
∵DE∥BC,∴△ABC∽△ADE,∴=,
又∵BC=24,BD=12,DE=40代入得∴=,解得x=18,
答:河的宽度为18米.
18.解:(1)∵△PCD∽△ABP,
∴∠CPD=∠BAP,
故作∠CPD=∠BAP即可,
如图,即为所作图形,
(2)∵∠APC=∠APD+∠DPC=∠ABC+∠BAP=2∠ABC,
∴∠BAP
=∠ABC,
∴∠BAP=∠CPD=∠ABC,
即∠CPD
=∠ABC,
∴PD∥AB.
22.3《相似三角形的性质》课时练习
一、选择题
1.如图所示,两个等边三角形,两个矩形,两个正方形,两个菱形各成一组,每组中的一个图形在另一个图形的内部,对应边平行,且对应边之间的距离都相等,那么两个图形不相似的一组是( )
A.
B.
C.
D.
2.两个相似多边形的一组对分别是3cm和4.5cm,如果它们的面积之和是78cm2,那么较大的多边形的面积是( )
A.44.8
B.42
C.52
D.54
3.用一个2倍放大镜照一个△ABC,下面说法中错误的是( )
A.△ABC放大后,是原来的2倍
B.△ABC放大后,各边长是原来的2倍
C.△ABC放大后,周长是原来的2倍
D.△ABC放大后,面积是原来的4倍
4.下列判断正确的是( )
A.所有的直角三角形都相似
B.所有的等腰直角三角形都相似
C.所有的菱形都相似
D.所有的矩形都相似
5.如图,在?ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF∶FC等于(
)
A.3∶2
B.3∶1
C.1∶1
D.1∶2
6.如图,E为矩形ABCD的CD边延长线上一点,BE交AD于G,AF⊥BE于F,图中相似三角形的对数是( )
A.5
B.7
C.8
D.10
7.如图,在△ABC中,D、E分别是AB、BC上的点,且DE∥AC,若S△BDE:S△CDE=1:4,则S△BDE:S△ACD=(
)
A.1:16
B.1:18
C.1:20
D.1:24
8.如图,正方形ABCD中,E,F分别在边AD,CD上,AF,BE相交于点G,若AE=3ED,DF=CF,则的值是( )
A.??
???
B.????
??
C.???
?
D.
二、填空题
9.如果一个三角形的三边长为5、12、13,与其相似的三角形的最长的边为39,那么较大的三角形的周长为
,面积为
.
10.一副三角板叠放如图所示,则△AOB与△DOC的面积之比为
.
11.如图,点D、E分别在△ABC的边AB、AC上,且∠B=∠AED,若DE=3,AE=4,BC=9,则AB的长为
.
12.如图,已知零件的外径为25
mm,现用一个交叉卡钳(两条尺长AC和BD相等,OC=OD)量零件的内孔直径AB.若OC∶OA=1∶2,量得CD=10
mm,则零件的厚度x=
mm.
13.如图,斜边长12cm,∠A=30°的直角三角尺ABC绕点C顺时针方向旋转90°至△A′B′C的位置,再沿CB向左平移使点B′落在原三角尺ABC的斜边AB上,则三角尺向左平移的距离为
cm.(结果保留根号)
14.如图,AG∥BC,如果AF:FB=3:5,BC:CD=3:2,那么AE:EC=_____.
三、解答题
15.如图,ABCD是平行四边形,点E在边BC延长线上,连AE交CD于点F,如果∠EAC=∠D,
试问:AC?BE与AE?CD是否相等?
16.如图,在△ABC中,AD、BE是中线,它们相交于点F,EG//BC,交AD于点G.
(1)求证:△FGE∽△FDB;
(2)求AG:DF的值.
17.为了估计河的宽度,勘测人员在河的对岸选定一个目标点A,在近岸分别取点B、D、E、C,使点A、B、D在一条直线上,且AD⊥DE,点A、C、E也在一条直线上,且DE∥BC.经测量BC=24米,BD=12米,DE=40米,求河的宽度AB为多少米?
18.如图,在△ABC中,AB=AC,点P在BC上.
(1)求作:△PCD,使点D在AC上,且△PCD∽△ABP;(要求:尺规作图,保留作图痕迹,不写作法)
(2)在(1)的条件下,若∠APC=2∠ABC,求证:PD//AB.
参考答案
1.答案为:B
2.答案为:D
3.答案为:A
4.答案为:B
5.答案为:D.
6.答案为:D
7.答案为:C
8.答案为:C.
9.答案为:较大三角形的周长为90,面积为270.
10.答案为:1∶3
11.答案为:12.
12.答案为:2.5mm.
13.答案为:6﹣2.
14.答案为:3:2;
15.解:∵四边形ABCD是平行四边形,
∴∠D=∠B,
∵∠EAC=∠D,
∴∠EAC=∠B,
∵∠E=∠E,
∴△ACE∽△BAE,
∴AC:AE=AB:BE,
即AC?BE=AE?AB,
∵AB=CD,
∴AC?BE=AE?CD.
16.解:
17.解析
根据题意得出△ABE∽△CDE,进而利用相似三角形的性质得出答案.
解:设宽度AB为x米,
∵DE∥BC,∴△ABC∽△ADE,∴=,
又∵BC=24,BD=12,DE=40代入得∴=,解得x=18,
答:河的宽度为18米.
18.解:(1)∵△PCD∽△ABP,
∴∠CPD=∠BAP,
故作∠CPD=∠BAP即可,
如图,即为所作图形,
(2)∵∠APC=∠APD+∠DPC=∠ABC+∠BAP=2∠ABC,
∴∠BAP
=∠ABC,
∴∠BAP=∠CPD=∠ABC,
即∠CPD
=∠ABC,
∴PD∥AB.
