2021-2022学年九年级数学沪科版上册22.4《图形的位似变换》课时练习(word版含答案)
文档属性
| 名称 | 2021-2022学年九年级数学沪科版上册22.4《图形的位似变换》课时练习(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 397.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-29 00:00:00 | ||
图片预览



文档简介
沪科版数学九年级上册
22.4《图形的位似变换》课时练习
一、选择题
1.下列说法不正确的是(
)
A.位似图形一定是相似图形
B.相似图形不一定是位似图形
C.位似图形上任意一对对应点到位似中心的距离之比等于位似比
D.位似图形中每组对应点所在的直线必相互平行
2.在下列图形中,不是位似图形的是(
??)
A.?
?B.??
?C.??
D.
3.如图,以点O为位似中心,将△ABC缩小后得到△A'B'C',已知OB=3OB',则△A'B'C'与△ABC的面积的比为(
)
A.1:3
B.1:4
C.1:5
D.1:9
4.如图,已知矩形ABCD和矩形EFGO在平面直角坐标系中,点B,F的坐标分别为(﹣4,4),(2,1).若矩形ABCD和矩形EFGO是位似图形,点P(点P在GC上)是位似中心,则点P的坐标为(
)
A.(0,3)
B.(0,2.5)
C.(0,2)
D.(0,1.5)
5.已知△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2),
以点B为位似中心,且位似比为1:2将△ABC放大得△A1BC1
,则点C1
的坐标为(
)
A.(1,0)
B.(5,8)
C.(4,6)或(5,8)
D.(1,0)或(5,8)
6.如图,线段CD两个端点的坐标分别为C(1,2)、D(2,0),以原点为位似中心,将线段CD放大得到线段AB,若点B坐标为(5,0),则点A的坐标为(
)
A.(2,5)
B.(2.5,5)
C.(3,5)
D.(3,6)
7.下列关于位似图形的表述:
①相似图形一定是位似图形,位似图形一定是相似图形;
②位似图形一定有位似中心;
③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么,这两个图形是位似图形;
④位似图形上任意两点与位似中心的距离之比等于位似比.
其中正确命题的序号是(
)
A.②
B.①②
C.③④
D.②③④
8.如图6×7的方格中,点A,B,C,D是格点,线段CD是由线段AB位似放大得到的,则它们的位似中心是( )
A.P1
B.P2
C.P3
D.P4
二、填空题
9.如图,线段CD两个端点的坐标分别为C(3,3),D(4,1),以原点O为位似中心,在第一象限内将线段CD扩大为原来的两倍,得到线段AB,则线段AB的中点E的坐标为
.
10.如图,在平面直角坐标系中,已知C(1,),△ABC与△DEF位似,原点O是位似中心,要使△DEF的面积是△ABC面积的5倍,则点F的坐标为
.
11.如图,在直角坐标系中,点E(﹣4,2),F(﹣2,﹣2),以O为位似中心,按2:1的相似比把△EFO缩小为△E′F′O,则点E的对应点E′的坐标为
.
12.如图,已知两点A(6,3),B(6,0),以原点O为位似中心,相似比为1:3把线段AB缩小,则点A的对应点坐标是___________.
13.如图,平面直角坐标系xOy中,点A、B的坐标分别为(3,0)、?
(2,﹣3),△AB′O′是△ABO关于的A的位似图形,且O′的坐标为(﹣1,0),则点B′的坐标为 ?????
.
14.如图,正方形OEFG和正方形ABCD是位似形,点F的坐标为(1,1),点C的坐标为(4,2),则这两个正方形位似中心的坐标是 .
三、作图题
15.小金鱼在直角坐标系中的位置如图所示,根据图形解答下面的问题:
(1)分别写出小金鱼身上点A、B、C、D、E、F的坐标;
(2)小金鱼身上的点的纵坐标都乘以﹣1,横坐标不变.作出相应图形,它与原图案有怎样的位置关系?
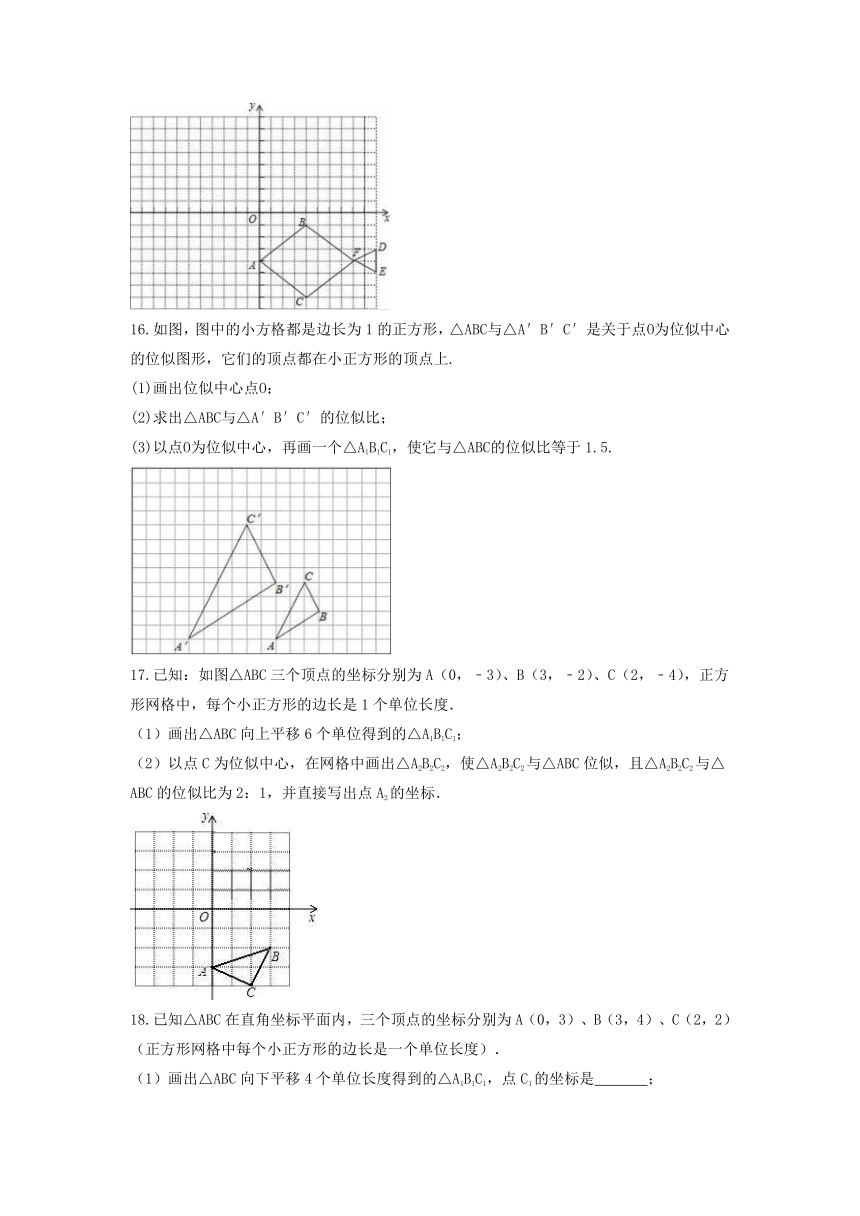
16.如图,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是关于点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
(1)画出位似中心点O;
(2)求出△ABC与△A′B′C′的位似比;
(3)以点O为位似中心,再画一个△A1B1C1,使它与△ABC的位似比等于1.5.
17.已知:如图△ABC三个顶点的坐标分别为A(0,﹣3)、B(3,﹣2)、C(2,﹣4),正方形网格中,每个小正方形的边长是1个单位长度.
(1)画出△ABC向上平移6个单位得到的△A1B1C1;
(2)以点C为位似中心,在网格中画出△A2B2C2,使△A2B2C2与△ABC位似,且△A2B2C2与△ABC的位似比为2:1,并直接写出点A2的坐标.
18.已知△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是
;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是
;
(3)△A2B2C2的面积是
平方单位.
参考答案
1.答案为:D;
2.答案为:D.
3.答案为:D;.
4.答案为:C;.
5.答案为:D;
6.答案为:B
7.答案为:A
8.答案为:C.
9.答案为:(7,4).
10.答案为:(,).
11.答案为:(2,﹣1)或(﹣2,1).
12.答案为:(2,1)或(﹣2,﹣1).
13.答案为:();?
14.答案为:(﹣2,0)或(,).
15.解:(1)如图所示:A(0,﹣4),B(4,0),C(4,﹣7),D(10,﹣3),
E(10,﹣5),F(8,﹣4);
(2)如图所示:它与原图案关于x轴对称.
16.解:(1)如图.
(2)△ABC与△A′B′C′的位似比为1:2.
(3)如图
17.解:(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:△A2B2C2,即为所求,A2坐标(﹣2,﹣2).
18.解:(1)如图所示:C1(2,﹣2);
故答案为:(2,﹣2);
(2)如图所示:C2(1,0);
故答案为:(1,0);
(3)∵A2C22=20,B2C2=20,A2B22=40,
∴△A2B2C2是等腰直角三角形,
∴△A2B2C2的面积是:×20=10平方单位.
故答案为:10.
22.4《图形的位似变换》课时练习
一、选择题
1.下列说法不正确的是(
)
A.位似图形一定是相似图形
B.相似图形不一定是位似图形
C.位似图形上任意一对对应点到位似中心的距离之比等于位似比
D.位似图形中每组对应点所在的直线必相互平行
2.在下列图形中,不是位似图形的是(
??)
A.?
?B.??
?C.??
D.
3.如图,以点O为位似中心,将△ABC缩小后得到△A'B'C',已知OB=3OB',则△A'B'C'与△ABC的面积的比为(
)
A.1:3
B.1:4
C.1:5
D.1:9
4.如图,已知矩形ABCD和矩形EFGO在平面直角坐标系中,点B,F的坐标分别为(﹣4,4),(2,1).若矩形ABCD和矩形EFGO是位似图形,点P(点P在GC上)是位似中心,则点P的坐标为(
)
A.(0,3)
B.(0,2.5)
C.(0,2)
D.(0,1.5)
5.已知△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2),
以点B为位似中心,且位似比为1:2将△ABC放大得△A1BC1
,则点C1
的坐标为(
)
A.(1,0)
B.(5,8)
C.(4,6)或(5,8)
D.(1,0)或(5,8)
6.如图,线段CD两个端点的坐标分别为C(1,2)、D(2,0),以原点为位似中心,将线段CD放大得到线段AB,若点B坐标为(5,0),则点A的坐标为(
)
A.(2,5)
B.(2.5,5)
C.(3,5)
D.(3,6)
7.下列关于位似图形的表述:
①相似图形一定是位似图形,位似图形一定是相似图形;
②位似图形一定有位似中心;
③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么,这两个图形是位似图形;
④位似图形上任意两点与位似中心的距离之比等于位似比.
其中正确命题的序号是(
)
A.②
B.①②
C.③④
D.②③④
8.如图6×7的方格中,点A,B,C,D是格点,线段CD是由线段AB位似放大得到的,则它们的位似中心是( )
A.P1
B.P2
C.P3
D.P4
二、填空题
9.如图,线段CD两个端点的坐标分别为C(3,3),D(4,1),以原点O为位似中心,在第一象限内将线段CD扩大为原来的两倍,得到线段AB,则线段AB的中点E的坐标为
.
10.如图,在平面直角坐标系中,已知C(1,),△ABC与△DEF位似,原点O是位似中心,要使△DEF的面积是△ABC面积的5倍,则点F的坐标为
.
11.如图,在直角坐标系中,点E(﹣4,2),F(﹣2,﹣2),以O为位似中心,按2:1的相似比把△EFO缩小为△E′F′O,则点E的对应点E′的坐标为
.
12.如图,已知两点A(6,3),B(6,0),以原点O为位似中心,相似比为1:3把线段AB缩小,则点A的对应点坐标是___________.
13.如图,平面直角坐标系xOy中,点A、B的坐标分别为(3,0)、?
(2,﹣3),△AB′O′是△ABO关于的A的位似图形,且O′的坐标为(﹣1,0),则点B′的坐标为 ?????
.
14.如图,正方形OEFG和正方形ABCD是位似形,点F的坐标为(1,1),点C的坐标为(4,2),则这两个正方形位似中心的坐标是 .
三、作图题
15.小金鱼在直角坐标系中的位置如图所示,根据图形解答下面的问题:
(1)分别写出小金鱼身上点A、B、C、D、E、F的坐标;
(2)小金鱼身上的点的纵坐标都乘以﹣1,横坐标不变.作出相应图形,它与原图案有怎样的位置关系?
16.如图,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是关于点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
(1)画出位似中心点O;
(2)求出△ABC与△A′B′C′的位似比;
(3)以点O为位似中心,再画一个△A1B1C1,使它与△ABC的位似比等于1.5.
17.已知:如图△ABC三个顶点的坐标分别为A(0,﹣3)、B(3,﹣2)、C(2,﹣4),正方形网格中,每个小正方形的边长是1个单位长度.
(1)画出△ABC向上平移6个单位得到的△A1B1C1;
(2)以点C为位似中心,在网格中画出△A2B2C2,使△A2B2C2与△ABC位似,且△A2B2C2与△ABC的位似比为2:1,并直接写出点A2的坐标.
18.已知△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是
;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是
;
(3)△A2B2C2的面积是
平方单位.
参考答案
1.答案为:D;
2.答案为:D.
3.答案为:D;.
4.答案为:C;.
5.答案为:D;
6.答案为:B
7.答案为:A
8.答案为:C.
9.答案为:(7,4).
10.答案为:(,).
11.答案为:(2,﹣1)或(﹣2,1).
12.答案为:(2,1)或(﹣2,﹣1).
13.答案为:();?
14.答案为:(﹣2,0)或(,).
15.解:(1)如图所示:A(0,﹣4),B(4,0),C(4,﹣7),D(10,﹣3),
E(10,﹣5),F(8,﹣4);
(2)如图所示:它与原图案关于x轴对称.
16.解:(1)如图.
(2)△ABC与△A′B′C′的位似比为1:2.
(3)如图
17.解:(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:△A2B2C2,即为所求,A2坐标(﹣2,﹣2).
18.解:(1)如图所示:C1(2,﹣2);
故答案为:(2,﹣2);
(2)如图所示:C2(1,0);
故答案为:(1,0);
(3)∵A2C22=20,B2C2=20,A2B22=40,
∴△A2B2C2是等腰直角三角形,
∴△A2B2C2的面积是:×20=10平方单位.
故答案为:10.
