2021-2022学年苏科版九年级数学上册《2.2圆的对称性》同步培优提升专题训练(word解析版)
文档属性
| 名称 | 2021-2022学年苏科版九年级数学上册《2.2圆的对称性》同步培优提升专题训练(word解析版) |
|
|
| 格式 | doc | ||
| 文件大小 | 547.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-28 00:00:00 | ||
图片预览

文档简介
2021年苏科版九年级数学上册《2.2圆的对称性》同步培优提升专题训练(附答案)
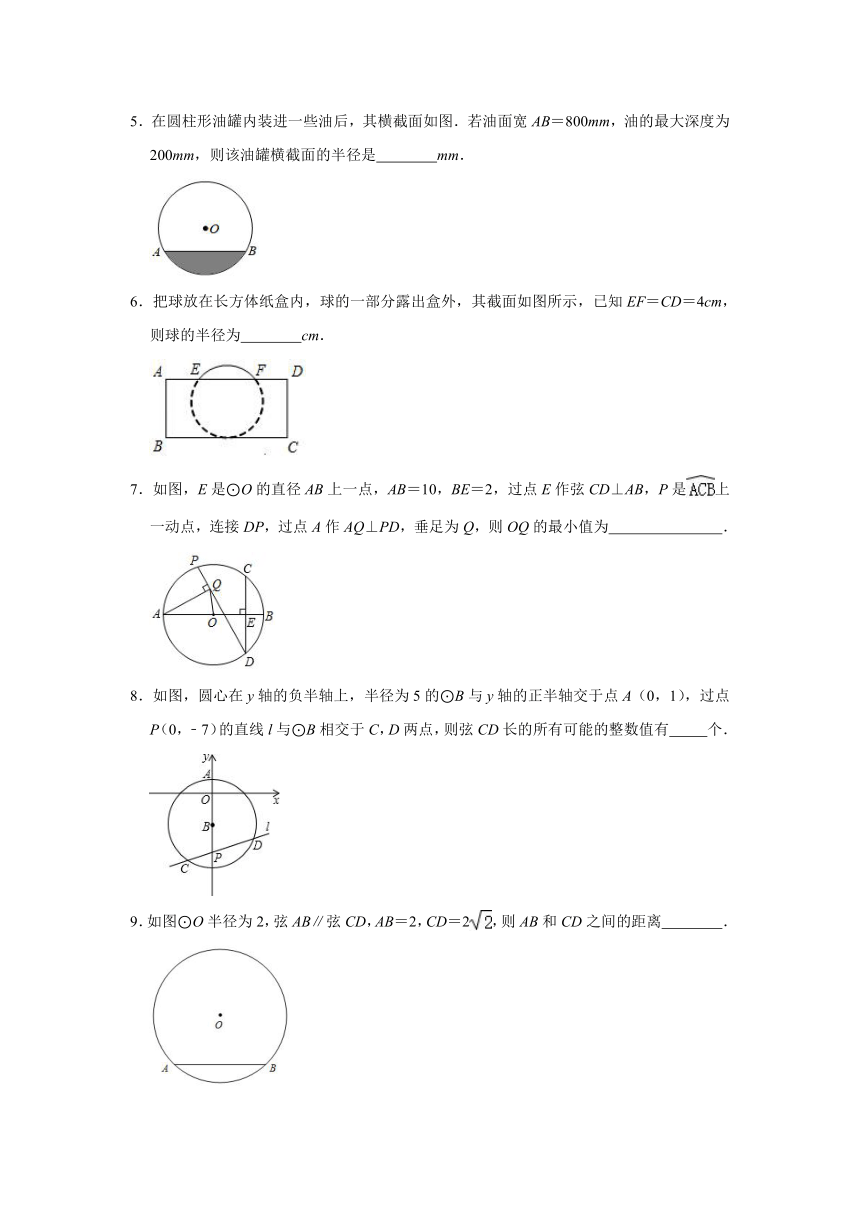
1.如图,在5×5正方形网格中,一条圆弧经过A、B、C三点,那么这条圆弧所在的圆的圆心为图中的( )
A.M
B.P
C.Q
D.R
2.已知AB是半径为1的圆O的一条弦,且AB=a<1,以AB为一边在圆O内作正△ABC,点D为圆O上不同于点A的一点,且DB=AB=a,DC的延长线交圆O于点E,则AE的长为( )
A.
B.1
C.
D.a
3.如图,在⊙O中,分别将、沿两条互相平行的弦AB、CD折叠,折叠后的弧均过圆心,若⊙O的半径为4,则四边形ABCD的面积是( )
A.8
B.16
C.32
D.32
4.如图,⊙O的半径OA=15,弦DE⊥AB于点C,若OC:BC=3:2,则DE的长为
.
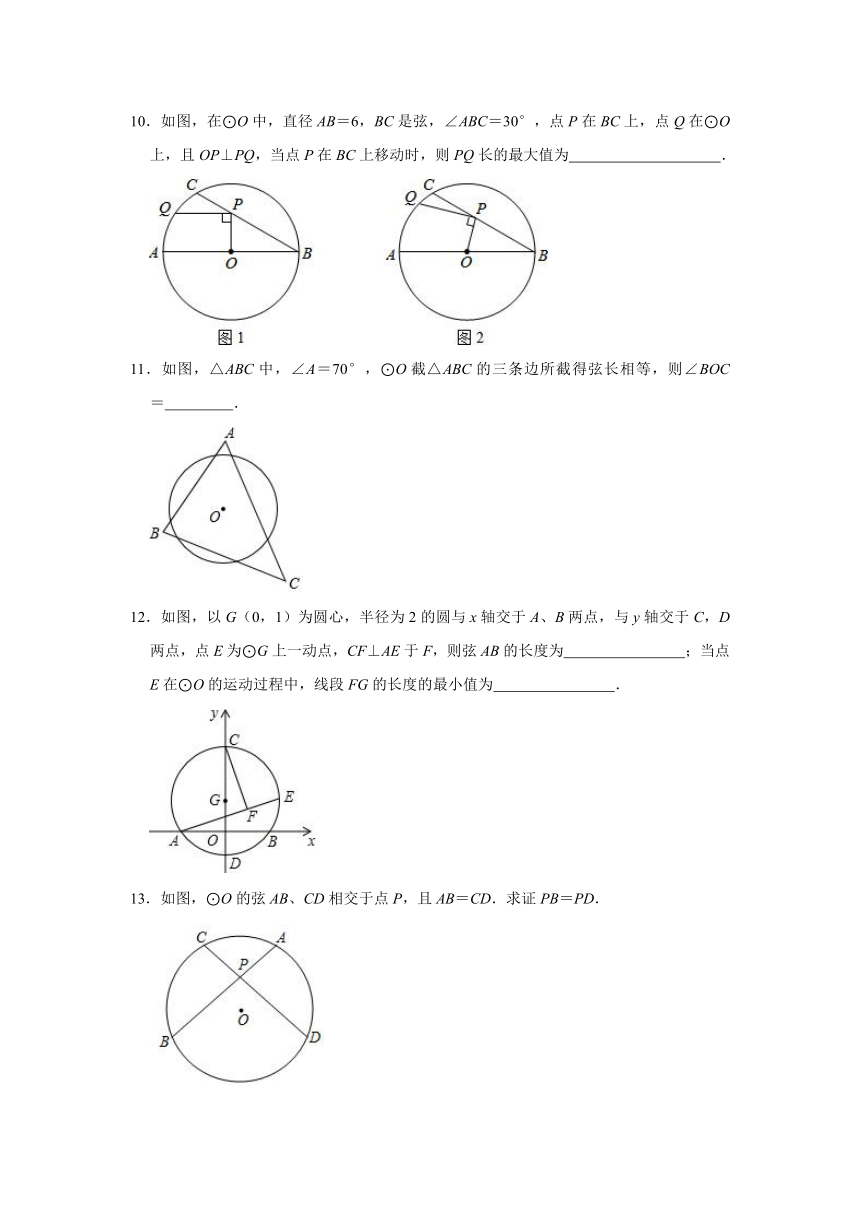
5.在圆柱形油罐内装进一些油后,其横截面如图.若油面宽AB=800mm,油的最大深度为200mm,则该油罐横截面的半径是
mm.
6.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=4cm,则球的半径为
cm.
7.如图,E是⊙O的直径AB上一点,AB=10,BE=2,过点E作弦CD⊥AB,P是上一动点,连接DP,过点A作AQ⊥PD,垂足为Q,则OQ的最小值为
.
8.如图,圆心在y轴的负半轴上,半径为5的⊙B与y轴的正半轴交于点A(0,1),过点P(0,﹣7)的直线l与⊙B相交于C,D两点,则弦CD长的所有可能的整数值有
个.
9.如图⊙O半径为2,弦AB∥弦CD,AB=2,CD=2,则AB和CD之间的距离
.
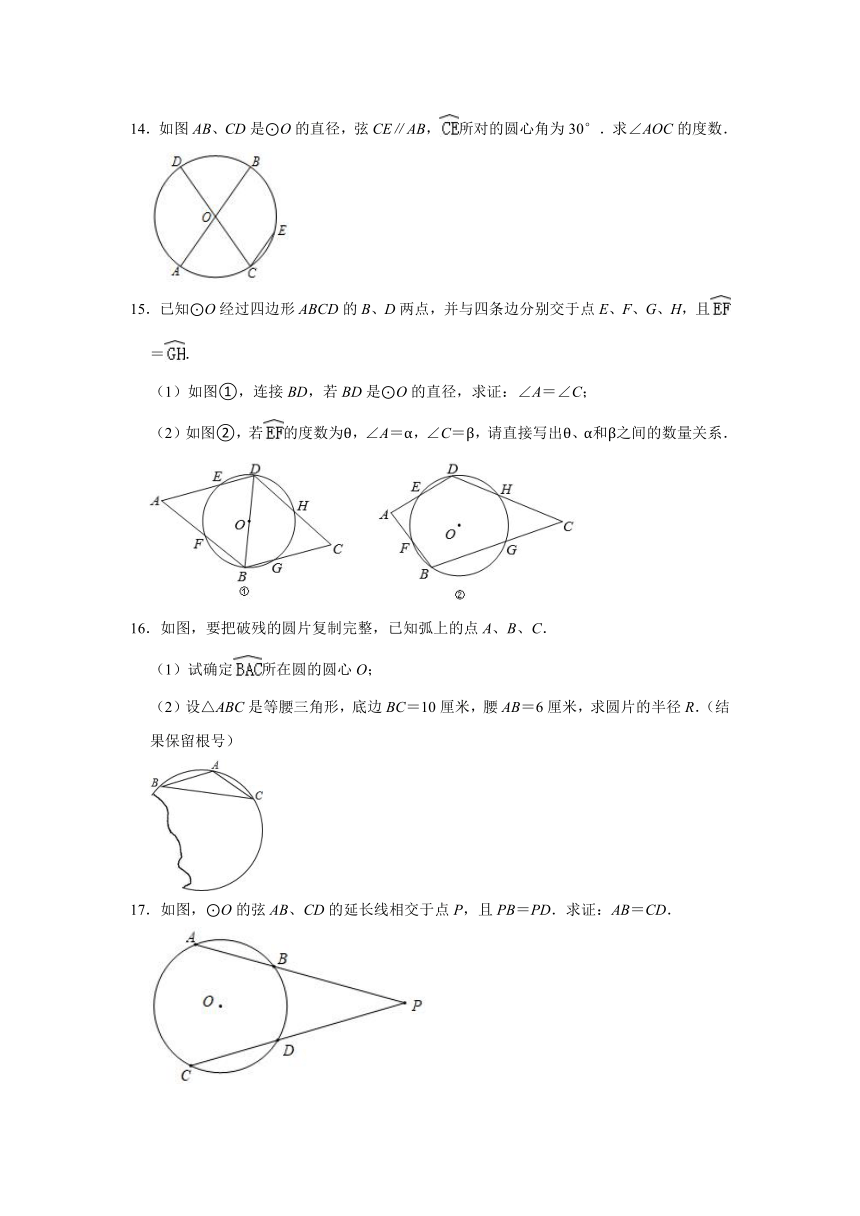
10.如图,在⊙O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP⊥PQ,当点P在BC上移动时,则PQ长的最大值为
.
11.如图,△ABC中,∠A=70°,⊙O截△ABC的三条边所截得弦长相等,则∠BOC=
.
12.如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C,D两点,点E为⊙G上一动点,CF⊥AE于F,则弦AB的长度为
;当点E在⊙O的运动过程中,线段FG的长度的最小值为
.
13.如图,⊙O的弦AB、CD相交于点P,且AB=CD.求证PB=PD.
14.如图AB、CD是⊙O的直径,弦CE∥AB,所对的圆心角为30°.求∠AOC的度数.
15.已知⊙O经过四边形ABCD的B、D两点,并与四条边分别交于点E、F、G、H,且=.
(1)如图①,连接BD,若BD是⊙O的直径,求证:∠A=∠C;
(2)如图②,若的度数为θ,∠A=α,∠C=β,请直接写出θ、α和β之间的数量关系.
16.如图,要把破残的圆片复制完整,已知弧上的点A、B、C.
(1)试确定所在圆的圆心O;
(2)设△ABC是等腰三角形,底边BC=10厘米,腰AB=6厘米,求圆片的半径R.(结果保留根号)
17.如图,⊙O的弦AB、CD的延长线相交于点P,且PB=PD.求证:AB=CD.
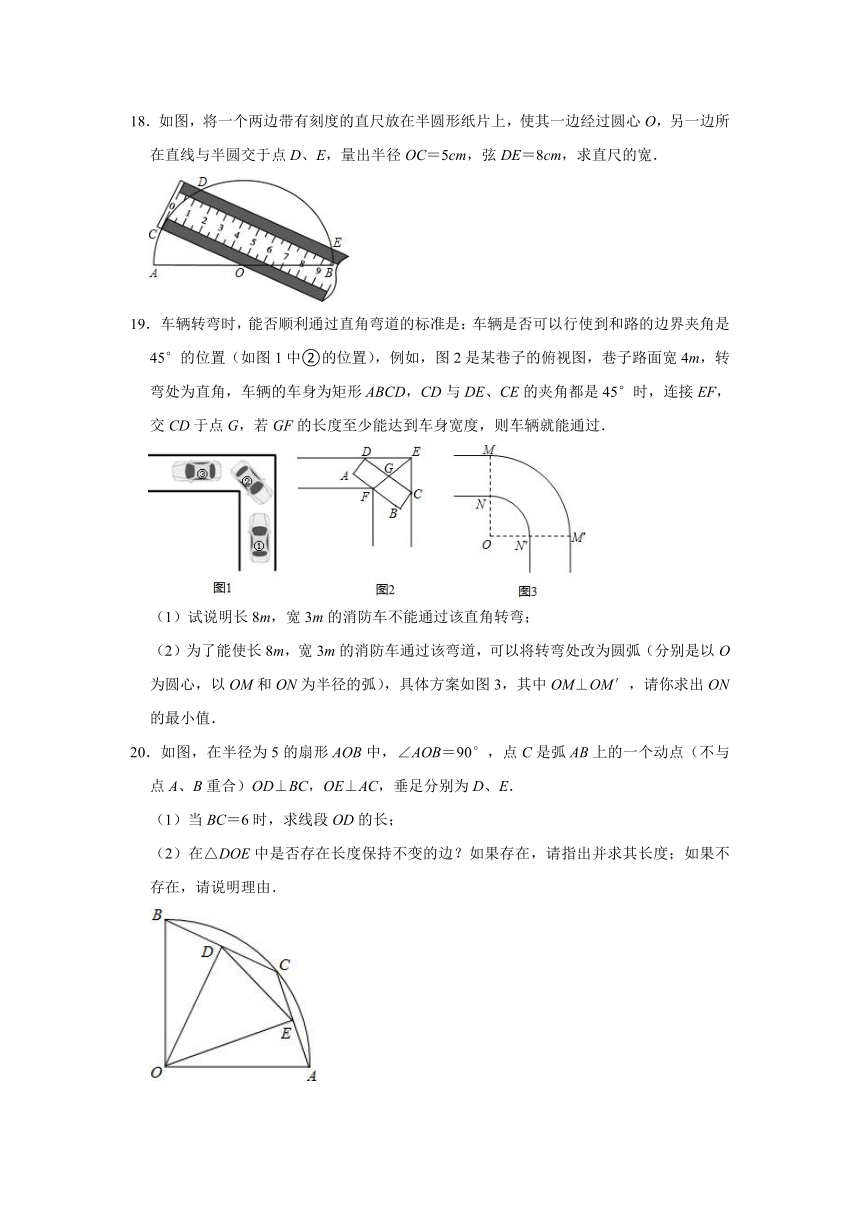
18.如图,将一个两边带有刻度的直尺放在半圆形纸片上,使其一边经过圆心O,另一边所在直线与半圆交于点D、E,量出半径OC=5cm,弦DE=8cm,求直尺的宽.
车辆转弯时,能否顺利通过直角弯道的标准是:车辆是否可以行使到和路的边界夹角是45°的位置(如图1中②的位置),例如,图2是某巷子的俯视图,巷子路面宽4m,转弯处为直角,车辆的车身为矩形ABCD,CD与DE、CE的夹角都是45°时,连接EF,交CD于点G,若GF的长度至少能达到车身宽度,则车辆就能通过.
(1)试说明长8m,宽3m的消防车不能通过该直角转弯;
(2)为了能使长8m,宽3m的消防车通过该弯道,可以将转弯处改为圆弧(分别是以O为圆心,以OM和ON为半径的弧),具体方案如图3,其中OM⊥OM′,请你求出ON的最小值.
20.如图,在半径为5的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E.
(1)当BC=6时,求线段OD的长;
(2)在△DOE中是否存在长度保持不变的边?如果存在,请指出并求其长度;如果不存在,请说明理由.
21.已知Rt△ABC中,∠ACB=90°,CA=CB,有一个圆心角为45°,半径的长等于CA的扇形CEF绕点C旋转,且直线CE,CF分别与直线AB交于点M,N.
(Ⅰ)当扇形CEF绕点C在∠ACB的内部旋转时,如图1,求证:MN2=AM2+BN2;
(思路点拨:考虑MN2=AM2+BN2符合勾股定理的形式,需转化为在直角三角形中解决.可将△ACM沿直线CE对折,得△DCM,连DN,只需证DN=BN,∠MDN=90°就可以了.请你完成证明过程.)
(Ⅱ)当扇形CEF绕点C旋转至图2的位置时,关系式MN2=AM2+BN2是否仍然成立?若成立,请证明;若不成立,请说明理由.
参考答案
1.解:作AB的垂直平分线,作BC的垂直平分线,如图,
它们都经过Q,所以点Q为这条圆弧所在圆的圆心.
故选:C.
2.解:∵△ABC是等边三角形,
∴AB=BC=AC=BD=a,∠CAB=∠ACB=60°;
∵AB=BD,
∴,
∴∠AED=∠AOB;
∵BC=AB=BD,
∴∠D=∠BCD;
∵四边形EABD内接于⊙O,
∴∠EAB+∠D=180°,即∠EAC+60°+∠D=180°;
又∵∠ECA+60°+∠BCD=180°,
∴∠ECA=∠EAC,即△EAC是等腰三角形;
在等腰△EAC和等腰△OAB中,∠AEC=∠AOB,
∵AC=AB,
∴△EAC≌△OAB;
∴AE=OA=1.
故选:B.
3.解:过O作OH⊥AB交⊙O于E,反向延长EO交CD于G,交⊙O于F,
连接OA,OB,OD,
∵AB∥CD,
∴EF⊥CD,
∵分别将、沿两条互相平行的弦AB、CD折叠,折叠后的弧均过圆心,
∴OH=OA,
∴∠HAO=30°,
∴∠AOH=60°,
同理∠DOG=60°,
∴∠AOD=60°,
∴△AOD是等边三角形,
∵OA=OB,
∴∠ABO=∠BAO=30°,
∴∠AOB=120°,
∴∠AOD+∠AOB=180°,
∴D,O,B三点共线,且BD为⊙O的直径,
∴∠DAB=90°,
同理,∠ABC=∠ADC=90°,
∴四边形ABCD是矩形,
∴AD=AO=4,AB=AD=4,
∴四边形ABCD的面积是16,
故选:B.
4.解:连接OD.
∵OA=OB=15,OC:BC=3:2,
∴BC=6,OC=9,
∵AB⊥DE,
∴CD=CE===12,
∴DE=2CD=24,
故答案为:24.
5.解:过O作OD⊥AB于C,交圆O于D,连接OA,如图所示:
则AC=BC=AB=400(mm),CD=200mm,
设该油罐横截面的半径为xmm,则OC=(x﹣200)mm,
在Rt△AOC中,由勾股定理得:4002+(x﹣200)2=x2,
解得:x=500,
即该油罐横截面的半径为500mm,
故答案为:500.
6.解:EF的中点M,作MN⊥AD于点M,取MN上的球心O,连接OF,
∵四边形ABCD是矩形,
∴∠C=∠D=90°,
∴四边形CDMN是矩形,
∴MN=CD=4,
设OF=x,则ON=OF,
∴OM=MN﹣ON=4﹣x,MF=2,
在直角三角形OMF中,OM2+MF2=OF2
即:(4﹣x)2+22=x2
解得:x=2.5
故答案为:2.5
7.解:∵AQ⊥PD,垂足为Q,
∴∠AQD=90°,
∴点Q在以AD为直径的圆上,
连接AD,以AD为直径作⊙M,如图,
连接MO并延长交⊙M于Q′,
当Q点运动到Q′时,OQ的值最小,
连接OD,
在Rt△ODE中,∵OD=5,OE=5﹣2=3,
∴DE==4,
在Rt△ADE中,AD==4,
∴MA=MQ′=2,
在Rt△AOM中,OM==,
∴OQ′=MQ′﹣OM=2﹣=,
∴OQ的最小值为.
故答案为.
8.解:∵点A的坐标为(0,1),圆的半径为5,
∴点B的坐标为(0,﹣4),
又∵点P的坐标为(0,﹣7),
∴BP=3,
①当CD垂直圆的直径AE时,CD的值最小,
连接BC,
在Rt△BCP中,CP==4;
故CD=2CP=8,
②当CD经过圆心时,CD的值最大,此时CD=直径AE=10;
所以,8≤CD≤10,
所以符合的弦有4条,整数值是8(一条弦),9(两条弦),10(一条弦),
综上可得:弦CD长的所有可能的整数值有:8,9,10,共3个,
故答案为:3.
9.解:①当弦AB和CD在圆心同侧时,如图1所示,
∵AB=2,CD=2,
∴AF=1,CE=,
∵OA=OC=2,
∴EO===,OF==,
∴EF=OF﹣OE=﹣;
②当弦AB和CD在圆心异侧时,如图2所示,
∵AB=2,CD=2,
∴AE=1,CF=,
∵OA=OC=2,
同法可得EO=,OF=,
∴EF=OF+OE=+;
综上所述:AB和CD之间的距离为﹣或+.
故答案为:﹣或+.
10.解:如图2中连接OQ,∵PQ=,OQ为定值,
∴当OP⊥BC时,OP的值最小,此时PQ长的最大.
此时OP=OB=,
在Rt△OPQ中,PQ==.
故答案为.
11.解:过O作OM⊥AB于M,ON⊥BC于N,OQ⊥AC于Q,连接OK、OD、OF、OB、OC,设AB,AC,BC与⊙O的另一个交点分别为E,H,G.
由垂径定理得:DM=DE,KQ=KH,FN=FG,
∵DE=FG=HK,
∴DM=KQ=FN,
∵OD=OK=OF,
∴由勾股定理得:OM=ON=OQ,
即O到三角形ABC三边的距离相等,
∴O是△ABC的内心,
∴∠OBC+∠OCB=(180°﹣70°)=55°,
∴∠BOC=125°,
故答案为125°.
12.解:作GM⊥AC于M,连接AG.
∵GO⊥AB,
∴OA=OB,
在Rt△AGO中,∵AG=2,OG=1,
∴AG=2OG,OA==,
∴∠GAO=30°,AB=2AO=2,
∴∠AGO=60°,
∵GC=GA,
∴∠GCA=∠GAC,
∵∠AGO=∠GCA+∠GAC,
∴∠GCA=∠GAC=30°,
∴AC=2OA=2,MG=CG=1,
∵∠AFC=90°,
∴点F在以AC为直径的⊙M上,
当点F在MG的延长线上时,FG的长最小,最小值=FM﹣GM=﹣1.
故答案为2,﹣1.
13.证明:连接BD.
∵AB=CD,
∴=
∴﹣=﹣,即=,
∴∠B=∠D,
∴PB=PD.
14.解:连接OE,如图,
∵为30°,
∴∠COE=30°,
∵OC=OE,
∴∠OCE=∠OEC,
∴∠OCE=(180°﹣30°)÷2=75°,
∵弦CE∥AB,
∴∠AOC=∠OCE=75°.
15.解:(1)连接DF、DG.
∵BD是⊙O的直径,
∴∠DFB=∠DGB=90°,
∵=,
∴∠EDF=∠HDG,
∵∠DFB=∠EDF+∠A,
∠DGB=∠HDG+∠C,
∴∠A=∠C.
(2)结论:α+β+θ=180°.
理由:如图②中,连接DF,BH.
∵=,
∴∠ADF=∠HBG=θ,
∵∠AFD+∠DFB=180°,∠DFB+∠DHB=180°,
∴∠AFD=∠DHB,
∵∠A+∠ADF+∠AFD=180°,∠AFD=∠DHB=∠C+∠HBG,
∴∠A+θ+∠C+θ=180°,
∴α+β+θ=180°.
16.解:(1)作DO⊥AB.DO必过圆心,作EO⊥AC,EO必过圆心,DO、EO交点必为圆心;
(2)
设半径为r.连接OA,因为BA=AC,故AO⊥BC.
所以:CD=×10=5,AD==.
根据勾股定理,(R﹣)2+52=R2,解得R=.
17.证明:如图,连接BD
∵PB=PD
∴∠PBD=∠PDB,
∴优弧=优弧,
∴﹣=﹣,即=,
∴AB=CD.
18.解:过点O作OM⊥DE于点M,连接OD.
∴DM=DE.
∵DE=8(cm)
∴DM=4(cm)
在Rt△ODM中,∵OD=OC=5(cm),
∴OM===3(cm)
∴直尺的宽度为3cm.
19.解:(1)消防车不能通过该直角转弯.
理由如下:如图,作FH⊥EC,垂足为H,
∵FH=EH=4,
∴EF=4,且∠GEC=45°,
∵GC=4,
∴GE=GC=4,
∴GF=4﹣4<3,
即GF的长度未达到车身宽度,
∴消防车不能通过该直角转弯;
(2)若C、D分别与M′、M重合,则△OGM为等腰直角三角形,
∴OG=4,OM=4,
∴OF=ON=OM﹣MN=4﹣4,
∴FG=OG﹣OF=×8﹣(4﹣4)=8﹣4<3,
∴C、D在上,
设ON=x,连接OC,在Rt△OCG中,
OG=x+3,OC=x+4,CG=4,
由勾股定理得,OG2+CG2=OC2,
即(x+3)2+42=(x+4)2,
解得x=4.5.
答:ON至少为4.5米.
20.解:(1)如图(1),
∵OD⊥BC,
∴BD=BC=×6=3,
∵∠BDO=90°,OB=5,BD=3,
∴OD==4,
即线段OD的长为4.
(2)存在,DE保持不变.
理由:连接AB,如图(2),
∵∠AOB=90°,OA=OB=5,
∴AB==5,
∵OD⊥BC,OE⊥AC,
∴D和E分别是线段BC和AC的中点,
∴DE=AB=,
∴DE保持不变.
21.(Ⅰ)证明:∵将△ACM沿直线CE对折,得△DCM,连DN,
∴△DCM≌△ACM
∴CD=CA,DM=AM,∠DCM=∠ACM,∠CDM=∠A
又∵CA=CB,
∴CD=CB,
∴∠DCN=∠ECF﹣∠DCM=45°﹣∠DCM
∠BCN=∠ACB﹣∠ECF﹣∠ACM
=90°﹣45°﹣∠ACM=45°﹣∠ACM
∴∠DCN=∠BCN
又∵CN=CN,
∴△CDN≌△CBN.
∴DN=BN,∠CDN=∠B.
∴∠MDN=∠CDM+∠CDN=∠A+∠B=90°.
∴在Rt△MDN中,由勾股定理
∴MN2=DM2+DN2,即MN2=AM2+BN2.
(Ⅱ)解:关系式MN2=AM2+BN2仍然成立.
证明:∵将△ACM沿直线CE对折,得△GCM,连GN,
∴△GCM≌△ACM.(8分)
∴CG=CA,GM=AM,∠GCM=∠ACM,∠CGM=∠CAM,
又∵CA=CB,得CG=CB.
∵∠GCN=∠GCM+∠ECF=∠GCM+45°
∴∠BCN=∠ACB﹣∠ACN=90°﹣(∠ECF﹣∠ACM)=45°+∠ACM
得∠GCN=∠BCN.
又∵CN=CN,
∴△CGN≌△CBN.
∴GN=BN,∠CGN=∠B=45°,∠CGM=∠CAM=180°﹣∠CAB=135°,
∴∠MGN=∠CGM﹣∠CGN=135°﹣45°=90°,
∴在Rt△MGN中,由勾股定理,
∴MN2=GM2+GN2,即MN2=AM2+BN2.
1.如图,在5×5正方形网格中,一条圆弧经过A、B、C三点,那么这条圆弧所在的圆的圆心为图中的( )
A.M
B.P
C.Q
D.R
2.已知AB是半径为1的圆O的一条弦,且AB=a<1,以AB为一边在圆O内作正△ABC,点D为圆O上不同于点A的一点,且DB=AB=a,DC的延长线交圆O于点E,则AE的长为( )
A.
B.1
C.
D.a
3.如图,在⊙O中,分别将、沿两条互相平行的弦AB、CD折叠,折叠后的弧均过圆心,若⊙O的半径为4,则四边形ABCD的面积是( )
A.8
B.16
C.32
D.32
4.如图,⊙O的半径OA=15,弦DE⊥AB于点C,若OC:BC=3:2,则DE的长为
.
5.在圆柱形油罐内装进一些油后,其横截面如图.若油面宽AB=800mm,油的最大深度为200mm,则该油罐横截面的半径是
mm.
6.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=4cm,则球的半径为
cm.
7.如图,E是⊙O的直径AB上一点,AB=10,BE=2,过点E作弦CD⊥AB,P是上一动点,连接DP,过点A作AQ⊥PD,垂足为Q,则OQ的最小值为
.
8.如图,圆心在y轴的负半轴上,半径为5的⊙B与y轴的正半轴交于点A(0,1),过点P(0,﹣7)的直线l与⊙B相交于C,D两点,则弦CD长的所有可能的整数值有
个.
9.如图⊙O半径为2,弦AB∥弦CD,AB=2,CD=2,则AB和CD之间的距离
.
10.如图,在⊙O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP⊥PQ,当点P在BC上移动时,则PQ长的最大值为
.
11.如图,△ABC中,∠A=70°,⊙O截△ABC的三条边所截得弦长相等,则∠BOC=
.
12.如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C,D两点,点E为⊙G上一动点,CF⊥AE于F,则弦AB的长度为
;当点E在⊙O的运动过程中,线段FG的长度的最小值为
.
13.如图,⊙O的弦AB、CD相交于点P,且AB=CD.求证PB=PD.
14.如图AB、CD是⊙O的直径,弦CE∥AB,所对的圆心角为30°.求∠AOC的度数.
15.已知⊙O经过四边形ABCD的B、D两点,并与四条边分别交于点E、F、G、H,且=.
(1)如图①,连接BD,若BD是⊙O的直径,求证:∠A=∠C;
(2)如图②,若的度数为θ,∠A=α,∠C=β,请直接写出θ、α和β之间的数量关系.
16.如图,要把破残的圆片复制完整,已知弧上的点A、B、C.
(1)试确定所在圆的圆心O;
(2)设△ABC是等腰三角形,底边BC=10厘米,腰AB=6厘米,求圆片的半径R.(结果保留根号)
17.如图,⊙O的弦AB、CD的延长线相交于点P,且PB=PD.求证:AB=CD.
18.如图,将一个两边带有刻度的直尺放在半圆形纸片上,使其一边经过圆心O,另一边所在直线与半圆交于点D、E,量出半径OC=5cm,弦DE=8cm,求直尺的宽.
车辆转弯时,能否顺利通过直角弯道的标准是:车辆是否可以行使到和路的边界夹角是45°的位置(如图1中②的位置),例如,图2是某巷子的俯视图,巷子路面宽4m,转弯处为直角,车辆的车身为矩形ABCD,CD与DE、CE的夹角都是45°时,连接EF,交CD于点G,若GF的长度至少能达到车身宽度,则车辆就能通过.
(1)试说明长8m,宽3m的消防车不能通过该直角转弯;
(2)为了能使长8m,宽3m的消防车通过该弯道,可以将转弯处改为圆弧(分别是以O为圆心,以OM和ON为半径的弧),具体方案如图3,其中OM⊥OM′,请你求出ON的最小值.
20.如图,在半径为5的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E.
(1)当BC=6时,求线段OD的长;
(2)在△DOE中是否存在长度保持不变的边?如果存在,请指出并求其长度;如果不存在,请说明理由.
21.已知Rt△ABC中,∠ACB=90°,CA=CB,有一个圆心角为45°,半径的长等于CA的扇形CEF绕点C旋转,且直线CE,CF分别与直线AB交于点M,N.
(Ⅰ)当扇形CEF绕点C在∠ACB的内部旋转时,如图1,求证:MN2=AM2+BN2;
(思路点拨:考虑MN2=AM2+BN2符合勾股定理的形式,需转化为在直角三角形中解决.可将△ACM沿直线CE对折,得△DCM,连DN,只需证DN=BN,∠MDN=90°就可以了.请你完成证明过程.)
(Ⅱ)当扇形CEF绕点C旋转至图2的位置时,关系式MN2=AM2+BN2是否仍然成立?若成立,请证明;若不成立,请说明理由.
参考答案
1.解:作AB的垂直平分线,作BC的垂直平分线,如图,
它们都经过Q,所以点Q为这条圆弧所在圆的圆心.
故选:C.
2.解:∵△ABC是等边三角形,
∴AB=BC=AC=BD=a,∠CAB=∠ACB=60°;
∵AB=BD,
∴,
∴∠AED=∠AOB;
∵BC=AB=BD,
∴∠D=∠BCD;
∵四边形EABD内接于⊙O,
∴∠EAB+∠D=180°,即∠EAC+60°+∠D=180°;
又∵∠ECA+60°+∠BCD=180°,
∴∠ECA=∠EAC,即△EAC是等腰三角形;
在等腰△EAC和等腰△OAB中,∠AEC=∠AOB,
∵AC=AB,
∴△EAC≌△OAB;
∴AE=OA=1.
故选:B.
3.解:过O作OH⊥AB交⊙O于E,反向延长EO交CD于G,交⊙O于F,
连接OA,OB,OD,
∵AB∥CD,
∴EF⊥CD,
∵分别将、沿两条互相平行的弦AB、CD折叠,折叠后的弧均过圆心,
∴OH=OA,
∴∠HAO=30°,
∴∠AOH=60°,
同理∠DOG=60°,
∴∠AOD=60°,
∴△AOD是等边三角形,
∵OA=OB,
∴∠ABO=∠BAO=30°,
∴∠AOB=120°,
∴∠AOD+∠AOB=180°,
∴D,O,B三点共线,且BD为⊙O的直径,
∴∠DAB=90°,
同理,∠ABC=∠ADC=90°,
∴四边形ABCD是矩形,
∴AD=AO=4,AB=AD=4,
∴四边形ABCD的面积是16,
故选:B.
4.解:连接OD.
∵OA=OB=15,OC:BC=3:2,
∴BC=6,OC=9,
∵AB⊥DE,
∴CD=CE===12,
∴DE=2CD=24,
故答案为:24.
5.解:过O作OD⊥AB于C,交圆O于D,连接OA,如图所示:
则AC=BC=AB=400(mm),CD=200mm,
设该油罐横截面的半径为xmm,则OC=(x﹣200)mm,
在Rt△AOC中,由勾股定理得:4002+(x﹣200)2=x2,
解得:x=500,
即该油罐横截面的半径为500mm,
故答案为:500.
6.解:EF的中点M,作MN⊥AD于点M,取MN上的球心O,连接OF,
∵四边形ABCD是矩形,
∴∠C=∠D=90°,
∴四边形CDMN是矩形,
∴MN=CD=4,
设OF=x,则ON=OF,
∴OM=MN﹣ON=4﹣x,MF=2,
在直角三角形OMF中,OM2+MF2=OF2
即:(4﹣x)2+22=x2
解得:x=2.5
故答案为:2.5
7.解:∵AQ⊥PD,垂足为Q,
∴∠AQD=90°,
∴点Q在以AD为直径的圆上,
连接AD,以AD为直径作⊙M,如图,
连接MO并延长交⊙M于Q′,
当Q点运动到Q′时,OQ的值最小,
连接OD,
在Rt△ODE中,∵OD=5,OE=5﹣2=3,
∴DE==4,
在Rt△ADE中,AD==4,
∴MA=MQ′=2,
在Rt△AOM中,OM==,
∴OQ′=MQ′﹣OM=2﹣=,
∴OQ的最小值为.
故答案为.
8.解:∵点A的坐标为(0,1),圆的半径为5,
∴点B的坐标为(0,﹣4),
又∵点P的坐标为(0,﹣7),
∴BP=3,
①当CD垂直圆的直径AE时,CD的值最小,
连接BC,
在Rt△BCP中,CP==4;
故CD=2CP=8,
②当CD经过圆心时,CD的值最大,此时CD=直径AE=10;
所以,8≤CD≤10,
所以符合的弦有4条,整数值是8(一条弦),9(两条弦),10(一条弦),
综上可得:弦CD长的所有可能的整数值有:8,9,10,共3个,
故答案为:3.
9.解:①当弦AB和CD在圆心同侧时,如图1所示,
∵AB=2,CD=2,
∴AF=1,CE=,
∵OA=OC=2,
∴EO===,OF==,
∴EF=OF﹣OE=﹣;
②当弦AB和CD在圆心异侧时,如图2所示,
∵AB=2,CD=2,
∴AE=1,CF=,
∵OA=OC=2,
同法可得EO=,OF=,
∴EF=OF+OE=+;
综上所述:AB和CD之间的距离为﹣或+.
故答案为:﹣或+.
10.解:如图2中连接OQ,∵PQ=,OQ为定值,
∴当OP⊥BC时,OP的值最小,此时PQ长的最大.
此时OP=OB=,
在Rt△OPQ中,PQ==.
故答案为.
11.解:过O作OM⊥AB于M,ON⊥BC于N,OQ⊥AC于Q,连接OK、OD、OF、OB、OC,设AB,AC,BC与⊙O的另一个交点分别为E,H,G.
由垂径定理得:DM=DE,KQ=KH,FN=FG,
∵DE=FG=HK,
∴DM=KQ=FN,
∵OD=OK=OF,
∴由勾股定理得:OM=ON=OQ,
即O到三角形ABC三边的距离相等,
∴O是△ABC的内心,
∴∠OBC+∠OCB=(180°﹣70°)=55°,
∴∠BOC=125°,
故答案为125°.
12.解:作GM⊥AC于M,连接AG.
∵GO⊥AB,
∴OA=OB,
在Rt△AGO中,∵AG=2,OG=1,
∴AG=2OG,OA==,
∴∠GAO=30°,AB=2AO=2,
∴∠AGO=60°,
∵GC=GA,
∴∠GCA=∠GAC,
∵∠AGO=∠GCA+∠GAC,
∴∠GCA=∠GAC=30°,
∴AC=2OA=2,MG=CG=1,
∵∠AFC=90°,
∴点F在以AC为直径的⊙M上,
当点F在MG的延长线上时,FG的长最小,最小值=FM﹣GM=﹣1.
故答案为2,﹣1.
13.证明:连接BD.
∵AB=CD,
∴=
∴﹣=﹣,即=,
∴∠B=∠D,
∴PB=PD.
14.解:连接OE,如图,
∵为30°,
∴∠COE=30°,
∵OC=OE,
∴∠OCE=∠OEC,
∴∠OCE=(180°﹣30°)÷2=75°,
∵弦CE∥AB,
∴∠AOC=∠OCE=75°.
15.解:(1)连接DF、DG.
∵BD是⊙O的直径,
∴∠DFB=∠DGB=90°,
∵=,
∴∠EDF=∠HDG,
∵∠DFB=∠EDF+∠A,
∠DGB=∠HDG+∠C,
∴∠A=∠C.
(2)结论:α+β+θ=180°.
理由:如图②中,连接DF,BH.
∵=,
∴∠ADF=∠HBG=θ,
∵∠AFD+∠DFB=180°,∠DFB+∠DHB=180°,
∴∠AFD=∠DHB,
∵∠A+∠ADF+∠AFD=180°,∠AFD=∠DHB=∠C+∠HBG,
∴∠A+θ+∠C+θ=180°,
∴α+β+θ=180°.
16.解:(1)作DO⊥AB.DO必过圆心,作EO⊥AC,EO必过圆心,DO、EO交点必为圆心;
(2)
设半径为r.连接OA,因为BA=AC,故AO⊥BC.
所以:CD=×10=5,AD==.
根据勾股定理,(R﹣)2+52=R2,解得R=.
17.证明:如图,连接BD
∵PB=PD
∴∠PBD=∠PDB,
∴优弧=优弧,
∴﹣=﹣,即=,
∴AB=CD.
18.解:过点O作OM⊥DE于点M,连接OD.
∴DM=DE.
∵DE=8(cm)
∴DM=4(cm)
在Rt△ODM中,∵OD=OC=5(cm),
∴OM===3(cm)
∴直尺的宽度为3cm.
19.解:(1)消防车不能通过该直角转弯.
理由如下:如图,作FH⊥EC,垂足为H,
∵FH=EH=4,
∴EF=4,且∠GEC=45°,
∵GC=4,
∴GE=GC=4,
∴GF=4﹣4<3,
即GF的长度未达到车身宽度,
∴消防车不能通过该直角转弯;
(2)若C、D分别与M′、M重合,则△OGM为等腰直角三角形,
∴OG=4,OM=4,
∴OF=ON=OM﹣MN=4﹣4,
∴FG=OG﹣OF=×8﹣(4﹣4)=8﹣4<3,
∴C、D在上,
设ON=x,连接OC,在Rt△OCG中,
OG=x+3,OC=x+4,CG=4,
由勾股定理得,OG2+CG2=OC2,
即(x+3)2+42=(x+4)2,
解得x=4.5.
答:ON至少为4.5米.
20.解:(1)如图(1),
∵OD⊥BC,
∴BD=BC=×6=3,
∵∠BDO=90°,OB=5,BD=3,
∴OD==4,
即线段OD的长为4.
(2)存在,DE保持不变.
理由:连接AB,如图(2),
∵∠AOB=90°,OA=OB=5,
∴AB==5,
∵OD⊥BC,OE⊥AC,
∴D和E分别是线段BC和AC的中点,
∴DE=AB=,
∴DE保持不变.
21.(Ⅰ)证明:∵将△ACM沿直线CE对折,得△DCM,连DN,
∴△DCM≌△ACM
∴CD=CA,DM=AM,∠DCM=∠ACM,∠CDM=∠A
又∵CA=CB,
∴CD=CB,
∴∠DCN=∠ECF﹣∠DCM=45°﹣∠DCM
∠BCN=∠ACB﹣∠ECF﹣∠ACM
=90°﹣45°﹣∠ACM=45°﹣∠ACM
∴∠DCN=∠BCN
又∵CN=CN,
∴△CDN≌△CBN.
∴DN=BN,∠CDN=∠B.
∴∠MDN=∠CDM+∠CDN=∠A+∠B=90°.
∴在Rt△MDN中,由勾股定理
∴MN2=DM2+DN2,即MN2=AM2+BN2.
(Ⅱ)解:关系式MN2=AM2+BN2仍然成立.
证明:∵将△ACM沿直线CE对折,得△GCM,连GN,
∴△GCM≌△ACM.(8分)
∴CG=CA,GM=AM,∠GCM=∠ACM,∠CGM=∠CAM,
又∵CA=CB,得CG=CB.
∵∠GCN=∠GCM+∠ECF=∠GCM+45°
∴∠BCN=∠ACB﹣∠ACN=90°﹣(∠ECF﹣∠ACM)=45°+∠ACM
得∠GCN=∠BCN.
又∵CN=CN,
∴△CGN≌△CBN.
∴GN=BN,∠CGN=∠B=45°,∠CGM=∠CAM=180°﹣∠CAB=135°,
∴∠MGN=∠CGM﹣∠CGN=135°﹣45°=90°,
∴在Rt△MGN中,由勾股定理,
∴MN2=GM2+GN2,即MN2=AM2+BN2.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
