2021-2022学年数学鲁教版七年级上册3.1探索勾股定理同步课时作业(word解析版)
文档属性
| 名称 | 2021-2022学年数学鲁教版七年级上册3.1探索勾股定理同步课时作业(word解析版) |
|
|
| 格式 | docx | ||
| 文件大小 | 402.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-29 23:18:35 | ||
图片预览


文档简介
3.1探索勾股定理—2021-2022学年数学鲁教版七年级上册同步课时作业
1.在中,,
cm,
cm,则AB等于(
)
A.2
cm
B.10
cm
C.8
cm
D.100
cm
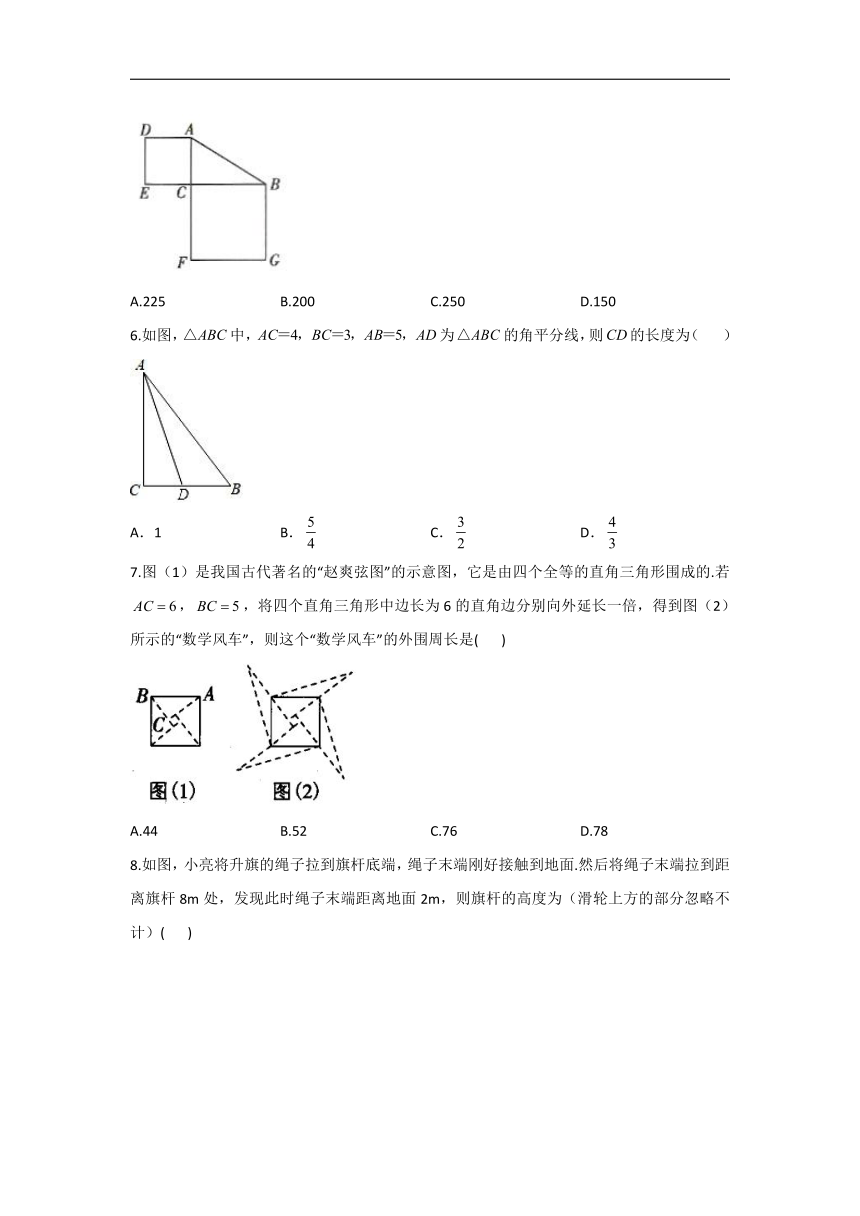
2.如图,长为8cm的橡皮筋放置在x轴上,固定两端A和B,然后把中点C向上拉高3cm至点D,则橡皮筋被拉长了(
)
A.2
cm
B.3
cm
C.4
cm
D.5
cm
3.已知中,,若,则的面积为(
)
A.9
B.18
C.24
D.36
4.下列选项中,不能用来证明勾股定理的是(
)
A.
B.
C.
D.
5.如图,在中,,若,则正方形和正方形的面积和为(
)
A.225
B.200
C.250
D.150
6.如图,中,为的角平分线,则的长度为(
)
A.1
B.
C.
D.
7.图(1)是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若,,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图(2)所示的“数学风车”,则这个“数学风车”的外围周长是(
)
A.44
B.52
C.76
D.78
8.如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面.然后将绳子末端拉到距离旗杆8m处,发现此时绳子末端距离地面2m,则旗杆的高度为(滑轮上方的部分忽略不计)(
)
A.12m
B.13m
C.17m
D.16m
9.如图,在中,CE平分,CF平分,且交边AC于点M.若,则等于(
)
A.75
B.100
C.120
D.125
10.若三个连续的正整数是勾股数,则这三个数为_________;若三个连续的偶数是勾股数,则这三个数为__________.
11.在直线l上依次摆放着七个正方形(如图).已知斜放置的三个正方形的面积分别是1,2,3,正放置的四个正方形的面积依次是,则_________.
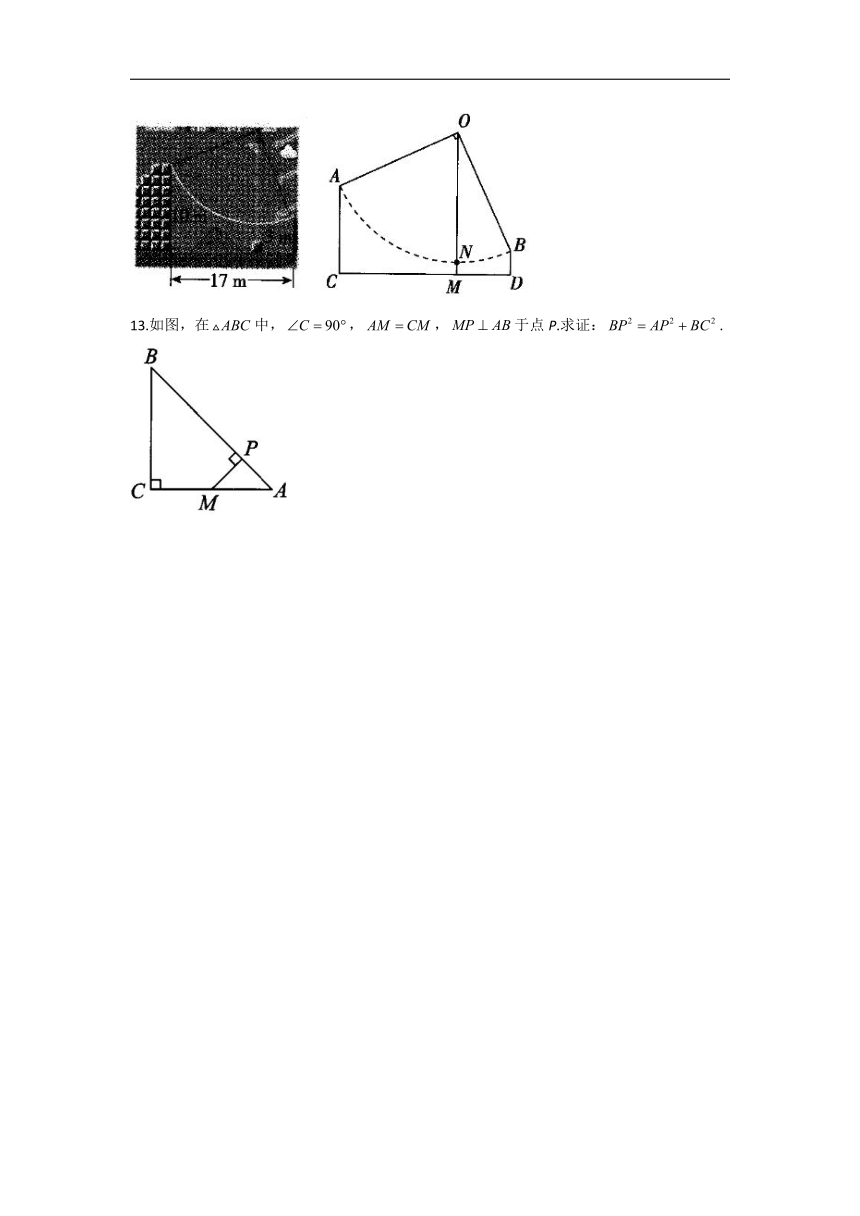
12.如图,玛丽(视为小黑点)站在一个高为10m的高台A上,利用旗杆OM顶部的绳索,划过90°到达与高台A水平距离为17m、高为3m的矮台B,玛丽在荡绳索的过程中的最低点离地面的高度__________m.
13.如图,在中,,,于点P.求证:.
答案以及解析
1.答案:B
解析:因为在中,,
cm,
cm.由勾股定理,得,所以cm(负值已舍去).故选B.
2.答案:A
解析:中,cm,cm,根据勾股定理,得,
cm,(cm),橡皮筋被拉长了2cm.故选A.
3.答案:A
解析:,又,
,解得,
的面积为9.故选A.
4.答案:C
解析:A.,,能证明勾股定理;B.,能证明勾股定理;C.根据图形不能证明勾股定理;D.,能证明勾股定理.故选C.
5.答案:A
解析:正方形的面积,正方形的面积.在中,,,则.故选A.
6.答案:D
解析:∵,
∴,
∴,
过作于,
∵平分,
∴,
∵,
∴,
∴.
故选:D.
7.答案:D
解析:如图,在中,,,,由勾股定理,得,.,这个“数学风车”的外围周长是76.故选C.
8.答案:C
解析:如答图,设旗杆的高度为xm(),则m,
m.在中,
m,由勾股定理,得,即,解得,即旗杆的高度为17m.故选C.
9.答案:B
解析:因为CE平分,CF平分,所以,,所以,所以为直角三角形.又因为,CE平分,CF平分,所以,,所以,所以.在中,由勾股定理,得.故选B.
10.答案:3,4,5;6,8,10
11.答案:2
解析:如图,在和中,,
,
,,同理可证,..
12.答案:2
解析:如图,作于点E,作于点F,.,.在和中,,,,,
m.(m),m,则m,m,m,m.由勾股定理得m,m,(m),即玛丽在荡绳索的过程中的最低点离地面的高度MN为2m.
13.答案:证明:连接BM.
因为是直角三角形,且,
所以,
在中,①.
因为,,
所以②.
因为与都是直角三角形,
所以,
所以③.
把①③代入②,得,即.
1.在中,,
cm,
cm,则AB等于(
)
A.2
cm
B.10
cm
C.8
cm
D.100
cm
2.如图,长为8cm的橡皮筋放置在x轴上,固定两端A和B,然后把中点C向上拉高3cm至点D,则橡皮筋被拉长了(
)
A.2
cm
B.3
cm
C.4
cm
D.5
cm
3.已知中,,若,则的面积为(
)
A.9
B.18
C.24
D.36
4.下列选项中,不能用来证明勾股定理的是(
)
A.
B.
C.
D.
5.如图,在中,,若,则正方形和正方形的面积和为(
)
A.225
B.200
C.250
D.150
6.如图,中,为的角平分线,则的长度为(
)
A.1
B.
C.
D.
7.图(1)是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若,,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图(2)所示的“数学风车”,则这个“数学风车”的外围周长是(
)
A.44
B.52
C.76
D.78
8.如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面.然后将绳子末端拉到距离旗杆8m处,发现此时绳子末端距离地面2m,则旗杆的高度为(滑轮上方的部分忽略不计)(
)
A.12m
B.13m
C.17m
D.16m
9.如图,在中,CE平分,CF平分,且交边AC于点M.若,则等于(
)
A.75
B.100
C.120
D.125
10.若三个连续的正整数是勾股数,则这三个数为_________;若三个连续的偶数是勾股数,则这三个数为__________.
11.在直线l上依次摆放着七个正方形(如图).已知斜放置的三个正方形的面积分别是1,2,3,正放置的四个正方形的面积依次是,则_________.
12.如图,玛丽(视为小黑点)站在一个高为10m的高台A上,利用旗杆OM顶部的绳索,划过90°到达与高台A水平距离为17m、高为3m的矮台B,玛丽在荡绳索的过程中的最低点离地面的高度__________m.
13.如图,在中,,,于点P.求证:.
答案以及解析
1.答案:B
解析:因为在中,,
cm,
cm.由勾股定理,得,所以cm(负值已舍去).故选B.
2.答案:A
解析:中,cm,cm,根据勾股定理,得,
cm,(cm),橡皮筋被拉长了2cm.故选A.
3.答案:A
解析:,又,
,解得,
的面积为9.故选A.
4.答案:C
解析:A.,,能证明勾股定理;B.,能证明勾股定理;C.根据图形不能证明勾股定理;D.,能证明勾股定理.故选C.
5.答案:A
解析:正方形的面积,正方形的面积.在中,,,则.故选A.
6.答案:D
解析:∵,
∴,
∴,
过作于,
∵平分,
∴,
∵,
∴,
∴.
故选:D.
7.答案:D
解析:如图,在中,,,,由勾股定理,得,.,这个“数学风车”的外围周长是76.故选C.
8.答案:C
解析:如答图,设旗杆的高度为xm(),则m,
m.在中,
m,由勾股定理,得,即,解得,即旗杆的高度为17m.故选C.
9.答案:B
解析:因为CE平分,CF平分,所以,,所以,所以为直角三角形.又因为,CE平分,CF平分,所以,,所以,所以.在中,由勾股定理,得.故选B.
10.答案:3,4,5;6,8,10
11.答案:2
解析:如图,在和中,,
,
,,同理可证,..
12.答案:2
解析:如图,作于点E,作于点F,.,.在和中,,,,,
m.(m),m,则m,m,m,m.由勾股定理得m,m,(m),即玛丽在荡绳索的过程中的最低点离地面的高度MN为2m.
13.答案:证明:连接BM.
因为是直角三角形,且,
所以,
在中,①.
因为,,
所以②.
因为与都是直角三角形,
所以,
所以③.
把①③代入②,得,即.
