2021-2022学年数学冀教版九年级上册25.7相似多边形和图形的位似_同步课时作业(word解析版)
文档属性
| 名称 | 2021-2022学年数学冀教版九年级上册25.7相似多边形和图形的位似_同步课时作业(word解析版) |
|
|
| 格式 | docx | ||
| 文件大小 | 388.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-29 00:00:00 | ||
图片预览


文档简介
25.7相似多边形和图形的位似—2021-2022学年数学冀教版九年级上册同步课时作业
1.如果两个相似多边形的一组对应边长分别为3
cm和2
cm,那么它们的相似比是(
)
A.
B.
C.
D.
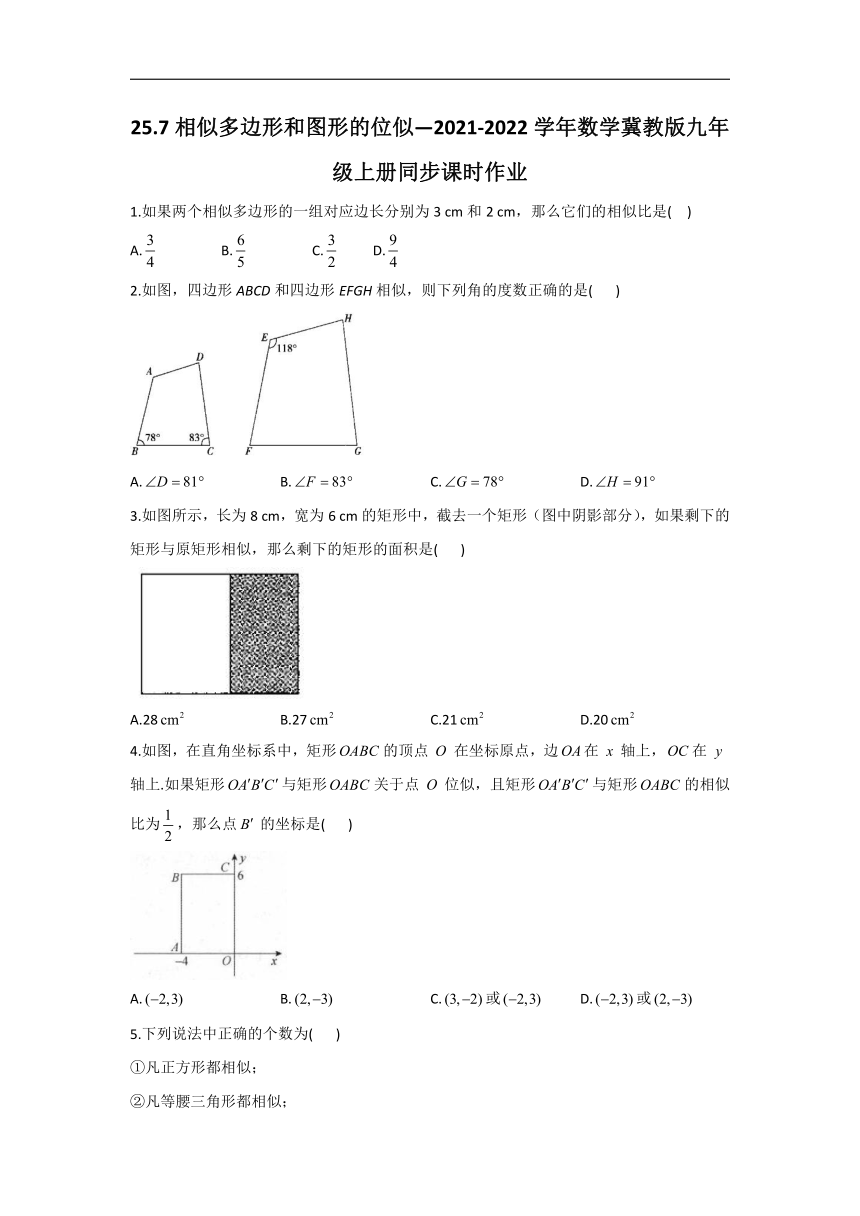
2.如图,四边形ABCD和四边形EFGH相似,则下列角的度数正确的是(
)
A.
B.
C.
D.
3.如图所示,长为8
cm,宽为6
cm的矩形中,截去一个矩形(图中阴影部分),如果剩下的矩形与原矩形相似,那么剩下的矩形的面积是(
)
A.28
B.27
C.21
D.20
4.如图,在直角坐标系中,矩形的顶点在坐标原点,边在轴上,在轴上.如果矩形与矩形关于点位似,且矩形与矩形的相似比为,那么点的坐标是(
)
A.
B.
C.或
D.或
5.下列说法中正确的个数为(
)
①凡正方形都相似;
②凡等腰三角形都相似;
③凡等腰直角三角形都相似;
④两个相似多边形的面积比为4:9,则周长的比为16:81.
A.1
B.2
C.3
D.4
6.如图,线段AB两个端点的坐标分别为,,以原点O为位似中心,将线段AB缩小为原来的,得到线段CD,则线段AB的中点E的对应点的坐标为(
)
A.
B.
C.或
D.或
7.小刚家的电视机有画中画功能,他可以通过屏幕(矩形)右下角的小画面(矩形)查看别的电视节目(如图).已知小画面与电视机屏幕相似,且各边长是对应边长的,则下列说法错误的是(
)
A.小画面与屏幕的周长的比为
B.小画面与屏幕的面积的比为
C.小画面的矩形与屏幕的矩形是位似图形
D.小画面与屏幕的面积的比为
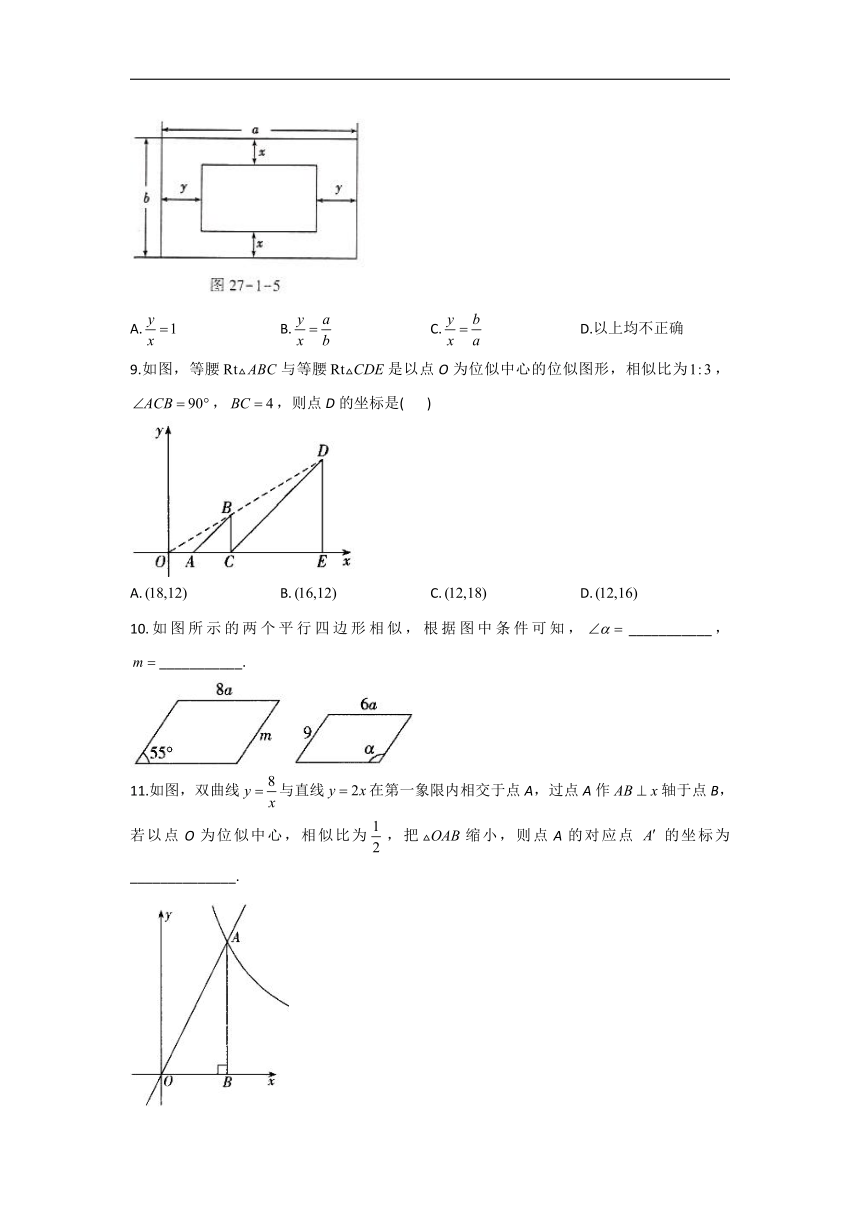
8.如图27-1-5,内外两个四边形相似,且对应边互相平行,则下列结论正确的是(
)
A.
B.
C.
D.以上均不正确
9.如图,等腰与等腰是以点O为位似中心的位似图形,相似比为,,,则点D的坐标是(
)
A.
B.
C.
D.
10.如图所示的两个平行四边形相似,根据图中条件可知,___________,___________.
11.如图,双曲线与直线在第一象限内相交于点A,过点A作轴于点B,若以点O为位似中心,相似比为,把缩小,则点A的对应点的坐标为______________.
12.如图,点E,F分别是矩形纸片ABCD的边AD,BC的三等分点(分别靠近点D、C),沿EF将矩形纸片EFCD剪下来,然后将矩形纸片EFCD对折折痕为GH,若矩形矩形ABCD,则的值为____________.
13.如图,在平面直角坐标系中,的顶点坐标分别为,,.
(1)的面积是__________;
(2)请以原点O为位似中心,画出,使它与的相似比为,变换后点A、B的对应点分别为点、,点在第一象限;
(3)在(2)的条件下,若为线段BC上的任意一点,则变换后点P的对应点的坐标为.
答案以及解析
1.答案:C
解析:∵两个相似多边形的一组对应边分别为3cm和2
cm,
∴它们的相似比为.故选C.
2.答案:A
解析:四边形ABCD和四边形EFGH相似,,,,.故选A.
3.答案:B
解析:如图,因为矩形ABCD与矩形DEFC相似,所以,设,则,解得,经检验,是原方程的解,所以剩下的矩形的面积是.故选B.
4.答案:D
解析:矩形和关于点位似,相似比为,且点的坐标为.
点的坐标为或.
5.答案:B
解析:①所有正方形的边成比例,角相等,都相似,故①正确;②等腰三角形形状不一定相同,所以不一定相似,故②错误;③所有等腰直角三角形的边成比例,角分别相等,都相似,故③正确;④两个相似多边形的面积比为4:9,则周长的比为2:3,故④错误.所以说法正确的有①③,共2个.故选B.
6.答案:C
解析:,,AB的中点E的坐标为.以原点O为位似中心,将线段AB缩小为原来的,点E的对应点的坐标为或,即或.故选C.
7.答案:B
解析:小画面与电视机屏幕相似,且各边长是对应边长的,周长的比为,面积的比为,故A、D说法正确,B说法错误;小画面与电视机屏幕相似,对应顶点的连线相交于右下角的顶点,是位似图形,故C说法正确.故选B.
8.答案:B
解析:题图内外两个四边形相似,对应边的比相等,即故选B.
9.答案:A
解析:由题意,得,相似比为,则.,.是等腰直角三角形,,,解得,故,.故选A.
10.答案:125°;12
解析:如图,四边形ABCD是平行四边形,,,.两个平行四边形相似,,,解得.
11.答案:或
解析:解方程组得或.
点A在第一象限内,,
点的坐标为或,即点的坐标为或.
12.答案:
解析:设,,由题意得,,矩形与矩形ABCD,,即,,,.
13.答案:(1)12.
(2)如图,即为所求作三角形.
(3).
1.如果两个相似多边形的一组对应边长分别为3
cm和2
cm,那么它们的相似比是(
)
A.
B.
C.
D.
2.如图,四边形ABCD和四边形EFGH相似,则下列角的度数正确的是(
)
A.
B.
C.
D.
3.如图所示,长为8
cm,宽为6
cm的矩形中,截去一个矩形(图中阴影部分),如果剩下的矩形与原矩形相似,那么剩下的矩形的面积是(
)
A.28
B.27
C.21
D.20
4.如图,在直角坐标系中,矩形的顶点在坐标原点,边在轴上,在轴上.如果矩形与矩形关于点位似,且矩形与矩形的相似比为,那么点的坐标是(
)
A.
B.
C.或
D.或
5.下列说法中正确的个数为(
)
①凡正方形都相似;
②凡等腰三角形都相似;
③凡等腰直角三角形都相似;
④两个相似多边形的面积比为4:9,则周长的比为16:81.
A.1
B.2
C.3
D.4
6.如图,线段AB两个端点的坐标分别为,,以原点O为位似中心,将线段AB缩小为原来的,得到线段CD,则线段AB的中点E的对应点的坐标为(
)
A.
B.
C.或
D.或
7.小刚家的电视机有画中画功能,他可以通过屏幕(矩形)右下角的小画面(矩形)查看别的电视节目(如图).已知小画面与电视机屏幕相似,且各边长是对应边长的,则下列说法错误的是(
)
A.小画面与屏幕的周长的比为
B.小画面与屏幕的面积的比为
C.小画面的矩形与屏幕的矩形是位似图形
D.小画面与屏幕的面积的比为
8.如图27-1-5,内外两个四边形相似,且对应边互相平行,则下列结论正确的是(
)
A.
B.
C.
D.以上均不正确
9.如图,等腰与等腰是以点O为位似中心的位似图形,相似比为,,,则点D的坐标是(
)
A.
B.
C.
D.
10.如图所示的两个平行四边形相似,根据图中条件可知,___________,___________.
11.如图,双曲线与直线在第一象限内相交于点A,过点A作轴于点B,若以点O为位似中心,相似比为,把缩小,则点A的对应点的坐标为______________.
12.如图,点E,F分别是矩形纸片ABCD的边AD,BC的三等分点(分别靠近点D、C),沿EF将矩形纸片EFCD剪下来,然后将矩形纸片EFCD对折折痕为GH,若矩形矩形ABCD,则的值为____________.
13.如图,在平面直角坐标系中,的顶点坐标分别为,,.
(1)的面积是__________;
(2)请以原点O为位似中心,画出,使它与的相似比为,变换后点A、B的对应点分别为点、,点在第一象限;
(3)在(2)的条件下,若为线段BC上的任意一点,则变换后点P的对应点的坐标为.
答案以及解析
1.答案:C
解析:∵两个相似多边形的一组对应边分别为3cm和2
cm,
∴它们的相似比为.故选C.
2.答案:A
解析:四边形ABCD和四边形EFGH相似,,,,.故选A.
3.答案:B
解析:如图,因为矩形ABCD与矩形DEFC相似,所以,设,则,解得,经检验,是原方程的解,所以剩下的矩形的面积是.故选B.
4.答案:D
解析:矩形和关于点位似,相似比为,且点的坐标为.
点的坐标为或.
5.答案:B
解析:①所有正方形的边成比例,角相等,都相似,故①正确;②等腰三角形形状不一定相同,所以不一定相似,故②错误;③所有等腰直角三角形的边成比例,角分别相等,都相似,故③正确;④两个相似多边形的面积比为4:9,则周长的比为2:3,故④错误.所以说法正确的有①③,共2个.故选B.
6.答案:C
解析:,,AB的中点E的坐标为.以原点O为位似中心,将线段AB缩小为原来的,点E的对应点的坐标为或,即或.故选C.
7.答案:B
解析:小画面与电视机屏幕相似,且各边长是对应边长的,周长的比为,面积的比为,故A、D说法正确,B说法错误;小画面与电视机屏幕相似,对应顶点的连线相交于右下角的顶点,是位似图形,故C说法正确.故选B.
8.答案:B
解析:题图内外两个四边形相似,对应边的比相等,即故选B.
9.答案:A
解析:由题意,得,相似比为,则.,.是等腰直角三角形,,,解得,故,.故选A.
10.答案:125°;12
解析:如图,四边形ABCD是平行四边形,,,.两个平行四边形相似,,,解得.
11.答案:或
解析:解方程组得或.
点A在第一象限内,,
点的坐标为或,即点的坐标为或.
12.答案:
解析:设,,由题意得,,矩形与矩形ABCD,,即,,,.
13.答案:(1)12.
(2)如图,即为所求作三角形.
(3).
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
