3.1.1函数的概念(教案)-高中数学人教A版(2019)必修第一册
文档属性
| 名称 | 3.1.1函数的概念(教案)-高中数学人教A版(2019)必修第一册 |

|
|
| 格式 | doc | ||
| 文件大小 | 299.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-29 14:03:14 | ||
图片预览


文档简介
第三章
函数的概念与性质
3.1.1
函数的概念
教学设计
一、教学目标
1.通过具体教学实例,在体会两个变量之间依赖关系的基础上,引导学生运用集合思想与对应的语言刻画函数概念,促进学生数学抽象核心素养的发展,达到水平二的要求.
2.能够指出现实情境问题中函数的定义域和值域,达到数学计算核心素养水平一的要求.
3.给出一个函数解析式,能够举出它所对应的问题情境,达到数学建模核心素养水平一的要求.
二、教学重难点
1.教学重点
函数的概念.
简单现实情境问题的定义域和值域.
2.教学难点
给定函数解析式,如何给出所对应的现实情境.
三、教学过程
(一)探究一:函数的概念
定义:一般地,设A
,
B是非空的实数集,如果对于集合A中的任意一个数x,按照某种确定的对应关系f,在集合B中都有唯一确定的数y和它对应,那么就称f:为从集合A到集合B的一个函数,记作y=f(x),x∈A.
其中,x叫做自变量,x的取值范围A叫做函数的定义域;与x的值相对应的y值叫做函数值,函数值的集合叫做函数的值域.
函数的三个要素:定义域,对应关系,值域.
常见函数的三要素:
一次函数:的定义域是R,值域也是R.对应关系f把R中的任意一个数x,对应到R中唯一确定的数.
二次函数:的定义域是R,值域是B.当a>0时,;当a<0时,.对应关系f把R中的任意一个数x,对应到B中唯一确定的数.
反比例函数:的定义域为,对应关系为“倒数的k倍”,值域为.反比例函数用函数定义叙述为:对于非空数集中的任意一个x值,按照对应关系f:“倒数倍”,在集合中都有唯一确定的数和它对应,那么此时f:就是集合A到集合B的一个函数,记作
探究二:函数的应用
例1
函数的解析式是舍弃问题的实际背景而抽象出来的,它所反映的两个量之间的对应关系,可以广泛地用于刻画一类事物中的变量关系和规律.
例如,正比例函数可以用来刻画匀速运动中路程与时间的关系、一定密度的物体的质量与体积的关系、圆的周长与半径的关系等.
试构建一个问题情境,使其中的变量关系可以用解析式来描述.
解:把看成二次函数,那么它的定义域是R,值域是.对应关系f把R中的任意一个数x,对应到B中唯一确定的数x(10-x).
如果对x的取值范围作出限制,例如,那么可以构建如下情境:
长方形的周长为20,设一边长为x,面积为y,那么y=x(10-x).
其中,x的取值范围是,y的取值范围是.对应关系f把每一个长方形的边长x,对应到唯一确定的面积x(10-x).
探究:构建其他可用解析式y=x(10-x)描述其中变量关系的问题情境.
答案:设两个实数的和为10,其中一个数为x,这两个数的积为y,则y=x(10-x),其
中x的取值范围为A=R,y的取值范围为.对应关系f把A中任一x值对应B中唯一确定的x(10-x).
探究三:区间
定义:研究函数时常会用到区间的概念.设a,b是两个实数,而且a(1)
满足不等式的实数x的集合叫做闭区间,表示为[a,b];
(2)
满足不等式a(3)
满足不等式或的实数x的集合叫做半开半闭区间,外别表示为[a,b),(a,b].这里的实数a与b都叫做相应区间的端点.
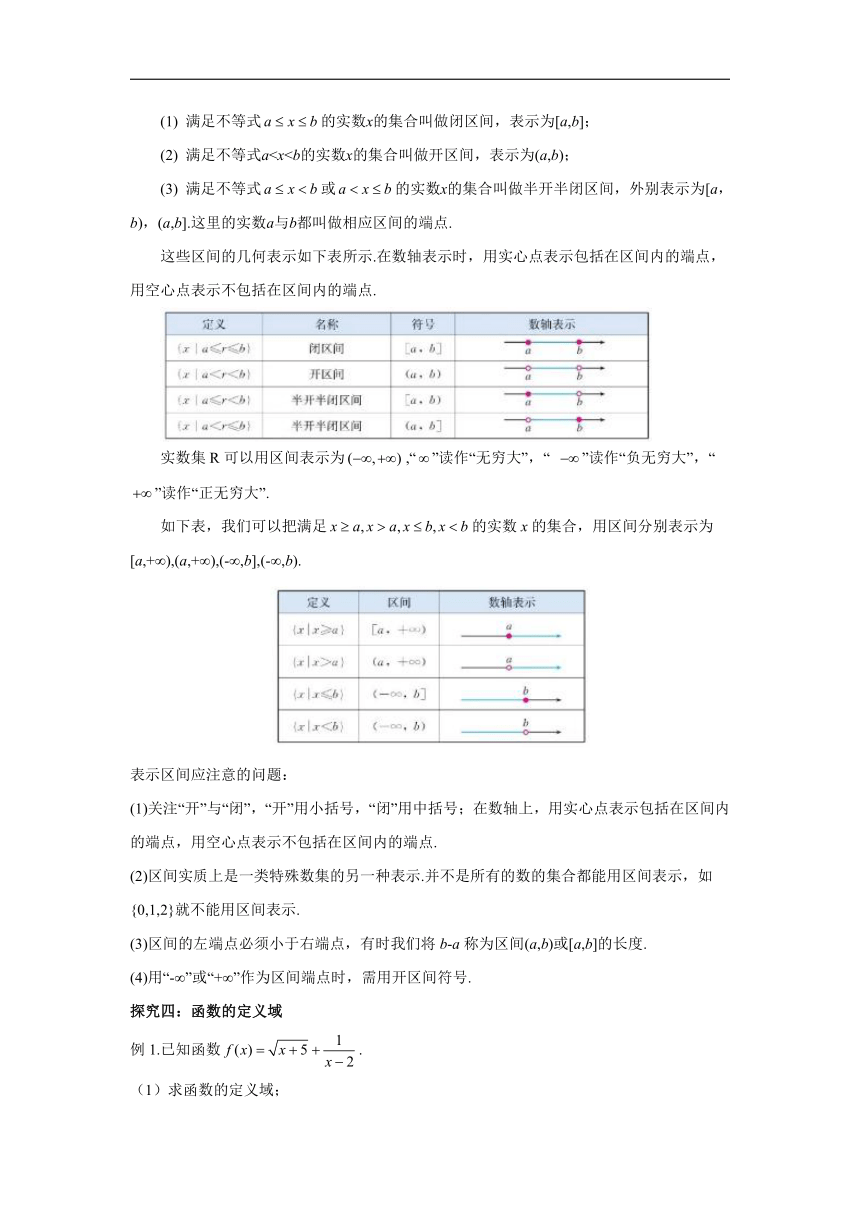
这些区间的几何表示如下表所示.在数轴表示时,用实心点表示包括在区间内的端点,用空心点表示不包括在区间内的端点.
实数集R可以用区间表示为,“”读作“无穷大”,“
”读作“负无穷大”,“
”读作“正无穷大”.
如下表,我们可以把满足的实数x的集合,用区间分别表示为
[a,+∞),(a,+∞),(-∞,b],(-∞,b).
表示区间应注意的问题:
(1)关注“开”与“闭”,“开”用小括号,“闭”用中括号;在数轴上,用实心点表示包括在区间内的端点,用空心点表示不包括在区间内的端点.
(2)区间实质上是一类特殊数集的另一种表示.并不是所有的数的集合都能用区间表示,如{0,1,2}就不能用区间表示.
(3)区间的左端点必须小于右端点,有时我们将b-a称为区间(a,b)或[a,b]的长度.
(4)用“-∞”或“+∞”作为区间端点时,需用开区间符号.
探究四:函数的定义域
例1.已知函数.
(1)求函数的定义域;
(2)求,的值.
答案:(1)使根式有意义的实数x的集合是,使分式有意义的实数x的集合是,所以函数的定义域是.
(2).
.
总结:
(1)当一个函数由两个或两个以上代数式的和、差、积、商的形式构成时,定义域是使各式子都有意义的公共部分的集合.
求函数定义域的步骤:
①列不等式(组):根据解析式有意义的条件,列出关于自变量的不等式(组)
②解不等式(组):解出所列不等式或不等式组中每个不等式的解集后在求交集
③得定义域:把不等式(组)的解集表示成集合或区间的形式
(2)已知函数解析式求函数值,可将自变量的值代入解析式求出相应的函数值.当自变量的值为包含字母的代数式时,将代数式作为一个整体代入求解.
探究五:相同函数
函数相同的条件:对应关系相同;定义域相同.
例1.判断下列各组中的两个函数是不是相同的函数.
(1),;
(2),.
答案:(1)的定义域为,而的定义域为两个函数的定义域不同,所以不是相同的函数.
(2)的定义域为,而的定义域为,两个函数的定义域不同,所以两个函数不是相同的函数.
(二)课堂练习
1.下列各图中,可表示函数的图象的是(
)
A.
B.
C.
D.
答案:D
解析:由函数的定义可知,对定义域内的任意一个变量x,都存在唯一确定的函数值y与之对应.A中,当时,有两个y与x对应;B中,当时,有两个y与x对应;C中,当时,有两个y与x对应;D中,对任意x都只有唯一确定的y与之对应.故选D.
2.不等式的解集用区间表示为(
)
A.
B.
C.
D.
答案:D
解析:由得,用区间表示为.故选D.
3.若周长为定值a的矩形,它的面积S是这个矩形的一边长x的函数,则这个函数的定义域是(
)
A.
B.
C.
D.
答案:D
解析:依题意知,矩形的一边长为x,则该边的邻边长为,由得,故这个函数的定义域是.故选D.
(三)小结作业
小结:
1.本节课我们主要学习了哪些内容?
2.函数的定义
3.函数三要素
4.区间
5.相同函数
作业:
四、板书设计
3.1.1函数的概念
1.函数的定义
2.函数三要素:定义域,对应关系,值域.
3.区间
4.相同函数:定义域,对应关系相同
函数的概念与性质
3.1.1
函数的概念
教学设计
一、教学目标
1.通过具体教学实例,在体会两个变量之间依赖关系的基础上,引导学生运用集合思想与对应的语言刻画函数概念,促进学生数学抽象核心素养的发展,达到水平二的要求.
2.能够指出现实情境问题中函数的定义域和值域,达到数学计算核心素养水平一的要求.
3.给出一个函数解析式,能够举出它所对应的问题情境,达到数学建模核心素养水平一的要求.
二、教学重难点
1.教学重点
函数的概念.
简单现实情境问题的定义域和值域.
2.教学难点
给定函数解析式,如何给出所对应的现实情境.
三、教学过程
(一)探究一:函数的概念
定义:一般地,设A
,
B是非空的实数集,如果对于集合A中的任意一个数x,按照某种确定的对应关系f,在集合B中都有唯一确定的数y和它对应,那么就称f:为从集合A到集合B的一个函数,记作y=f(x),x∈A.
其中,x叫做自变量,x的取值范围A叫做函数的定义域;与x的值相对应的y值叫做函数值,函数值的集合叫做函数的值域.
函数的三个要素:定义域,对应关系,值域.
常见函数的三要素:
一次函数:的定义域是R,值域也是R.对应关系f把R中的任意一个数x,对应到R中唯一确定的数.
二次函数:的定义域是R,值域是B.当a>0时,;当a<0时,.对应关系f把R中的任意一个数x,对应到B中唯一确定的数.
反比例函数:的定义域为,对应关系为“倒数的k倍”,值域为.反比例函数用函数定义叙述为:对于非空数集中的任意一个x值,按照对应关系f:“倒数倍”,在集合中都有唯一确定的数和它对应,那么此时f:就是集合A到集合B的一个函数,记作
探究二:函数的应用
例1
函数的解析式是舍弃问题的实际背景而抽象出来的,它所反映的两个量之间的对应关系,可以广泛地用于刻画一类事物中的变量关系和规律.
例如,正比例函数可以用来刻画匀速运动中路程与时间的关系、一定密度的物体的质量与体积的关系、圆的周长与半径的关系等.
试构建一个问题情境,使其中的变量关系可以用解析式来描述.
解:把看成二次函数,那么它的定义域是R,值域是.对应关系f把R中的任意一个数x,对应到B中唯一确定的数x(10-x).
如果对x的取值范围作出限制,例如,那么可以构建如下情境:
长方形的周长为20,设一边长为x,面积为y,那么y=x(10-x).
其中,x的取值范围是,y的取值范围是.对应关系f把每一个长方形的边长x,对应到唯一确定的面积x(10-x).
探究:构建其他可用解析式y=x(10-x)描述其中变量关系的问题情境.
答案:设两个实数的和为10,其中一个数为x,这两个数的积为y,则y=x(10-x),其
中x的取值范围为A=R,y的取值范围为.对应关系f把A中任一x值对应B中唯一确定的x(10-x).
探究三:区间
定义:研究函数时常会用到区间的概念.设a,b是两个实数,而且a
满足不等式的实数x的集合叫做闭区间,表示为[a,b];
(2)
满足不等式a
满足不等式或的实数x的集合叫做半开半闭区间,外别表示为[a,b),(a,b].这里的实数a与b都叫做相应区间的端点.
这些区间的几何表示如下表所示.在数轴表示时,用实心点表示包括在区间内的端点,用空心点表示不包括在区间内的端点.
实数集R可以用区间表示为,“”读作“无穷大”,“
”读作“负无穷大”,“
”读作“正无穷大”.
如下表,我们可以把满足的实数x的集合,用区间分别表示为
[a,+∞),(a,+∞),(-∞,b],(-∞,b).
表示区间应注意的问题:
(1)关注“开”与“闭”,“开”用小括号,“闭”用中括号;在数轴上,用实心点表示包括在区间内的端点,用空心点表示不包括在区间内的端点.
(2)区间实质上是一类特殊数集的另一种表示.并不是所有的数的集合都能用区间表示,如{0,1,2}就不能用区间表示.
(3)区间的左端点必须小于右端点,有时我们将b-a称为区间(a,b)或[a,b]的长度.
(4)用“-∞”或“+∞”作为区间端点时,需用开区间符号.
探究四:函数的定义域
例1.已知函数.
(1)求函数的定义域;
(2)求,的值.
答案:(1)使根式有意义的实数x的集合是,使分式有意义的实数x的集合是,所以函数的定义域是.
(2).
.
总结:
(1)当一个函数由两个或两个以上代数式的和、差、积、商的形式构成时,定义域是使各式子都有意义的公共部分的集合.
求函数定义域的步骤:
①列不等式(组):根据解析式有意义的条件,列出关于自变量的不等式(组)
②解不等式(组):解出所列不等式或不等式组中每个不等式的解集后在求交集
③得定义域:把不等式(组)的解集表示成集合或区间的形式
(2)已知函数解析式求函数值,可将自变量的值代入解析式求出相应的函数值.当自变量的值为包含字母的代数式时,将代数式作为一个整体代入求解.
探究五:相同函数
函数相同的条件:对应关系相同;定义域相同.
例1.判断下列各组中的两个函数是不是相同的函数.
(1),;
(2),.
答案:(1)的定义域为,而的定义域为两个函数的定义域不同,所以不是相同的函数.
(2)的定义域为,而的定义域为,两个函数的定义域不同,所以两个函数不是相同的函数.
(二)课堂练习
1.下列各图中,可表示函数的图象的是(
)
A.
B.
C.
D.
答案:D
解析:由函数的定义可知,对定义域内的任意一个变量x,都存在唯一确定的函数值y与之对应.A中,当时,有两个y与x对应;B中,当时,有两个y与x对应;C中,当时,有两个y与x对应;D中,对任意x都只有唯一确定的y与之对应.故选D.
2.不等式的解集用区间表示为(
)
A.
B.
C.
D.
答案:D
解析:由得,用区间表示为.故选D.
3.若周长为定值a的矩形,它的面积S是这个矩形的一边长x的函数,则这个函数的定义域是(
)
A.
B.
C.
D.
答案:D
解析:依题意知,矩形的一边长为x,则该边的邻边长为,由得,故这个函数的定义域是.故选D.
(三)小结作业
小结:
1.本节课我们主要学习了哪些内容?
2.函数的定义
3.函数三要素
4.区间
5.相同函数
作业:
四、板书设计
3.1.1函数的概念
1.函数的定义
2.函数三要素:定义域,对应关系,值域.
3.区间
4.相同函数:定义域,对应关系相同
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
