《探究弹性势能的表达式》教学设计
文档属性
| 名称 | 《探究弹性势能的表达式》教学设计 |

|
|
| 格式 | zip | ||
| 文件大小 | 217.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2012-06-13 00:00:00 | ||
图片预览



文档简介
探究弹性势能的表达式教学设计
参赛选手:王剑琴
指导老师:朱喜香
怀化学院物理与信息工程系,湖南怀化,418008
【教材分析】
“探究弹性势能的表达式”是人教版高中物理必修2第七章机械能守恒定律第五节内容。
在重力势能的基础上,将能量的形式迁移到弹性形变物体,是重力做功与重力势能关系的延伸,通过对弹性物体弹性势能表达式的探讨,加深了学生对能量转化和守恒的理解和认识,为后续的功能原理、机械能守恒定律奠定基础,对学生的知识和认知结构的建构起到了桥梁作用。
科学探究是有利于学生“构建知识”、形成“科学观念”、领悟“科学研究方法”的各种活动。本设计是以探究决定弹性势能大小的因素为载体,设计了实验探究和理论探究两种方案,两者相结合,让学生同时体验实验的魅力和类比创新思维的力量,并且通过科学探究培养学生的科学探究能力、实事求是的科学态度和敢于创新的精神。教材的安排体现了新课程理念。
本节课是探究弹性势能的表达式,因此,本堂课的教学重点之一是加深学生对科学探究活动的理解,突出学生主体,注重学生对规律建立过程的理解,掌握方法。让学生最大限度地参与到教学之中,充分发挥学生的积极性、主动性和创造性,提高学生的学习兴趣和科学探究的热情。
通过猜想和实验探究弹簧劲度系数、形变量与弹性势能的关系;通过弹簧弹力与弹性形变之间的关系和匀变速直线运动中速度与时间的数学类比,进行知识迁移,得到弹性势能的表达式,把微元极限思想和类比策略渗透到学生的思维是另一个教学重点。
【学情分析】
思维特点
科学探究既是学生的学习目标,又是重要的教学方式之一。通过初中课程的学习,学生对能量和功有了初步认识,对科学探究的过程有了一定的体验,并具备了一定的科学探究能力。
根据新课程教学理念,从高中物理必修一的教材内容安排,相当多的探究课题体现了“过程与方法”目标,学生具有一定的设计实验并动手操作的能力,具有较好的思考与质疑、交流与合作的学习习惯。因此,本设计通过创设问题情境,通过师生互动引导学生交流、讨论,提出猜想、确定探究目标和方案,通过实验合作探究,观察、分析实验现象,验证假设,发挥学生的主体作用,增强学生的学习积极性,培养类比思维和逻辑推理能力。
(2)心理特点
高一学生的认知发展过程是由具体运算阶段向形式运算阶段过渡,也是由直观认识向逻辑推理、实验论证过渡的阶段,他们喜欢探究事物的本质,敢于大胆发表自己的见解。因此在教学中,要遵循从感性到理性的认知规律,提供学生丰富而又具体的问题情境,充分满足与引导学生的好奇心,让学生自己主动提出问题,学会科学地分析和解决问题;针对高中学生认知发展不足,在学习过程中教授方法,培养他们良好的思维品质,使其克服思维发展中的主观性、片面性,促进思维全面深刻发展。
(3)知识基础
通过上一节《重力势能》的学习,学生已经初步体验到“研究重力势能是从重力做功入手”以及“功是能量转化的量度”,并且学生已具有一定知识迁移能力。因此可以让学生通过类比,从弹簧弹力对其它物体做功入手来研究弹簧弹性势能,根据高中学生已具有能量守恒思想,把对不能直接测量的弹性势能转化为对摩擦力做功大小的研究,这样可以让学生通过探究实验定量地得出影响弹性势能大小的因素。创设弹簧弹力与弹性形变之间的关系和匀变速直线运动中速度与时间的数学图像相似情境,类比得出弹性势能的表达式。
【教学目标】
一、知识与技能:
理解弹性势能的概念及影响弹性势能大小的因素;理解弹力做功与弹簧弹性势能的关系;
2、通过实验探究培养学生的观察能力、实验操作能力和交流合作能力;通过理论探究培养学生的创新思维能力。
二、过程与方法:
1、使学生经历探究过程,掌握实验探究的过程和方法,发展自主学习能力;
2、理解微元极限思想和类比方法。
三、情感态度与价值观:
1、通过探究活动,培养学生对科学的好奇心与求知欲,培养学生与他人合作的团队精神;
2、通过体会生活中能量转化的现象,培养学生的能量意识。
【教学重点和难点】
重点:1、通过探究弹性势能表达式,掌握科学探究的过程和方法;
2、体会微元极限思想和类比策略在物理学中的应用;
难点:1、理解实验原理;
2、设计探究方案;
3、实验数据的处理。
【教学设备】
弹簧若干,小车两辆,木板一块,教师演示用多媒体及其课件(PPT)
【教学流程】
【教学内容与过程】
教学环节 教学内容 教师活动 学生活动 设计意图
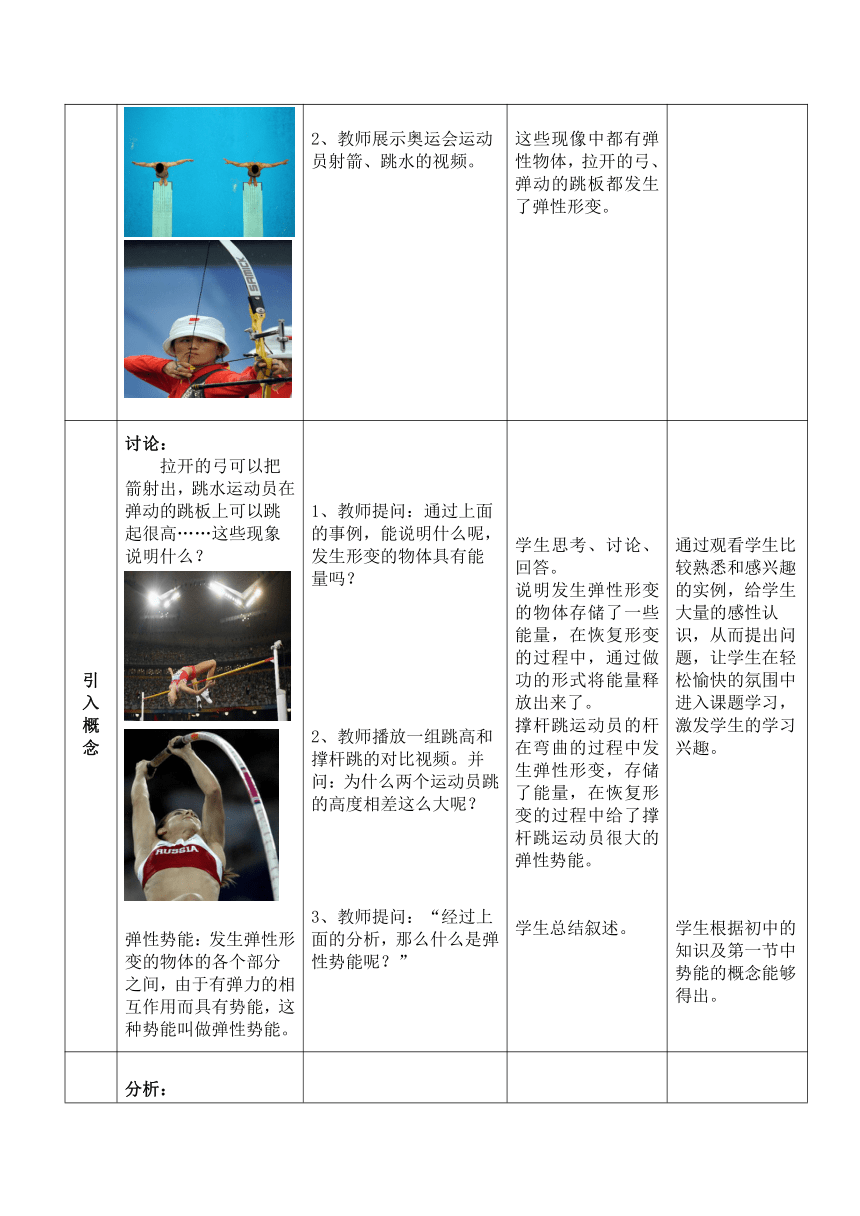
导入新课 思考:播放奥运会运动员射箭、跳水的视频,提问这些场景都有什么样的共同点呢? 1、教师提问:大家应该都观看2008年的北京奥运会,现在我们来回顾一下其中几个比赛项目的视频。注意观察,这些场景都有什么样的共同点呢?2、教师展示奥运会运动员射箭、跳水的视频。 学生观看视频,思考回答。这些现像中都有弹性物体,拉开的弓、弹动的跳板都发生了弹性形变。 引发学生思考,从生活走向物理,调动学习的积极性。
引入概念 讨论:拉开的弓可以把箭射出,跳水运动员在弹动的跳板上可以跳起很高……这些现象说明什么? 弹性势能:发生弹性形变的物体的各个部分之间,由于有弹力的相互作用而具有势能,这种势能叫做弹性势能。 1、教师提问:通过上面的事例,能说明什么呢,发生形变的物体具有能量吗?2、教师播放一组跳高和撑杆跳的对比视频。并问:为什么两个运动员跳的高度相差这么大呢?3、教师提问:“经过上面的分析,那么什么是弹性势能呢?” 学生思考、讨论、回答。说明发生弹性形变的物体存储了一些能量,在恢复形变的过程中,通过做功的形式将能量释放出来了。撑杆跳运动员的杆在弯曲的过程中发生弹性形变,存储了能量,在恢复形变的过程中给了撑杆跳运动员很大的弹性势能。学生总结叙述。 通过观看学生比较熟悉和感兴趣的实例,给学生大量的感性认识,从而提出问题,让学生在轻松愉快的氛围中进入课题学习,激发学生的学习兴趣。学生根据初中的知识及第一节中势能的概念能够得出。
定性分析 分析:1、物体形变量越大,弹性势能越大;2、弹性势能越大,对外做的功越多。 1、教师引导:我们重点来看下面这个运动,运动员在蹦床的过程中,为什么能从静止开始越跳越高呢?2、教师播放蹦床运动视频。 学生讨论,回答。运动员在跳的过程中,使床发生形变,用的力越大,形变量越大,所获得的弹性势能越大。床在恢复形变的过程中,所释放出来的弹性势能也越大,运动员就跳得越高。 引导学生通过具体的实例对弹性势能进行定性分析,能加深学生对弹性势能的认识,调动他们探究的积极性。
猜想假设 猜想:影响弹簧弹性势能大小的因素,可能与弹簧的形变量Δl、弹簧的劲度系数K有关。 1、给学生展示各种不同的弹簧,让他们观察。2、提问:结合上面的分析以及对手中的弹簧的观察,请大家猜想弹簧的弹性势能大小可能与什么因素有关?3、同学们说明了弹簧的弹性势能与弹簧形变量和劲度系数之间有关系,如何计算弹簧发生形变而具有的弹性势能多少呢 今天我们就来探究弹性势能的表达式。 学生思考、讨论、交流。猜想弹簧的弹性势能可能与弹簧拉伸或压缩的长度有关,还有可能与弹簧本身有关。学生讨论、交流。学生可能猜测为kΔl2或者其它。 培养学生的观察分析能力。鼓励学生进一步思考,充分调动他们的思维,一步一步朝目标靠近。
定量探究︵实验探究︶ 根据初中时学过的能量守恒定律,可以得出下面的实验中当小车静止时,弹簧给小车的能量等于摩擦力做功所消耗的能量。所以可通过摩擦力做功来研究弹簧的弹性势能。通过转换思想,把对不能直接测出的弹性势能的研究转换成了对内能的研究。通过控制变量的思想,(1)保持K一定,研究形变量Δl与Ep的关系。用同一个弹簧,不同的压缩量;(2)控制弹簧的压缩量Δl不变,研究K与Ep的关系,选取劲度系数不同的弹簧进行实验。(假设弹簧处于原长时,弹簧的弹性势能为零)通过交流讨论,分析作图可以得到: Ep∝k、Ep∝Δl2 。 教师指出:光有猜测还不够,要得到定量的关系,需要进行严格的分析和计算。每组同学桌上有劲度系数不同的弹簧,有小车,有可固定弹簧的木板。利用这些器材如何设计简单实验,探究弹簧弹性势能的大小与形变量和劲度系数之间的关系? 1、提问:通过小车怎样来比较弹簧的弹性势能大小?2、依据的原理是什么?3、教师提示:前面我们猜想了,弹性势能可能与弹簧的形变量大小、劲度系数有关,如果我们能够分别验证摩擦力做的功与弹簧的形变量Δl、劲度系数k之间的关系,那也就验证了Ep与这两者的定量关系了,这里我们可以运用以前学过的控制变量法。实验分三步走:(1)探究Ep与Δl的定量关系;(2)探究Ep与k的定量关系;(3)综合得出Ep与k、Δl的关系。做完后把数据填入到表格中(表附后)。4、教师提问:从得出的数据中我们可以发现什么规律呢?5、教师引导:由得到的结论我们可以猜想弹性势能的表达式为:Ep=AkΔl2,那么A等于多少呢,我们通过理论来探究。 1、学生讨论、交流。放一小车或木块,压缩弹簧后释放,让弹簧把它推出。2、压缩越大,小车运动得越远,可以通过比较小车运动的距离来比较弹簧压缩时所具有的弹性势能的大小。3、学生明确:从摩擦力做功入手研究弹簧的弹性势能。小车在运动过程中只有摩擦力做功,W=fS,根据能量守恒定律,弹簧的弹性势能最终都转化为了摩擦力做功。所以可以通过比较小车运动的距离来测量弹簧的弹性势能。3、学生四人一组进行讨论,设计实验。用小车压缩弹簧,释放,小车运动一段位移之后静止。(1)保持K一定,研究形变量Δl与Ep的关系。用同一个弹簧,不同的压缩量;(2)控制弹簧的压缩量不变,研究K与Ep的关系,选取劲度系数不同的弹簧进行实验。记录数据后填入表格内,并作出相应的图像。4、学生通过对表格内数据和图像的分析,可以得出,在实验误差范围内:Ep∝k、Ep∝Δl2 。 给出探究的目标,让学生进行定向探究,教师起着引导而不是代替的作用。让学生理解功是能量转化的量度,并通过自己设计实验来验证自己所猜想的结果,能激起学生的兴趣和激情。突破难点,突出重点。通过分组讨论并合作做出实验,培养了他们的团结协作能力,并让他们认识到在学习中相互帮助相互配合是很重要的。引导学生利用控制变量法定量探究弹性势能的决定因素,强化了他们对这一方法的认识,由他们自己得出的结论将使他们的理解更深刻。培养了学生的实验操作能力、逻辑思维能力,及数学方法在物理中的运用能力。
类比得到弹性势能的表达式︵理论探究︶ 创设弹簧弹力与弹性形变的关系和匀变速直线运动中速度与时间关系的情境,进行类比得到弹性势能的表达式。类比:匀变速直线运动中速度与时间的关系和弹簧弹力与形变量之间关系类比。利用微元法,把变力做功问题转化为恒力做功问题。(通过v-t图像进行知识迁移,引导学生利用F-t图像下的面积代表功。)最终可得到弹簧弹力做功的表达式Ep=kΔl2/2。 1、教师提问:上面我们猜想了弹性势能的表达式为Ep=AkΔl2,大家回忆一下,在我们前面学过的知识中,有没有一个公式的表达式和它是类似的?2、教师提示:弹力与匀变速直线运动中的速度相似,都是变化的,无法直接求出它们的大小。提问:在匀变速直线运动中我们是怎么解决这个问题的呢,它的公式是通过什么样的方法得出来的呢?3、引导学生回忆并类比研究匀变速直线运动位移的方法。4、教师提出:通过以上分析和类比,我们能否也通过图象法与微元法得出变力的功呢?5、教师鼓励点拨:“同学们运用了知识迁移法,那么下面我们该如何求各个小段做功之和?”6、教师适当引导:利用F-l图像下的面积来代表功。 学生回忆得到描述匀变速直线运动位移的公式s=at2/2与它相似。学生讨论:“可以利用微元法,把变力功问题转化为恒力功问题来解决。把拉伸的过程分为很多小段,它们的长度是Δl1、Δl2、Δl3……在各个小段上,拉力可以近似认为是不变的,它们分别是F1、F2、F3……所以,在各个小段上,拉力做的功分别是F1Δl1、F2Δl2、F3Δl3……拉力在整个过程中做的功可以用它在各个小段做功之和来表示F1Δl1+F2Δl2+F3Δl3……,”学生讨论提出作F-l图像。最后得出结论,弹性势能的表达式为:Ep=kΔl2/2 。 1、引导学生去思考,让他们通过前面学过的知识来联想解决后面的问题,学会学以致用。2、通过类比的方法化难为易,巩固学生已有的知识,把研究对象条理化,扩展学生的知识视野,从而提高学生分析问题、解决问题的思维能力,同时还能培养学生知识迁移能力和创新思维能力。3、通过分析计算,培养学生在物理中运用数学知识和方法的能力。4、让学生体会微积分思想和极限思想,研究变力做功,从而突破了重难点。5、由他们自己得出结论,可使他们理解得更透彻,体验到成功的快乐。
验证 由弹性势能的表达式Ep=kΔl2/2,说明在探究中,猜想与探究的结论是一致的,弹簧的弹性势能只与弹簧的形变量和劲度系数有关。 教师提示:“通过弹性势能的表达式Ep=kΔl2/2,说明弹簧的弹性势能与哪些因素有关?” 学生:“说明弹簧的弹性势能只与形变量和劲度系数有关,与猜想相一致。” 让学生体会探究方法,实验探究结果与逻辑推理结果的一致性。
总结 谈本节课的收获。 教师倾听、适当提示。引导学生重点总结本节课中运用的学科思想方法(如控制变量法、类比法、微元法、图像法等。)和探究的过程与方法(如猜想与假设、设计方案、实验验证或逻辑推理等)。 学生总结。 让学生知道通过本堂课的学习,运用到了很多科学探究的方法,同时让他们意识到在本堂课的探究中自己发挥了很大的作用,从而产生一种学习的成就感。
课外探究 讨论:在假设弹簧处于原长弹性势能为零的前提下,拉伸量为l时弹性势能的表达式是否还是:Ep=kΔl2/2 。 教师提问:刚才我们研究的是弹簧压缩的情形,拉伸的情形会是怎样的? 课后开展小组讨论探究。 培养学生思维的严密性,拓展学生的思维能力和激发他们的团结协作精神。
【板书设计】
探究弹性势能的表达式
1、定义:
发生弹性形变的物体的各个部分之间,由于有弹力的相互作用而具有势能,这种势能叫做弹性势能。
2、探究:
(1)问题:弹性势能的表达式是什么?
(2)猜想:影响弹性势能大小的因素:K、Δl
(3)设计实验:探究弹性势能的大小与K、Δl的定量关系。
(4)交流讨论:EP∝K EP∝Δl2
(5)类比:匀变速直线运动位移的求法,研究弹性势能。
(6)结论:
附表一:
保持弹簧的劲度系数K一定,研究形变量Δl与弹性势能的关系。
S Δl Δl2
1
2
3
4
坐标1:弹性势能与形变量的关系图:
表二:控制弹簧的压缩量Δl不变,研究劲度系数K与弹性势能的关系
K1 K2
S1
S2
S3
S4
坐标二:弹性势能与劲度系数的关系图
视频导入
定性分析
类比
方案设计
总结收获
定量探究
引出概念
实验探究
猜想假设
验证猜想
得到结论
提出问题
交流讨论
课外探究
o
t
v
o
t
v
o
t
v
o
l
F
o
l
F
o
l
F
物
理
量
次
数
s
△l2
0
劲
度
系数数
位
移
0
K1
K2
参赛选手:王剑琴
指导老师:朱喜香
怀化学院物理与信息工程系,湖南怀化,418008
【教材分析】
“探究弹性势能的表达式”是人教版高中物理必修2第七章机械能守恒定律第五节内容。
在重力势能的基础上,将能量的形式迁移到弹性形变物体,是重力做功与重力势能关系的延伸,通过对弹性物体弹性势能表达式的探讨,加深了学生对能量转化和守恒的理解和认识,为后续的功能原理、机械能守恒定律奠定基础,对学生的知识和认知结构的建构起到了桥梁作用。
科学探究是有利于学生“构建知识”、形成“科学观念”、领悟“科学研究方法”的各种活动。本设计是以探究决定弹性势能大小的因素为载体,设计了实验探究和理论探究两种方案,两者相结合,让学生同时体验实验的魅力和类比创新思维的力量,并且通过科学探究培养学生的科学探究能力、实事求是的科学态度和敢于创新的精神。教材的安排体现了新课程理念。
本节课是探究弹性势能的表达式,因此,本堂课的教学重点之一是加深学生对科学探究活动的理解,突出学生主体,注重学生对规律建立过程的理解,掌握方法。让学生最大限度地参与到教学之中,充分发挥学生的积极性、主动性和创造性,提高学生的学习兴趣和科学探究的热情。
通过猜想和实验探究弹簧劲度系数、形变量与弹性势能的关系;通过弹簧弹力与弹性形变之间的关系和匀变速直线运动中速度与时间的数学类比,进行知识迁移,得到弹性势能的表达式,把微元极限思想和类比策略渗透到学生的思维是另一个教学重点。
【学情分析】
思维特点
科学探究既是学生的学习目标,又是重要的教学方式之一。通过初中课程的学习,学生对能量和功有了初步认识,对科学探究的过程有了一定的体验,并具备了一定的科学探究能力。
根据新课程教学理念,从高中物理必修一的教材内容安排,相当多的探究课题体现了“过程与方法”目标,学生具有一定的设计实验并动手操作的能力,具有较好的思考与质疑、交流与合作的学习习惯。因此,本设计通过创设问题情境,通过师生互动引导学生交流、讨论,提出猜想、确定探究目标和方案,通过实验合作探究,观察、分析实验现象,验证假设,发挥学生的主体作用,增强学生的学习积极性,培养类比思维和逻辑推理能力。
(2)心理特点
高一学生的认知发展过程是由具体运算阶段向形式运算阶段过渡,也是由直观认识向逻辑推理、实验论证过渡的阶段,他们喜欢探究事物的本质,敢于大胆发表自己的见解。因此在教学中,要遵循从感性到理性的认知规律,提供学生丰富而又具体的问题情境,充分满足与引导学生的好奇心,让学生自己主动提出问题,学会科学地分析和解决问题;针对高中学生认知发展不足,在学习过程中教授方法,培养他们良好的思维品质,使其克服思维发展中的主观性、片面性,促进思维全面深刻发展。
(3)知识基础
通过上一节《重力势能》的学习,学生已经初步体验到“研究重力势能是从重力做功入手”以及“功是能量转化的量度”,并且学生已具有一定知识迁移能力。因此可以让学生通过类比,从弹簧弹力对其它物体做功入手来研究弹簧弹性势能,根据高中学生已具有能量守恒思想,把对不能直接测量的弹性势能转化为对摩擦力做功大小的研究,这样可以让学生通过探究实验定量地得出影响弹性势能大小的因素。创设弹簧弹力与弹性形变之间的关系和匀变速直线运动中速度与时间的数学图像相似情境,类比得出弹性势能的表达式。
【教学目标】
一、知识与技能:
理解弹性势能的概念及影响弹性势能大小的因素;理解弹力做功与弹簧弹性势能的关系;
2、通过实验探究培养学生的观察能力、实验操作能力和交流合作能力;通过理论探究培养学生的创新思维能力。
二、过程与方法:
1、使学生经历探究过程,掌握实验探究的过程和方法,发展自主学习能力;
2、理解微元极限思想和类比方法。
三、情感态度与价值观:
1、通过探究活动,培养学生对科学的好奇心与求知欲,培养学生与他人合作的团队精神;
2、通过体会生活中能量转化的现象,培养学生的能量意识。
【教学重点和难点】
重点:1、通过探究弹性势能表达式,掌握科学探究的过程和方法;
2、体会微元极限思想和类比策略在物理学中的应用;
难点:1、理解实验原理;
2、设计探究方案;
3、实验数据的处理。
【教学设备】
弹簧若干,小车两辆,木板一块,教师演示用多媒体及其课件(PPT)
【教学流程】
【教学内容与过程】
教学环节 教学内容 教师活动 学生活动 设计意图
导入新课 思考:播放奥运会运动员射箭、跳水的视频,提问这些场景都有什么样的共同点呢? 1、教师提问:大家应该都观看2008年的北京奥运会,现在我们来回顾一下其中几个比赛项目的视频。注意观察,这些场景都有什么样的共同点呢?2、教师展示奥运会运动员射箭、跳水的视频。 学生观看视频,思考回答。这些现像中都有弹性物体,拉开的弓、弹动的跳板都发生了弹性形变。 引发学生思考,从生活走向物理,调动学习的积极性。
引入概念 讨论:拉开的弓可以把箭射出,跳水运动员在弹动的跳板上可以跳起很高……这些现象说明什么? 弹性势能:发生弹性形变的物体的各个部分之间,由于有弹力的相互作用而具有势能,这种势能叫做弹性势能。 1、教师提问:通过上面的事例,能说明什么呢,发生形变的物体具有能量吗?2、教师播放一组跳高和撑杆跳的对比视频。并问:为什么两个运动员跳的高度相差这么大呢?3、教师提问:“经过上面的分析,那么什么是弹性势能呢?” 学生思考、讨论、回答。说明发生弹性形变的物体存储了一些能量,在恢复形变的过程中,通过做功的形式将能量释放出来了。撑杆跳运动员的杆在弯曲的过程中发生弹性形变,存储了能量,在恢复形变的过程中给了撑杆跳运动员很大的弹性势能。学生总结叙述。 通过观看学生比较熟悉和感兴趣的实例,给学生大量的感性认识,从而提出问题,让学生在轻松愉快的氛围中进入课题学习,激发学生的学习兴趣。学生根据初中的知识及第一节中势能的概念能够得出。
定性分析 分析:1、物体形变量越大,弹性势能越大;2、弹性势能越大,对外做的功越多。 1、教师引导:我们重点来看下面这个运动,运动员在蹦床的过程中,为什么能从静止开始越跳越高呢?2、教师播放蹦床运动视频。 学生讨论,回答。运动员在跳的过程中,使床发生形变,用的力越大,形变量越大,所获得的弹性势能越大。床在恢复形变的过程中,所释放出来的弹性势能也越大,运动员就跳得越高。 引导学生通过具体的实例对弹性势能进行定性分析,能加深学生对弹性势能的认识,调动他们探究的积极性。
猜想假设 猜想:影响弹簧弹性势能大小的因素,可能与弹簧的形变量Δl、弹簧的劲度系数K有关。 1、给学生展示各种不同的弹簧,让他们观察。2、提问:结合上面的分析以及对手中的弹簧的观察,请大家猜想弹簧的弹性势能大小可能与什么因素有关?3、同学们说明了弹簧的弹性势能与弹簧形变量和劲度系数之间有关系,如何计算弹簧发生形变而具有的弹性势能多少呢 今天我们就来探究弹性势能的表达式。 学生思考、讨论、交流。猜想弹簧的弹性势能可能与弹簧拉伸或压缩的长度有关,还有可能与弹簧本身有关。学生讨论、交流。学生可能猜测为kΔl2或者其它。 培养学生的观察分析能力。鼓励学生进一步思考,充分调动他们的思维,一步一步朝目标靠近。
定量探究︵实验探究︶ 根据初中时学过的能量守恒定律,可以得出下面的实验中当小车静止时,弹簧给小车的能量等于摩擦力做功所消耗的能量。所以可通过摩擦力做功来研究弹簧的弹性势能。通过转换思想,把对不能直接测出的弹性势能的研究转换成了对内能的研究。通过控制变量的思想,(1)保持K一定,研究形变量Δl与Ep的关系。用同一个弹簧,不同的压缩量;(2)控制弹簧的压缩量Δl不变,研究K与Ep的关系,选取劲度系数不同的弹簧进行实验。(假设弹簧处于原长时,弹簧的弹性势能为零)通过交流讨论,分析作图可以得到: Ep∝k、Ep∝Δl2 。 教师指出:光有猜测还不够,要得到定量的关系,需要进行严格的分析和计算。每组同学桌上有劲度系数不同的弹簧,有小车,有可固定弹簧的木板。利用这些器材如何设计简单实验,探究弹簧弹性势能的大小与形变量和劲度系数之间的关系? 1、提问:通过小车怎样来比较弹簧的弹性势能大小?2、依据的原理是什么?3、教师提示:前面我们猜想了,弹性势能可能与弹簧的形变量大小、劲度系数有关,如果我们能够分别验证摩擦力做的功与弹簧的形变量Δl、劲度系数k之间的关系,那也就验证了Ep与这两者的定量关系了,这里我们可以运用以前学过的控制变量法。实验分三步走:(1)探究Ep与Δl的定量关系;(2)探究Ep与k的定量关系;(3)综合得出Ep与k、Δl的关系。做完后把数据填入到表格中(表附后)。4、教师提问:从得出的数据中我们可以发现什么规律呢?5、教师引导:由得到的结论我们可以猜想弹性势能的表达式为:Ep=AkΔl2,那么A等于多少呢,我们通过理论来探究。 1、学生讨论、交流。放一小车或木块,压缩弹簧后释放,让弹簧把它推出。2、压缩越大,小车运动得越远,可以通过比较小车运动的距离来比较弹簧压缩时所具有的弹性势能的大小。3、学生明确:从摩擦力做功入手研究弹簧的弹性势能。小车在运动过程中只有摩擦力做功,W=fS,根据能量守恒定律,弹簧的弹性势能最终都转化为了摩擦力做功。所以可以通过比较小车运动的距离来测量弹簧的弹性势能。3、学生四人一组进行讨论,设计实验。用小车压缩弹簧,释放,小车运动一段位移之后静止。(1)保持K一定,研究形变量Δl与Ep的关系。用同一个弹簧,不同的压缩量;(2)控制弹簧的压缩量不变,研究K与Ep的关系,选取劲度系数不同的弹簧进行实验。记录数据后填入表格内,并作出相应的图像。4、学生通过对表格内数据和图像的分析,可以得出,在实验误差范围内:Ep∝k、Ep∝Δl2 。 给出探究的目标,让学生进行定向探究,教师起着引导而不是代替的作用。让学生理解功是能量转化的量度,并通过自己设计实验来验证自己所猜想的结果,能激起学生的兴趣和激情。突破难点,突出重点。通过分组讨论并合作做出实验,培养了他们的团结协作能力,并让他们认识到在学习中相互帮助相互配合是很重要的。引导学生利用控制变量法定量探究弹性势能的决定因素,强化了他们对这一方法的认识,由他们自己得出的结论将使他们的理解更深刻。培养了学生的实验操作能力、逻辑思维能力,及数学方法在物理中的运用能力。
类比得到弹性势能的表达式︵理论探究︶ 创设弹簧弹力与弹性形变的关系和匀变速直线运动中速度与时间关系的情境,进行类比得到弹性势能的表达式。类比:匀变速直线运动中速度与时间的关系和弹簧弹力与形变量之间关系类比。利用微元法,把变力做功问题转化为恒力做功问题。(通过v-t图像进行知识迁移,引导学生利用F-t图像下的面积代表功。)最终可得到弹簧弹力做功的表达式Ep=kΔl2/2。 1、教师提问:上面我们猜想了弹性势能的表达式为Ep=AkΔl2,大家回忆一下,在我们前面学过的知识中,有没有一个公式的表达式和它是类似的?2、教师提示:弹力与匀变速直线运动中的速度相似,都是变化的,无法直接求出它们的大小。提问:在匀变速直线运动中我们是怎么解决这个问题的呢,它的公式是通过什么样的方法得出来的呢?3、引导学生回忆并类比研究匀变速直线运动位移的方法。4、教师提出:通过以上分析和类比,我们能否也通过图象法与微元法得出变力的功呢?5、教师鼓励点拨:“同学们运用了知识迁移法,那么下面我们该如何求各个小段做功之和?”6、教师适当引导:利用F-l图像下的面积来代表功。 学生回忆得到描述匀变速直线运动位移的公式s=at2/2与它相似。学生讨论:“可以利用微元法,把变力功问题转化为恒力功问题来解决。把拉伸的过程分为很多小段,它们的长度是Δl1、Δl2、Δl3……在各个小段上,拉力可以近似认为是不变的,它们分别是F1、F2、F3……所以,在各个小段上,拉力做的功分别是F1Δl1、F2Δl2、F3Δl3……拉力在整个过程中做的功可以用它在各个小段做功之和来表示F1Δl1+F2Δl2+F3Δl3……,”学生讨论提出作F-l图像。最后得出结论,弹性势能的表达式为:Ep=kΔl2/2 。 1、引导学生去思考,让他们通过前面学过的知识来联想解决后面的问题,学会学以致用。2、通过类比的方法化难为易,巩固学生已有的知识,把研究对象条理化,扩展学生的知识视野,从而提高学生分析问题、解决问题的思维能力,同时还能培养学生知识迁移能力和创新思维能力。3、通过分析计算,培养学生在物理中运用数学知识和方法的能力。4、让学生体会微积分思想和极限思想,研究变力做功,从而突破了重难点。5、由他们自己得出结论,可使他们理解得更透彻,体验到成功的快乐。
验证 由弹性势能的表达式Ep=kΔl2/2,说明在探究中,猜想与探究的结论是一致的,弹簧的弹性势能只与弹簧的形变量和劲度系数有关。 教师提示:“通过弹性势能的表达式Ep=kΔl2/2,说明弹簧的弹性势能与哪些因素有关?” 学生:“说明弹簧的弹性势能只与形变量和劲度系数有关,与猜想相一致。” 让学生体会探究方法,实验探究结果与逻辑推理结果的一致性。
总结 谈本节课的收获。 教师倾听、适当提示。引导学生重点总结本节课中运用的学科思想方法(如控制变量法、类比法、微元法、图像法等。)和探究的过程与方法(如猜想与假设、设计方案、实验验证或逻辑推理等)。 学生总结。 让学生知道通过本堂课的学习,运用到了很多科学探究的方法,同时让他们意识到在本堂课的探究中自己发挥了很大的作用,从而产生一种学习的成就感。
课外探究 讨论:在假设弹簧处于原长弹性势能为零的前提下,拉伸量为l时弹性势能的表达式是否还是:Ep=kΔl2/2 。 教师提问:刚才我们研究的是弹簧压缩的情形,拉伸的情形会是怎样的? 课后开展小组讨论探究。 培养学生思维的严密性,拓展学生的思维能力和激发他们的团结协作精神。
【板书设计】
探究弹性势能的表达式
1、定义:
发生弹性形变的物体的各个部分之间,由于有弹力的相互作用而具有势能,这种势能叫做弹性势能。
2、探究:
(1)问题:弹性势能的表达式是什么?
(2)猜想:影响弹性势能大小的因素:K、Δl
(3)设计实验:探究弹性势能的大小与K、Δl的定量关系。
(4)交流讨论:EP∝K EP∝Δl2
(5)类比:匀变速直线运动位移的求法,研究弹性势能。
(6)结论:
附表一:
保持弹簧的劲度系数K一定,研究形变量Δl与弹性势能的关系。
S Δl Δl2
1
2
3
4
坐标1:弹性势能与形变量的关系图:
表二:控制弹簧的压缩量Δl不变,研究劲度系数K与弹性势能的关系
K1 K2
S1
S2
S3
S4
坐标二:弹性势能与劲度系数的关系图
视频导入
定性分析
类比
方案设计
总结收获
定量探究
引出概念
实验探究
猜想假设
验证猜想
得到结论
提出问题
交流讨论
课外探究
o
t
v
o
t
v
o
t
v
o
l
F
o
l
F
o
l
F
物
理
量
次
数
s
△l2
0
劲
度
系数数
位
移
0
K1
K2
