4.1 指数 课件(共15张PPT)
文档属性
| 名称 | 4.1 指数 课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-28 15:55:11 | ||
图片预览






文档简介
(共15张PPT)
人教版A版(2019)
必修第一册
4.1
指数
1.理解n次方根及根式的概念,掌握根式的性质.
2.掌握指数幂的运算性质.
3.体会数学抽象的过程,加强逻辑推理、数学运算素养的培养.
1.a的n次方根的定义
一般地,如果①????xn=a????,那么x叫做a的n次方根,其中n>1,且n∈N
.
2.a的n次方根的表示
n的奇偶性
a的n次方根的表示符号
a的取值范围
n为奇数
?
R
n为偶数
②????±?????
[0,+∞)
根式
(3)?=0.
(4)负数没有偶次方根.
3.根式
式子?叫做根式,这里n叫做③ 根指数????,a叫做被开方数.
4.根式的性质(其中n>1,且n∈N
)?
(1)n为奇数时,?=a.
(2)n为偶数时,?=|a|=④?????????.
?
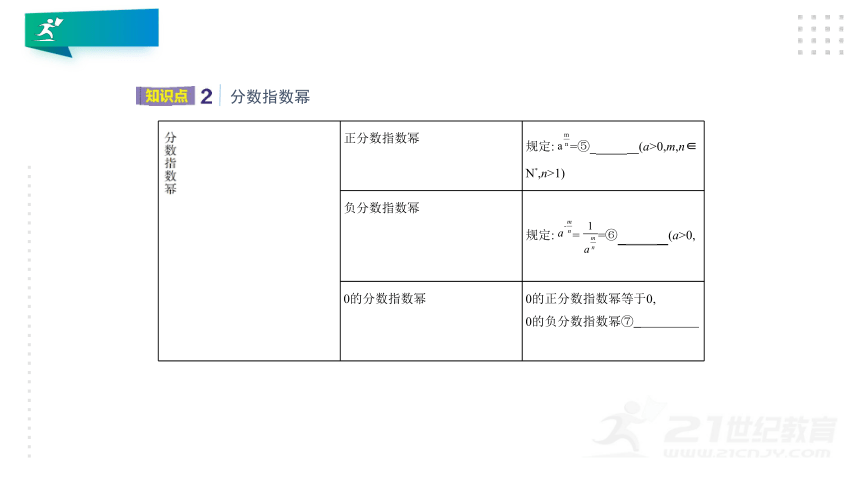
正分数指数幂
规定:?=⑤?????????(a>0,m,n∈
N
,n>1)
负分数指数幂
规定:?=?=⑥ ? (a>0,
0的分数指数幂
0的正分数指数幂等于0,
0的负分数指数幂⑦ 没有意义
分数指数幂
(1)aras=?(a>0,r,s∈Q);
(2)(ar)s=⑧????ars????(a>0,r,s∈Q);
(3)(ab)r=⑨????arbr????(a>0,b>0,r∈Q).
有理数指数幂的运算性质
无理数指数幂
一般地,无理数指数幂aα(a>0,α为无理数)是一个确定的⑩ 实数????.有理数指
数幂的运算性质同样适用于无理数指数幂.
1.实数a的奇次方根有且只有一个.?( √ )
2.任何实数都有偶次方根.?(????? )
3.0的任意次方根都为0.?( √ )
4.(?)n中实数a的取值范围是任意实数.?(????? )
提示:当n为大于1的奇数时,a∈R;当n为大于1的偶数时,a≥0.
5.分数指数幂与根式可以相互转化,如?=?.?(????? )
提示:?=?
6.a2·?=a.?(????? )
提示:a2·?=?=?.
判断正误,正确的画“√”
,错误的画“
?”
.
根式与分数指数幂的化简与计算
?利用根式的性质进行根式化简与求值,解题的思路及注意点
1.思路:首先要分清根式为奇次根式还是偶次根式,然后运用根式的性质进行化简.
2.注意点:
(1)根式性质的适用范围:n为奇数时,(?)n=?=a,a为任意实数;n为偶数,a≥0时,
(?)n才有意义,且(?)n=a;n为偶数,a为任意实数时,?均有意义,且?=|a|.
(2)运算时注意变式、整体代换,以及平方差公式、立方差公式、完全平方公式、
完全立方公式的运用,必要时要进行分类讨论.
?
1.指数幂运算的原则与技巧
(1)有括号先算括号里的,无括号先进行指数幂的运算.
(2)负指数幂化为正指数幂的倒数.
(3)底数是小数的,要先化成分数;底数是带分数的,要先化成假分数,然后要尽可能
?
1.指数幂运算的原则与技巧
(1)有括号先算括号里的,无括号先进行指数幂的运算.
(2)负指数幂化为正指数幂的倒数.
(3)底数是小数的,要先化成分数;底数是带分数的,要先化成假分数,然后要尽可能
用幂的形式表示,便于利用指数幂的运算性质.
注意:化简的结果不能同时含有根式和分数指数,也不能既含有分母又含有负指数.
2.解决条件求值问题的一般方法——整体代入法
对于条件求值问题,一般先化简代数式,再将字母的值代入并求值.但有时字母的取
值未知或不易求出,这时可将所求代数式进行恰当地变形,构造出与已知条件相同
的结构,从而通过“整体代入法”求出代数式的值.利用“整体代入法”求值时常
用的变形公式如下:
(1)a±2??+b=(?±?)2;
(2)(?+?)(?-?)=a-b;
(3)?+?=(?+?)(a-??+b);
(4)?-?=(?-?)(a+??+b).
??
计算:(1)?+?-?;
(2)?×?(a>0,b>0).
思路点拨
利用指数幂的运算性质计算,将含有根式的先化成分数指数幂,再计算.
解析????(1)原式=(?)2+?-?=0.09+?-?=0.09.
(2)原式=?·?·?·?·?=?a0b0=?.
导师点睛????进行指数幂运算时,化负指数为正指数,化根式为分数指数幂,化小数为
分数,化带分数为假分数,便于进行乘、除、乘方、开方运算,以达到化繁为简的目
的.
??
已知?+?=?,求下列各式的值:
(1)a2+a-2;(2)?.
思路点拨
寻找要求值的式子与已知条件?+?=?的联系,进而整体代入求值.
解析????(1)将?+?=?两边平方,得a+a-1+2=7,
所以a+a-1=5,
再将a+a-1=5两边平方,得a2+a-2+2=25,
故a2+a-2=23.
(2)由(1)得a+a-1=5.
因为?-?=(?)3-(?)3,
所以原式=?
=a+a-1+1=5+1=6.
https://www.21cnjy.com/help/help_extract.php
人教版A版(2019)
必修第一册
4.1
指数
1.理解n次方根及根式的概念,掌握根式的性质.
2.掌握指数幂的运算性质.
3.体会数学抽象的过程,加强逻辑推理、数学运算素养的培养.
1.a的n次方根的定义
一般地,如果①????xn=a????,那么x叫做a的n次方根,其中n>1,且n∈N
.
2.a的n次方根的表示
n的奇偶性
a的n次方根的表示符号
a的取值范围
n为奇数
?
R
n为偶数
②????±?????
[0,+∞)
根式
(3)?=0.
(4)负数没有偶次方根.
3.根式
式子?叫做根式,这里n叫做③ 根指数????,a叫做被开方数.
4.根式的性质(其中n>1,且n∈N
)?
(1)n为奇数时,?=a.
(2)n为偶数时,?=|a|=④?????????.
?
正分数指数幂
规定:?=⑤?????????(a>0,m,n∈
N
,n>1)
负分数指数幂
规定:?=?=⑥ ? (a>0,
0的分数指数幂
0的正分数指数幂等于0,
0的负分数指数幂⑦ 没有意义
分数指数幂
(1)aras=?(a>0,r,s∈Q);
(2)(ar)s=⑧????ars????(a>0,r,s∈Q);
(3)(ab)r=⑨????arbr????(a>0,b>0,r∈Q).
有理数指数幂的运算性质
无理数指数幂
一般地,无理数指数幂aα(a>0,α为无理数)是一个确定的⑩ 实数????.有理数指
数幂的运算性质同样适用于无理数指数幂.
1.实数a的奇次方根有且只有一个.?( √ )
2.任何实数都有偶次方根.?(????? )
3.0的任意次方根都为0.?( √ )
4.(?)n中实数a的取值范围是任意实数.?(????? )
提示:当n为大于1的奇数时,a∈R;当n为大于1的偶数时,a≥0.
5.分数指数幂与根式可以相互转化,如?=?.?(????? )
提示:?=?
6.a2·?=a.?(????? )
提示:a2·?=?=?.
判断正误,正确的画“√”
,错误的画“
?”
.
根式与分数指数幂的化简与计算
?利用根式的性质进行根式化简与求值,解题的思路及注意点
1.思路:首先要分清根式为奇次根式还是偶次根式,然后运用根式的性质进行化简.
2.注意点:
(1)根式性质的适用范围:n为奇数时,(?)n=?=a,a为任意实数;n为偶数,a≥0时,
(?)n才有意义,且(?)n=a;n为偶数,a为任意实数时,?均有意义,且?=|a|.
(2)运算时注意变式、整体代换,以及平方差公式、立方差公式、完全平方公式、
完全立方公式的运用,必要时要进行分类讨论.
?
1.指数幂运算的原则与技巧
(1)有括号先算括号里的,无括号先进行指数幂的运算.
(2)负指数幂化为正指数幂的倒数.
(3)底数是小数的,要先化成分数;底数是带分数的,要先化成假分数,然后要尽可能
?
1.指数幂运算的原则与技巧
(1)有括号先算括号里的,无括号先进行指数幂的运算.
(2)负指数幂化为正指数幂的倒数.
(3)底数是小数的,要先化成分数;底数是带分数的,要先化成假分数,然后要尽可能
用幂的形式表示,便于利用指数幂的运算性质.
注意:化简的结果不能同时含有根式和分数指数,也不能既含有分母又含有负指数.
2.解决条件求值问题的一般方法——整体代入法
对于条件求值问题,一般先化简代数式,再将字母的值代入并求值.但有时字母的取
值未知或不易求出,这时可将所求代数式进行恰当地变形,构造出与已知条件相同
的结构,从而通过“整体代入法”求出代数式的值.利用“整体代入法”求值时常
用的变形公式如下:
(1)a±2??+b=(?±?)2;
(2)(?+?)(?-?)=a-b;
(3)?+?=(?+?)(a-??+b);
(4)?-?=(?-?)(a+??+b).
??
计算:(1)?+?-?;
(2)?×?(a>0,b>0).
思路点拨
利用指数幂的运算性质计算,将含有根式的先化成分数指数幂,再计算.
解析????(1)原式=(?)2+?-?=0.09+?-?=0.09.
(2)原式=?·?·?·?·?=?a0b0=?.
导师点睛????进行指数幂运算时,化负指数为正指数,化根式为分数指数幂,化小数为
分数,化带分数为假分数,便于进行乘、除、乘方、开方运算,以达到化繁为简的目
的.
??
已知?+?=?,求下列各式的值:
(1)a2+a-2;(2)?.
思路点拨
寻找要求值的式子与已知条件?+?=?的联系,进而整体代入求值.
解析????(1)将?+?=?两边平方,得a+a-1+2=7,
所以a+a-1=5,
再将a+a-1=5两边平方,得a2+a-2+2=25,
故a2+a-2=23.
(2)由(1)得a+a-1=5.
因为?-?=(?)3-(?)3,
所以原式=?
=a+a-1+1=5+1=6.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
