4.4.3不同函数增长的差异 课件(共17张PPT)
文档属性
| 名称 | 4.4.3不同函数增长的差异 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-28 16:49:32 | ||
图片预览






文档简介
(共17张PPT)
人教版A版(2019)
必修第一册
4.4.3 不同函数增长的差异
学习本节内容,体会常见函数的变化异同,提升数学建模、数据分析的能力.要注意
以下几点:
1.掌握常见增长函数的定义、图象、性质,并体会其增长速度的差异.
2.理解直线上升、对数增长、指数爆炸的含义以及三种函数模型的比较.
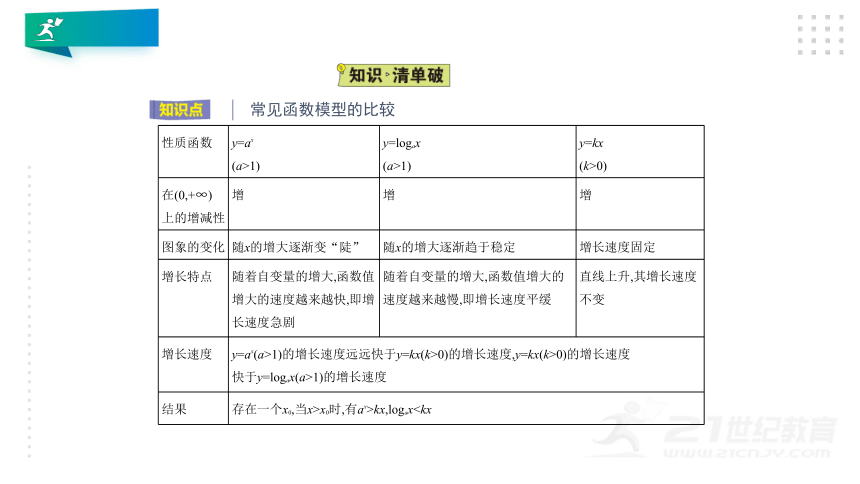
性质函数
y=ax
(a>1)
y=logax
(a>1)
y=kx
(k>0)
在(0,+∞)
上的增减性
增
增
增
图象的变化
随x的增大逐渐变“陡”
随x的增大逐渐趋于稳定
增长速度固定
增长特点
随着自变量的增大,函数值增大的速度越来越快,即增长速度急剧
随着自变量的增大,函数值增大的速度越来越慢,即增长速度平缓
直线上升,其增长速度
不变
增长速度
y=ax(a>1)的增长速度远远快于y=kx(k>0)的增长速度,y=kx(k>0)的增长速度
快于y=logax(a>1)的增长速度
结果
存在一个x0,当x>x0时,有ax>kx,logax常见函数模型的比较
1.
函数y=x2比y=2x增长的速度更快些.?(????? )
2.函数y=logax(a>1)和幂函数y=xn(n>0)在区间(0,+∞)上,总存在一个x0,当x>x0时,logax
提示:根据图象可知结论正确.
3.在函数y=3x,y=log3x,y=3x,y=x3中,增长速度最快的是y=3x.?( √ )
提示:在这几类函数中,指数函数的增长速度最快.
4.当0判断正误,正确的画“√”
,错误的画“
?”
.
几类函数模型的增长差异的比较
假如某公司每天向你投资1万元,共投资30天.该公司要求你给他的回报是第一
天给公司1分钱,第二天给公司2分钱,以后每天给的钱都是前一天的2倍,共30天.
问题
1.你认为这样的交易对你有利吗?
提示:公司30天内给你的总投资为30万元(一次函数模型);
你30天内给公司的回报为
0.01+0.01×2+0.01×22+…+0.01×229=10
737
418.23≈1
07
4(万元)(指数函数模型).
由此可见,这样的交易对你没有利.
2.上述问题中,你发现了什么问题?
提示:函数y=ax(a>1)与y=kx(k>0)都是增函数,随着x的增大,指数函数的增长速度越
来越快,相比指数函数,一次函数增长得较慢.
?常见的函数模型及增长特点
1.线性函数模型y=kx+b(k>0)的增长特点是直线上升,其增长速度不变.
2.指数函数模型y=ax(a>1)的增长特点是随着自变量的增大,函数值增大的速度越来
越快,即增长速度急剧,形象地称为“指数爆炸”.
3.对数函数模型y=logax(a>1)的增长特点是随着自变量的增大,函数值增大的速度
越来越慢,即增长速度平缓.
??
甲、乙、丙、丁四个物体同时从某一点出发向同一个方向运动,其路程fi(x)(i=
1,2,3,4)关于时间x(x≥0)的函数关系式分别为f1(x)=2x-1,
f2(x)=x2,
f3(x)=x,
f4(x)=log2(x
+1),有以下结论:
①当x>1时,甲在最前面;
②当x>1时,乙在最前面;
③当01时,丁在最后面;
④丙不可能在最前面,也不可能在最后面;
⑤如果它们一直运动下去,那么最终在最前面的是甲.
其中,正确结论的序号为 ????.
思路点拨
确定函数的类型,在同一坐标系中作出各函数图象,比较各个函数的变化趋势.
解析????路程fi(x)(i=1,2,3,4)关于时间x(x≥0)的函数关系式分别为f1(x)=2x-1,
f2(x)=x2,
f
3(x)=x,
f4(x)=log2(x+1),
它们相对应的函数模型分别是指数型函数、二次函数、一次函数和对数型函数.
当x=2时,
f1(2)=3,
f2(2)=4,∴①不正确;
当x=5时,
f1(5)=31,
f2(5)=25,∴②不正确;
根据四种函数的变化特点,对数型函数的增长速度是先快后慢,画出四个函数的图
象(图略),可知当x=1时,甲、乙、丙、丁四个物体的路程相等,从而当0最前面,当x>1时,丁在最后面,∴③正确;
结合对数型函数和指数型函数的图象变化情况,可知丙不可能在最前面,也不可能
在最后面,∴④正确;
指数函数的增长速度是先慢后快,若运动的时间足够长,则最前面的物体一定是按
照指数型函数运动的物体,即一定是甲,∴⑤正确.
答案 ③④⑤
?不同的函数模型能刻画现实世界中不同的变化规律
(1)线性函数增长模型适合描述增长速度不变的变化规律;
(2)指数型函数增长模型适合描述增长速度急剧的变化规律;
(3)对数型函数增长模型适合描述增长速度平缓的变化规律;
(4)幂函数型增长模型适合描述增长速度一般的变化规律.
因此,需抓住题中蕴含的数学信息,恰当、准确地建立相应变化规律的函数模型来
解决实际问题.
几种常见的函数模型的选择
??
某皮鞋厂今年1月份开始投产,并且前4个月的产量分别为1万双,1.2万双,1.3万
双,1.37万双.由于产品质量好、款式新颖,前几个月的销售情况良好.为了推销员在
推销产品时接受订单不至于过多或过少,需要估计以后几个月的产量,且厂里暂时
不准备增加设备和工人.假如你是厂长,就月份为x,产量为y给出三种函数模型:y=ax
+b,y=ax2+bx+c,y=abx+c,其中a≠0,你将利用哪一种模型去估算以后几个月的产量?
思路点拨
结合函数模型的增长速度选择合适的模型求解.
解析????由题意知,将产量随时间变化的离散量分别抽象为A(1,1),B(2,1.2),C(3,1.3),D
(4,1.37)4个点.
(1)令模拟函数为y=ax+b,
将B,C两点的坐标代入函数解析式,
得?解得?∴y=0.1x+1.
由此可得结论:在不增加工人和设备的条件下,产量会每月增加1
000双,这是不太
可能的.
(2)令模拟函数为y=ax2+bx+c,将A,B,C三点的坐标代入函数解析式,
得?解得?
∴y=-0.05x2+0.35x+0.7.
由此得出结论:由此式计算得4月份的产量为1.3万双,比实际产量少700双,而且由
二次函数的性质可知,产量自4月份开始每月下降(图象开口向下,对称轴为x=3.5),
不符合实际.
(3)令模拟函数为y=abx+c,
将A,B,C三点的坐标代入函数解析式,
得?
由①得ab=1-c,代入②③,
得?则?解得?
则a=?=-0.8,
∴y=-0.8×0.5x+1.4.
由此得出结论:把x=4代入,得y=-0.8×0.54+1.4=1.35.
比较上述三个模拟函数的优劣时,既要考虑误差最小,又要考虑生产的实际,如:增
产的趋势和可能性.经过筛选,以y=-0.8×0.5x+1.4模拟为最佳,一是误差小,二是由于
厂房新建,随着工人技术和管理效益逐渐提高,一段时间内产量会明显上升,但经过
一段时间之后,如果不增加设备和工人,产量必然趋于稳定,而y=-0.8×0.5x+1.4恰好
反映了这种趋势.
因此选用指数型函数y=-0.8×0.5x+1.4模拟比较接近客观实际.
https://www.21cnjy.com/help/help_extract.php
人教版A版(2019)
必修第一册
4.4.3 不同函数增长的差异
学习本节内容,体会常见函数的变化异同,提升数学建模、数据分析的能力.要注意
以下几点:
1.掌握常见增长函数的定义、图象、性质,并体会其增长速度的差异.
2.理解直线上升、对数增长、指数爆炸的含义以及三种函数模型的比较.
性质函数
y=ax
(a>1)
y=logax
(a>1)
y=kx
(k>0)
在(0,+∞)
上的增减性
增
增
增
图象的变化
随x的增大逐渐变“陡”
随x的增大逐渐趋于稳定
增长速度固定
增长特点
随着自变量的增大,函数值增大的速度越来越快,即增长速度急剧
随着自变量的增大,函数值增大的速度越来越慢,即增长速度平缓
直线上升,其增长速度
不变
增长速度
y=ax(a>1)的增长速度远远快于y=kx(k>0)的增长速度,y=kx(k>0)的增长速度
快于y=logax(a>1)的增长速度
结果
存在一个x0,当x>x0时,有ax>kx,logax
1.
函数y=x2比y=2x增长的速度更快些.?(????? )
2.函数y=logax(a>1)和幂函数y=xn(n>0)在区间(0,+∞)上,总存在一个x0,当x>x0时,logax
3.在函数y=3x,y=log3x,y=3x,y=x3中,增长速度最快的是y=3x.?( √ )
提示:在这几类函数中,指数函数的增长速度最快.
4.当0
,错误的画“
?”
.
几类函数模型的增长差异的比较
假如某公司每天向你投资1万元,共投资30天.该公司要求你给他的回报是第一
天给公司1分钱,第二天给公司2分钱,以后每天给的钱都是前一天的2倍,共30天.
问题
1.你认为这样的交易对你有利吗?
提示:公司30天内给你的总投资为30万元(一次函数模型);
你30天内给公司的回报为
0.01+0.01×2+0.01×22+…+0.01×229=10
737
418.23≈1
07
4(万元)(指数函数模型).
由此可见,这样的交易对你没有利.
2.上述问题中,你发现了什么问题?
提示:函数y=ax(a>1)与y=kx(k>0)都是增函数,随着x的增大,指数函数的增长速度越
来越快,相比指数函数,一次函数增长得较慢.
?常见的函数模型及增长特点
1.线性函数模型y=kx+b(k>0)的增长特点是直线上升,其增长速度不变.
2.指数函数模型y=ax(a>1)的增长特点是随着自变量的增大,函数值增大的速度越来
越快,即增长速度急剧,形象地称为“指数爆炸”.
3.对数函数模型y=logax(a>1)的增长特点是随着自变量的增大,函数值增大的速度
越来越慢,即增长速度平缓.
??
甲、乙、丙、丁四个物体同时从某一点出发向同一个方向运动,其路程fi(x)(i=
1,2,3,4)关于时间x(x≥0)的函数关系式分别为f1(x)=2x-1,
f2(x)=x2,
f3(x)=x,
f4(x)=log2(x
+1),有以下结论:
①当x>1时,甲在最前面;
②当x>1时,乙在最前面;
③当0
④丙不可能在最前面,也不可能在最后面;
⑤如果它们一直运动下去,那么最终在最前面的是甲.
其中,正确结论的序号为 ????.
思路点拨
确定函数的类型,在同一坐标系中作出各函数图象,比较各个函数的变化趋势.
解析????路程fi(x)(i=1,2,3,4)关于时间x(x≥0)的函数关系式分别为f1(x)=2x-1,
f2(x)=x2,
f
3(x)=x,
f4(x)=log2(x+1),
它们相对应的函数模型分别是指数型函数、二次函数、一次函数和对数型函数.
当x=2时,
f1(2)=3,
f2(2)=4,∴①不正确;
当x=5时,
f1(5)=31,
f2(5)=25,∴②不正确;
根据四种函数的变化特点,对数型函数的增长速度是先快后慢,画出四个函数的图
象(图略),可知当x=1时,甲、乙、丙、丁四个物体的路程相等,从而当0
结合对数型函数和指数型函数的图象变化情况,可知丙不可能在最前面,也不可能
在最后面,∴④正确;
指数函数的增长速度是先慢后快,若运动的时间足够长,则最前面的物体一定是按
照指数型函数运动的物体,即一定是甲,∴⑤正确.
答案 ③④⑤
?不同的函数模型能刻画现实世界中不同的变化规律
(1)线性函数增长模型适合描述增长速度不变的变化规律;
(2)指数型函数增长模型适合描述增长速度急剧的变化规律;
(3)对数型函数增长模型适合描述增长速度平缓的变化规律;
(4)幂函数型增长模型适合描述增长速度一般的变化规律.
因此,需抓住题中蕴含的数学信息,恰当、准确地建立相应变化规律的函数模型来
解决实际问题.
几种常见的函数模型的选择
??
某皮鞋厂今年1月份开始投产,并且前4个月的产量分别为1万双,1.2万双,1.3万
双,1.37万双.由于产品质量好、款式新颖,前几个月的销售情况良好.为了推销员在
推销产品时接受订单不至于过多或过少,需要估计以后几个月的产量,且厂里暂时
不准备增加设备和工人.假如你是厂长,就月份为x,产量为y给出三种函数模型:y=ax
+b,y=ax2+bx+c,y=abx+c,其中a≠0,你将利用哪一种模型去估算以后几个月的产量?
思路点拨
结合函数模型的增长速度选择合适的模型求解.
解析????由题意知,将产量随时间变化的离散量分别抽象为A(1,1),B(2,1.2),C(3,1.3),D
(4,1.37)4个点.
(1)令模拟函数为y=ax+b,
将B,C两点的坐标代入函数解析式,
得?解得?∴y=0.1x+1.
由此可得结论:在不增加工人和设备的条件下,产量会每月增加1
000双,这是不太
可能的.
(2)令模拟函数为y=ax2+bx+c,将A,B,C三点的坐标代入函数解析式,
得?解得?
∴y=-0.05x2+0.35x+0.7.
由此得出结论:由此式计算得4月份的产量为1.3万双,比实际产量少700双,而且由
二次函数的性质可知,产量自4月份开始每月下降(图象开口向下,对称轴为x=3.5),
不符合实际.
(3)令模拟函数为y=abx+c,
将A,B,C三点的坐标代入函数解析式,
得?
由①得ab=1-c,代入②③,
得?则?解得?
则a=?=-0.8,
∴y=-0.8×0.5x+1.4.
由此得出结论:把x=4代入,得y=-0.8×0.54+1.4=1.35.
比较上述三个模拟函数的优劣时,既要考虑误差最小,又要考虑生产的实际,如:增
产的趋势和可能性.经过筛选,以y=-0.8×0.5x+1.4模拟为最佳,一是误差小,二是由于
厂房新建,随着工人技术和管理效益逐渐提高,一段时间内产量会明显上升,但经过
一段时间之后,如果不增加设备和工人,产量必然趋于稳定,而y=-0.8×0.5x+1.4恰好
反映了这种趋势.
因此选用指数型函数y=-0.8×0.5x+1.4模拟比较接近客观实际.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
