4.5.1-4.5.2 函数的零点与方程的解 用二分法求方程的近似解 课件(共27张PPT)
文档属性
| 名称 | 4.5.1-4.5.2 函数的零点与方程的解 用二分法求方程的近似解 课件(共27张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-28 00:00:00 | ||
图片预览








文档简介
(共27张PPT)
人教版A版(2019)
必修第一册
4.5
函数的应用(二)
4.5.1 函数的零点与方程的解
4.5.2 用二分法求方程的近似解
1.结合学过的函数图象,了解函数的零点与方程解的关系.
2.结合具体连续函数及其图象的特点,了解函数零点存在定理.
3.能借助计算工具用二分法求方程的近似解.
1.函数的零点的概念
对于函数y=f(x),我们把使①????f(x)=0????的实数x叫做函数y=f(x)的零点.
2.方程、函数、图象之间的关系
方程f(x)=0有实数解?函数y=f(x)② 有零点?????函数y=f(x)的图象与x轴有公共点.
3.函数的零点的本质是方程f(x)=0的实数解,因此,函数的零点不是点,而是一个实
数.
函数的零点
如果函数y=f(x)在区间[a,b]上的图象是一条③ 连续不断????的曲线,且有
④????f(a)f(b)<0
,那么,函数y=f(x)在区间(a,b)内至少有一个零点,即存在c∈(a,b),使得⑤????f(c)=0????,这个
c也就是方程f(x)=0的解.
函数零点存在定理
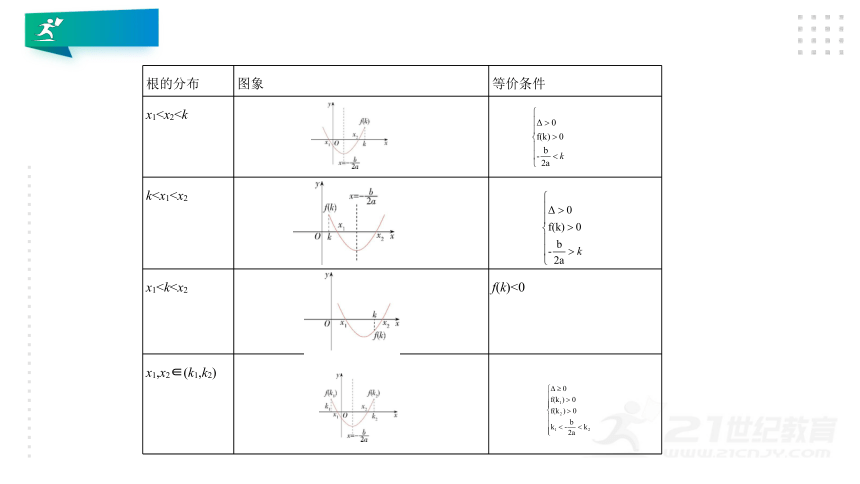
设x1,x2是实系数一元二次方程ax2+bx+c=0
(a>0)的两个实数根,则x1,x2的分布范
围与一元二次方程系数之间的关系如下表所示.
一元二次方程ax2+bx+c=0(a>0)根的分布问题
根的分布
图象
等价条件
x1?
?
k?
?
x1?
f(k)<0
x1,x2∈(k1,k2)
?
?
对于在区间[a,b]上图象连续不断且⑥????f(a)f(b)<0????的函数y=f(x),通过不断地
把它的零点所在区间⑦ 一分为二????,使所得区间的两个端点⑧ 逐步逼近零点,
进而得到零点近似值的方法叫做二分法.
二分法
给定精确度ε,用二分法求函数y=f(x)零点x0的近
似值的一般步骤如下:
1.确定零点x0的初始区间[a,b],验证⑨????f(a)f(b)<0????.
2.求区间(a,b)的中点c.
3.计算f(c),并进一步确定零点所在的区间:
(1)若f(c)=0(此时x0=c),则c就是函数的零点;
(2)若f(a)f(c)<0
(此时x0∈⑩ (a,c)????),则令b=c;
(3)若f(c)f(b)<0(此时x0∈? (c,b)????),则令a=c.
4.判断是否达到精确度ε:若|a-b|<ε,则得到零点近似值a(或b);否则重复步骤2~4.
用二分法求函数y=f(x)零点近似值的步骤
1.所有的函数都有零点.?(????? )
2.若方程f(x)=0有两个不相等的实数根x1,x2,则函数y=f(x)的零点为(x1,0),(x2,0).?
(????? )
3.若函数y=f(x)在区间(a,b)上有零点,则一定有f(a)·f(b)<0.?(????? )
4.函数y=2x-1的零点是?.?( √ )
5.用二分法可求所有函数的零点.?(????? )
6.用二分法求方程的近似解时,可以精确到小数点后的任一位.?( √ )
判断正误,正确的画“√”
,错误的画“
?”
.
求函数的零点
?
1.求函数f(x)的零点,通常转化为解方程f(x)=0.若方程f(x)=0有实数根,则函数f(x)存
在零点,该方程的根就是函数f(x)的零点;否则,函数f(x)不存在零点.
(1)对于二次函数的零点,可以用多种方法求解,如公式法、因式分解法、配方法.
(2)对于三次及三次以上的高次函数的零点,一般采用因式分解法求解.
(3)对于指数、对数函数的零点,一般是解指数、对数方程.
(4)对于不能用求根公式或分解因式求解的方程,可以将它与对应函数的图象联系
起来,利用函数的性质求零点.
2.确定函数零点所在区间的方法:确定函数的零点、方程的根所在的区间时,通常
利用函数零点存在定理,转化为判断区间两端点对应的函数值的符号是否相反.
求下列函数的零点:
(1)f(x)=(lg
x)2-lg
x;
(2)f(x)=x3-2x2-x+2.
思路点拨
分析函数对应的方程类型,
选择解决此类方程的方法,通过解方程得到函数的零点.
解析????(1)令(lg
x)2-lg
x=0,则lg
x(lg
x-1)=0,
∴lg
x=0或lg
x=1,∴x=1或x=10,
因此函数f(x)的零点是1,10.
(2)令x3-2x2-x+2=0,得x2(x-2)-(x-2)=(x-2)·(x2-1)=(x-2)(x+1)(x-1)=0,
解得x=-1或x=1或x=2,
∴函数f(x)有3个零点,分别为-1,1,2.
?
函数y=f(x)的零点就是方程f(x)=0的实数根,也就是函数y=f(x)的图象与x轴交点的横
坐标,所以函数的零点是一个数,而不是一个点.在写函数零点时,所写的一定是一个
数字,而不是一个坐标.
??
求函数f(x)=?的零点.
思路点拨
求函数零点,即求相应方程的根,解方程可得函数零点.
解析????当x≤0时,令x2+2x-3=0,解得x=-3或x=1(舍去);
当x>0时,令-2+ln
x=0,解得x=e2.
所以函数f(x)=?的零点为-3和e2.
函数零点个数的判断及应用
如果把函数比作一部电影,那么函数的零点就像电影的一个瞬间,一个镜头.有
时我们会忽略一些镜头,但是我们仍然能推测出被忽略的片段.现在有两组镜头(如
图,第一组为第一行两图,第二组为第二行两图).
?
问题
1.哪一组能说明他的行程中一定曾渡过河?
提示:第一组能说明他的行程中一定曾渡过河,而第二组中他的行程不一定曾渡过
河.
2.将河流抽象成x轴,将前后的两个位置视为A,B两点.请问:当A,B与x轴有怎样的位
置关系时,A,B间的一段连续不断的函数图象与x轴一定有交点?
提示:A,B两点在x轴的两侧.
?
1.判断函数f(x)的零点个数的主要方法:
(1)转化为解相应的方程,有几个根就有几个零点.
(2)画出函数y=f(x)的图象,判断它与x轴的交点个数,从而判断零点的个数.
(3)借助函数的单调性进行判断.若函数f(x)在区间[a,b]上的图象是一条连续不断的
曲线,且在区间(a,b)上单调,满足f(a)·f(b)<0,则函数f(x)在区间(a,b)上有且仅有一个
零点,如图所示.
?
(4)转化成两个函数图象的交点问题.
2.已知函数f(x)的零点个数求参数范围,为了便于限制零点个数或零点所在区间,通
常要对已知条件进行变形,变形的方向:(1)化为常见的基本初等函数;(2)尽量使参
数与变量分离,实在不能分离,也要使含参数的函数解析式尽可能简单.
??
求函数f(x)=2x+lg(x+1)-2的零点个数.
思路点拨
应用函数零点存在定理及单调性求解或将其转化为求两函数图象的交点个数,通
过数形结合进行求解.
解析????解法一:∵f(0)=1+0-2=-1<0,f(1)=2+lg
2-2>0,且f(x)在(0,1)上是连续的,
∴f(x)在(0,1)上必定存在零点.又f(x)=2x+lg(x+1)-2在(-1,+∞)上为增函数,
∴函数f(x)有且只有一个零点.
解法二:令h(x)=2-2x,g(x)=lg(x+1).在同一平面直角坐标系中作出h(x)和g(x)的草图如
图.
?
由图可知g(x)=lg(x+1)的图象和h(x)=2-2x的图象有且只有一个交点,即f(x)=2x+lg(x+
1)-2有且只有一个零点.
??
已知函数f(x)=|2x-2|-b有两个零点,求实数b的取值范围.
解析????令f(x)=|2x-2|-b=0,得|2x-2|=b.在同一平面直角坐标系中画出y=|2x-2|的图象与
直线y=b,如图所示.
?
由图可知当0b有两个零点.故实数b的取值范围是{b|0 在一档娱乐节目中,主持人让选手在规定时间内猜某物品的价格,若猜中了,就
把该物品作为奖励送给选手.某次竞猜的物品为价格在800~1
200元的一款手机,选
手开始报价.选手:“1
000.”主持人:“低了.”……
用二分法求函数零点的近似值
问题
1.如果是你,你知道接下来该如何竞猜吗?
提示:应猜1
000与1
200的中间值1
100.
2.通过这种方法能猜到具体价格吗?能用这种方法求方程的近似解吗?
提示:能猜到具体价格,能求方程的近似解.
3.用二分法求方程的近似解,如何决定步骤的结束?
提示:当零点所在区间的两个端点值之差的绝对值小于精确度时,二分法步骤结束.
4.用二分法求方程的近似解时,精确度不同对零点的近似值有影响吗?
提示:有影响.精确度决定步骤的始终,故精确度不同,零点的近似值可能会不同.
??
用二分法求函数f(x)=x3-3的零点的近似值(精确度为0.02).
思路点拨
估计函数零点所在初始区间,再用二分法的运算规则依次计算,得到精确度范围内
的区间时,取区间端点值或中点值(区间内的任意值均可)为近似值.
解析????由于f(0)=-3<0,
f(1)=-2<0,
f(2)=5>0,因此可取区间(1,2)作为计算的初始区间.
用二分法逐次计算,列表如下:
零点所在区间
中点的值
中点函数值
(或近似值)
(1,2)
1.5
0.375
(1,1.5)
1.25
-1.047
(1.25,1.5)
1.375
-0.400
(1.375,1.5)
1.437
5
-0.030
(1.437
5,1.5)
1.468
75
0.168
(1.437
5,1.468
75)
1.453
125
0.068
零点所在区间
中点的值
中点函数值
(或近似值)
(1.437
5,1.453
125)
1.445
312
5
0.019
续表
因为|1.453
125-1.437
5|=0.015
625<0.02,
所以函数f(x)=x3-3的零点的近似值可取为1.437
5.
??
在26枚崭新的金币中,混入了一枚外表与它们完全相同的假币(质量比真币的
略小).现只有一台天平,请问:利用二分法的思想,你至多几次就一定可以找出这枚
假币?
解析????利用二分法,至多四次就一定可以找出这枚假币.第一次把26枚金币平均分
成两组,放在天平两端,天平一定不平衡,轻的一组(13枚金币)含假币;第二次把含假
币的13枚金币分成三组:6,6,1,把有6枚金币的两组放在天平两端,如果平衡,那么剩
下的一枚是假币(称量结束),如果不平衡,那么轻的一组(6枚金币)含假币;第三次把
含假币的6枚金币分成两组,放在天平两端,天平不平衡,轻的一组(3枚金币)含假币;
第四次把含假币的3枚金币分成3组,1,1,1,取其中的两枚金币放在天平两端,如果平
衡,那么剩下的一枚是假币,如果不平衡,那么轻的一枚是假币.因此,最多四次就一
定可以找到假币.
解题模板
根据实际情况将被研究的对象进行适当分组,这是减少检验次数的要点,解题时要
灵活选择,采用最优的方法进行检验.
https://www.21cnjy.com/help/help_extract.php
人教版A版(2019)
必修第一册
4.5
函数的应用(二)
4.5.1 函数的零点与方程的解
4.5.2 用二分法求方程的近似解
1.结合学过的函数图象,了解函数的零点与方程解的关系.
2.结合具体连续函数及其图象的特点,了解函数零点存在定理.
3.能借助计算工具用二分法求方程的近似解.
1.函数的零点的概念
对于函数y=f(x),我们把使①????f(x)=0????的实数x叫做函数y=f(x)的零点.
2.方程、函数、图象之间的关系
方程f(x)=0有实数解?函数y=f(x)② 有零点?????函数y=f(x)的图象与x轴有公共点.
3.函数的零点的本质是方程f(x)=0的实数解,因此,函数的零点不是点,而是一个实
数.
函数的零点
如果函数y=f(x)在区间[a,b]上的图象是一条③ 连续不断????的曲线,且有
④????f(a)f(b)<0
,那么,函数y=f(x)在区间(a,b)内至少有一个零点,即存在c∈(a,b),使得⑤????f(c)=0????,这个
c也就是方程f(x)=0的解.
函数零点存在定理
设x1,x2是实系数一元二次方程ax2+bx+c=0
(a>0)的两个实数根,则x1,x2的分布范
围与一元二次方程系数之间的关系如下表所示.
一元二次方程ax2+bx+c=0(a>0)根的分布问题
根的分布
图象
等价条件
x1
?
k
?
x1
f(k)<0
x1,x2∈(k1,k2)
?
?
对于在区间[a,b]上图象连续不断且⑥????f(a)f(b)<0????的函数y=f(x),通过不断地
把它的零点所在区间⑦ 一分为二????,使所得区间的两个端点⑧ 逐步逼近零点,
进而得到零点近似值的方法叫做二分法.
二分法
给定精确度ε,用二分法求函数y=f(x)零点x0的近
似值的一般步骤如下:
1.确定零点x0的初始区间[a,b],验证⑨????f(a)f(b)<0????.
2.求区间(a,b)的中点c.
3.计算f(c),并进一步确定零点所在的区间:
(1)若f(c)=0(此时x0=c),则c就是函数的零点;
(2)若f(a)f(c)<0
(此时x0∈⑩ (a,c)????),则令b=c;
(3)若f(c)f(b)<0(此时x0∈? (c,b)????),则令a=c.
4.判断是否达到精确度ε:若|a-b|<ε,则得到零点近似值a(或b);否则重复步骤2~4.
用二分法求函数y=f(x)零点近似值的步骤
1.所有的函数都有零点.?(????? )
2.若方程f(x)=0有两个不相等的实数根x1,x2,则函数y=f(x)的零点为(x1,0),(x2,0).?
(????? )
3.若函数y=f(x)在区间(a,b)上有零点,则一定有f(a)·f(b)<0.?(????? )
4.函数y=2x-1的零点是?.?( √ )
5.用二分法可求所有函数的零点.?(????? )
6.用二分法求方程的近似解时,可以精确到小数点后的任一位.?( √ )
判断正误,正确的画“√”
,错误的画“
?”
.
求函数的零点
?
1.求函数f(x)的零点,通常转化为解方程f(x)=0.若方程f(x)=0有实数根,则函数f(x)存
在零点,该方程的根就是函数f(x)的零点;否则,函数f(x)不存在零点.
(1)对于二次函数的零点,可以用多种方法求解,如公式法、因式分解法、配方法.
(2)对于三次及三次以上的高次函数的零点,一般采用因式分解法求解.
(3)对于指数、对数函数的零点,一般是解指数、对数方程.
(4)对于不能用求根公式或分解因式求解的方程,可以将它与对应函数的图象联系
起来,利用函数的性质求零点.
2.确定函数零点所在区间的方法:确定函数的零点、方程的根所在的区间时,通常
利用函数零点存在定理,转化为判断区间两端点对应的函数值的符号是否相反.
求下列函数的零点:
(1)f(x)=(lg
x)2-lg
x;
(2)f(x)=x3-2x2-x+2.
思路点拨
分析函数对应的方程类型,
选择解决此类方程的方法,通过解方程得到函数的零点.
解析????(1)令(lg
x)2-lg
x=0,则lg
x(lg
x-1)=0,
∴lg
x=0或lg
x=1,∴x=1或x=10,
因此函数f(x)的零点是1,10.
(2)令x3-2x2-x+2=0,得x2(x-2)-(x-2)=(x-2)·(x2-1)=(x-2)(x+1)(x-1)=0,
解得x=-1或x=1或x=2,
∴函数f(x)有3个零点,分别为-1,1,2.
?
函数y=f(x)的零点就是方程f(x)=0的实数根,也就是函数y=f(x)的图象与x轴交点的横
坐标,所以函数的零点是一个数,而不是一个点.在写函数零点时,所写的一定是一个
数字,而不是一个坐标.
??
求函数f(x)=?的零点.
思路点拨
求函数零点,即求相应方程的根,解方程可得函数零点.
解析????当x≤0时,令x2+2x-3=0,解得x=-3或x=1(舍去);
当x>0时,令-2+ln
x=0,解得x=e2.
所以函数f(x)=?的零点为-3和e2.
函数零点个数的判断及应用
如果把函数比作一部电影,那么函数的零点就像电影的一个瞬间,一个镜头.有
时我们会忽略一些镜头,但是我们仍然能推测出被忽略的片段.现在有两组镜头(如
图,第一组为第一行两图,第二组为第二行两图).
?
问题
1.哪一组能说明他的行程中一定曾渡过河?
提示:第一组能说明他的行程中一定曾渡过河,而第二组中他的行程不一定曾渡过
河.
2.将河流抽象成x轴,将前后的两个位置视为A,B两点.请问:当A,B与x轴有怎样的位
置关系时,A,B间的一段连续不断的函数图象与x轴一定有交点?
提示:A,B两点在x轴的两侧.
?
1.判断函数f(x)的零点个数的主要方法:
(1)转化为解相应的方程,有几个根就有几个零点.
(2)画出函数y=f(x)的图象,判断它与x轴的交点个数,从而判断零点的个数.
(3)借助函数的单调性进行判断.若函数f(x)在区间[a,b]上的图象是一条连续不断的
曲线,且在区间(a,b)上单调,满足f(a)·f(b)<0,则函数f(x)在区间(a,b)上有且仅有一个
零点,如图所示.
?
(4)转化成两个函数图象的交点问题.
2.已知函数f(x)的零点个数求参数范围,为了便于限制零点个数或零点所在区间,通
常要对已知条件进行变形,变形的方向:(1)化为常见的基本初等函数;(2)尽量使参
数与变量分离,实在不能分离,也要使含参数的函数解析式尽可能简单.
??
求函数f(x)=2x+lg(x+1)-2的零点个数.
思路点拨
应用函数零点存在定理及单调性求解或将其转化为求两函数图象的交点个数,通
过数形结合进行求解.
解析????解法一:∵f(0)=1+0-2=-1<0,f(1)=2+lg
2-2>0,且f(x)在(0,1)上是连续的,
∴f(x)在(0,1)上必定存在零点.又f(x)=2x+lg(x+1)-2在(-1,+∞)上为增函数,
∴函数f(x)有且只有一个零点.
解法二:令h(x)=2-2x,g(x)=lg(x+1).在同一平面直角坐标系中作出h(x)和g(x)的草图如
图.
?
由图可知g(x)=lg(x+1)的图象和h(x)=2-2x的图象有且只有一个交点,即f(x)=2x+lg(x+
1)-2有且只有一个零点.
??
已知函数f(x)=|2x-2|-b有两个零点,求实数b的取值范围.
解析????令f(x)=|2x-2|-b=0,得|2x-2|=b.在同一平面直角坐标系中画出y=|2x-2|的图象与
直线y=b,如图所示.
?
由图可知当0
把该物品作为奖励送给选手.某次竞猜的物品为价格在800~1
200元的一款手机,选
手开始报价.选手:“1
000.”主持人:“低了.”……
用二分法求函数零点的近似值
问题
1.如果是你,你知道接下来该如何竞猜吗?
提示:应猜1
000与1
200的中间值1
100.
2.通过这种方法能猜到具体价格吗?能用这种方法求方程的近似解吗?
提示:能猜到具体价格,能求方程的近似解.
3.用二分法求方程的近似解,如何决定步骤的结束?
提示:当零点所在区间的两个端点值之差的绝对值小于精确度时,二分法步骤结束.
4.用二分法求方程的近似解时,精确度不同对零点的近似值有影响吗?
提示:有影响.精确度决定步骤的始终,故精确度不同,零点的近似值可能会不同.
??
用二分法求函数f(x)=x3-3的零点的近似值(精确度为0.02).
思路点拨
估计函数零点所在初始区间,再用二分法的运算规则依次计算,得到精确度范围内
的区间时,取区间端点值或中点值(区间内的任意值均可)为近似值.
解析????由于f(0)=-3<0,
f(1)=-2<0,
f(2)=5>0,因此可取区间(1,2)作为计算的初始区间.
用二分法逐次计算,列表如下:
零点所在区间
中点的值
中点函数值
(或近似值)
(1,2)
1.5
0.375
(1,1.5)
1.25
-1.047
(1.25,1.5)
1.375
-0.400
(1.375,1.5)
1.437
5
-0.030
(1.437
5,1.5)
1.468
75
0.168
(1.437
5,1.468
75)
1.453
125
0.068
零点所在区间
中点的值
中点函数值
(或近似值)
(1.437
5,1.453
125)
1.445
312
5
0.019
续表
因为|1.453
125-1.437
5|=0.015
625<0.02,
所以函数f(x)=x3-3的零点的近似值可取为1.437
5.
??
在26枚崭新的金币中,混入了一枚外表与它们完全相同的假币(质量比真币的
略小).现只有一台天平,请问:利用二分法的思想,你至多几次就一定可以找出这枚
假币?
解析????利用二分法,至多四次就一定可以找出这枚假币.第一次把26枚金币平均分
成两组,放在天平两端,天平一定不平衡,轻的一组(13枚金币)含假币;第二次把含假
币的13枚金币分成三组:6,6,1,把有6枚金币的两组放在天平两端,如果平衡,那么剩
下的一枚是假币(称量结束),如果不平衡,那么轻的一组(6枚金币)含假币;第三次把
含假币的6枚金币分成两组,放在天平两端,天平不平衡,轻的一组(3枚金币)含假币;
第四次把含假币的3枚金币分成3组,1,1,1,取其中的两枚金币放在天平两端,如果平
衡,那么剩下的一枚是假币,如果不平衡,那么轻的一枚是假币.因此,最多四次就一
定可以找到假币.
解题模板
根据实际情况将被研究的对象进行适当分组,这是减少检验次数的要点,解题时要
灵活选择,采用最优的方法进行检验.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
