4.5.3函数模型的应用 课件(共22张PPT)
文档属性
| 名称 | 4.5.3函数模型的应用 课件(共22张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-28 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
人教版A版(2019)
必修第一册
4.5.3 函数模型的应用
1.理解函数是描述客观世界中变量关系和规律的重要数学语言和工具.
2.在实际情境中,会选择合适的函数类型刻画现实问题的变化规律.
3.阅读、收集一些现实生活、实际生产或者经济领域中的数学模型,体会人们是如
何借助函数刻画实际问题的,感悟数学模型中参数的现实意义.
?
一次函数模型
y=kx+b(k,b为常数,k≠0)
二次函数模型
y=ax2+bx+c(a,b,c为常数,a≠0)
指数型函数模型
y=bax+c(a,b,c为常数,b≠0,a>0
且a≠1)
对数型函数模型
y=mlogax+n(m,a,n为常数,m≠
0,a>0且a≠1)
幂函数型模型
y=axn+b(a,n,b为常数,a≠0)
常见的函数模型
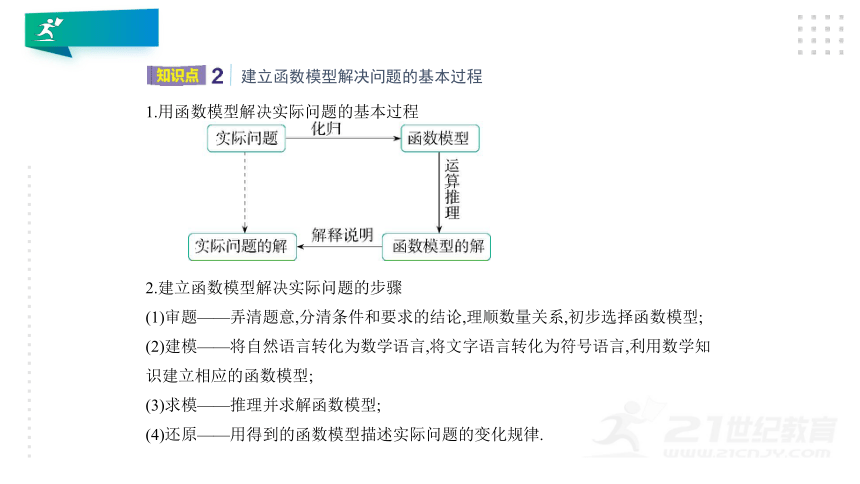
1.用函数模型解决实际问题的基本过程
2.建立函数模型解决实际问题的步骤
(1)审题——弄清题意,分清条件和要求的结论,理顺数量关系,初步选择函数模型;
(2)建模——将自然语言转化为数学语言,将文字语言转化为符号语言,利用数学知
识建立相应的函数模型;
(3)求模——推理并求解函数模型;
(4)还原——用得到的函数模型描述实际问题的变化规律.
建立函数模型解决问题的基本过程
1.利用函数模型求实际应用问题的最值时,要特别注意取得最值时的自变量的值与
实际意义是否相符.?( √ )
2.解决某一实际问题的函数模型是唯一的.?(????? )
提示:对于一个实际问题,可以选择不同的函数模型,只是模拟效果有区别.
3.根据收集到的数据作出散点图,结合已知的函数选择适当的函数模型,这样得到
的函数模型的模拟效果较好.( √ )
提示:根据散点图选择函数模型,针对性较强,得到的函数模型的模拟效果较好.
4.用来拟合散点图的函数图象一定要经过所有点.?(????? )
提示:拟合函数的图象不需要经过散点图中的所有点,只需误差小就行了.
判断正误,正确的画“√”
,错误的画“
?”
.
5.在建立函数模型的过程中,要求定义域只需使函数解析式有意义.?(????? )
提示:实际问题中函数的定义域不仅要使函数解析式有意义,还应使用自变量表达
的任何量都满足实际意义.
6.用函数模型预测的结果和实际结果必须相等,否则函数模型就无存在意义了.?
(????? )
提示:用函数模型预测的结果和实际结果可以有误差,好的函数模型预测的结果与
实际结果误差较小.
应用函数模型求解实际问题
?
1.已知函数模型解决实际问题时,给出的函数解析式往往含有参数,需要将题中的
数据代入函数模型,求得函数模型中的参数,再将问题转化为已知函数解析式求函
数值或自变量的值.
2.利用函数模型解决实际应用问题时,要抓住关键:选择和建立恰当的函数模型.用
得到的函数进行拟合时,可能误差较大或不切合客观实际,因此要对所得函数模型
进行检验,切忌盲目下结论.
???
物体在常温下的温度变化可以用牛顿冷却定律来描述,设物体的初始温度是
T0
℃,经过一定时间t
min后的温度是T
℃,则T-Ta=(T0-Ta)×?,其中Ta表示环境温度,
h称为半衰期.现有一杯用88
℃热水冲的速溶咖啡,放在24
℃的房间中,如果咖啡降
温到40
℃需要20
min,那么降温到32
℃,需要多长时间?
思路点拨
根据已知条件确定函数关系式,然后代值求解.
解析????由题意可得40-24=(88-24)×?,
即?=?,解得h=10,
故原式可化简为T-24=(88-24)×?,
当T=32时,代入上式,
得32-24=(88-24)×?,
即?=?=?=?,∴t=30.
因此需要30
min可降温到32
℃.
素养点评????在实际问题中,有关人口增长、银行利率、细胞分裂等增长率问题常
用指数型函数模型表示.通常可以表示为y=k(1+p)x
(k∈R,且k≠0,0为基础数,p为增长率,x为时间)的形式.
某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元,为了扩大销量,
增加盈利,尽快减少库存,商场决定采取适当降价措施.经调查发现,如果每件衬衫每
降价1元,商场平均每天可多售出2件.于是商场经理决定每件衬衫降价15元.
问题
1.请问经理的决定正确吗?
提示:判断是否正确,这需要把实际问题转化为数学问题,用函数模型来解决.
2.解决函数应用问题的基本步骤是什么?
提示:用函数知识和函数观点解决实际问题时,一般按以下几个步骤进行:①审题;
②建模;③求模;④还原.
构建函数模型解决实际问题
?建立函数模型时,求解函数解析式的方法
(1)待定系数法.已知条件中给出了含参数的函数解析式或根据已知条件可确定函
数模型,此种情形下应用待定系数法求出函数解析式中的相关参数(未知系数)的
值,进而确定函数的解析式.
(2)归纳法.先让自变量x取一些特殊值,计算出相对应的函数值,从中发现规律,再推
广到一般情形,从而得到函数的解析式.
(3)方程法.用x表示自变量或其他相关的量.根据问题的实际意义,运用已掌握的数
学、物理等方面的知识,列出函数的解析式,此种方法形式上和列方程解应用题相
仿,故称为方程法.
??
“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:“活
水围网”养鱼时,某种鱼在一定条件下,每尾鱼的平均生长速度v(单位:千克/年)是
关于养殖密度x(单位:尾/立方米)的函数.当养殖密度x不超过4尾/立方米时,v为2千
克/年;当4氧等原因,v为0千克/年.
(1)当0(2)当养殖密度x为多大时,该种鱼的年生长量f(x)(单位:千克/立方米)可以达到最大?
最大为多少?(年生长量=每尾鱼的平均生长速度×养殖密度)
思路点拨
(1)根据题意利用待定系数法求出函数解析式;(2)利用函数单调性求最值,解决实际
问题.
解析????(1)由题意得,当0当4由已知得?解得?所以v=-?x+?.故v=?
(2)依题意及(1)可得f(x)=?
当0故f(x)max=f(4)=4×2=8;
当4所以f(x)max=f(10)=?=12.5.
因为8<12.5,所以当0所以当养殖密度x为10尾/立方米时,该种鱼的年生长量f(x)可以达到最大,最大为12.
5千克/立方米.
李明家种植蔬菜,他研究了黄瓜的种植成本与上市时间的关系.黄瓜从1月1日
开始上市,通过市场调查,得到该黄瓜的种植成本Q(单位:元/10
kg)与上市时间t(单
位:10天)的数据如下表:
时间t(10天)
5
6
11
25
种植成本Q(元/10
kg)
15
14.03
10.8
15
建立拟合函数模型解决实际问题
问题
1.根据表中数据,如何选取一个合适的函数模型描述该蔬菜种植成本Q(元/10
kg)与
上市时间t(10天)的变化关系?
提示:画散点图,根据图形确定拟合函数.
2.根据散点图如何确定函数模型?
提示:根据散点分布特征对比基本函数图象确定模型类型.
3.用得到的函数进行拟合,是否一定符合实际问题?
提示:不一定.用得到的函数进行拟合时,可能误差较大或不切合客观实际,因此要
对所得函数模型进行检验,切忌盲目下结论.
?函数拟合与预测的一般步骤
(1)根据原始数据、表格,绘出散点图;
(2)通过考察散点图,画出拟合直线或拟合曲线;
(3)求出拟合直线或拟合曲线的函数关系式;
(4)利用函数关系式,根据条件对所给问题进行预测和控制,为决策和管理提供依据.
??
某商场经营一批进价为每件30元的商品,在市场销售中发现此商品的销售单
价x(元)与日销量y(件)之间有如下关系:
(1)根据表中提供的数据在平面直角坐标系中描出实数对(x,y)对应的点,并确
定x与y的一个函数关系式y=f(x);
(2)设经营此商品的日销售利润为P元,根据上述关系式写出P关于x的函数关系式,
并指出销售单价x为多少时,才能获得最大日销售利润.
思路点拨
描点?选模?求模?验模?用模
销售单价x(元)
30
40
45
50
日销售量y(件)
60
30
15
0
解析????(1)由题表中数据,在平面直角坐标系中作出实数对(30,60),(40,30),(45,15),(5
0,0)对应的点,它们近似地分布在一条直线上,如图所示.
?
设直线方程为y=kx+b(k≠0),
将点(50,0),(45,15)代入,
得?解得?
∴y=-3x+150(30≤x≤50).
经检验,(30,60),(40,30)在此直线上,
∴所求函数关系式为y=-3x+150(30≤x≤50).
(2)依题意P=y(x-30)=(-3x+150)(x-30)=-3(x-40)2+300(30≤x≤50),
∴当x=40时,P取得最大值,最大值为300.
故当销售单价为40元时,才能获得最大日销售利润.
https://www.21cnjy.com/help/help_extract.php
人教版A版(2019)
必修第一册
4.5.3 函数模型的应用
1.理解函数是描述客观世界中变量关系和规律的重要数学语言和工具.
2.在实际情境中,会选择合适的函数类型刻画现实问题的变化规律.
3.阅读、收集一些现实生活、实际生产或者经济领域中的数学模型,体会人们是如
何借助函数刻画实际问题的,感悟数学模型中参数的现实意义.
?
一次函数模型
y=kx+b(k,b为常数,k≠0)
二次函数模型
y=ax2+bx+c(a,b,c为常数,a≠0)
指数型函数模型
y=bax+c(a,b,c为常数,b≠0,a>0
且a≠1)
对数型函数模型
y=mlogax+n(m,a,n为常数,m≠
0,a>0且a≠1)
幂函数型模型
y=axn+b(a,n,b为常数,a≠0)
常见的函数模型
1.用函数模型解决实际问题的基本过程
2.建立函数模型解决实际问题的步骤
(1)审题——弄清题意,分清条件和要求的结论,理顺数量关系,初步选择函数模型;
(2)建模——将自然语言转化为数学语言,将文字语言转化为符号语言,利用数学知
识建立相应的函数模型;
(3)求模——推理并求解函数模型;
(4)还原——用得到的函数模型描述实际问题的变化规律.
建立函数模型解决问题的基本过程
1.利用函数模型求实际应用问题的最值时,要特别注意取得最值时的自变量的值与
实际意义是否相符.?( √ )
2.解决某一实际问题的函数模型是唯一的.?(????? )
提示:对于一个实际问题,可以选择不同的函数模型,只是模拟效果有区别.
3.根据收集到的数据作出散点图,结合已知的函数选择适当的函数模型,这样得到
的函数模型的模拟效果较好.( √ )
提示:根据散点图选择函数模型,针对性较强,得到的函数模型的模拟效果较好.
4.用来拟合散点图的函数图象一定要经过所有点.?(????? )
提示:拟合函数的图象不需要经过散点图中的所有点,只需误差小就行了.
判断正误,正确的画“√”
,错误的画“
?”
.
5.在建立函数模型的过程中,要求定义域只需使函数解析式有意义.?(????? )
提示:实际问题中函数的定义域不仅要使函数解析式有意义,还应使用自变量表达
的任何量都满足实际意义.
6.用函数模型预测的结果和实际结果必须相等,否则函数模型就无存在意义了.?
(????? )
提示:用函数模型预测的结果和实际结果可以有误差,好的函数模型预测的结果与
实际结果误差较小.
应用函数模型求解实际问题
?
1.已知函数模型解决实际问题时,给出的函数解析式往往含有参数,需要将题中的
数据代入函数模型,求得函数模型中的参数,再将问题转化为已知函数解析式求函
数值或自变量的值.
2.利用函数模型解决实际应用问题时,要抓住关键:选择和建立恰当的函数模型.用
得到的函数进行拟合时,可能误差较大或不切合客观实际,因此要对所得函数模型
进行检验,切忌盲目下结论.
???
物体在常温下的温度变化可以用牛顿冷却定律来描述,设物体的初始温度是
T0
℃,经过一定时间t
min后的温度是T
℃,则T-Ta=(T0-Ta)×?,其中Ta表示环境温度,
h称为半衰期.现有一杯用88
℃热水冲的速溶咖啡,放在24
℃的房间中,如果咖啡降
温到40
℃需要20
min,那么降温到32
℃,需要多长时间?
思路点拨
根据已知条件确定函数关系式,然后代值求解.
解析????由题意可得40-24=(88-24)×?,
即?=?,解得h=10,
故原式可化简为T-24=(88-24)×?,
当T=32时,代入上式,
得32-24=(88-24)×?,
即?=?=?=?,∴t=30.
因此需要30
min可降温到32
℃.
素养点评????在实际问题中,有关人口增长、银行利率、细胞分裂等增长率问题常
用指数型函数模型表示.通常可以表示为y=k(1+p)x
(k∈R,且k≠0,0
某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元,为了扩大销量,
增加盈利,尽快减少库存,商场决定采取适当降价措施.经调查发现,如果每件衬衫每
降价1元,商场平均每天可多售出2件.于是商场经理决定每件衬衫降价15元.
问题
1.请问经理的决定正确吗?
提示:判断是否正确,这需要把实际问题转化为数学问题,用函数模型来解决.
2.解决函数应用问题的基本步骤是什么?
提示:用函数知识和函数观点解决实际问题时,一般按以下几个步骤进行:①审题;
②建模;③求模;④还原.
构建函数模型解决实际问题
?建立函数模型时,求解函数解析式的方法
(1)待定系数法.已知条件中给出了含参数的函数解析式或根据已知条件可确定函
数模型,此种情形下应用待定系数法求出函数解析式中的相关参数(未知系数)的
值,进而确定函数的解析式.
(2)归纳法.先让自变量x取一些特殊值,计算出相对应的函数值,从中发现规律,再推
广到一般情形,从而得到函数的解析式.
(3)方程法.用x表示自变量或其他相关的量.根据问题的实际意义,运用已掌握的数
学、物理等方面的知识,列出函数的解析式,此种方法形式上和列方程解应用题相
仿,故称为方程法.
??
“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:“活
水围网”养鱼时,某种鱼在一定条件下,每尾鱼的平均生长速度v(单位:千克/年)是
关于养殖密度x(单位:尾/立方米)的函数.当养殖密度x不超过4尾/立方米时,v为2千
克/年;当4
(1)当0
最大为多少?(年生长量=每尾鱼的平均生长速度×养殖密度)
思路点拨
(1)根据题意利用待定系数法求出函数解析式;(2)利用函数单调性求最值,解决实际
问题.
解析????(1)由题意得,当0
(2)依题意及(1)可得f(x)=?
当0
当4
因为8<12.5,所以当0
5千克/立方米.
李明家种植蔬菜,他研究了黄瓜的种植成本与上市时间的关系.黄瓜从1月1日
开始上市,通过市场调查,得到该黄瓜的种植成本Q(单位:元/10
kg)与上市时间t(单
位:10天)的数据如下表:
时间t(10天)
5
6
11
25
种植成本Q(元/10
kg)
15
14.03
10.8
15
建立拟合函数模型解决实际问题
问题
1.根据表中数据,如何选取一个合适的函数模型描述该蔬菜种植成本Q(元/10
kg)与
上市时间t(10天)的变化关系?
提示:画散点图,根据图形确定拟合函数.
2.根据散点图如何确定函数模型?
提示:根据散点分布特征对比基本函数图象确定模型类型.
3.用得到的函数进行拟合,是否一定符合实际问题?
提示:不一定.用得到的函数进行拟合时,可能误差较大或不切合客观实际,因此要
对所得函数模型进行检验,切忌盲目下结论.
?函数拟合与预测的一般步骤
(1)根据原始数据、表格,绘出散点图;
(2)通过考察散点图,画出拟合直线或拟合曲线;
(3)求出拟合直线或拟合曲线的函数关系式;
(4)利用函数关系式,根据条件对所给问题进行预测和控制,为决策和管理提供依据.
??
某商场经营一批进价为每件30元的商品,在市场销售中发现此商品的销售单
价x(元)与日销量y(件)之间有如下关系:
(1)根据表中提供的数据在平面直角坐标系中描出实数对(x,y)对应的点,并确
定x与y的一个函数关系式y=f(x);
(2)设经营此商品的日销售利润为P元,根据上述关系式写出P关于x的函数关系式,
并指出销售单价x为多少时,才能获得最大日销售利润.
思路点拨
描点?选模?求模?验模?用模
销售单价x(元)
30
40
45
50
日销售量y(件)
60
30
15
0
解析????(1)由题表中数据,在平面直角坐标系中作出实数对(30,60),(40,30),(45,15),(5
0,0)对应的点,它们近似地分布在一条直线上,如图所示.
?
设直线方程为y=kx+b(k≠0),
将点(50,0),(45,15)代入,
得?解得?
∴y=-3x+150(30≤x≤50).
经检验,(30,60),(40,30)在此直线上,
∴所求函数关系式为y=-3x+150(30≤x≤50).
(2)依题意P=y(x-30)=(-3x+150)(x-30)=-3(x-40)2+300(30≤x≤50),
∴当x=40时,P取得最大值,最大值为300.
故当销售单价为40元时,才能获得最大日销售利润.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
