3.2.1 单调性与最大(小)值 课件(共29张PPT)
文档属性
| 名称 | 3.2.1 单调性与最大(小)值 课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-28 16:05:51 | ||
图片预览








文档简介
(共29张PPT)
人教版A版(2019)
必修第一册
3.2
函数的基本性质
3.2.1 单调性与最大(小)值
1.借助函数图象,会用符号语言表达函数的单调性、函数的最大值、函数的最小
值.
2.理解单调区间、单调性等概念,会用定义证明函数的单调性.
3.理解函数单调性的作用与实际意义,会求函数的单调区间,并判断单调性.
4.理解函数的最大(小)值的作用和实际意义,会借助单调性求函数的最大(小)值.
增函数
减函数
条件
一般地,设函数f(x)的定义域为I,区间①????D?I????
如果②?????x1,x2∈D????,当x1③????f(x1)⑤????f(x1)>f(x2)????
结论
那么就称函数f(x)在区间D上④ 单调递增????
那么就称函数f(x)在区间D上⑥ 单调递减????
图示
?
?
图象
特征
函数f(x)在区间D上的图象是上升的
函数f(x)在区间D上的图象是下降的
增函数与减函数的定义
特别地,当函数y=f(x)在它的定义域上⑦ 单调递增????或⑧ 单调递减????时,我
们就称它是⑨ 增函数????或⑩ 减函数????.
如果函数f(x)在区间D上单调递增或单调递减,那么就说函数y=f(x)在这一区间
具有(严格的)? 单调性????,区间D叫做y=f(x)的? 单调区间????.
最大值
最小值
条件
一般地,设函数y=f(x)的定义域为I,如果存在实数M满足:?x∈I,都
有
?????f(x)≤M????
?????f(x)≥M????
?x0∈I,使得?????f(x0)=M????
结论
那么,称M是函数y=f(x)的最大值
那么,称M是函数y=f(x)的最小值
几何
意义
f(x)图象上最高点的? 纵坐标
????
f(x)图象上最低点的? 纵坐标
????
函数的最大值与最小值
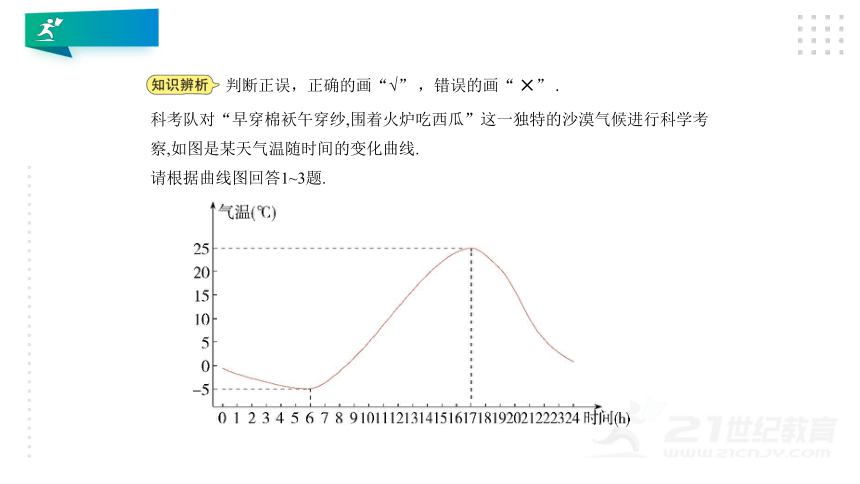
科考队对“早穿棉袄午穿纱,围着火炉吃西瓜”这一独特的沙漠气候进行科学考
察,如图是某天气温随时间的变化曲线.
请根据曲线图回答1~3题.
?
判断正误,正确的画“√”
,错误的画“
?”
.
1.该天的最高气温为25
℃,最低气温为-5
℃.?( √ )
2.该天气温在6时至17时内随着时间增加而增加.( √ )
3.该天的温差是20
℃.?(????? )
4.函数f(x)取最大值时,对应的x可能有无限多个.( √ )
提示:例如:f(x)=?f(x)的最大值为1,
f(x)取最大值时,x的值的集合为(0,+∞),有
无数个值.
5.若函数f(x)在区间(1,2]和(2,3)上均为增函数,则函数f(x)在区间(1,3)上为增函数.
(????? )
提示:例如:f(x)=?f(x)在区间(1,2]和(2,3)上均为增函数,但由图象(图略)知
函数f(x)在区间(1,3)上不是增函数.
6.若函数f(x)在区间[a,b]上是增函数,则f(x)在区间[a,b]上的最小值是f(a),最大值是f
(b).( √ )
提示:由于函数f(x)在区间[a,b]上是增函数,所以f(a)≤f(x)≤f(b).故f(x)的最小值是f
(a),最大值是f(b).
如何判断或证明函数的单调性
?判断或证明函数单调性的常用方法
1.定义法.根据增函数、减函数的定义,按照“取值→作差→变形→判断符号→下
结论”进行判断.
单调性判断的等价结论:
当x∈D时,f(x)是增函数,?x1,x2∈D且x1≠x2,则(x1-x2)[f(x1)-f(x2)]>0??>0.
当x∈D时,f(x)是减函数,?x1,x2∈D且x1≠x2,则(x1-x2)[f(x1)-f(x2)]<0??<0.
2.图象法.根据函数图象的升降情况进行判断.
3.直接法.运用已知结论,直接得到函数的单调性,如一次函数、二次函数、反比例
函数的单调性均可直接得出.
4.复合函数单调性的判断依据如下:
(1)若u=g(x),y=f(u)在所讨论的区间上都是增函数或都是减函数,则y=f(g(x))为增函
数;
(2)若u=g(x),y=f(u)在所讨论的区间上一个是增函数,另一个是减函数,则y=f(g(x))为
减函数.
列表如下:
复合函数的单调性可简记为“同增异减”,即内外函数的单调性相同时单调
递增;相异时单调递减.
u=g(x)
y=f(u)
y=f(g(x))
增
增
增
增
减
减
减
增
减
减
减
增
利用定义证明下列函数的单调性:
(1)f(x)=x3在R上是增函数;
(2)f(x)=?在[0,+∞)上是增函数.
证明????(1)任取R上的两个实数x1,x2,且x1则f(x1)-f(x2)=?-?=(x1-x2)(?+x1x2+?)=(x1-x2)?,
∵x1又?≥0,??≥0,且两个等号不能同时成立,
∴?+??>0,∴f(x1)-f(x2)<0,
即f(x1)(2)任取[0,+∞)上的两个实数x1,x2,且x1则f(x1)-f(x2)=?-?
=?=?.
∵0≤x10,
∴f(x1)-f(x2)<0,即f(x1)∴f(x)=?在[0,+∞)上是增函数.
??
设函数f(x)的定义域是(0,+∞),且对任意正实数x,y,f(xy)=f(x)+f(y)恒成立,已知f
(2)=1,且当x>1时,
f(x)>0.
(1)求f?的值;
(2)判断y=f(x)在(0,+∞)上的单调性并给出证明.
思路点拨
抽象函数问题解题的关键是根据结论对x,y进行赋值,通过赋值解决.
解析????(1)∵对于任意正实数x,y,
f(xy)=f(x)+f(y)恒成立,
∴当x=y=1时,有f(1)=f(1)+f(1),∴f(1)=0.
当x=2,y=?时,有f?=f(2)+f?,即f(2)+f?=0,又f(2)=1,∴f?=-1.
(2)y=f(x)在(0,+∞)上为增函数.证明如下:
任取x1,x2∈(0,+∞),且x1则f(x1)+f
?=f(x2),
即f(x2)-f(x1)=f
?.
∵?>1,∴f
?>0,
即f(x2)>f(x1),
∴f(x)在(0,+∞)上为增函数.
利用函数的单调性解不等式
1.利用函数的单调性解不等式主要依据函数单调性的定义和性质,将符号“f”脱
掉,列出关于未知量的不等式(组),然后求解,此时注意函数的定义域.
2.解有关抽象函数的不等式问题的一般步骤:
(1)将不等式化为f(x1)(2)若函数f(x)是D上的增函数,则x1,x2∈D,且x1∈D,且x1>x2.
根据函数的单调性确定参数的取值范围
1.利用单调性的定义:在单调区间内任取x1,x2,且x10)
恒成立求参数的取值范围.
2.利用具体函数本身所具有的特征:如二次函数的图象被对称轴一分为二,可根据
对称轴相对于所给单调区间的位置建立关于参数的不等式(组),解不等式(组),求出
如何利用函数的单调性解决相关函数问题
参数的取值范围.
注意:若某个函数在区间[a,b]上是单调的,则该函数在此区间的任意子集上也是单
调的.
对于分段函数由单调性求参问题,一般从两方面考虑:一方面每个分段区间上函数
具有相同的单调性,由此列出相关式子;
另一方面要考虑分界点处函数值之间的大
小关系,由此列出另外的式子,从而解得参数的取值范围.
??
已知函数y=f(x)在定义域(-1,1)上是减函数,且f(2a-1)围是?(????B )
A.? ????B.?
C.(0,2) ????D.(0,+∞)
思路点拨
利用单调性结合定义域去掉“f”,进而求解不等式组.
解析????函数y=f(x)在定义域(-1,1)上是减函数,
则有?
解得?故实数a的取值范围是?.故选B.
??
若函数f(x)=?是(-∞,+∞)上的减函数,则实数a的取值范围是?(????B
)
A.(-2,0) ????B.[-2,0)
C.(-∞,1] ????D.(-∞,0)
思路点拨
结合分段函数的单调性,讨论每段函数满足减函数时的条件以及两段函数分界点
处函数值的关系,列出不等式组求解.
解析????因为f(x)=?是定义在(-∞,+∞)上的减函数,
所以?
解得-2≤a<0.故实数a的取值范围是[-2,0).
??
(1)已知f(x)=x2-2(1-a)x+2在(-∞,4]上是减函数,求实数a的取值范围;
(2)已知f(x)=-x3+ax在(0,1)上是增函数,求实数a的取值范围.
解析????(1)要使f(x)在(-∞,4]上是减函数,
需满足x=-?≥4,
解得a≤-3.
∴实数a的取值范围是(-∞,-3].
(2)任取x1,x2∈(0,1),
且x1则f(x1)-f(x2)=(-?+ax1)-(-?+ax2)=(?-?)+a(x1-x2)=(x2-x1)(?+x1x2+?-a).
∵f(x)在(0,1)上是增函数,
∴f(x1)-f(x2)<0.
∵00,?+x1x2+?<3,
∴?+x1x2+?-a<0,
∴a>?+x1x2+?,
∴a≥3.
∴实数a的取值范围是[3,+∞).
求二次函数在某闭区间上最大(小)值问题的解法
1.含参数的二次函数最大(小)值问题的解法:
解决含参数的二次函数的最值问题,首先将二次函数化为y=a(x-h)2+k的形式,再由a
的符号确定抛物线的开口方向,根据对称轴x=h得出顶点的位置,再根据x的定义区
间结合大致图象确定最大或最小值.
2.对于含参数的二次函数的最值问题,一般有下列几种类型:
(1)区间固定,对称轴变动(含参数),求最值;
(2)对称轴固定,区间变动(含参数),求最值;
(3)区间固定,最值也固定,对称轴变动,求参数.
求解时通常都是根据区间端点和对称轴的相对位置进行分类讨论.
如何求二次函数在某闭区间上的最大(小)值
??
求函数f(x)=x2-2ax-1在区间[0,2]上的最大值和最小值.
思路点拨
由于二次函数的最值与其图象的对称轴位置有关,而题中函数图象的对称轴为直
线x=a,其位置不确定,所以应按函数图象的对称轴与x轴的交点的横坐标和区间[0,
2]的相对位置进行分类讨论.
解析????f(x)=(x-a)2-1-a2,其图象的对称轴为直线x=a.
(1)当a<0时,由图①可知,
f(x)min=f(0)=-1,
f(x)max=f(2)=3-4a.
?
(2)当0≤a≤1时,由图②可知,
f(x)min=f(a)=-1-a2,
f(x)max=f(2)=3-4a.
(3)当1f(x)min=f(a)=-1-a2,
f(x)max=f(0)=-1.
(4)当a>2时,由图④可知,
f(x)min=f(2)=3-4a,
f(x)max=f(0)=-1.
导师点睛????本题不是分a<0,0≤a≤2,a>2三种情况讨论,而是分四种情况,这是由于
抛物线的对称轴在区间[0,2]内时,最小值是在顶点处取得的,但最大值有可能是f
(0),也有可能是f(2).本题考查了直观想象及逻辑推理的核心素养.
??
求函数f(x)=x2-2x+2在区间[t,t+1]上的最小值g(t).
思路点拨
因为图象的对称轴固定,区间不定,所以可以从三个方面进行讨论:①图象的对称轴
在区间左侧;②图象的对称轴在区间右侧;③图象的对称轴在区间内.
解析????f(x)=x2-2x+2=(x-1)2+1,x∈[t,t+1],t∈R,其图象的对称轴为直线x=1.
?
当t+1<1,即t<0时,函数图象如图①所示,
f(x)在区间[t,t+1]上为减函数,所以g(t)=
f(t+1)=t2+1;当t≤1≤t+1,即0≤t≤1时,函数图象如图②所示,g(t)=f(1)=1;当t>1时,函
数图象如图③所示,
f(x)在区间[t,t+1]上为增函数,所以g(t)=f(t)=t2-2t+2.
综上,可得g(t)=?
??
已知函数f(x)=x2-2x+3在闭区间[0,m]上有最大值3,最小值2,求m的取值范围.
解析????作出函数
f(x)
=x2-2x+3=(x-1)2+2的图象如图所示,由图可知f(1)=2,f(0)=f(2)=
3,
因为f(x)min=2,
f(x)max=3,
所以结合图象可得1≤m≤2.
?
https://www.21cnjy.com/help/help_extract.php
人教版A版(2019)
必修第一册
3.2
函数的基本性质
3.2.1 单调性与最大(小)值
1.借助函数图象,会用符号语言表达函数的单调性、函数的最大值、函数的最小
值.
2.理解单调区间、单调性等概念,会用定义证明函数的单调性.
3.理解函数单调性的作用与实际意义,会求函数的单调区间,并判断单调性.
4.理解函数的最大(小)值的作用和实际意义,会借助单调性求函数的最大(小)值.
增函数
减函数
条件
一般地,设函数f(x)的定义域为I,区间①????D?I????
如果②?????x1,x2∈D????,当x1
结论
那么就称函数f(x)在区间D上④ 单调递增????
那么就称函数f(x)在区间D上⑥ 单调递减????
图示
?
?
图象
特征
函数f(x)在区间D上的图象是上升的
函数f(x)在区间D上的图象是下降的
增函数与减函数的定义
特别地,当函数y=f(x)在它的定义域上⑦ 单调递增????或⑧ 单调递减????时,我
们就称它是⑨ 增函数????或⑩ 减函数????.
如果函数f(x)在区间D上单调递增或单调递减,那么就说函数y=f(x)在这一区间
具有(严格的)? 单调性????,区间D叫做y=f(x)的? 单调区间????.
最大值
最小值
条件
一般地,设函数y=f(x)的定义域为I,如果存在实数M满足:?x∈I,都
有
?????f(x)≤M????
?????f(x)≥M????
?x0∈I,使得?????f(x0)=M????
结论
那么,称M是函数y=f(x)的最大值
那么,称M是函数y=f(x)的最小值
几何
意义
f(x)图象上最高点的? 纵坐标
????
f(x)图象上最低点的? 纵坐标
????
函数的最大值与最小值
科考队对“早穿棉袄午穿纱,围着火炉吃西瓜”这一独特的沙漠气候进行科学考
察,如图是某天气温随时间的变化曲线.
请根据曲线图回答1~3题.
?
判断正误,正确的画“√”
,错误的画“
?”
.
1.该天的最高气温为25
℃,最低气温为-5
℃.?( √ )
2.该天气温在6时至17时内随着时间增加而增加.( √ )
3.该天的温差是20
℃.?(????? )
4.函数f(x)取最大值时,对应的x可能有无限多个.( √ )
提示:例如:f(x)=?f(x)的最大值为1,
f(x)取最大值时,x的值的集合为(0,+∞),有
无数个值.
5.若函数f(x)在区间(1,2]和(2,3)上均为增函数,则函数f(x)在区间(1,3)上为增函数.
(????? )
提示:例如:f(x)=?f(x)在区间(1,2]和(2,3)上均为增函数,但由图象(图略)知
函数f(x)在区间(1,3)上不是增函数.
6.若函数f(x)在区间[a,b]上是增函数,则f(x)在区间[a,b]上的最小值是f(a),最大值是f
(b).( √ )
提示:由于函数f(x)在区间[a,b]上是增函数,所以f(a)≤f(x)≤f(b).故f(x)的最小值是f
(a),最大值是f(b).
如何判断或证明函数的单调性
?判断或证明函数单调性的常用方法
1.定义法.根据增函数、减函数的定义,按照“取值→作差→变形→判断符号→下
结论”进行判断.
单调性判断的等价结论:
当x∈D时,f(x)是增函数,?x1,x2∈D且x1≠x2,则(x1-x2)[f(x1)-f(x2)]>0??>0.
当x∈D时,f(x)是减函数,?x1,x2∈D且x1≠x2,则(x1-x2)[f(x1)-f(x2)]<0??<0.
2.图象法.根据函数图象的升降情况进行判断.
3.直接法.运用已知结论,直接得到函数的单调性,如一次函数、二次函数、反比例
函数的单调性均可直接得出.
4.复合函数单调性的判断依据如下:
(1)若u=g(x),y=f(u)在所讨论的区间上都是增函数或都是减函数,则y=f(g(x))为增函
数;
(2)若u=g(x),y=f(u)在所讨论的区间上一个是增函数,另一个是减函数,则y=f(g(x))为
减函数.
列表如下:
复合函数的单调性可简记为“同增异减”,即内外函数的单调性相同时单调
递增;相异时单调递减.
u=g(x)
y=f(u)
y=f(g(x))
增
增
增
增
减
减
减
增
减
减
减
增
利用定义证明下列函数的单调性:
(1)f(x)=x3在R上是增函数;
(2)f(x)=?在[0,+∞)上是增函数.
证明????(1)任取R上的两个实数x1,x2,且x1
∵x1
∴?+??>0,∴f(x1)-f(x2)<0,
即f(x1)
=?=?.
∵0≤x1
∴f(x1)-f(x2)<0,即f(x1)
??
设函数f(x)的定义域是(0,+∞),且对任意正实数x,y,f(xy)=f(x)+f(y)恒成立,已知f
(2)=1,且当x>1时,
f(x)>0.
(1)求f?的值;
(2)判断y=f(x)在(0,+∞)上的单调性并给出证明.
思路点拨
抽象函数问题解题的关键是根据结论对x,y进行赋值,通过赋值解决.
解析????(1)∵对于任意正实数x,y,
f(xy)=f(x)+f(y)恒成立,
∴当x=y=1时,有f(1)=f(1)+f(1),∴f(1)=0.
当x=2,y=?时,有f?=f(2)+f?,即f(2)+f?=0,又f(2)=1,∴f?=-1.
(2)y=f(x)在(0,+∞)上为增函数.证明如下:
任取x1,x2∈(0,+∞),且x1
?=f(x2),
即f(x2)-f(x1)=f
?.
∵?>1,∴f
?>0,
即f(x2)>f(x1),
∴f(x)在(0,+∞)上为增函数.
利用函数的单调性解不等式
1.利用函数的单调性解不等式主要依据函数单调性的定义和性质,将符号“f”脱
掉,列出关于未知量的不等式(组),然后求解,此时注意函数的定义域.
2.解有关抽象函数的不等式问题的一般步骤:
(1)将不等式化为f(x1)
根据函数的单调性确定参数的取值范围
1.利用单调性的定义:在单调区间内任取x1,x2,且x1
恒成立求参数的取值范围.
2.利用具体函数本身所具有的特征:如二次函数的图象被对称轴一分为二,可根据
对称轴相对于所给单调区间的位置建立关于参数的不等式(组),解不等式(组),求出
如何利用函数的单调性解决相关函数问题
参数的取值范围.
注意:若某个函数在区间[a,b]上是单调的,则该函数在此区间的任意子集上也是单
调的.
对于分段函数由单调性求参问题,一般从两方面考虑:一方面每个分段区间上函数
具有相同的单调性,由此列出相关式子;
另一方面要考虑分界点处函数值之间的大
小关系,由此列出另外的式子,从而解得参数的取值范围.
??
已知函数y=f(x)在定义域(-1,1)上是减函数,且f(2a-1)
A.? ????B.?
C.(0,2) ????D.(0,+∞)
思路点拨
利用单调性结合定义域去掉“f”,进而求解不等式组.
解析????函数y=f(x)在定义域(-1,1)上是减函数,
则有?
解得?
??
若函数f(x)=?是(-∞,+∞)上的减函数,则实数a的取值范围是?(????B
)
A.(-2,0) ????B.[-2,0)
C.(-∞,1] ????D.(-∞,0)
思路点拨
结合分段函数的单调性,讨论每段函数满足减函数时的条件以及两段函数分界点
处函数值的关系,列出不等式组求解.
解析????因为f(x)=?是定义在(-∞,+∞)上的减函数,
所以?
解得-2≤a<0.故实数a的取值范围是[-2,0).
??
(1)已知f(x)=x2-2(1-a)x+2在(-∞,4]上是减函数,求实数a的取值范围;
(2)已知f(x)=-x3+ax在(0,1)上是增函数,求实数a的取值范围.
解析????(1)要使f(x)在(-∞,4]上是减函数,
需满足x=-?≥4,
解得a≤-3.
∴实数a的取值范围是(-∞,-3].
(2)任取x1,x2∈(0,1),
且x1
∵f(x)在(0,1)上是增函数,
∴f(x1)-f(x2)<0.
∵0
∴?+x1x2+?-a<0,
∴a>?+x1x2+?,
∴a≥3.
∴实数a的取值范围是[3,+∞).
求二次函数在某闭区间上最大(小)值问题的解法
1.含参数的二次函数最大(小)值问题的解法:
解决含参数的二次函数的最值问题,首先将二次函数化为y=a(x-h)2+k的形式,再由a
的符号确定抛物线的开口方向,根据对称轴x=h得出顶点的位置,再根据x的定义区
间结合大致图象确定最大或最小值.
2.对于含参数的二次函数的最值问题,一般有下列几种类型:
(1)区间固定,对称轴变动(含参数),求最值;
(2)对称轴固定,区间变动(含参数),求最值;
(3)区间固定,最值也固定,对称轴变动,求参数.
求解时通常都是根据区间端点和对称轴的相对位置进行分类讨论.
如何求二次函数在某闭区间上的最大(小)值
??
求函数f(x)=x2-2ax-1在区间[0,2]上的最大值和最小值.
思路点拨
由于二次函数的最值与其图象的对称轴位置有关,而题中函数图象的对称轴为直
线x=a,其位置不确定,所以应按函数图象的对称轴与x轴的交点的横坐标和区间[0,
2]的相对位置进行分类讨论.
解析????f(x)=(x-a)2-1-a2,其图象的对称轴为直线x=a.
(1)当a<0时,由图①可知,
f(x)min=f(0)=-1,
f(x)max=f(2)=3-4a.
?
(2)当0≤a≤1时,由图②可知,
f(x)min=f(a)=-1-a2,
f(x)max=f(2)=3-4a.
(3)当1
f(x)max=f(0)=-1.
(4)当a>2时,由图④可知,
f(x)min=f(2)=3-4a,
f(x)max=f(0)=-1.
导师点睛????本题不是分a<0,0≤a≤2,a>2三种情况讨论,而是分四种情况,这是由于
抛物线的对称轴在区间[0,2]内时,最小值是在顶点处取得的,但最大值有可能是f
(0),也有可能是f(2).本题考查了直观想象及逻辑推理的核心素养.
??
求函数f(x)=x2-2x+2在区间[t,t+1]上的最小值g(t).
思路点拨
因为图象的对称轴固定,区间不定,所以可以从三个方面进行讨论:①图象的对称轴
在区间左侧;②图象的对称轴在区间右侧;③图象的对称轴在区间内.
解析????f(x)=x2-2x+2=(x-1)2+1,x∈[t,t+1],t∈R,其图象的对称轴为直线x=1.
?
当t+1<1,即t<0时,函数图象如图①所示,
f(x)在区间[t,t+1]上为减函数,所以g(t)=
f(t+1)=t2+1;当t≤1≤t+1,即0≤t≤1时,函数图象如图②所示,g(t)=f(1)=1;当t>1时,函
数图象如图③所示,
f(x)在区间[t,t+1]上为增函数,所以g(t)=f(t)=t2-2t+2.
综上,可得g(t)=?
??
已知函数f(x)=x2-2x+3在闭区间[0,m]上有最大值3,最小值2,求m的取值范围.
解析????作出函数
f(x)
=x2-2x+3=(x-1)2+2的图象如图所示,由图可知f(1)=2,f(0)=f(2)=
3,
因为f(x)min=2,
f(x)max=3,
所以结合图象可得1≤m≤2.
?
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
