3.3 幂函数 课件(共15张PPT)
文档属性
| 名称 | 3.3 幂函数 课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-28 16:07:52 | ||
图片预览






文档简介
(共15张PPT)
人教版A版(2019)
必修第一册
3.3
幂函数
学习本节内容要从概念、图象及性质理解幂函数.学习时还应掌握以下几点:
1.了解幂函数的概念,会求幂函数的解析式.
2.通过具体实例,结合y=x,y=x-1,y=x2,y=?,y=x3的图象,理解它们的变化规律.
3.能利用幂函数的单调性比较大小.
一般地,函数①????y=xα????叫做幂函数,其中x是自变量,α是常数.
幂函数的概念
幂函数
y=x
y=x2
y=x3
y=?
y=x-1
图象
?
?
?
?
?
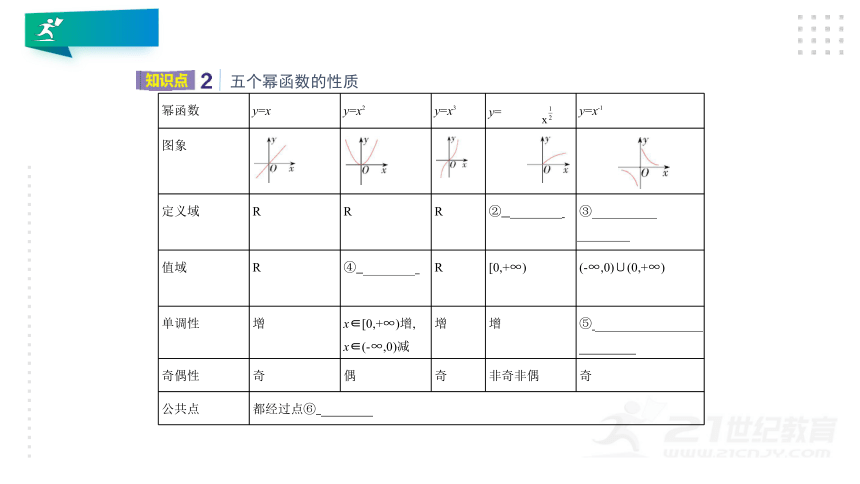
定义域
R
R
R
② [0,+∞)????
③ (-∞,0)∪
(0,+∞)????
值域
R
④ [0,+∞)????
R
[0,+∞)
(-∞,0)∪(0,+∞)
单调性
增
x∈[0,+∞)增,
x∈(-∞,0)减
增
增
⑤????x∈(0,+∞)减,x∈(-∞,0)减????
奇偶性
奇
偶
奇
非奇非偶
奇
公共点
都经过点⑥ (1,1)????
五个幂函数的性质
1.幂函数的图象都过点(0,0),(1,1).?(????? )
2.幂函数的图象一定不能出现在第四象限,但可能出现在第二象限.?( √ )
3.当幂指数α取1,3,?时,幂函数y=xα是增函数.( √ )
4.当幂指数α=-1时,幂函数y=xα在定义域上是减函数.?(????? )
5.当α=0时,幂函数y=xα的图象是一条直线.?(????? )
6.若幂函数y=xα的图象关于原点对称,则y=xα在定义域内y随x的增大而增大.?(?????
)
判断正误,正确的画“√”
,错误的画“
?”
.
如何把握幂函数的图象
解决幂函数图象问题应把握的两个原则
(1)根据幂函数在第一象限内的图象确定幂指数α(α>0)的大小关系.依据图象高低
判断幂指数的大小,相关结论如下:
①在x∈(0,1)上,指数越大,幂函数的图象越靠近x轴(简记为指大图低);
②在x∈(1,+∞)上,指数越大,幂函数的图象越远离x轴(简记为指大图高).
(2)利用定义域及奇偶性确定函数在其他象限的图象.
??
若点(?,2)在幂函数f(x)(x≠0)的图象上,点?在幂函数g(x)的图象上,问:当
x为何值时,
(1)f(x)>g(x)?(2)f(x)=g(x)?(3)f(x)思路点拨
先由点在图象上确定幂函数的解析式,再由解析式得到大致图象,利用图象解决问
题.
解析????设f(x)=xα,因为点(?,2)在幂函数f(x)的图象上,所以将点(?,2)代入f(x)=xα中,
得2=(?)α,解得α=2,则f(x)=x2.同理,可求得g(x)=x-2.
在同一平面直角坐标系中作出幂函数f(x)=x2和g(x)=x-2的图象(如图所示).
?
观察图象可得:
(1)当x>1或x<-1时,
f(x)>g(x).
(2)当x=1或x=-1时,
f(x)=g(x).
(3)当-1f(x) 已知幂函数f(x)=?,其中m∈{m|-2上的增函数;(2)?x∈R,都有f(-x)+f(x)=0.
问题
1.是否存在同时满足(1)(2)的幂函数f(x)?
提示:因为m∈{m|-2由f(x)是(0,+∞)上的增函数,得-2m2-m+3>0,解得-?又?x∈R,都有f(-x)+f(x)=0,即f(-x)=-f(x),所以f(x)是奇函数,即-2m2-m+3是奇数.③
由①②③得m=0.因此存在同时满足(1)(2)的幂函数f(x).
2.若存在,如何求出f(x)的解析式,以及x∈[0,3]时f(x)的值域?
提示:由问题1知m=0,此时f(x)=x3,且在区间[0,3]上是增函数,所以当x∈[0,3]时,函数f
(x)的值域为[0,27].
如何运用幂函数的性质解决相关问题
?
幂函数的性质与参数α可以互相确定:
(1)幂函数y=xα中只有一个参数α,幂函数的所有性质都与α的取值有关,故可由α确定
幂函数的定义域、值域、单调性、奇偶性.
(2)反过来,也可由幂函数的性质去限制α的取值:
①利用幂函数的单调性求出α的取值范围;
②由奇偶性结合所给条件确定α的值.
??
已知幂函数y=x3m-9(m∈N
)的图象关于y轴对称,且y=x3m-9(m∈N
)在(0,+∞)上单
调递减,求满足?思路点拨
由幂函数的性质确定参数m的值,再由函数的单调性解不等式.
解析????因为函数y=x3m-9(m∈N
)在(0,+∞)上单调递减,所以3m-9<0,解得m<3.
又m∈N
,所以m=1或m=2.
因为幂函数y=x3m-9的图象关于y轴对称,所以3m-9为偶数,故m=1,则原不等式可化为
(a+1?<(3-2a?.
易知y=?在(-∞,0)和(0,+∞)上单调递减,且当x<0时,y<0,当x>0时,y>0,
所以a+1>3-2a>0或3-2a解得?故a的取值范围是?a?a<-1或??
??
比较下列各组数的大小.
(1)1.?,1.?;(2)(-1.2?,(-1.25?.
思路点拨
构造幂函数,利用幂函数的性质比较各组数的大小.
解析????(1)∵函数y=?在第一象限内单调递增,且1.5<1.7,∴1.?<1.?.
(2)∵(-1.2?=1.?,(-1.25?=1.2?,
且函数y=?在第一象限内单调递减,1.2<1.25,
∴1.?>1.2?,即(-1.2?>(-1.25?.
https://www.21cnjy.com/help/help_extract.php
人教版A版(2019)
必修第一册
3.3
幂函数
学习本节内容要从概念、图象及性质理解幂函数.学习时还应掌握以下几点:
1.了解幂函数的概念,会求幂函数的解析式.
2.通过具体实例,结合y=x,y=x-1,y=x2,y=?,y=x3的图象,理解它们的变化规律.
3.能利用幂函数的单调性比较大小.
一般地,函数①????y=xα????叫做幂函数,其中x是自变量,α是常数.
幂函数的概念
幂函数
y=x
y=x2
y=x3
y=?
y=x-1
图象
?
?
?
?
?
定义域
R
R
R
② [0,+∞)????
③ (-∞,0)∪
(0,+∞)????
值域
R
④ [0,+∞)????
R
[0,+∞)
(-∞,0)∪(0,+∞)
单调性
增
x∈[0,+∞)增,
x∈(-∞,0)减
增
增
⑤????x∈(0,+∞)减,x∈(-∞,0)减????
奇偶性
奇
偶
奇
非奇非偶
奇
公共点
都经过点⑥ (1,1)????
五个幂函数的性质
1.幂函数的图象都过点(0,0),(1,1).?(????? )
2.幂函数的图象一定不能出现在第四象限,但可能出现在第二象限.?( √ )
3.当幂指数α取1,3,?时,幂函数y=xα是增函数.( √ )
4.当幂指数α=-1时,幂函数y=xα在定义域上是减函数.?(????? )
5.当α=0时,幂函数y=xα的图象是一条直线.?(????? )
6.若幂函数y=xα的图象关于原点对称,则y=xα在定义域内y随x的增大而增大.?(?????
)
判断正误,正确的画“√”
,错误的画“
?”
.
如何把握幂函数的图象
解决幂函数图象问题应把握的两个原则
(1)根据幂函数在第一象限内的图象确定幂指数α(α>0)的大小关系.依据图象高低
判断幂指数的大小,相关结论如下:
①在x∈(0,1)上,指数越大,幂函数的图象越靠近x轴(简记为指大图低);
②在x∈(1,+∞)上,指数越大,幂函数的图象越远离x轴(简记为指大图高).
(2)利用定义域及奇偶性确定函数在其他象限的图象.
??
若点(?,2)在幂函数f(x)(x≠0)的图象上,点?在幂函数g(x)的图象上,问:当
x为何值时,
(1)f(x)>g(x)?(2)f(x)=g(x)?(3)f(x)
先由点在图象上确定幂函数的解析式,再由解析式得到大致图象,利用图象解决问
题.
解析????设f(x)=xα,因为点(?,2)在幂函数f(x)的图象上,所以将点(?,2)代入f(x)=xα中,
得2=(?)α,解得α=2,则f(x)=x2.同理,可求得g(x)=x-2.
在同一平面直角坐标系中作出幂函数f(x)=x2和g(x)=x-2的图象(如图所示).
?
观察图象可得:
(1)当x>1或x<-1时,
f(x)>g(x).
(2)当x=1或x=-1时,
f(x)=g(x).
(3)当-1
问题
1.是否存在同时满足(1)(2)的幂函数f(x)?
提示:因为m∈{m|-2
由①②③得m=0.因此存在同时满足(1)(2)的幂函数f(x).
2.若存在,如何求出f(x)的解析式,以及x∈[0,3]时f(x)的值域?
提示:由问题1知m=0,此时f(x)=x3,且在区间[0,3]上是增函数,所以当x∈[0,3]时,函数f
(x)的值域为[0,27].
如何运用幂函数的性质解决相关问题
?
幂函数的性质与参数α可以互相确定:
(1)幂函数y=xα中只有一个参数α,幂函数的所有性质都与α的取值有关,故可由α确定
幂函数的定义域、值域、单调性、奇偶性.
(2)反过来,也可由幂函数的性质去限制α的取值:
①利用幂函数的单调性求出α的取值范围;
②由奇偶性结合所给条件确定α的值.
??
已知幂函数y=x3m-9(m∈N
)的图象关于y轴对称,且y=x3m-9(m∈N
)在(0,+∞)上单
调递减,求满足?思路点拨
由幂函数的性质确定参数m的值,再由函数的单调性解不等式.
解析????因为函数y=x3m-9(m∈N
)在(0,+∞)上单调递减,所以3m-9<0,解得m<3.
又m∈N
,所以m=1或m=2.
因为幂函数y=x3m-9的图象关于y轴对称,所以3m-9为偶数,故m=1,则原不等式可化为
(a+1?<(3-2a?.
易知y=?在(-∞,0)和(0,+∞)上单调递减,且当x<0时,y<0,当x>0时,y>0,
所以a+1>3-2a>0或3-2a
??
比较下列各组数的大小.
(1)1.?,1.?;(2)(-1.2?,(-1.25?.
思路点拨
构造幂函数,利用幂函数的性质比较各组数的大小.
解析????(1)∵函数y=?在第一象限内单调递增,且1.5<1.7,∴1.?<1.?.
(2)∵(-1.2?=1.?,(-1.25?=1.2?,
且函数y=?在第一象限内单调递减,1.2<1.25,
∴1.?>1.2?,即(-1.2?>(-1.25?.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
