3.4 函数的应用(一) 课件(共22张PPT)
文档属性
| 名称 | 3.4 函数的应用(一) 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-28 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
人教版A版(2019)
必修第一册
3.4
函数的应用(一)
学习本节内容,能从具体实例中学会建立函数模型,利用函数模型解决实际问题.学
习时还应掌握以下几点:
1.理解函数模型是描述客观世界中变量关系和规律的重要数学语言和工具.
2.体会学习过的一次函数、二次函数、幂函数等一些基本函数模型的广泛运用.
3.体会利用常见的函数模型解决一些简单实际问题的过程与方法.
名称
解析式
条件
一次函数模型
①????y=kx+b????
②????k≠0????
反比例函数模型
y=?
③????k≠0????
二次函数模型
一般式:④????y=ax2+bx+c????
⑤????a≠0????
三类常见函数模型
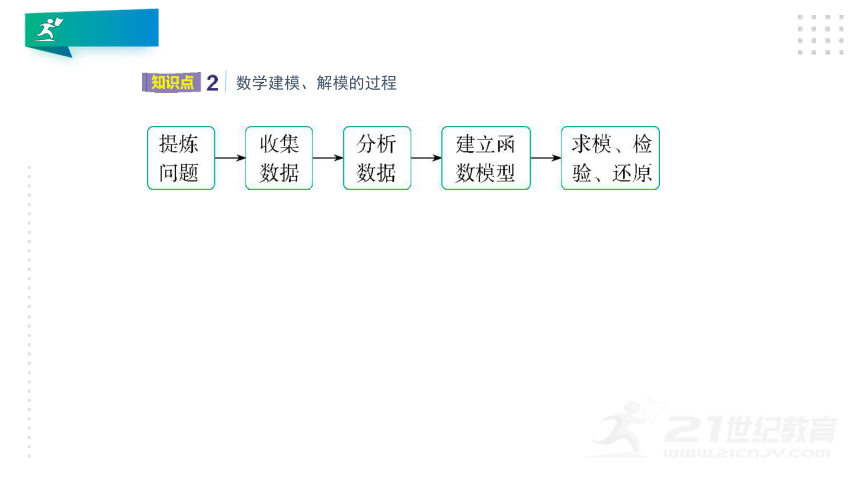
数学建模、解模的过程
1.一个好的函数模型,既能与现有数据高度符合,又能很好地推演和预测.?( √ )
2.用来拟合散点图的函数图象一定要经过所有点.?(????? )
3.当x每增加一个单位时,y增加或减少的量为定值,则y是x的一次函数.?( √ )
提示:当x每增加一个单位时,y增加或减少的量为定值,则其图象是直线,所以y是x的
一次函数.
4.在某种金属材料的耐高温实验中,温度y(℃)随着时间t(min)变化的情况由计算机
记录后显示的图象如图所示.
由图可知前5分钟温度增加越来越快.?(????? )
?
判断正误,正确的画“√”
,错误的画“
?”
.
?
在实际问题中,大多涉及的两个变量之间的关系符合已知函数模型,如一次函数(例
如:匀速直线运动的路程和时间的关系,弹簧的伸长量和拉力的关系等)、二次函
数、反比例函数、幂函数等,解决这种函数应用问题的常见步骤如下:
1.利用待定系数法求出函数解析式;
2.根据函数解析式,结合题中需要研究的函数的性质解决实际问题.
在函数模型中,二次函数模型占有重要的地位.在根据实际问题得到二次函数的解
析式后,可以利用配方法、换元法、函数的单调性等来求函数的最值,从而解决实
际问题中的利润最大、用料最省等问题.
??
如何解决已知函数模型的实际应用问题
投资A种商
品金额(万
元)
1
2
3
4
5
6
获纯利润(万
元)
0.65
1.39
1.85
2
1.84
1.40
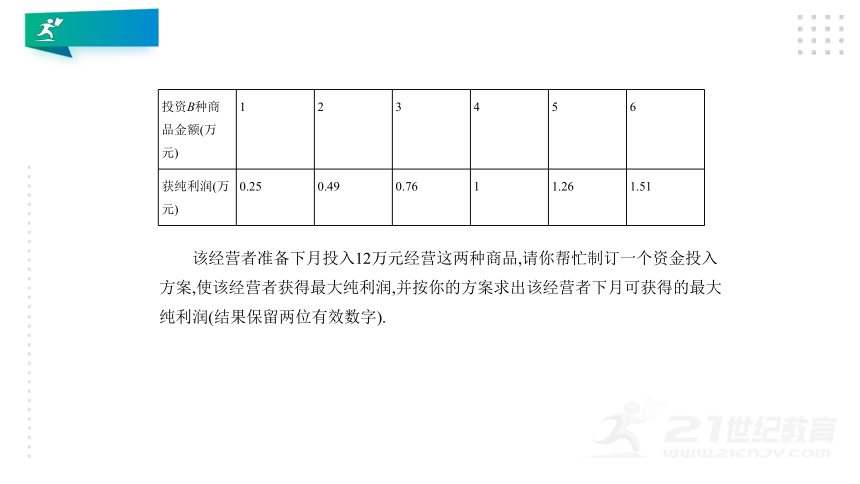
某个体经营者把开始六个月试销A,B两种商品的逐月投资与所获纯利润列成
下表:
投资B种商
品金额(万
元)
1
2
3
4
5
6
获纯利润(万
元)
0.25
0.49
0.76
1
1.26
1.51
该经营者准备下月投入12万元经营这两种商品,请你帮忙制订一个资金投入
方案,使该经营者获得最大纯利润,并按你的方案求出该经营者下月可获得的最大
纯利润(结果保留两位有效数字).
思路点拨
利用已知数据画出散点图,根据散点图的形状选择函数模型,结合条件求出函数的
解析式及定义域,最后由函数的解析式解决相关问题.
解析????以投资金额为横坐标,纯利润为纵坐标,在平面直角坐标系中画出散点图,如
图所示.
?
?
由散点图可以看出,A种商品所获纯利润y1(万元)与投资金额x(万元)之间的变化规
律可以用二次函数模型拟合.
取最高点(4,2),设y1=a(x-4)2+2(a≠0),把点(1,0.65)代入,得0.65=a(1-4)2+2,解得a=-0.1
5,所以y1=-0.15(x-4)2+2(0B种商品所获纯利润y2(万元)与投资金额x(万元)之间的变化规律可以用一次函数
模型进行拟合.
设y2=kx+b(k≠0),将点(1,0.25)和(4,1)代入,得?解得?所以y2=0.25x
(0设下个月投入A,B两种商品的资金分别为xA,xB(万元),获得的纯利润分别为yA,yB(万
元),总利润为W(万元),则xA+xB=12,
W=yA+yB=-0.15(xA-4)2+2+0.25xB,
所以W=-0.15?+?(0当xA=?≈3.2时,W取得最大值,约为4.1,此时xB=8.8,
即该经营者下个月把12万元中的3.2万元投入A种商品,8.8万元投入B种商品,可获
得最大纯利润,最大纯利润约为4.1万元.
某工厂在甲、乙两地的两个分厂分别生产了某种机器12台、6台,现销售给A
地10台,B地8台.已知从甲地调运一台机器至A地、B地的费用分别为400元、800
元,从乙地调运一台机器至A地、B地的费用分别为300元、500元.
问题
1.设从甲地调运x台机器至A地,能否确定这种机器的调配情况?
提示:能,甲地调运x台机器至A地,调运(12-x)台机器至B地;乙地调运(10-x)台机器至
A地,调运(x-4)台机器至B地.
2.若从甲地调运x台机器至A地,能否确定x的取值范围?
提示:能,根据实际意义得,x≥0,12-x≥0,10-x≥0,x-4≥0,且x∈N,解得4≤x≤10,且x
∈N.
如何解决未知函数模型的实际应用问题
3.设从甲地调运x台机器至A地,如何确定总费用y(元)关于台数x的函数解析式?
提示:依题意有y=400x+800(12-x)+300(10-x)+500(x-4)=-200x+10
600(4≤x≤10,且x
∈N).
4.若总运费不超过9
000元,如何确定有几种调运方案?
提示:令y≤9
000,可得x≥8,∵x∈[4,10]且x∈N,∴x的值为8或9或10.故有3种方案使
得总运费不超过9
000元.
5.如何确定总运费最低的调运方案及最低的总运费?
提示:y=-200x+10
600是减函数,x∈[4,10],且x∈N,由此可知当x=10时,总运费最低,
为8
600元.
调运方案:甲地调运10台至A地,调运2台至B地;乙地6台全调运至B地.
?
1.解决未知函数模型的实际问题时,主要抓住四点:“求什么,设什么,列什么,限制
什么”.
(1)“求什么”就是弄清楚要解决什么问题,完成什么任务,通常表现为求函数值.
(2)“设什么”就是弄清楚这个问题中有哪些变化因素,找出变化的根源,通常设变
化的根源为自变量.
(3)“列什么”就是从函数值出发逐步应用公式,用自变量与已知量表示函数值,直
至求出函数解析式.
(4)“限制什么”就是指自变量所应满足的限制条件,不仅要考虑自变量是否有意
义,还要考虑用自变量表示的其他所有量是否有意义,另外还要考虑变量的实际含
义,如整数解等.
2.建立函数模型解决实际问题的步骤:
(1)设恰当的变量:研究实际问题中量与量之间的关系,确定变量之间的关系,可用x,
y分别表示问题中的变量;
(2)建立函数模型:将变量y表示成x的函数,注意函数的定义域;
(3)求解函数模型;
(4)给出实际问题的解.
??
要在墙上开一个上部分为半圆,下部分为矩形的窗户(如图),在窗框为定长l的
条件下,要使窗户的透光面积S最大,窗户应具有怎样的尺寸?
?
思路点拨
选择适当的自变量与函数值,利用各量之间的关系求出函数的解析式与定义域,由
函数的解析式解决相关问题.
解析????由题意得窗框总长l=?x+x+2y,
∴y=?,
∴S=?x2+xy=?x2+x·?
=-??+?.
由?
可得x∈?.
所以当x=?时,S取得最大值,此时y=?.
所以当x=?,y=?时,窗户的透光面积最大.
解题时要注意求定义域时,不仅要使自变量表示的量有意义(如本题中x>0),还要使
用自变量表示的其他量有意义?,防止出现因定义域求错而导致解
题错误的情况.
?
商场销售某一品牌的羊毛衫,购买人数是羊毛衫标价的一次函数,标价越高,购
买人数越少.把购买人数为0时的标价称为无效价格,已知无效价格为每件300元.现
在这种羊毛衫的成本价是100元/件,商场以高于成本价的价格(标价)出售.
(1)若商场要获取最大利润,则羊毛衫的标价应定为每件多少元?
(2)通常情况下,获取最大利润只是一种理想结果,如果商场要获得理想最大利润的
75%,那么羊毛衫的标价应为每件多少元?
思路点拨
选择自变量与函数值?求出函数的解析式与定义域?利用函数知识解决实际
问题.
解析????(1)设购买人数为n,羊毛衫的标价为每件x元,利润为y元,则x∈(100,300],
可设n=kx+b,易知k<0,
由题意知0=300k+b,即b=-300k,∴n=k(x-300),
∴y=k(x-300)(x-100)=k(x-200)2-10
000k(x∈(100,300]).
∵k<0,∴当x=200时,y最大,ymax=-10
000k,即商场要获取最大利润,羊毛衫的标价应
定为每件200元.
(2)由题意及(1)知,k(x-100)(x-300)=-10
000k·75%,
化简得x2-400x+37
500=0,解得x=250或x=150.
∴商场要获得理想最大利润的75%,羊毛衫每件的标价应为250元或150元.
https://www.21cnjy.com/help/help_extract.php
人教版A版(2019)
必修第一册
3.4
函数的应用(一)
学习本节内容,能从具体实例中学会建立函数模型,利用函数模型解决实际问题.学
习时还应掌握以下几点:
1.理解函数模型是描述客观世界中变量关系和规律的重要数学语言和工具.
2.体会学习过的一次函数、二次函数、幂函数等一些基本函数模型的广泛运用.
3.体会利用常见的函数模型解决一些简单实际问题的过程与方法.
名称
解析式
条件
一次函数模型
①????y=kx+b????
②????k≠0????
反比例函数模型
y=?
③????k≠0????
二次函数模型
一般式:④????y=ax2+bx+c????
⑤????a≠0????
三类常见函数模型
数学建模、解模的过程
1.一个好的函数模型,既能与现有数据高度符合,又能很好地推演和预测.?( √ )
2.用来拟合散点图的函数图象一定要经过所有点.?(????? )
3.当x每增加一个单位时,y增加或减少的量为定值,则y是x的一次函数.?( √ )
提示:当x每增加一个单位时,y增加或减少的量为定值,则其图象是直线,所以y是x的
一次函数.
4.在某种金属材料的耐高温实验中,温度y(℃)随着时间t(min)变化的情况由计算机
记录后显示的图象如图所示.
由图可知前5分钟温度增加越来越快.?(????? )
?
判断正误,正确的画“√”
,错误的画“
?”
.
?
在实际问题中,大多涉及的两个变量之间的关系符合已知函数模型,如一次函数(例
如:匀速直线运动的路程和时间的关系,弹簧的伸长量和拉力的关系等)、二次函
数、反比例函数、幂函数等,解决这种函数应用问题的常见步骤如下:
1.利用待定系数法求出函数解析式;
2.根据函数解析式,结合题中需要研究的函数的性质解决实际问题.
在函数模型中,二次函数模型占有重要的地位.在根据实际问题得到二次函数的解
析式后,可以利用配方法、换元法、函数的单调性等来求函数的最值,从而解决实
际问题中的利润最大、用料最省等问题.
??
如何解决已知函数模型的实际应用问题
投资A种商
品金额(万
元)
1
2
3
4
5
6
获纯利润(万
元)
0.65
1.39
1.85
2
1.84
1.40
某个体经营者把开始六个月试销A,B两种商品的逐月投资与所获纯利润列成
下表:
投资B种商
品金额(万
元)
1
2
3
4
5
6
获纯利润(万
元)
0.25
0.49
0.76
1
1.26
1.51
该经营者准备下月投入12万元经营这两种商品,请你帮忙制订一个资金投入
方案,使该经营者获得最大纯利润,并按你的方案求出该经营者下月可获得的最大
纯利润(结果保留两位有效数字).
思路点拨
利用已知数据画出散点图,根据散点图的形状选择函数模型,结合条件求出函数的
解析式及定义域,最后由函数的解析式解决相关问题.
解析????以投资金额为横坐标,纯利润为纵坐标,在平面直角坐标系中画出散点图,如
图所示.
?
?
由散点图可以看出,A种商品所获纯利润y1(万元)与投资金额x(万元)之间的变化规
律可以用二次函数模型拟合.
取最高点(4,2),设y1=a(x-4)2+2(a≠0),把点(1,0.65)代入,得0.65=a(1-4)2+2,解得a=-0.1
5,所以y1=-0.15(x-4)2+2(0
模型进行拟合.
设y2=kx+b(k≠0),将点(1,0.25)和(4,1)代入,得?解得?所以y2=0.25x
(0
元),总利润为W(万元),则xA+xB=12,
W=yA+yB=-0.15(xA-4)2+2+0.25xB,
所以W=-0.15?+?(0
即该经营者下个月把12万元中的3.2万元投入A种商品,8.8万元投入B种商品,可获
得最大纯利润,最大纯利润约为4.1万元.
某工厂在甲、乙两地的两个分厂分别生产了某种机器12台、6台,现销售给A
地10台,B地8台.已知从甲地调运一台机器至A地、B地的费用分别为400元、800
元,从乙地调运一台机器至A地、B地的费用分别为300元、500元.
问题
1.设从甲地调运x台机器至A地,能否确定这种机器的调配情况?
提示:能,甲地调运x台机器至A地,调运(12-x)台机器至B地;乙地调运(10-x)台机器至
A地,调运(x-4)台机器至B地.
2.若从甲地调运x台机器至A地,能否确定x的取值范围?
提示:能,根据实际意义得,x≥0,12-x≥0,10-x≥0,x-4≥0,且x∈N,解得4≤x≤10,且x
∈N.
如何解决未知函数模型的实际应用问题
3.设从甲地调运x台机器至A地,如何确定总费用y(元)关于台数x的函数解析式?
提示:依题意有y=400x+800(12-x)+300(10-x)+500(x-4)=-200x+10
600(4≤x≤10,且x
∈N).
4.若总运费不超过9
000元,如何确定有几种调运方案?
提示:令y≤9
000,可得x≥8,∵x∈[4,10]且x∈N,∴x的值为8或9或10.故有3种方案使
得总运费不超过9
000元.
5.如何确定总运费最低的调运方案及最低的总运费?
提示:y=-200x+10
600是减函数,x∈[4,10],且x∈N,由此可知当x=10时,总运费最低,
为8
600元.
调运方案:甲地调运10台至A地,调运2台至B地;乙地6台全调运至B地.
?
1.解决未知函数模型的实际问题时,主要抓住四点:“求什么,设什么,列什么,限制
什么”.
(1)“求什么”就是弄清楚要解决什么问题,完成什么任务,通常表现为求函数值.
(2)“设什么”就是弄清楚这个问题中有哪些变化因素,找出变化的根源,通常设变
化的根源为自变量.
(3)“列什么”就是从函数值出发逐步应用公式,用自变量与已知量表示函数值,直
至求出函数解析式.
(4)“限制什么”就是指自变量所应满足的限制条件,不仅要考虑自变量是否有意
义,还要考虑用自变量表示的其他所有量是否有意义,另外还要考虑变量的实际含
义,如整数解等.
2.建立函数模型解决实际问题的步骤:
(1)设恰当的变量:研究实际问题中量与量之间的关系,确定变量之间的关系,可用x,
y分别表示问题中的变量;
(2)建立函数模型:将变量y表示成x的函数,注意函数的定义域;
(3)求解函数模型;
(4)给出实际问题的解.
??
要在墙上开一个上部分为半圆,下部分为矩形的窗户(如图),在窗框为定长l的
条件下,要使窗户的透光面积S最大,窗户应具有怎样的尺寸?
?
思路点拨
选择适当的自变量与函数值,利用各量之间的关系求出函数的解析式与定义域,由
函数的解析式解决相关问题.
解析????由题意得窗框总长l=?x+x+2y,
∴y=?,
∴S=?x2+xy=?x2+x·?
=-??+?.
由?
可得x∈?.
所以当x=?时,S取得最大值,此时y=?.
所以当x=?,y=?时,窗户的透光面积最大.
解题时要注意求定义域时,不仅要使自变量表示的量有意义(如本题中x>0),还要使
用自变量表示的其他量有意义?,防止出现因定义域求错而导致解
题错误的情况.
?
商场销售某一品牌的羊毛衫,购买人数是羊毛衫标价的一次函数,标价越高,购
买人数越少.把购买人数为0时的标价称为无效价格,已知无效价格为每件300元.现
在这种羊毛衫的成本价是100元/件,商场以高于成本价的价格(标价)出售.
(1)若商场要获取最大利润,则羊毛衫的标价应定为每件多少元?
(2)通常情况下,获取最大利润只是一种理想结果,如果商场要获得理想最大利润的
75%,那么羊毛衫的标价应为每件多少元?
思路点拨
选择自变量与函数值?求出函数的解析式与定义域?利用函数知识解决实际
问题.
解析????(1)设购买人数为n,羊毛衫的标价为每件x元,利润为y元,则x∈(100,300],
可设n=kx+b,易知k<0,
由题意知0=300k+b,即b=-300k,∴n=k(x-300),
∴y=k(x-300)(x-100)=k(x-200)2-10
000k(x∈(100,300]).
∵k<0,∴当x=200时,y最大,ymax=-10
000k,即商场要获取最大利润,羊毛衫的标价应
定为每件200元.
(2)由题意及(1)知,k(x-100)(x-300)=-10
000k·75%,
化简得x2-400x+37
500=0,解得x=250或x=150.
∴商场要获得理想最大利润的75%,羊毛衫每件的标价应为250元或150元.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
