《数据的分析》单元检测题(有答案)
文档属性
| 名称 | 《数据的分析》单元检测题(有答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 47.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-14 00:00:00 | ||
图片预览


文档简介
《数据的分析》单元检测题
一.选择题 (每小题4分,共40分)
1. 数据1,6,3,9,8的极差是
A.1 B.5 C.6 D.8
2. 在一次科技知识竞赛中,两组学生成绩统计如下表,通过计算可知两组的方差为=172,=256.下列说法①两组的平均数相同;②甲组学生成绩比乙组学生成绩稳定;③甲组成绩的众数>乙组成绩的众数;④两组成绩的中位数均为80,但成绩≥80的人数甲组比乙组多,从中位数来看,甲组成绩总体比乙组好;⑤成绩高于或等于90分的人数乙组比甲组多,高分段乙组成绩比甲组好.其中正确的共有
分数 50 60 70 80 90 100
人数 甲组 2 5 10 13 14 6
乙组 4 4 16 2 12 12
A.2种 B.3种 C.4种 D.5种
3. 从观察所得的数据中取出组成一个样本,那么这个样本的平均数是
A. B. C. D.
4. 为了解某校计算机等级考试的情况,抽取50名学生的计算机考试成绩进行了统计,统计结果如表所示,则这50名学生计算机考试成绩的众数、中位数分别是
考试分数(分) 1 20 2 16 3 12 4 8 5
人 数 24 28 5 3
A.20,16 B.16,20 C.20,12 D.16,12
5. 已知甲乙两组数据的平均数都是5,甲组数据的方差,乙组数据的方差则
A.甲组数据比乙组数据的波动大 B.乙组数据比甲组数据的波动大
C.甲组数据与乙组数据的波动一样大 D.甲乙两组数据的波动大小不能比较
6. 在样本方差的计算式中,数字10与20分别表示样本的
A.容量,方差 B.平均数,容量 C.容量,平均数 D.标准差,平均数
7. 3件衬衣的平均价格为15元,4条短裤的平均价格为10元,5双手套平均价格为3元,共花钱
A.28元 B.84元 C.100元 D.112.6元
8. 5个整数从小到的排列,其中位数是4,如果这组数据的唯一众数是6,则这5个整数最大的和可能是
A.21 B.22 C.23 D.24
9. 衡量一组数据波动大小的统计量是
A.平均数 B.众数 C.中位数 D.方差
10. 已知一组数据-2,-1,0,,1的平均数为0,那么这组数据的方差为
A.0 B.2 C.-2 D.10
第Ⅱ卷(非选择题 共8道填空题8道解答题)
请将你认为正确的答案代号填在下表中
二.简答题 (每小题3分,共24分)
11.
1 2 3 4 …
2 4 6 8 …
3 6 9 12 …
4 8 12 16 …
… … … … …
观察右表,依据表格数据排列的规律,数2 008在表格
中出现的次数共有_______次.
12. 为了缓解旱情,我市发射增雨火箭,实施增雨作业.在一场降雨中,某县测得10个面积相等区域的的降雨量如下
区 域 1 2 3 4 5 6 7 8 9 10
降雨量(mm) 10 12 13 13 20 15 14 15 14 14
则该县这个10个区域降雨量的众数为(mm);平均降雨量为(mm)
13. 如图4,是甲、乙两地5月下旬的日平均气温统计图,则甲、乙两地这10天日平均气温的方差大小关系为:_________.
14. 某中学规定学生的各科成绩满分为100分,其中平时成绩占10%,期中考试成绩占30%,期末考试成绩占60%,小美的数学成绩(百分制)依次是95分、85分、90分,小美这学期的数学成绩是分
15. 一个样本,各个数据的和为515,如果这样本的平均数为5,那么这个样本的容量是__________
16. 某班一组男生参加体育测试,引体向上成绩(单位:个)如下:6,9,11,13,11,7,10,8,12这组男生成绩的众数是________;中位数是________.
17. 现有甲、乙两支球队,每支球队队员身高数据的平均数均为1.70米,方差分别为= 0.28、= 0.36,则身高较整齐的球队是 队(填“甲”或“乙”)
18. 为了判断甲、乙两个班级学生参加英语口语测试成绩哪一个班比较整齐,通常需要比较两个班级成绩的_________________________
三.解答题 (共56分)
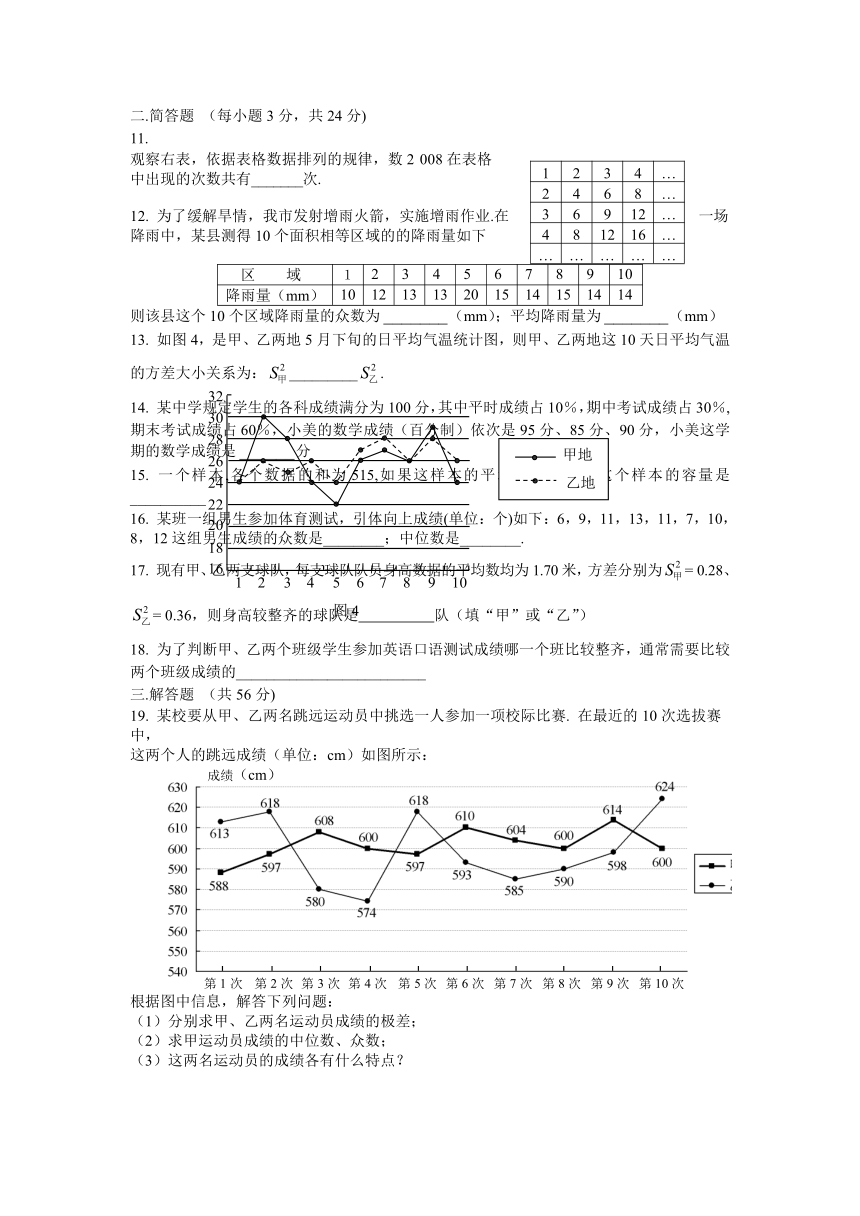
19. 某校要从甲、乙两名跳远运动员中挑选一人参加一项校际比赛. 在最近的10次选拔赛中,
这两个人的跳远成绩(单位:cm)如图所示:
根据图中信息,解答下列问题:
(1)分别求甲、乙两名运动员成绩的极差;
(2)求甲运动员成绩的中位数、众数;
(3)这两名运动员的成绩各有什么特点?
20. 某中学为了了解全校的耗电情况,抽查了10天中全校每天的耗电量,数据如下表:
度数 90 93 102 113 114 120
天数 1 1 2 3 1 2
(1)写出上表中数据的众数和平均数.
(2)根据上题获得的数据,估计该校一个月的耗电量(按30天计算).
(3)若当地每度电的价格是0. 5元,写出该校应付电费y(元)与天数x(x取正整数,单位:天)的函数关系式.
21. 甲、乙、丙三个家电厂家在广告中都声称,他们的某种电子产品在正常情况下的使用寿命都是8年,经质量检测部门对这三家销售的产品的使用寿命进行跟踪调查,统计结果如下(单位:年):
甲厂:4,5,5,5,5,7,9,12,13,15;
乙厂:6,6,8,8,8,9,10,12,14,15;
丙厂:4,4,4,6,7,9,13,15,16,16.
请回答下列问题:
(1)分别写出以上三组数据的平均数、众数、中位数;
(2)这三个厂家的推销广告分别用了哪一种表示集中趋势的特征数?
(3)如果你是顾客,宜选购哪家工厂的产品?为什么?
22. 某市对九年级学生进行了一次学业水平测试,成绩评定分A、B、C、D四个等第.为了解这次数学测试成绩情况,相关部门从该市的农村、县镇、城市三类群体的学生中共抽取2 000名学生的数学成绩进行统计分析,相应数据的统计图表如下:
(1)请将上面表格中缺少的三个数据补充完整;
(2)若该市九年级共有60 000名学生参加测试,试估计该市学生成绩合格以上(含合格)的人数.
23. 某公司欲聘请一位员工,三名应聘者甲,乙,丙的原始评分如下表:
项目 原始评分 应聘者 仪表 工作经验 电脑操作 社交能力 工作效率
甲 4 5 5 3 3
乙 4 3 3 4 4
丙 3 3 4 4 5
(1)如果按五项原始评分的平均分评分,谁被聘用?
(2)如果按仪表,工作经验,电脑操作,社交能力,工作效率繁荣原始评分分别占10%,15%,20%,25%,30%综合评分,谁将被聘用?
24. 利用计算器计算下列数据的平均数:
(1)9. 48,9. 46,9. 43,9. 49,9. 47,9. 45,9. 44,9. 42,9. 47,9. 46
(2)某工人在30天中加工一种零件的日产量为2天51件,3天52件,6天53件,8天54件,7天55件,3天56件,1天59件,求这个工人平均每天加工零件多少件?
25. 为了从甲,乙两名学生中选拔一个参加今年六月份的全县中学生数学竞赛,每个月对他们的学进行一次测验,图中是两人赛前5次测验成绩的折线统计图.
(1)分别求出甲,乙两名学生5次测验成绩的平均数句方差.
(2)如果你是他们的辅导老师,应选派哪一名学生参加这次数学竞赛.你结合所学统计知识说明理由
26. 某学校对初中毕业班经过初步比较后,决定从初三(1)、(4)、(8)班这三个班中推荐一个班为市级先进班集体的候选班.现对这三个班进行综合素质考评,下表是它们五项素质考评的得分表(以分为单位,每项满分为10分).
班级 行为规范 学习成绩 校运动会 艺术获奖 劳动卫生
初三(1)班 10 10 6 10 7
初三(4)班 10 8 8 9 8
初三(8)班 9 10 9 6 9
(1)请问各班五项考评分的平均数、中位数和众数中哪个统计量不能反映三个班的考评结果的差异?并从中选择一个能反映差异的统计量将他们得分进行排序;
(2)根据你对表中五个项目的重要程度的认识,设定一个各项考评内容的占分比例(比例的各项须满足:①均为整数;②总和为10;③不全相同),按这个比例对各班的得分重新计算,比较出大小关系,并从中推荐一个得分最高的班级作为市级先进班集体的候选班.
第( )单元检测题参考答案(仅供参考)
1 2 3 4 5 6 7 8 9 10
D D D A B C C A D B
1. [解析]本题考查了极差的概念.根据极差的定义可知这几个数的极差为8.故撂除A、B、C选项,选D
二.简答题答案:
11. 8
12. 14;14
13.
14. 89
15.
16. 11 10
17. 甲
18. 方差
三.解答题答案:
19. (1)甲、乙两名运动员成绩的极差分别为26 cm,50 cm. ……………………………2分
(2)甲的中位数是600 cm,众数是600 cm. …………………………………………6分
(3)答案不惟一,如:甲的成绩比较稳定,波动小;乙成绩不稳定,波动较大. …8分
20. (1)众数为113度 平均数为108度
(2)某月耗电量Q=108×30=3240(度)
(3)y=0. 5×108x,∴y=54x
21. (1)甲厂:8,5,6;乙厂:9. 6,8,8. 5;丙厂:9. 4,4,8
(2)甲厂选用平均数8;乙厂选用众数8;丙厂选用中位数8
(3)宜选购乙厂的产品,因为乙厂产品平均使用寿命最长且多数超过8年或达到8年寿命.
22. (1)280,48,180. (3分)
(2)抽取的学生中,成绩不合格的人数共有,
所以成绩合格以上的人数为,
估计该市成绩合格以上的人数为.
答:估计该市成绩合格以上的人数约为54720人.
23. (1)三名应聘者的平均分分别为:4、3.6、3.8,所以甲将被聘用 (2)按综合平分。三人的得分情况是3.8、3.65、4.05,所以丙将被聘用
24. (1)9. 46 (2)54
25. (1), , (2)①甲最近2次的成绩不低于乙;②甲最近3次的成绩直线上升,而乙的成绩有所下降.所以,应选甲参加数学竞赛
26. (1)设P1、P4、P8顺次为3个班考评分的平均数;
W1、W4、W8顺次为3个班考评分的中位数;
Z1、Z4、Z8 顺次为3个班考评分的众数.
则:P1=(10+10+6+10+7)=8.6分),
P4=(8+8+8+9+10)=8.6(分),
P8=(9+10+9+6+9)=8.6(分).
W1=10(分),W4=8(分),W8=9(分).
(Z1=10(分),Z4=8(分),Z8=9(分)).
∴平均数不能反映这3个班的考评结果的差异,而用中位数(或众数)能反映差异,
且W1>W8>W4(Z1>Z8>Z4).
(2)(给出一种参考答案)选定:
行为规范:学习成绩:校运动会:艺术获奖:劳动卫生=3:2:3:1:1
设K1、K4、K8顺次为3个班的考评分,则:
K1=0.3×10+0.2×10+0.3×6+0.1×10+0.1×7=8.5,
K4=0.3×10+0.2×8+0.3×8+0.1×9+0.1×8=8.7,
K8=0.3×9+0.2×10+0.3×9+0.1×6+0.1×9=8.9.
∵K8>K4图4
1
2
3
4
5
6
7
8
9
10
16
18
20
22
24
26
28
30
32
乙地
甲地
成绩(cm)
第1次 第2次 第3次 第4次 第5次 第6次 第7次 第8次 第9次 第10次
30%
30%
40%
农村
县镇
城市
各类学生人数比例统计图
等第人数类别 A B C D
农村 ▲ 200 240 80
县镇 290 132 130 ▲
城市 240 ▲ 132 48
(注:等第A、B、C、D分别代表优秀、良好、合格、不合格)
各类学生成绩人数比例统计表
成绩(分)
100
95
90
85
80
75
70
65
60
一月 二月 三月 四月 五月 月份
一.选择题 (每小题4分,共40分)
1. 数据1,6,3,9,8的极差是
A.1 B.5 C.6 D.8
2. 在一次科技知识竞赛中,两组学生成绩统计如下表,通过计算可知两组的方差为=172,=256.下列说法①两组的平均数相同;②甲组学生成绩比乙组学生成绩稳定;③甲组成绩的众数>乙组成绩的众数;④两组成绩的中位数均为80,但成绩≥80的人数甲组比乙组多,从中位数来看,甲组成绩总体比乙组好;⑤成绩高于或等于90分的人数乙组比甲组多,高分段乙组成绩比甲组好.其中正确的共有
分数 50 60 70 80 90 100
人数 甲组 2 5 10 13 14 6
乙组 4 4 16 2 12 12
A.2种 B.3种 C.4种 D.5种
3. 从观察所得的数据中取出组成一个样本,那么这个样本的平均数是
A. B. C. D.
4. 为了解某校计算机等级考试的情况,抽取50名学生的计算机考试成绩进行了统计,统计结果如表所示,则这50名学生计算机考试成绩的众数、中位数分别是
考试分数(分) 1 20 2 16 3 12 4 8 5
人 数 24 28 5 3
A.20,16 B.16,20 C.20,12 D.16,12
5. 已知甲乙两组数据的平均数都是5,甲组数据的方差,乙组数据的方差则
A.甲组数据比乙组数据的波动大 B.乙组数据比甲组数据的波动大
C.甲组数据与乙组数据的波动一样大 D.甲乙两组数据的波动大小不能比较
6. 在样本方差的计算式中,数字10与20分别表示样本的
A.容量,方差 B.平均数,容量 C.容量,平均数 D.标准差,平均数
7. 3件衬衣的平均价格为15元,4条短裤的平均价格为10元,5双手套平均价格为3元,共花钱
A.28元 B.84元 C.100元 D.112.6元
8. 5个整数从小到的排列,其中位数是4,如果这组数据的唯一众数是6,则这5个整数最大的和可能是
A.21 B.22 C.23 D.24
9. 衡量一组数据波动大小的统计量是
A.平均数 B.众数 C.中位数 D.方差
10. 已知一组数据-2,-1,0,,1的平均数为0,那么这组数据的方差为
A.0 B.2 C.-2 D.10
第Ⅱ卷(非选择题 共8道填空题8道解答题)
请将你认为正确的答案代号填在下表中
二.简答题 (每小题3分,共24分)
11.
1 2 3 4 …
2 4 6 8 …
3 6 9 12 …
4 8 12 16 …
… … … … …
观察右表,依据表格数据排列的规律,数2 008在表格
中出现的次数共有_______次.
12. 为了缓解旱情,我市发射增雨火箭,实施增雨作业.在一场降雨中,某县测得10个面积相等区域的的降雨量如下
区 域 1 2 3 4 5 6 7 8 9 10
降雨量(mm) 10 12 13 13 20 15 14 15 14 14
则该县这个10个区域降雨量的众数为(mm);平均降雨量为(mm)
13. 如图4,是甲、乙两地5月下旬的日平均气温统计图,则甲、乙两地这10天日平均气温的方差大小关系为:_________.
14. 某中学规定学生的各科成绩满分为100分,其中平时成绩占10%,期中考试成绩占30%,期末考试成绩占60%,小美的数学成绩(百分制)依次是95分、85分、90分,小美这学期的数学成绩是分
15. 一个样本,各个数据的和为515,如果这样本的平均数为5,那么这个样本的容量是__________
16. 某班一组男生参加体育测试,引体向上成绩(单位:个)如下:6,9,11,13,11,7,10,8,12这组男生成绩的众数是________;中位数是________.
17. 现有甲、乙两支球队,每支球队队员身高数据的平均数均为1.70米,方差分别为= 0.28、= 0.36,则身高较整齐的球队是 队(填“甲”或“乙”)
18. 为了判断甲、乙两个班级学生参加英语口语测试成绩哪一个班比较整齐,通常需要比较两个班级成绩的_________________________
三.解答题 (共56分)
19. 某校要从甲、乙两名跳远运动员中挑选一人参加一项校际比赛. 在最近的10次选拔赛中,
这两个人的跳远成绩(单位:cm)如图所示:
根据图中信息,解答下列问题:
(1)分别求甲、乙两名运动员成绩的极差;
(2)求甲运动员成绩的中位数、众数;
(3)这两名运动员的成绩各有什么特点?
20. 某中学为了了解全校的耗电情况,抽查了10天中全校每天的耗电量,数据如下表:
度数 90 93 102 113 114 120
天数 1 1 2 3 1 2
(1)写出上表中数据的众数和平均数.
(2)根据上题获得的数据,估计该校一个月的耗电量(按30天计算).
(3)若当地每度电的价格是0. 5元,写出该校应付电费y(元)与天数x(x取正整数,单位:天)的函数关系式.
21. 甲、乙、丙三个家电厂家在广告中都声称,他们的某种电子产品在正常情况下的使用寿命都是8年,经质量检测部门对这三家销售的产品的使用寿命进行跟踪调查,统计结果如下(单位:年):
甲厂:4,5,5,5,5,7,9,12,13,15;
乙厂:6,6,8,8,8,9,10,12,14,15;
丙厂:4,4,4,6,7,9,13,15,16,16.
请回答下列问题:
(1)分别写出以上三组数据的平均数、众数、中位数;
(2)这三个厂家的推销广告分别用了哪一种表示集中趋势的特征数?
(3)如果你是顾客,宜选购哪家工厂的产品?为什么?
22. 某市对九年级学生进行了一次学业水平测试,成绩评定分A、B、C、D四个等第.为了解这次数学测试成绩情况,相关部门从该市的农村、县镇、城市三类群体的学生中共抽取2 000名学生的数学成绩进行统计分析,相应数据的统计图表如下:
(1)请将上面表格中缺少的三个数据补充完整;
(2)若该市九年级共有60 000名学生参加测试,试估计该市学生成绩合格以上(含合格)的人数.
23. 某公司欲聘请一位员工,三名应聘者甲,乙,丙的原始评分如下表:
项目 原始评分 应聘者 仪表 工作经验 电脑操作 社交能力 工作效率
甲 4 5 5 3 3
乙 4 3 3 4 4
丙 3 3 4 4 5
(1)如果按五项原始评分的平均分评分,谁被聘用?
(2)如果按仪表,工作经验,电脑操作,社交能力,工作效率繁荣原始评分分别占10%,15%,20%,25%,30%综合评分,谁将被聘用?
24. 利用计算器计算下列数据的平均数:
(1)9. 48,9. 46,9. 43,9. 49,9. 47,9. 45,9. 44,9. 42,9. 47,9. 46
(2)某工人在30天中加工一种零件的日产量为2天51件,3天52件,6天53件,8天54件,7天55件,3天56件,1天59件,求这个工人平均每天加工零件多少件?
25. 为了从甲,乙两名学生中选拔一个参加今年六月份的全县中学生数学竞赛,每个月对他们的学进行一次测验,图中是两人赛前5次测验成绩的折线统计图.
(1)分别求出甲,乙两名学生5次测验成绩的平均数句方差.
(2)如果你是他们的辅导老师,应选派哪一名学生参加这次数学竞赛.你结合所学统计知识说明理由
26. 某学校对初中毕业班经过初步比较后,决定从初三(1)、(4)、(8)班这三个班中推荐一个班为市级先进班集体的候选班.现对这三个班进行综合素质考评,下表是它们五项素质考评的得分表(以分为单位,每项满分为10分).
班级 行为规范 学习成绩 校运动会 艺术获奖 劳动卫生
初三(1)班 10 10 6 10 7
初三(4)班 10 8 8 9 8
初三(8)班 9 10 9 6 9
(1)请问各班五项考评分的平均数、中位数和众数中哪个统计量不能反映三个班的考评结果的差异?并从中选择一个能反映差异的统计量将他们得分进行排序;
(2)根据你对表中五个项目的重要程度的认识,设定一个各项考评内容的占分比例(比例的各项须满足:①均为整数;②总和为10;③不全相同),按这个比例对各班的得分重新计算,比较出大小关系,并从中推荐一个得分最高的班级作为市级先进班集体的候选班.
第( )单元检测题参考答案(仅供参考)
1 2 3 4 5 6 7 8 9 10
D D D A B C C A D B
1. [解析]本题考查了极差的概念.根据极差的定义可知这几个数的极差为8.故撂除A、B、C选项,选D
二.简答题答案:
11. 8
12. 14;14
13.
14. 89
15.
16. 11 10
17. 甲
18. 方差
三.解答题答案:
19. (1)甲、乙两名运动员成绩的极差分别为26 cm,50 cm. ……………………………2分
(2)甲的中位数是600 cm,众数是600 cm. …………………………………………6分
(3)答案不惟一,如:甲的成绩比较稳定,波动小;乙成绩不稳定,波动较大. …8分
20. (1)众数为113度 平均数为108度
(2)某月耗电量Q=108×30=3240(度)
(3)y=0. 5×108x,∴y=54x
21. (1)甲厂:8,5,6;乙厂:9. 6,8,8. 5;丙厂:9. 4,4,8
(2)甲厂选用平均数8;乙厂选用众数8;丙厂选用中位数8
(3)宜选购乙厂的产品,因为乙厂产品平均使用寿命最长且多数超过8年或达到8年寿命.
22. (1)280,48,180. (3分)
(2)抽取的学生中,成绩不合格的人数共有,
所以成绩合格以上的人数为,
估计该市成绩合格以上的人数为.
答:估计该市成绩合格以上的人数约为54720人.
23. (1)三名应聘者的平均分分别为:4、3.6、3.8,所以甲将被聘用 (2)按综合平分。三人的得分情况是3.8、3.65、4.05,所以丙将被聘用
24. (1)9. 46 (2)54
25. (1), , (2)①甲最近2次的成绩不低于乙;②甲最近3次的成绩直线上升,而乙的成绩有所下降.所以,应选甲参加数学竞赛
26. (1)设P1、P4、P8顺次为3个班考评分的平均数;
W1、W4、W8顺次为3个班考评分的中位数;
Z1、Z4、Z8 顺次为3个班考评分的众数.
则:P1=(10+10+6+10+7)=8.6分),
P4=(8+8+8+9+10)=8.6(分),
P8=(9+10+9+6+9)=8.6(分).
W1=10(分),W4=8(分),W8=9(分).
(Z1=10(分),Z4=8(分),Z8=9(分)).
∴平均数不能反映这3个班的考评结果的差异,而用中位数(或众数)能反映差异,
且W1>W8>W4(Z1>Z8>Z4).
(2)(给出一种参考答案)选定:
行为规范:学习成绩:校运动会:艺术获奖:劳动卫生=3:2:3:1:1
设K1、K4、K8顺次为3个班的考评分,则:
K1=0.3×10+0.2×10+0.3×6+0.1×10+0.1×7=8.5,
K4=0.3×10+0.2×8+0.3×8+0.1×9+0.1×8=8.7,
K8=0.3×9+0.2×10+0.3×9+0.1×6+0.1×9=8.9.
∵K8>K4
1
2
3
4
5
6
7
8
9
10
16
18
20
22
24
26
28
30
32
乙地
甲地
成绩(cm)
第1次 第2次 第3次 第4次 第5次 第6次 第7次 第8次 第9次 第10次
30%
30%
40%
农村
县镇
城市
各类学生人数比例统计图
等第人数类别 A B C D
农村 ▲ 200 240 80
县镇 290 132 130 ▲
城市 240 ▲ 132 48
(注:等第A、B、C、D分别代表优秀、良好、合格、不合格)
各类学生成绩人数比例统计表
成绩(分)
100
95
90
85
80
75
70
65
60
一月 二月 三月 四月 五月 月份
