11.3 探索三角形全等的条件

(共23张PPT)
11.3 探索三角形全等的条件
没有谁能够随随便便成功！
什么叫全等三角形？
两个能完全重合的三角形叫做全等三角形。
全等三角形的对应边、对应角有什么重要性质？
全等三角形的对应边相等，对应角相等。
如何判断两个三角形是全等三角形
两边和它们的夹角对应相等的两个三角形全等，简写成“边角边”或“SAS”
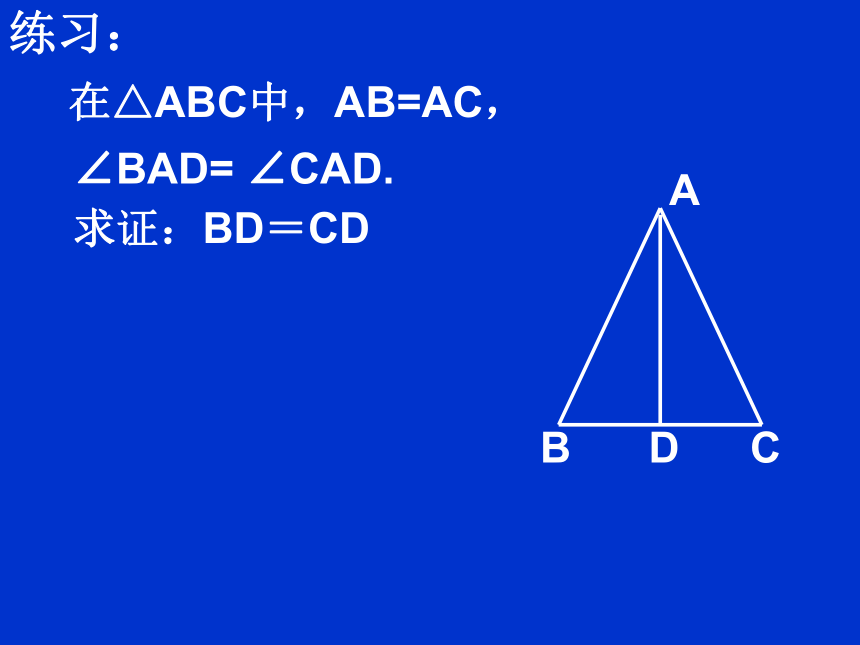
练习：
D
C
B
A
在△ABC中，AB=AC，
∠BAD= ∠CAD.
求证：BD＝CD
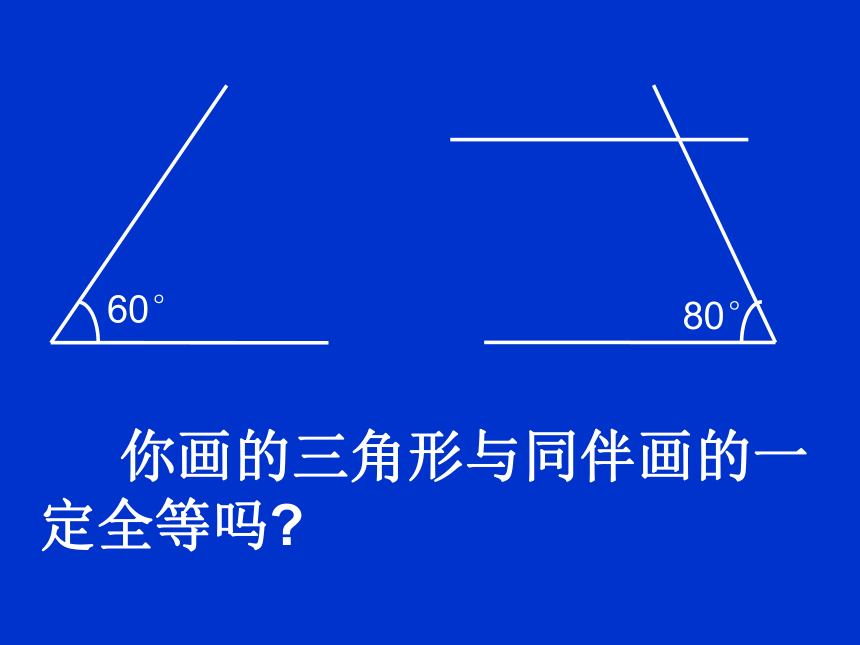
有两个角和它们的夹边对应相等的两个三角形一定全等吗？
研究下面的两个三角形：
\\
\\
做一做
若三角形的两个内角分别是60°和80°它们所夹的边为4cm,你能画出这个三角形吗
4cm
60°
80°
你画的三角形与同伴画的一定全等吗
60°
80°
两角和它们的夹边对应相等的两个三角形全等，简写成“角边角”或“ASA”
判定方法2
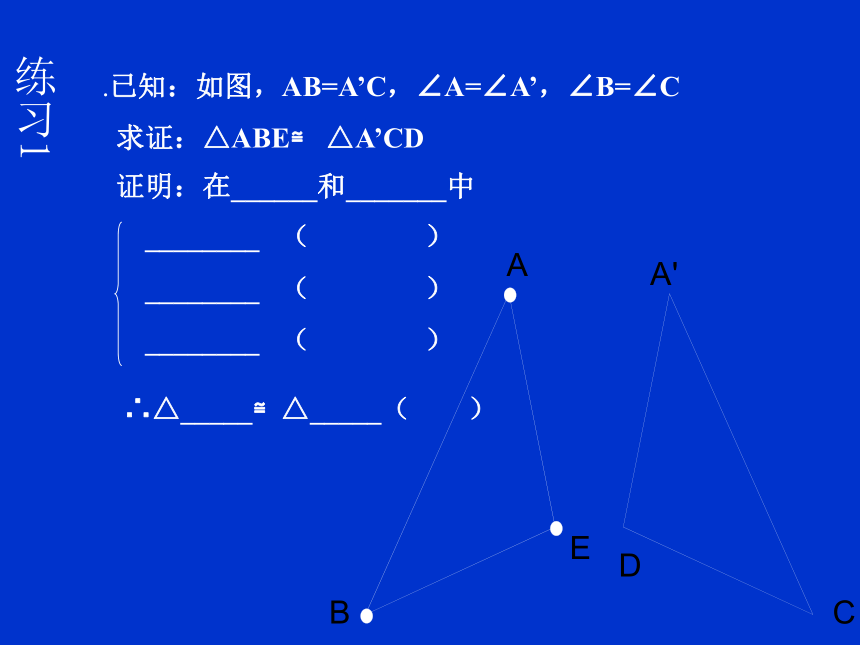
.已知：如图，AB=A’C，∠A=∠A’，∠B=∠C
求证：△ABE≌ △A’CD
________ （ ）
________ （ ）
________ （ ）
证明：在______和_______中
∴△_____≌△_____（ ）
练习1
例题讲解：
已知：点D在AB上，点E在AC上，BE和CD相交于点O，AB=AC，∠B=∠C。
求证：BD=CE
例1.
证明 ：在△ADC和△AEB中
∠A=∠A（公共角）
AC=AB（已知）
∠C=∠B（已知）
∴△ACD≌△ABE（ASA）
∴AD=AE（全等三角形的对应边相等）
又∵AB=AC（已知）
∴BD=CE
巩固练习
1.如图，∠1=∠2，∠3=∠4
求证：AC=AD
证明：∵∠____=180－∠3
　∠____=180－∠4
　　　而∠3=∠4（已知）
　　　∴∠ABD=∠ABC
　　　在△____和△____中
　　　——（ ）
　　　—— （ ）
　　　—— （ ） 　
　　　∴△____≌ △_____（ ）
∴AC=BD （全等三角形对应边相等）
2
1
4
3
已知，如图，∠1=∠2，∠C=∠D
求证：AC=AD
1
2
若三角形的两个内角分别是60°和40°，且40°所对的边为4cm，你能画出这个三角形吗
60°
40°
做一做
60°
40°
80°
你画的三角形与同伴画的一定全等吗
两角和其中一角的对边对应相等的两个三角形全等，简写成“角角边”或“AAS”
判定方法3
已知，如图，∠1=∠2，∠C=∠D
求证：AC=AD
1
2
练一练：
1、完成下列推理过程：
在△ABC和△DCB中，
∠ABC=∠DCB
∵ BC=CB
∴△ABC≌△DCB（ ）
ASA
A
B
C
D
O
1
2
3
4
∠2=∠1
AAS
∠3＝∠4
∠2＝∠1
CB＝BC
2、请在下列空格中填上适当的条件，使△ABC≌△DEF。
∵在△ABC和△DEF中
∴△ABC ≌△DEF（ ）
A
B
C
D
E
F
想一想：
如图，O是AB的中点，∠A=∠B，△AOC与△BOD全等吗？为什么？
A
B
C
D
O
我的思考过程如下：两角与夹边对应相等
∴△AOC≌△BOD
B
C
D
E
A
如图：已知AB＝AC，∠B＝∠C，△ABD与△ACE全等吗？为什么？
∴△ABD≌△ACE（ASA）
AE＝AD，∠B＝∠C，
∠B＝∠C
∠A＝∠A
AD＝AE
AAS
A
B
C
D
E
1
2
　　如图，已知　　　∠C＝∠E，∠1＝∠2，AB＝AD，△ABC和△ADE全等吗？为什么？
解： △ABC和△ADE全等。　　　　∵∠1＝∠2（已知）　　　　　　　　　∴∠1＋∠DAC＝∠2＋∠DAC　　　　　即∠BAC＝∠DAE　在△ABC和△ADC 中　　　　　　
∴ △ABC≌△ADE
（AAS）
小 结
1、知道ASA与AAS的联系与区别；
2、注意书写的格式以及推理的步骤：
（找— 列— 推）
3、学会寻找欠缺的条件
作业：
P113-114习题