11.3探索三角形全等的条件（1）

(共17张PPT)
11.3探索三角形全等的条件（1）
—SAS（边角边）
学会对自己负责，学会把自己管理成为最优秀的，需要外力强制，更需要内心的憧憬和不懈的努力。
什么叫全等三角形？
两个能完全重合的三角形叫做全等三角形。
全等三角形的对应边、对应角有什么重要性质？
全等三角形的对应边相等，对应角相等。
已知△ABC≌ △A’B’C’， △ABC的周长
为10cm，AB=3cm，BC=4cm，则：
A’B’= cm,B’C’= cm ,A’C’= cm.
3
4
3
　　(1)当两个三角形只有1组边或角相等时，它们全等吗？
　　(2)当两个三角形有2组边或角相等时，它们全等吗？
两个三角形，需要有多少组边或角对应相等时，才一定会全等呢？
（一个角对应相等）
—
—
（一条边对应相等）
//
//
（两条边对应相等）
（两个角对应相等）
一个角对应相等的两个三角形不一定全等；
一条边对应相等的两个三角形不一定全等；
两个角对应相等的两个三角形不一定全等；
两条边对应相等的两个三角形不一定全等；
一个角和一条边对应相等的两个三角形不一定全等；
\\
\\
(一个角、一条边对应相等）
=
=
①
②
可见：要使两个三角形全等应有3个
元素对应相等．
三角形共有6个元素(3条边、3个角)
共有4种情况
两边一角
两角一边
边边边
角角角
两边和它的夹角
两边和它一边的对角
两角和夹边
两角和一角的对边
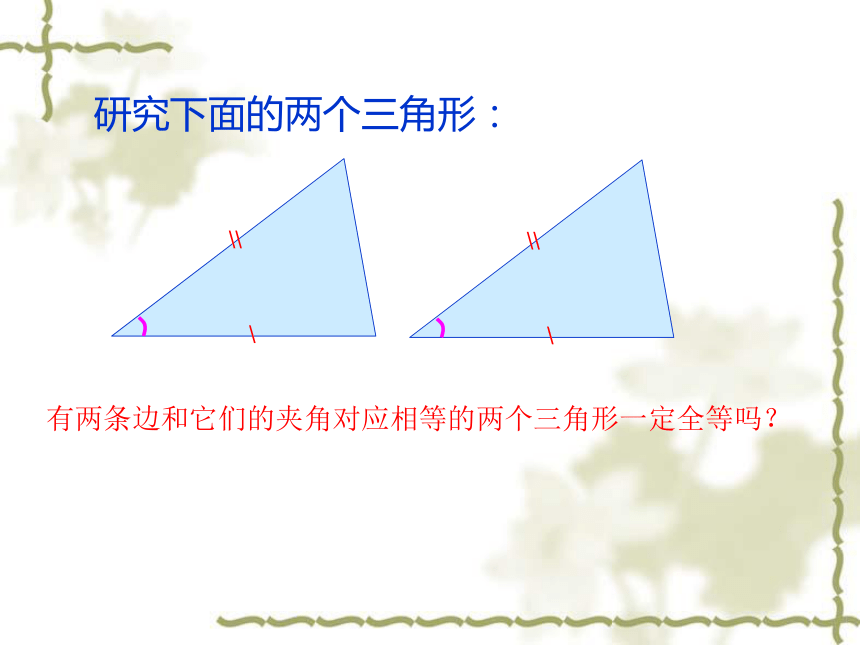
有两条边和它们的夹角对应相等的两个三角形一定全等吗？
研究下面的两个三角形：
\\
\
\\
\
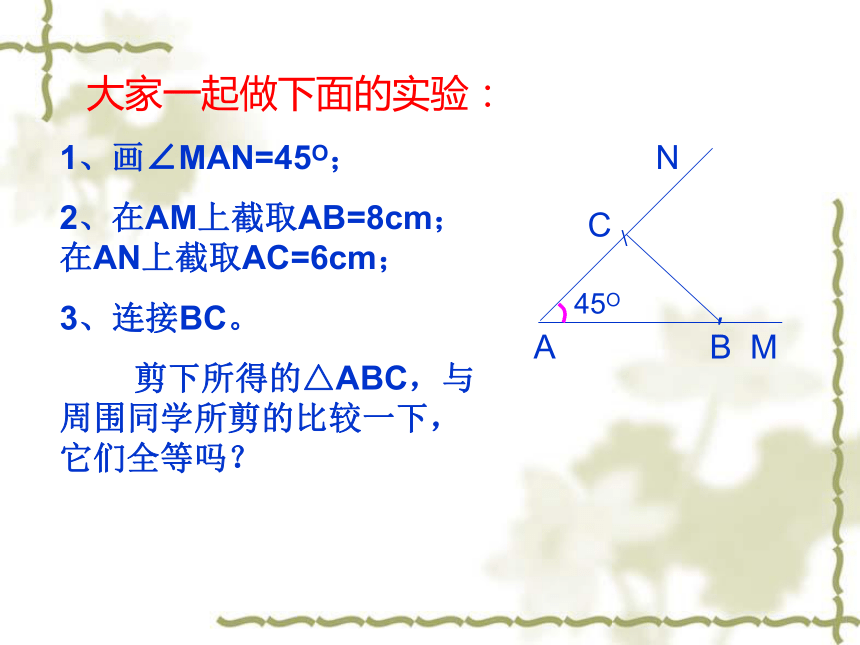
大家一起做下面的实验：
1、画∠MAN=45O；
2、在AM上截取AB=8cm；在AN上截取AC=6cm；
3、连接BC。
剪下所得的△ABC，与周围同学所剪的比较一下，它们全等吗？
B
C
A
M
N
45O
′
\
两边和它们的夹角对应相等的两个三角形全等，简写成“边角边”或“SAS”
\\
\
A
B
C
\\
\
D
E
F
在△ABC和△ DEF中，
因为AB=DE，∠B=∠E，BC=EF，
根据“SAS”可以得到△ABC≌△DEF
A
B
C
45°
1.5
3
45°
3
1.5
P
M
N
60°
D
E
F
3
1.5
③
①
②
　　观察下图中的三角形，猜一猜，
哪两个三角形是全等三角形？
如图：AB=AD，∠BAC= ∠DAC，△ABC和△ADC全等吗？为什么？
A
D
C
B
△ABC≌ △ADC，
因为AB=AD∠BAC=∠DAC，AC=AC，
根据“SAS”，可以得到△ABC≌ △ADC，
1、如图：AB=AC，AD=AE，△ABE和△ACD全等吗？请说明理由。
△ABE≌ △ACD，
因为AB=AC∠BAE=∠CAD，AE=AD，
根据“SAS”，可以得到△ABE≌ △ACD，
A
E
D
C
B
在这个图形中你还能得到哪些相等的线段和相等的角？
　　2.如图线段AB是一个池塘的长度，现在想测量这个池塘的长度，在水上测量不方便，你有什么好的方法较方便地把池塘的长度测量出来吗？想想看．
A
B
　　小明的设计方案：先在池塘旁取一个能直接到达A和B处的点C，连结AC并延长至D点，使AC=DC，连结BC并延长至E点，使BC=EC，连结CD，用米尺测出DE的长，这个长度就等于A，B两点的距离．请你说明理由．
E
C
A
D
B
B
E
C
A
D
AC=DC
∠ACB=∠DCE
BC=EC
∴AB=DE
∴△ACB≌△DCE(SAS)
在△ACB≌△DCE中
　　这节 课你学到了什么？
课时作业：P111-112