湖南省常德市澧县2020-2021学年八年级下学期期中数学试题(Word版 含解析)
文档属性
| 名称 | 湖南省常德市澧县2020-2021学年八年级下学期期中数学试题(Word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 594.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-29 07:07:28 | ||
图片预览

文档简介
湖南省常德市澧县2020-2021学年八年级下学期期中数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,图形中的度数为(
)
A.
B.
C.
D.
2.如图,小手盖住的点的坐标可能为(
)
A.
B.
C.
D.
3.如图,在□ABCD中,对角线AC,BD相交于点O,E是BC的中点,若OE=3,则AB的长为(
)
A.3
B.6
C.9
D.12
4.如图,菱形中,,则(
)
A.
B.
C.
D.
5.一个多边形的内角和是外角和的3倍,则这个多边形是(
)
A.六边形
B.七边形
C.八边形
D.九边形
6.已知,OC为一射线,OM,ON分别平分∠BOC和∠AOC,则∠MON是(
)
A.
B.
C.或
D.或
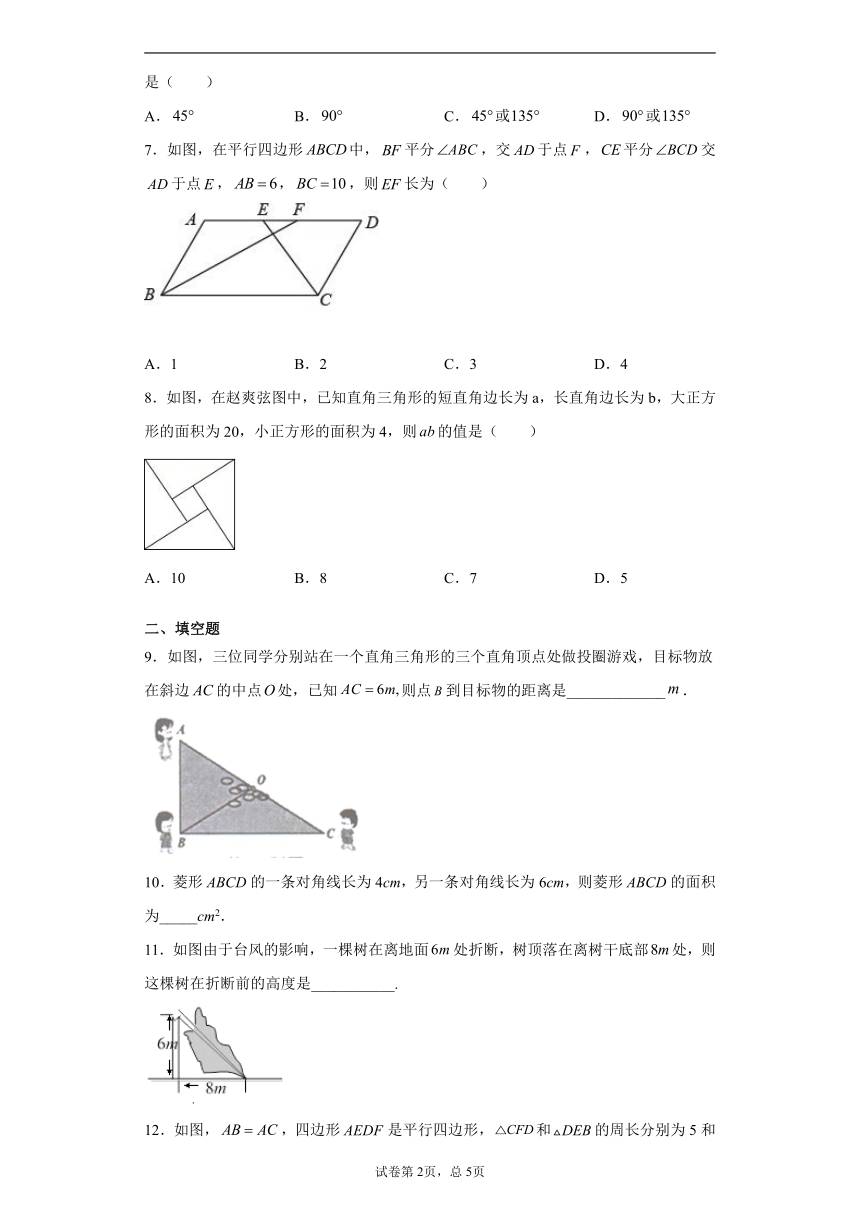
7.如图,在平行四边形中,平分,交于点,平分交于点,,,则长为(
)
A.1
B.2
C.3
D.4
8.如图,在赵爽弦图中,已知直角三角形的短直角边长为a,长直角边长为b,大正方形的面积为20,小正方形的面积为4,则的值是( )
A.10
B.8
C.7
D.5
二、填空题
9.如图,三位同学分别站在一个直角三角形的三个直角顶点处做投圈游戏,目标物放在斜边的中点处,已知则点到目标物的距离是_____________.
10.菱形ABCD的一条对角线长为4cm,另一条对角线长为6cm,则菱形ABCD的面积为_____cm2.
11.如图由于台风的影响,一棵树在离地面处折断,树顶落在离树干底部处,则这棵树在折断前的高度是___________.
12.如图,,四边形是平行四边形,和的周长分别为5和10,则的周长是_______.
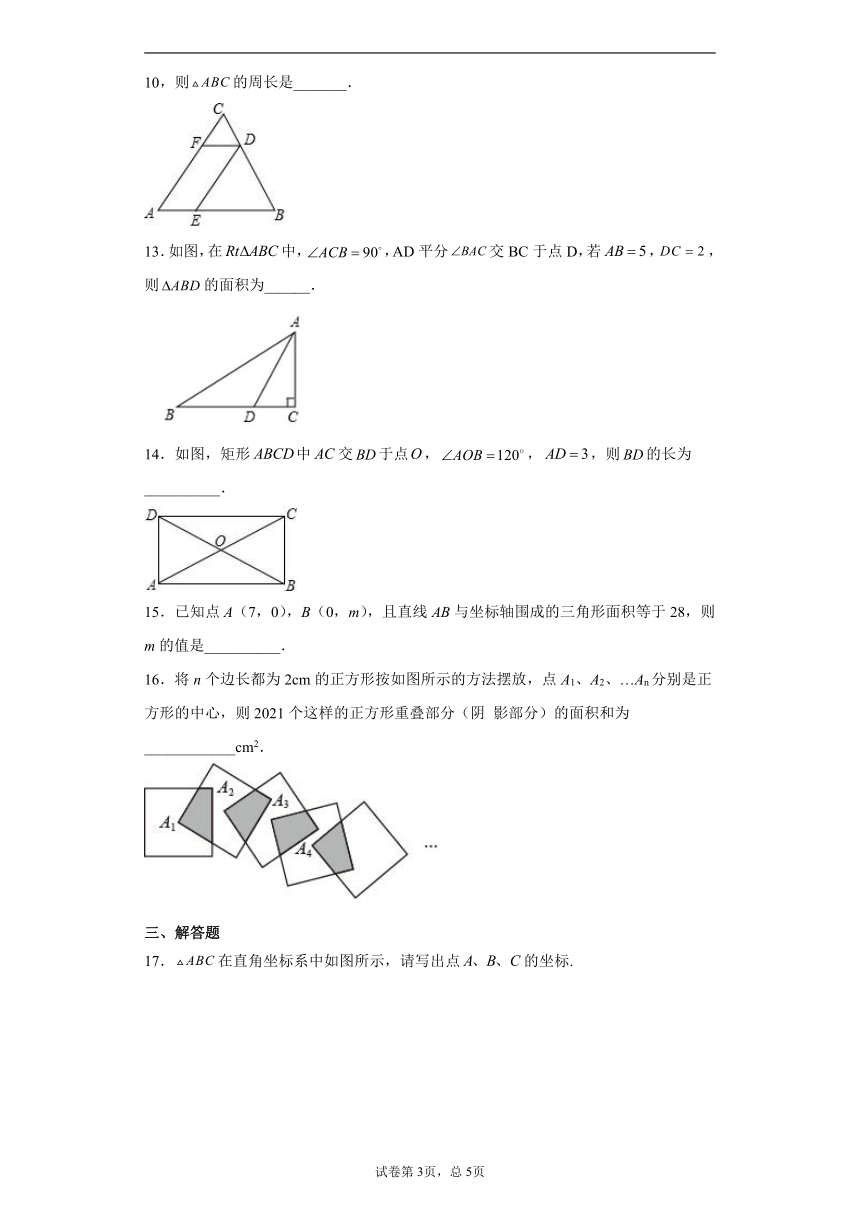
13.如图,在中,,AD平分交BC于点D,若,,则的面积为______.
14.如图,矩形中交于点,,,则的长为__________.
15.已知点A(7,0),B(0,m),且直线AB与坐标轴围成的三角形面积等于28,则m的值是__________.
16.将n个边长都为2cm的正方形按如图所示的方法摆放,点A1、A2、…An分别是正方形的中心,则2021个这样的正方形重叠部分(阴
影部分)的面积和为____________cm2.
三、解答题
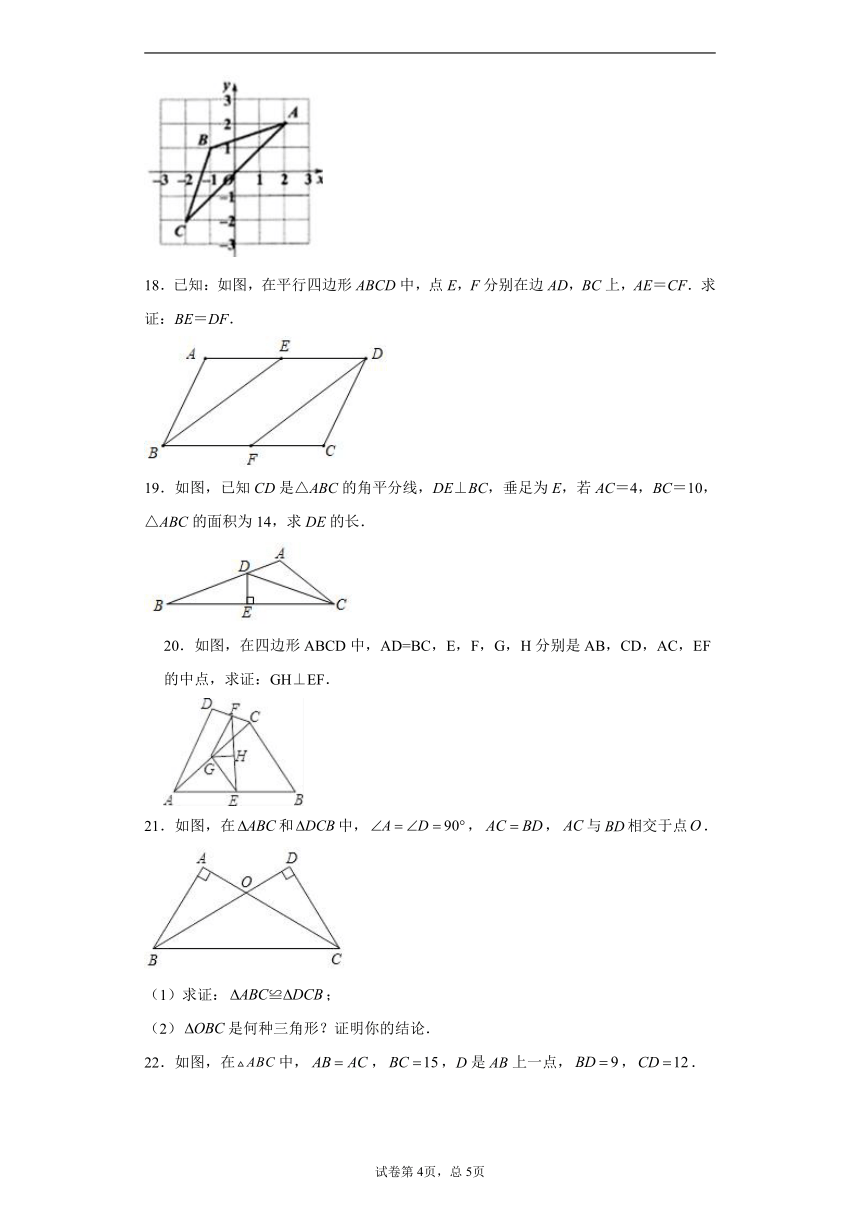
17.在直角坐标系中如图所示,请写出点的坐标.
18.已知:如图,在平行四边形ABCD中,点E,F分别在边AD,BC上,AE=CF.求证:BE=DF.
19.如图,已知CD是△ABC的角平分线,DE⊥BC,垂足为E,若AC=4,BC=10,△ABC的面积为14,求DE的长.
20.如图,在四边形ABCD中,AD=BC,E,F,G,H分别是AB,CD,AC,EF的中点,求证:GH⊥EF.
21.如图,在和中,,,与相交于点.
(1)求证:;
(2)是何种三角形?证明你的结论.
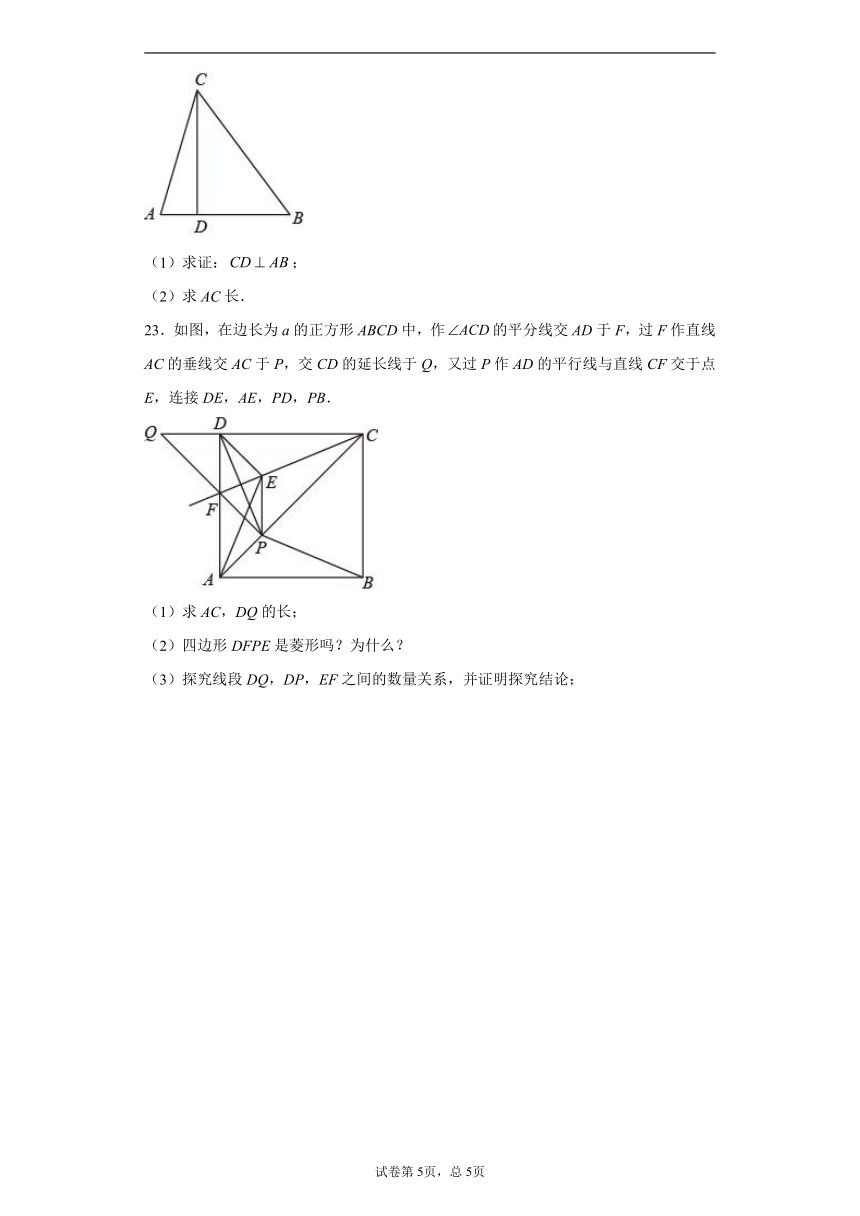
22.如图,在中,,,D是AB上一点,,.
(1)求证:;
(2)求AC长.
23.如图,在边长为a的正方形ABCD中,作的平分线交AD于F,过F作直线AC的垂线交AC于P,交CD的延长线于Q,又过P作AD的平行线与直线CF交于点E,连接DE,AE,PD,PB.
(1)求AC,DQ的长;
(2)四边形DFPE是菱形吗?为什么?
(3)探究线段DQ,DP,EF之间的数量关系,并证明探究结论;
试卷第1页,总3页
试卷第1页,总3页
参考答案
1.D
【分析】
由三角形内角和定理:三角形的三个内角的和为180°求解即可得到答案.
【详解】
解:由题意可知,∠1+40°+90°=180°
∴∠1=180°-40°-90°=50°
故选D.
【点睛】
本题主要考查了三角形的内角和定理,解题的关键在于能够熟练掌握三角形的内角和定理.
2.C
【分析】
根据各象限内点的坐标特征解答即可.
【详解】
解:由图可知:
小手盖住的部分在第四象限,
故符合要求的点为(3,-3),
故选:C.
【点睛】
本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
3.B
【分析】
点O是AC的中点,E是BC的中点,则OE是三角形ABC的中位线,据此计算即可
【详解】
∵在□ABCD中,对角线AC,BD相交于点O,
∴OA=OC,
∵EB=EC,
∴AB=2OE,
∵OE=3,
∴AB=6,
故选:B.
【点睛】
本题考查了平行四边形的性质,三角形的中位线定理,熟练掌握平行四边形的性质,灵活运用三角形中位线定理是解题的关键.
4.B
【分析】
直接利用菱形的性质得出,,进而结合平行四边形的性质得出答案.
【详解】
解:四边形是菱形,
,,
,
,
.
故选:B.
【点睛】
此题主要考查了菱形的性质,正确得出的度数是解题关键.
5.C
【详解】
解:设多边形的边数是n,根据题意得,
(n﹣2)?180°=3×360°,
解得n=8,
∴这个多边形为八边形.
故选C.
【点评】本题主要考查了多边形的内角和公式与外角和定理,根据题意列出方程是解题的关键,要注意“八”不能用阿拉伯数字写.
6.C
【分析】
分射线OC在∠AOB内部和外部两种情况,讨论求解即可得到答案.
【详解】
解:当射线OC在∠AOB内部时,如图所示
∵OM,ON分别平分∠BOC和∠AOC
∴∠AON=∠NOC,∠COM=∠BOM
又∵∠AOB=90°
∴2(∠NOC+∠COM)=90°
∴∠MON=∠NOC+∠COM=45°
当射线OC在∠AOB外部时,∠COB为锐角时
∵OM,ON分别平分∠BOC和∠AOC
∴∠AON=∠NOC,∠COM=∠BOM
又∵∠AOB=90°
∴∠AON+∠NOB=90°
∴∠NOB+∠BOM+∠MOC+∠NOB
=90°
∴∠NOB+∠BOM=45°
∴∠MON=45°
当射线OC在∠AOB外部时,∠COB为直角时
此时ON与OB重合,
∵OM,ON分别平分∠BOC和∠AOC
∴∠MON=45°
当射线OC在∠AOB外部时,∠COB为钝角时
∵∵OM,ON分别平分∠BOC和∠AOC
∴∠AON=∠NOC,∠COM=∠BOM
又∵∠AOB=90°
∴∠AOC+∠BOC=360°-90°=270°
∴∠AON+∠NOC+∠COM+∠BOM=270°
∴∠NOC+∠COM=135°
∴∠MON=135°
当射线OC在∠AOB外部时,∠COB为平角时
同理可以求得∠MON=135°
综上所述,∠MON=45°或∠MON=135°
故选C.
【点睛】
本题主要考查了角平分线的定义,解题的关键在于能够熟练掌握角平分线的定义.
7.B
【分析】
根据平行四边形的性质可得,由角平分线可得,所以,所以,同理可得,则根据即可求解.
【详解】
∵四边形是平行四边形,
∴AD∥BC,,,
∴,
∵平分,
∴,
∴,
∴,
同理可得,
∴.
故选:B.
【点睛】
本题主要考查了平行四边形的性质,等腰三角形的判定与性质,角平分线的定义,解题的关键是依据数学模型“角平分线+平行线等腰三角形”转化线段.
8.B
【分析】
设大正方形的边长为c,则c2=20,小正方形的面积(a?b)2=4,再由勾股定理a2+b2=c2,从而可得出ab的值.
【详解】
解:设大正方形的边长为c,则c2=20,小正方形的面积(a?b)2=4,
∵a2+b2=c2=20,(a?b)2=4,
∴a2+b2?2ab=4,即20?2ab=4.
∴ab=8.
故选:B.
【点睛】
本题考查了勾股定理的运用,要注意的是本题中求不出两直角边的值,注意完全平方公式的灵活运用,有一定难度.
9.3
【分析】
根据直角三角形斜边上的中线等于斜边的一半可得;
【详解】
由题可得△ABC是直角三角形,BO是斜边上的中线,根据直角三角形斜边上的中线等于斜边的一半可知:AO=CO=BO,
∵,
∴,
∴点到目标物的距离是,
故答案是.
【点睛】
本题主要考查了直角三角形斜边上的中线等于斜边的一半,准确理解计算是解题的关键.
10.12
【分析】
根据菱形的面积等于两对角线乘积的一半求得菱形的面积.
【详解】
解:∵菱形ABCD的一条对角线长为4cm,另一条对角线长为6cm,
∴菱形ABCD的面积为6×4=12(cm2).
故答案为:12.
【点睛】
本题主要考查菱形的面积公式的运用,菱形的面积等于两条对角线的积的一半.
11.16米.
【分析】
根据大树折断部分、下部、地面恰好构成直角三角形,根据勾股定理解答即可.
【详解】
由题意得BC=8m,AB=6m,
在直角三角形ABC中,根据勾股定理得:AC==10(米).
所以大树的高度是10+6=16(米).
故答案为16米.
【点睛】
此题考查勾股定理的应用,解题关键在于利用勾股定理进行计算.
12.15
【分析】
根据平行四边形的对边相等可得DE=AF,DF=AE,再根据三角形周长的定义结合已知条件即可求出△ABC的周长.
【详解】
解:∵四边形AEDF是平行四边形,
∴DE=AF,DF=AE,
∵△CFD和△DEB的周长分别为5和10,
∴CF+DF+CD=5,DE+EB+DB=10,
∴CF+AE+CD=5,AF+EB+DB=10,
∴△ABC的周长=CF+AF+AE+EB+BD+CD=15.
故答案为:15.
【点睛】
此题主要考查了平行四边形的性质,掌握平行四边形的对边相等是解题的关键.
13.5
【分析】
作DH⊥AB于H,如图,根据角平分线的性质得到DH=DC=2,然后根据三角形面积公式计算.
【详解】
解:作DH⊥AB于H,如图,
∵AD平分∠BAC,DH⊥AB,DC⊥AC,
∴DH=DC=2,
∴△ABD的面积=
故答案为5.
【点睛】
本题考查了角平分线的性质:角的平分线上的点到角的两边的距离相等.
14.6
【分析】
根据矩形的对角线相等且互相平分可得OA=OD,再求出∠AOD=60°,然后判断出△AOD是等边三角形,根据等边三角形的性质求出OD,即可得出BD的长.
【详解】
解:在矩形ABCD中,OA=OC=AC,OB=OD=BD,AC=BD,
∴OA=OD,
∵∠AOB=120°,
∴∠AOD=180°-120°=60°,
∴△AOD是等边三角形,
∴OD=AD=3,
∴BD=2OD=6;
故答案为:6.
【点睛】
本题考查了矩形的性质,等边三角形的判定与性质,熟记矩形的性质,证出△AOD是等边三角形是解题的关键.
15.
【分析】
先分别求出点A、点B到坐标轴的距离即OA、OB,再利用三角形的面积公式求解即可.
【详解】
解:∵点A(7,0),B(0,m),
∴OA=7,OB=|m|,
∵直线AB与坐标轴围成的三角形面积等于28,
∴×7×|m|=28,
解得:m=±8,
故答案为:±8.
【点睛】
本题考查了坐标与图形性质、三角形的面积公式,熟练掌握坐标与图形的性质,会利用点的坐标求图形的面积的方法是解答的关键.
16.2020
【分析】
根据题意可得,阴影部分的面积是正方形的面积的,已知两个正方形可得到一个阴影部分,则n个这样的正方形重叠部分即为(n-1)阴影部分的和.
【详解】
解:作A1E⊥A2E,A1F⊥A2H.
则∠FA1E=∠HA1G=90°,
∵∠FA1H+∠HA1E=90°,∠FA1G+∠HA1E=90°
∴∠FA1H=∠GA1E,
在△A1HF和△A1GE中,
,
∴△A1HF≌△A1GE,
∵A1是正方形的中心,正方形的边长为2cm
∴四边形A2HA1G的面积=四边形A1EA2F的面积=×4=1,
同理,各个重合部分的面积都是1(cm2),
则n个这样的正方形重叠部分(阴影部分)的面积和为1×(n-1)=n-1(cm2),
∴2021个这样的正方形重叠部分(阴影部分)的面积和为:2021-1=2020(cm2),
故答案为:2020.
【点睛】
本题考查了正方形的性质,解决本题的关键是得到n个这样的正方形重叠部分(阴影部分)的面积和的计算方法,难点是求得一个阴影部分的面积.
17..
【分析】
根据平面直角坐标系的特点写出点A、B、C的坐标;
【详解】
解:由平面直角坐标系可得:A(2,2),B(-1,1),C(-2,-2);
故答案为A(2,2),B(-1,1),C(-2,-2).
【点睛】
本题考查了平面直角坐标系点的坐标,解题的关键是熟练掌握基本知识.
18.见解析
【分析】
先求出DE=BF,再证明四边形BEDF是平行四边形,即可得出结论.
【详解】
解:证明:∵四边形ABCD是平行四边形
∴AD=BC,AD∥BC,
∵AE=CF,
∴DE=BF,
又∵DE∥BF,
∴四边形BEDF是平行四边形,
∴BE=DF.
【点睛】
本题考查了平行四边形的判定与性质;熟练掌握平行四边形的判定方法,证明四边形是平行四边形是解决问题的关键.
19.DE=2
【分析】
过点D作DF⊥AC交CA的延长线于点F,如图,利用角平分线的性质得到DF=DE.再利用三角形面积公式得到×DE×10+×DF×4=14,然后解方程即可.
【详解】
解:过点D作DF⊥AC交CA的延长线于点F,如图,
∵CD平分∠ACB,DE⊥BC于E,
∴DF=DE.
∵△ABC的面积为14,
∴S△BCD+S△ACD=14,
∴×DE×10+×DF×4=14,
即5DE+2DE=14,
∴DE=2.
【点睛】
本题考查了角平分线的性质:角的平分线上的点到角的两边的距离相等;掌握知识点是解题关键.
20.见解析
【分析】
根据三角形中位线的性质得到FG=AD,EG=BC,由AD=BC,于是得到FG=GE,根据等腰三角形的性质即可得到结论.
【详解】
证明:∵E,F,G分别是AB,CD,AC的中点,
∴FG=AD,EG=BC,
∵AD=BC,
∴FG=GE,
∵H是EF的中点,
∴GH⊥EF.
【点睛】
本题考查了三角形的中位线的性质,等腰三角形的判定和性质,少了掌握三角形的中位线的性质是解题的关键.
21.(1)见解析;(2)是等腰三角形,证明见解析
【分析】
(1)根据已知条件,用HL直接证明Rt△ABC≌Rt△DCB即可;
(2)利用全等三角形的对应角相等得到∠ACB=∠DBC,即可证明△OBC是等腰三角形.
【详解】
证明:(1)在和中,
,为公共边,
∴
(2)是等腰三角形
∵
∴
∴
∴是等腰三角形
【点睛】
此题主要考查学生对直角三角形全等的判定和性质以及等腰三角形的判定的理解和掌握,熟练掌握相关判定定理和性质定理是解题关键.
22.(1)见解析;(2)
【分析】
(1)根据勾股定理的逆定理即可得到结论;
(2)根据勾股定理列方程即可得到结论.
【详解】
解:(1)证明:,,,
,
,
;
(2)解:,
,
,
,
,
,
.
【点睛】
本题考查了勾股定理的逆定理,勾股定理,正确的识别图形是解题的关键.
23.(1),;(2)是,理由见解析;(3),证明见解析
【分析】
(1)利用勾股定理求出对角线AC,再证明,得出QD=AP,再证明,得出CD=CP即可求出结果;
(2)先证明FC是线段DP的垂直平分线,得出DE=EP,根据等腰三角形的性质得出,,由已知EP∥DF,证明出DE∥PF,结合EP∥DF,得出四边形DFPE是平行四边形,再由EF⊥DP,判定出菱形;
(3)设DP与EF交于点G,根据菱形的性质得到,,再证明为等腰直角三角形,得出QD=DF,最后在中,由勾股定理证明出线段关系.
【详解】
解:(1),
∵CF平分,,,
,
又∵,四边形ABCD为正方形,
∴,
在和中
∵
,
,
在和中,
∵
∴,
,
;
(2)是菱形,证明如下:
,
∴CF垂直平分DP,即,
,则,
,
,
又∵EP∥DF,
,
,
,
∥,而EP∥DF,
∴四边形DFPE是平行四边形,
,
∴四边形DFPE是菱形;
(3),理由如下:
∵四边形DFPE是菱形,设DP与EF交于点G,如图,
由(2)得,,,,
∵四边形ABCD为正方形,
∴,
又∵,
∴为等腰直角三角形,
,
∴为等腰直角三角形,
,
在中,
∵,
∴有,整理得:.
【点睛】
本题考查了正方形的性质,等腰直角三角形的判定与性质,全等三角形的判定与性质,菱形的判定与性质,勾股定理,解题关键是熟练掌握相关知识点,同时注意各个小问之间的关系.
答案第1页,总2页
答案第1页,总2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,图形中的度数为(
)
A.
B.
C.
D.
2.如图,小手盖住的点的坐标可能为(
)
A.
B.
C.
D.
3.如图,在□ABCD中,对角线AC,BD相交于点O,E是BC的中点,若OE=3,则AB的长为(
)
A.3
B.6
C.9
D.12
4.如图,菱形中,,则(
)
A.
B.
C.
D.
5.一个多边形的内角和是外角和的3倍,则这个多边形是(
)
A.六边形
B.七边形
C.八边形
D.九边形
6.已知,OC为一射线,OM,ON分别平分∠BOC和∠AOC,则∠MON是(
)
A.
B.
C.或
D.或
7.如图,在平行四边形中,平分,交于点,平分交于点,,,则长为(
)
A.1
B.2
C.3
D.4
8.如图,在赵爽弦图中,已知直角三角形的短直角边长为a,长直角边长为b,大正方形的面积为20,小正方形的面积为4,则的值是( )
A.10
B.8
C.7
D.5
二、填空题
9.如图,三位同学分别站在一个直角三角形的三个直角顶点处做投圈游戏,目标物放在斜边的中点处,已知则点到目标物的距离是_____________.
10.菱形ABCD的一条对角线长为4cm,另一条对角线长为6cm,则菱形ABCD的面积为_____cm2.
11.如图由于台风的影响,一棵树在离地面处折断,树顶落在离树干底部处,则这棵树在折断前的高度是___________.
12.如图,,四边形是平行四边形,和的周长分别为5和10,则的周长是_______.
13.如图,在中,,AD平分交BC于点D,若,,则的面积为______.
14.如图,矩形中交于点,,,则的长为__________.
15.已知点A(7,0),B(0,m),且直线AB与坐标轴围成的三角形面积等于28,则m的值是__________.
16.将n个边长都为2cm的正方形按如图所示的方法摆放,点A1、A2、…An分别是正方形的中心,则2021个这样的正方形重叠部分(阴
影部分)的面积和为____________cm2.
三、解答题
17.在直角坐标系中如图所示,请写出点的坐标.
18.已知:如图,在平行四边形ABCD中,点E,F分别在边AD,BC上,AE=CF.求证:BE=DF.
19.如图,已知CD是△ABC的角平分线,DE⊥BC,垂足为E,若AC=4,BC=10,△ABC的面积为14,求DE的长.
20.如图,在四边形ABCD中,AD=BC,E,F,G,H分别是AB,CD,AC,EF的中点,求证:GH⊥EF.
21.如图,在和中,,,与相交于点.
(1)求证:;
(2)是何种三角形?证明你的结论.
22.如图,在中,,,D是AB上一点,,.
(1)求证:;
(2)求AC长.
23.如图,在边长为a的正方形ABCD中,作的平分线交AD于F,过F作直线AC的垂线交AC于P,交CD的延长线于Q,又过P作AD的平行线与直线CF交于点E,连接DE,AE,PD,PB.
(1)求AC,DQ的长;
(2)四边形DFPE是菱形吗?为什么?
(3)探究线段DQ,DP,EF之间的数量关系,并证明探究结论;
试卷第1页,总3页
试卷第1页,总3页
参考答案
1.D
【分析】
由三角形内角和定理:三角形的三个内角的和为180°求解即可得到答案.
【详解】
解:由题意可知,∠1+40°+90°=180°
∴∠1=180°-40°-90°=50°
故选D.
【点睛】
本题主要考查了三角形的内角和定理,解题的关键在于能够熟练掌握三角形的内角和定理.
2.C
【分析】
根据各象限内点的坐标特征解答即可.
【详解】
解:由图可知:
小手盖住的部分在第四象限,
故符合要求的点为(3,-3),
故选:C.
【点睛】
本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
3.B
【分析】
点O是AC的中点,E是BC的中点,则OE是三角形ABC的中位线,据此计算即可
【详解】
∵在□ABCD中,对角线AC,BD相交于点O,
∴OA=OC,
∵EB=EC,
∴AB=2OE,
∵OE=3,
∴AB=6,
故选:B.
【点睛】
本题考查了平行四边形的性质,三角形的中位线定理,熟练掌握平行四边形的性质,灵活运用三角形中位线定理是解题的关键.
4.B
【分析】
直接利用菱形的性质得出,,进而结合平行四边形的性质得出答案.
【详解】
解:四边形是菱形,
,,
,
,
.
故选:B.
【点睛】
此题主要考查了菱形的性质,正确得出的度数是解题关键.
5.C
【详解】
解:设多边形的边数是n,根据题意得,
(n﹣2)?180°=3×360°,
解得n=8,
∴这个多边形为八边形.
故选C.
【点评】本题主要考查了多边形的内角和公式与外角和定理,根据题意列出方程是解题的关键,要注意“八”不能用阿拉伯数字写.
6.C
【分析】
分射线OC在∠AOB内部和外部两种情况,讨论求解即可得到答案.
【详解】
解:当射线OC在∠AOB内部时,如图所示
∵OM,ON分别平分∠BOC和∠AOC
∴∠AON=∠NOC,∠COM=∠BOM
又∵∠AOB=90°
∴2(∠NOC+∠COM)=90°
∴∠MON=∠NOC+∠COM=45°
当射线OC在∠AOB外部时,∠COB为锐角时
∵OM,ON分别平分∠BOC和∠AOC
∴∠AON=∠NOC,∠COM=∠BOM
又∵∠AOB=90°
∴∠AON+∠NOB=90°
∴∠NOB+∠BOM+∠MOC+∠NOB
=90°
∴∠NOB+∠BOM=45°
∴∠MON=45°
当射线OC在∠AOB外部时,∠COB为直角时
此时ON与OB重合,
∵OM,ON分别平分∠BOC和∠AOC
∴∠MON=45°
当射线OC在∠AOB外部时,∠COB为钝角时
∵∵OM,ON分别平分∠BOC和∠AOC
∴∠AON=∠NOC,∠COM=∠BOM
又∵∠AOB=90°
∴∠AOC+∠BOC=360°-90°=270°
∴∠AON+∠NOC+∠COM+∠BOM=270°
∴∠NOC+∠COM=135°
∴∠MON=135°
当射线OC在∠AOB外部时,∠COB为平角时
同理可以求得∠MON=135°
综上所述,∠MON=45°或∠MON=135°
故选C.
【点睛】
本题主要考查了角平分线的定义,解题的关键在于能够熟练掌握角平分线的定义.
7.B
【分析】
根据平行四边形的性质可得,由角平分线可得,所以,所以,同理可得,则根据即可求解.
【详解】
∵四边形是平行四边形,
∴AD∥BC,,,
∴,
∵平分,
∴,
∴,
∴,
同理可得,
∴.
故选:B.
【点睛】
本题主要考查了平行四边形的性质,等腰三角形的判定与性质,角平分线的定义,解题的关键是依据数学模型“角平分线+平行线等腰三角形”转化线段.
8.B
【分析】
设大正方形的边长为c,则c2=20,小正方形的面积(a?b)2=4,再由勾股定理a2+b2=c2,从而可得出ab的值.
【详解】
解:设大正方形的边长为c,则c2=20,小正方形的面积(a?b)2=4,
∵a2+b2=c2=20,(a?b)2=4,
∴a2+b2?2ab=4,即20?2ab=4.
∴ab=8.
故选:B.
【点睛】
本题考查了勾股定理的运用,要注意的是本题中求不出两直角边的值,注意完全平方公式的灵活运用,有一定难度.
9.3
【分析】
根据直角三角形斜边上的中线等于斜边的一半可得;
【详解】
由题可得△ABC是直角三角形,BO是斜边上的中线,根据直角三角形斜边上的中线等于斜边的一半可知:AO=CO=BO,
∵,
∴,
∴点到目标物的距离是,
故答案是.
【点睛】
本题主要考查了直角三角形斜边上的中线等于斜边的一半,准确理解计算是解题的关键.
10.12
【分析】
根据菱形的面积等于两对角线乘积的一半求得菱形的面积.
【详解】
解:∵菱形ABCD的一条对角线长为4cm,另一条对角线长为6cm,
∴菱形ABCD的面积为6×4=12(cm2).
故答案为:12.
【点睛】
本题主要考查菱形的面积公式的运用,菱形的面积等于两条对角线的积的一半.
11.16米.
【分析】
根据大树折断部分、下部、地面恰好构成直角三角形,根据勾股定理解答即可.
【详解】
由题意得BC=8m,AB=6m,
在直角三角形ABC中,根据勾股定理得:AC==10(米).
所以大树的高度是10+6=16(米).
故答案为16米.
【点睛】
此题考查勾股定理的应用,解题关键在于利用勾股定理进行计算.
12.15
【分析】
根据平行四边形的对边相等可得DE=AF,DF=AE,再根据三角形周长的定义结合已知条件即可求出△ABC的周长.
【详解】
解:∵四边形AEDF是平行四边形,
∴DE=AF,DF=AE,
∵△CFD和△DEB的周长分别为5和10,
∴CF+DF+CD=5,DE+EB+DB=10,
∴CF+AE+CD=5,AF+EB+DB=10,
∴△ABC的周长=CF+AF+AE+EB+BD+CD=15.
故答案为:15.
【点睛】
此题主要考查了平行四边形的性质,掌握平行四边形的对边相等是解题的关键.
13.5
【分析】
作DH⊥AB于H,如图,根据角平分线的性质得到DH=DC=2,然后根据三角形面积公式计算.
【详解】
解:作DH⊥AB于H,如图,
∵AD平分∠BAC,DH⊥AB,DC⊥AC,
∴DH=DC=2,
∴△ABD的面积=
故答案为5.
【点睛】
本题考查了角平分线的性质:角的平分线上的点到角的两边的距离相等.
14.6
【分析】
根据矩形的对角线相等且互相平分可得OA=OD,再求出∠AOD=60°,然后判断出△AOD是等边三角形,根据等边三角形的性质求出OD,即可得出BD的长.
【详解】
解:在矩形ABCD中,OA=OC=AC,OB=OD=BD,AC=BD,
∴OA=OD,
∵∠AOB=120°,
∴∠AOD=180°-120°=60°,
∴△AOD是等边三角形,
∴OD=AD=3,
∴BD=2OD=6;
故答案为:6.
【点睛】
本题考查了矩形的性质,等边三角形的判定与性质,熟记矩形的性质,证出△AOD是等边三角形是解题的关键.
15.
【分析】
先分别求出点A、点B到坐标轴的距离即OA、OB,再利用三角形的面积公式求解即可.
【详解】
解:∵点A(7,0),B(0,m),
∴OA=7,OB=|m|,
∵直线AB与坐标轴围成的三角形面积等于28,
∴×7×|m|=28,
解得:m=±8,
故答案为:±8.
【点睛】
本题考查了坐标与图形性质、三角形的面积公式,熟练掌握坐标与图形的性质,会利用点的坐标求图形的面积的方法是解答的关键.
16.2020
【分析】
根据题意可得,阴影部分的面积是正方形的面积的,已知两个正方形可得到一个阴影部分,则n个这样的正方形重叠部分即为(n-1)阴影部分的和.
【详解】
解:作A1E⊥A2E,A1F⊥A2H.
则∠FA1E=∠HA1G=90°,
∵∠FA1H+∠HA1E=90°,∠FA1G+∠HA1E=90°
∴∠FA1H=∠GA1E,
在△A1HF和△A1GE中,
,
∴△A1HF≌△A1GE,
∵A1是正方形的中心,正方形的边长为2cm
∴四边形A2HA1G的面积=四边形A1EA2F的面积=×4=1,
同理,各个重合部分的面积都是1(cm2),
则n个这样的正方形重叠部分(阴影部分)的面积和为1×(n-1)=n-1(cm2),
∴2021个这样的正方形重叠部分(阴影部分)的面积和为:2021-1=2020(cm2),
故答案为:2020.
【点睛】
本题考查了正方形的性质,解决本题的关键是得到n个这样的正方形重叠部分(阴影部分)的面积和的计算方法,难点是求得一个阴影部分的面积.
17..
【分析】
根据平面直角坐标系的特点写出点A、B、C的坐标;
【详解】
解:由平面直角坐标系可得:A(2,2),B(-1,1),C(-2,-2);
故答案为A(2,2),B(-1,1),C(-2,-2).
【点睛】
本题考查了平面直角坐标系点的坐标,解题的关键是熟练掌握基本知识.
18.见解析
【分析】
先求出DE=BF,再证明四边形BEDF是平行四边形,即可得出结论.
【详解】
解:证明:∵四边形ABCD是平行四边形
∴AD=BC,AD∥BC,
∵AE=CF,
∴DE=BF,
又∵DE∥BF,
∴四边形BEDF是平行四边形,
∴BE=DF.
【点睛】
本题考查了平行四边形的判定与性质;熟练掌握平行四边形的判定方法,证明四边形是平行四边形是解决问题的关键.
19.DE=2
【分析】
过点D作DF⊥AC交CA的延长线于点F,如图,利用角平分线的性质得到DF=DE.再利用三角形面积公式得到×DE×10+×DF×4=14,然后解方程即可.
【详解】
解:过点D作DF⊥AC交CA的延长线于点F,如图,
∵CD平分∠ACB,DE⊥BC于E,
∴DF=DE.
∵△ABC的面积为14,
∴S△BCD+S△ACD=14,
∴×DE×10+×DF×4=14,
即5DE+2DE=14,
∴DE=2.
【点睛】
本题考查了角平分线的性质:角的平分线上的点到角的两边的距离相等;掌握知识点是解题关键.
20.见解析
【分析】
根据三角形中位线的性质得到FG=AD,EG=BC,由AD=BC,于是得到FG=GE,根据等腰三角形的性质即可得到结论.
【详解】
证明:∵E,F,G分别是AB,CD,AC的中点,
∴FG=AD,EG=BC,
∵AD=BC,
∴FG=GE,
∵H是EF的中点,
∴GH⊥EF.
【点睛】
本题考查了三角形的中位线的性质,等腰三角形的判定和性质,少了掌握三角形的中位线的性质是解题的关键.
21.(1)见解析;(2)是等腰三角形,证明见解析
【分析】
(1)根据已知条件,用HL直接证明Rt△ABC≌Rt△DCB即可;
(2)利用全等三角形的对应角相等得到∠ACB=∠DBC,即可证明△OBC是等腰三角形.
【详解】
证明:(1)在和中,
,为公共边,
∴
(2)是等腰三角形
∵
∴
∴
∴是等腰三角形
【点睛】
此题主要考查学生对直角三角形全等的判定和性质以及等腰三角形的判定的理解和掌握,熟练掌握相关判定定理和性质定理是解题关键.
22.(1)见解析;(2)
【分析】
(1)根据勾股定理的逆定理即可得到结论;
(2)根据勾股定理列方程即可得到结论.
【详解】
解:(1)证明:,,,
,
,
;
(2)解:,
,
,
,
,
,
.
【点睛】
本题考查了勾股定理的逆定理,勾股定理,正确的识别图形是解题的关键.
23.(1),;(2)是,理由见解析;(3),证明见解析
【分析】
(1)利用勾股定理求出对角线AC,再证明,得出QD=AP,再证明,得出CD=CP即可求出结果;
(2)先证明FC是线段DP的垂直平分线,得出DE=EP,根据等腰三角形的性质得出,,由已知EP∥DF,证明出DE∥PF,结合EP∥DF,得出四边形DFPE是平行四边形,再由EF⊥DP,判定出菱形;
(3)设DP与EF交于点G,根据菱形的性质得到,,再证明为等腰直角三角形,得出QD=DF,最后在中,由勾股定理证明出线段关系.
【详解】
解:(1),
∵CF平分,,,
,
又∵,四边形ABCD为正方形,
∴,
在和中
∵
,
,
在和中,
∵
∴,
,
;
(2)是菱形,证明如下:
,
∴CF垂直平分DP,即,
,则,
,
,
又∵EP∥DF,
,
,
,
∥,而EP∥DF,
∴四边形DFPE是平行四边形,
,
∴四边形DFPE是菱形;
(3),理由如下:
∵四边形DFPE是菱形,设DP与EF交于点G,如图,
由(2)得,,,,
∵四边形ABCD为正方形,
∴,
又∵,
∴为等腰直角三角形,
,
∴为等腰直角三角形,
,
在中,
∵,
∴有,整理得:.
【点睛】
本题考查了正方形的性质,等腰直角三角形的判定与性质,全等三角形的判定与性质,菱形的判定与性质,勾股定理,解题关键是熟练掌握相关知识点,同时注意各个小问之间的关系.
答案第1页,总2页
答案第1页,总2页
同课章节目录
