2021-2022学年高二上学期数学人教A版选修1-1第三章3.3.2函数的极值与导数课件(共15张PPT)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版选修1-1第三章3.3.2函数的极值与导数课件(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 838.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-29 14:31:00 | ||
图片预览



文档简介
(共15张PPT)
3.3.2函数的极值与导数
复习回顾:
函数单调性与导数的关系
函数y=f(x)
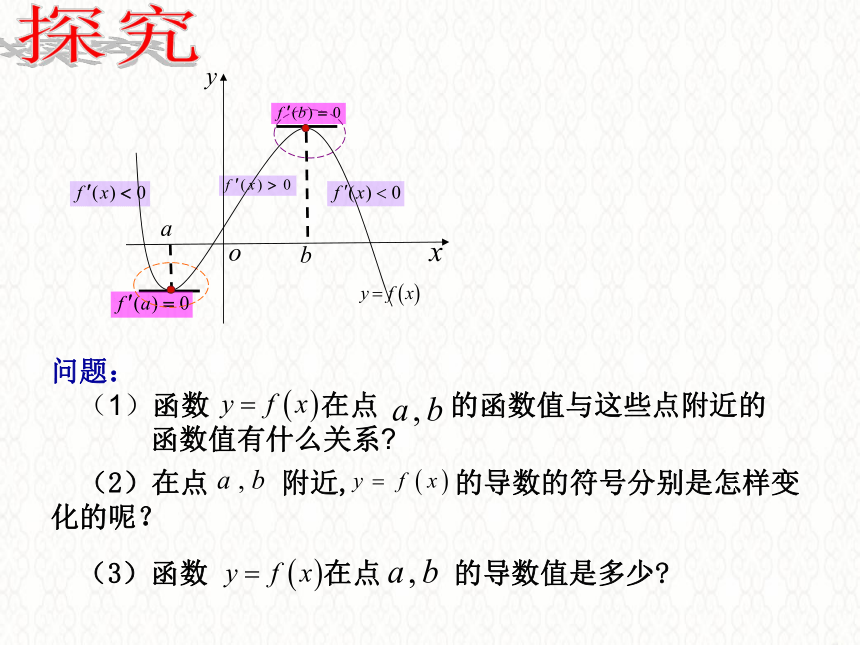
探究
(2)在点
附近,
的导数的符号分别是怎样变化的呢?
(1)函数
在点
的函数值与这些点附近的
函数值有什么关系?
(3)函数
在点
的导数值是多少?
问题:
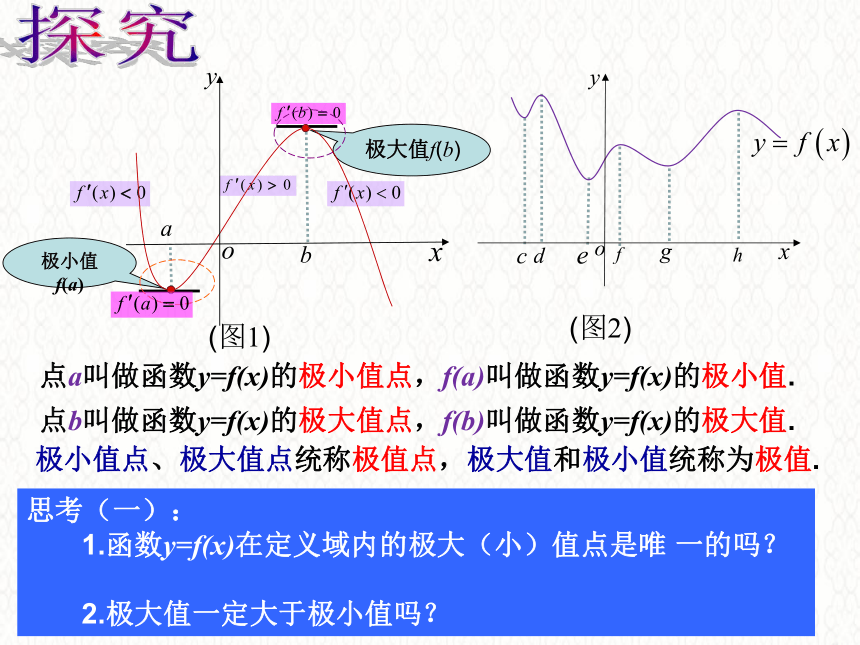
探究
极大值f(b)
点a叫做函数y=f(x)的极小值点,f(a)叫做函数y=f(x)的极小值.
点b叫做函数y=f(x)的极大值点,f(b)叫做函数y=f(x)的极大值.
极小值点、极大值点统称极值点,极大值和极小值统称为极值.
极小值f(a)
思考(一):
1.函数y=f(x)在定义域内的极大(小)值点是唯
一的吗?
2.极大值一定大于极小值吗?
(图2)
(图1)
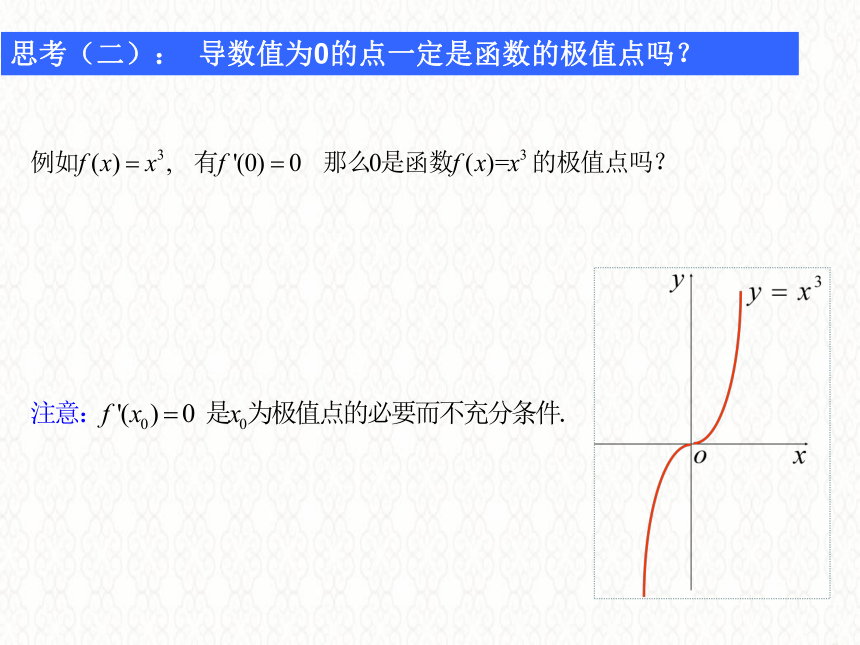
思考(二):
导数值为0的点一定是函数的极值点吗?
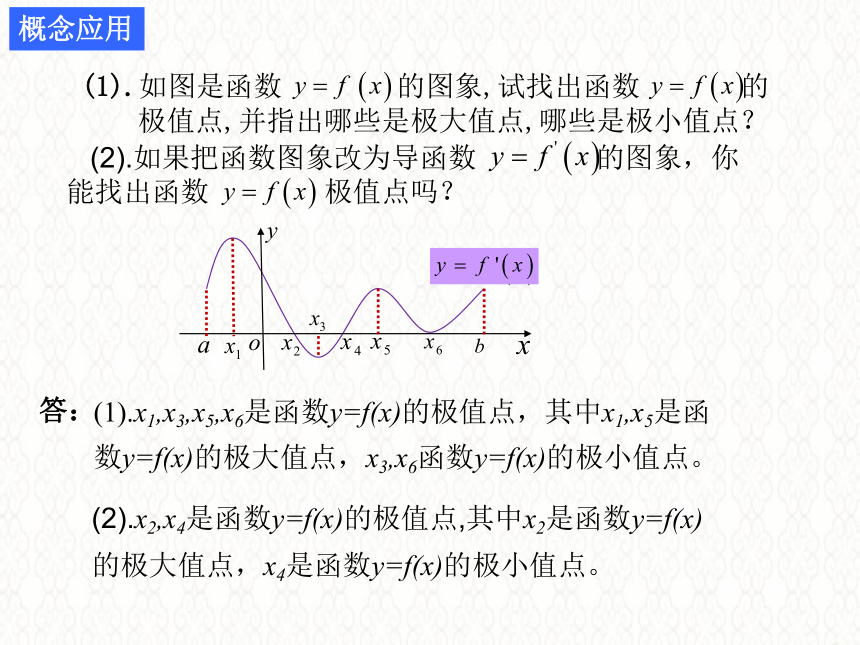
(1).如图是函数
的图象,试找出函数
的
极值点,并指出哪些是极大值点,哪些是极小值点?
(2).如果把函数图象改为导函数
的图象,你能找出函数
极值点吗?
答:
(1).x1,x3,x5,x6是函数y=f(x)的极值点,其中x1,x5是函
数y=f(x)的极大值点,x3,x6函数y=f(x)的极小值点。
(2).x2,x4是函数y=f(x)的极值点,其中x2是函数y=f(x)
的极大值点,x4是函数y=f(x)的极小值点。
概念应用
典例精讲
根据以上计算可以作出该函数的大致图象:
求函数极值(极大值,极小值)的一般方法:
求定义域并求导—解方程—列表—求极值
随堂练习
?
?
?
你能作出该函数的大致图象吗?
?
请作出该函数的大致图象
我的总结,我的收获:
知识层面:
1、极大值、极小值的定义;
2、利用导数求极值的方法;
3、利用极值作函数的大致图象的方法。
方法层面:
数形结合思想;观察、归纳总结思想.
作业:
3.3.2函数的极值与导数
复习回顾:
函数单调性与导数的关系
函数y=f(x)
探究
(2)在点
附近,
的导数的符号分别是怎样变化的呢?
(1)函数
在点
的函数值与这些点附近的
函数值有什么关系?
(3)函数
在点
的导数值是多少?
问题:
探究
极大值f(b)
点a叫做函数y=f(x)的极小值点,f(a)叫做函数y=f(x)的极小值.
点b叫做函数y=f(x)的极大值点,f(b)叫做函数y=f(x)的极大值.
极小值点、极大值点统称极值点,极大值和极小值统称为极值.
极小值f(a)
思考(一):
1.函数y=f(x)在定义域内的极大(小)值点是唯
一的吗?
2.极大值一定大于极小值吗?
(图2)
(图1)
思考(二):
导数值为0的点一定是函数的极值点吗?
(1).如图是函数
的图象,试找出函数
的
极值点,并指出哪些是极大值点,哪些是极小值点?
(2).如果把函数图象改为导函数
的图象,你能找出函数
极值点吗?
答:
(1).x1,x3,x5,x6是函数y=f(x)的极值点,其中x1,x5是函
数y=f(x)的极大值点,x3,x6函数y=f(x)的极小值点。
(2).x2,x4是函数y=f(x)的极值点,其中x2是函数y=f(x)
的极大值点,x4是函数y=f(x)的极小值点。
概念应用
典例精讲
根据以上计算可以作出该函数的大致图象:
求函数极值(极大值,极小值)的一般方法:
求定义域并求导—解方程—列表—求极值
随堂练习
?
?
?
你能作出该函数的大致图象吗?
?
请作出该函数的大致图象
我的总结,我的收获:
知识层面:
1、极大值、极小值的定义;
2、利用导数求极值的方法;
3、利用极值作函数的大致图象的方法。
方法层面:
数形结合思想;观察、归纳总结思想.
作业:
