长方体和正方体的体积(课件) 数学 六年级上册 苏教版(共18张PPT)
文档属性
| 名称 | 长方体和正方体的体积(课件) 数学 六年级上册 苏教版(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-29 09:38:13 | ||
图片预览






文档简介
(共18张PPT)
长方体和正方体的体积
苏教版六年级上
教学目标
在实际操作中,自主探索并掌握长方体和正方体体积公式,能应用公式正确计算长方体和正方体的体积,并能解决一些简单的实际问题。
通过操作、观察、猜想和归纳的探索过程,不断积累立体图形的学习经验,增强空间观念,发展数学思维。
进一步体会数学与生活的联系,获得数学成就感。
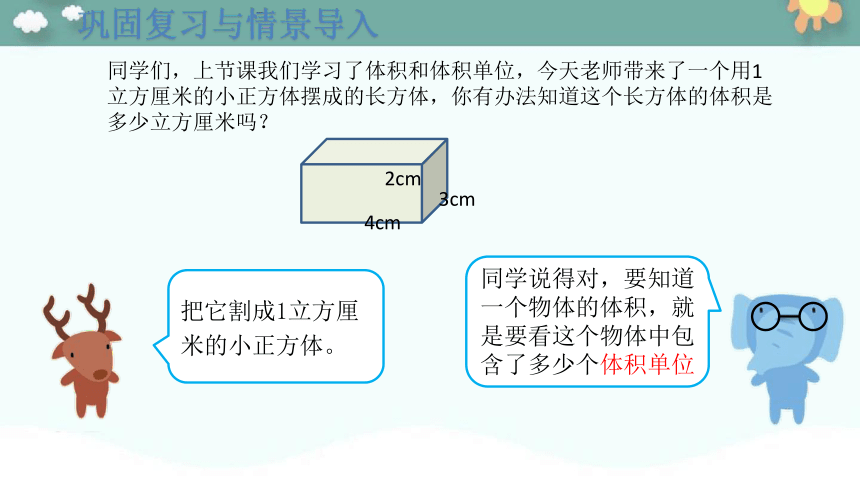
巩固复习与情景导入
把它割成1立方厘米的小正方体。
同学说得对,要知道一个物体的体积,就是要看这个物体中包含了多少个体积单位
4cm
3cm
2cm
同学们,上节课我们学习了体积和体积单位,今天老师带来了一个用1立方厘米的小正方体摆成的长方体,你有办法知道这个长方体的体积是多少立方厘米吗?
把它分割过后如左图,按长方体模型的长、宽、高分割,算出长方体的体积。它有24个体积单位,所以是24立方厘米。
老师的这个长方体模型是用1立方厘米的小正方体摆成的可以分割,但在生活中很多长方体或正方体的物体是不能分割的,如长方体礼盒、文具盒、石块等,它们的体积又有什么办法知道呢?这节课我们一起来研究长方体和正方体的体积计算方法吧。
拿出准备好的长方体,想一想长方体的体积可能与它的什么有关?我们可以用怎样的方法研究长方体的体积?
新授知识
长方体的体积应该与它的长、宽、高有关。
可以把长方体分割成若干个棱长1厘米,1分米或1米的正方体长方体中含有体积单位的个数,算出体积,再和它们的长、宽、高进行比较。
新授知识
同学们说的有道理,方法也不错,但我们需要实验研究才能证明长方体的体积和它的长宽高到底有怎样的关系。
操作探究
操作要求:
1、同桌合作用若干个1立方厘米的正方体,任意摆出四个不同的长方体,并编上序号。
2、观察摆出的长方体的长宽高所用,小正方体的个数,以及它们的体积各是多少?
3、填完表格后,同桌核对数据,并交流自己的发现。
操作探究
长(cm)
宽(cm)
高(cm)
小正方体的个数
体积(cm?)
长方体1
长方体2
长方体3
长方体4
1
2
3
4
3
2
3
18
18
2
2
2
8
8
4
3
2
24
24
2
2
4
16
16
同学们真棒,通过把长方体模型分割的方法,验证了长方体的体积与它长宽高的关系,进而发现了长方体的体积等于它的长宽高的乘积。
我们组摆的是长宽高分别是4,3和2,第一层横着的有4个,竖着的有3个,一共12个,一共有两层,所以是24个,也就是24立方厘米,计算结果和它们的长宽高相乘一致。
长方体的体积=长×宽×高
以后我们可以直接用公式计算长方体的体积,如果用v表示长方体的体积,a、b、h分别表示长方体的长、宽、高,你能用字母表示出长方体的体积公式吗?
长方体的体积=长×宽×高
V=abh
我们都知道正方体是特殊的长方体,想想看正方体的棱长有什么特点?你能直接写出正方体的体积公式吗?
正方体的棱长都相等,所以
正方体的体积=棱长×棱长×棱长
如果正方体的棱长用a表示,你能写出它的公式吗?
V=a?a?a
a?a?a也可以写成a?,读作a的立方,a?表示三个a相乘,正方体的体积公式,一般写成
v=a?
巩固练习
1、计算下面长方体和正方体的体积
10cm
4cm
5cm
2dm
2.2dm
4.5dm
2dm
8cm
8cm
2cm
2.2m
2.2m
2.2m
答:10×5×4=200(cm?)
2×2.2×4.5=19.8(dm?)
8×8×2=128(cm?)
2.2?=10.648(m?)
2、计算
3?=
5?=
10?=
1?=
0.1?=
27
125
1000
1
0.001
3、一种货车的车厢是长方体,从里面量长是5米,宽是1.8米,高是2米,它的容积是多少立方米?
5×1.8×2=18(立方米)
答:它的容积是18立方米。
4、一块正方体木料棱长4分米,这块木料的体积是多少立方分米?如果一立方分米的木料重1.5千克,这块木料重多少千克?
4?=64(立方分米)
64×1.5=96(千克)
答:这块木料的体积是64立方分米,
这块木料重96千克.
本课总结
今天我们一起学习了长方体和正方体体积的计算方法,通过这节课的学习,我们不仅掌握了探究问题的方法,还加深了长方体和正方体的在我们脑海中的空间观念,这对我们后继的学习帮助非常大。同学们都很帮,请继续努力吧!
本课结束
长方体和正方体的体积
苏教版六年级上
教学目标
在实际操作中,自主探索并掌握长方体和正方体体积公式,能应用公式正确计算长方体和正方体的体积,并能解决一些简单的实际问题。
通过操作、观察、猜想和归纳的探索过程,不断积累立体图形的学习经验,增强空间观念,发展数学思维。
进一步体会数学与生活的联系,获得数学成就感。
巩固复习与情景导入
把它割成1立方厘米的小正方体。
同学说得对,要知道一个物体的体积,就是要看这个物体中包含了多少个体积单位
4cm
3cm
2cm
同学们,上节课我们学习了体积和体积单位,今天老师带来了一个用1立方厘米的小正方体摆成的长方体,你有办法知道这个长方体的体积是多少立方厘米吗?
把它分割过后如左图,按长方体模型的长、宽、高分割,算出长方体的体积。它有24个体积单位,所以是24立方厘米。
老师的这个长方体模型是用1立方厘米的小正方体摆成的可以分割,但在生活中很多长方体或正方体的物体是不能分割的,如长方体礼盒、文具盒、石块等,它们的体积又有什么办法知道呢?这节课我们一起来研究长方体和正方体的体积计算方法吧。
拿出准备好的长方体,想一想长方体的体积可能与它的什么有关?我们可以用怎样的方法研究长方体的体积?
新授知识
长方体的体积应该与它的长、宽、高有关。
可以把长方体分割成若干个棱长1厘米,1分米或1米的正方体长方体中含有体积单位的个数,算出体积,再和它们的长、宽、高进行比较。
新授知识
同学们说的有道理,方法也不错,但我们需要实验研究才能证明长方体的体积和它的长宽高到底有怎样的关系。
操作探究
操作要求:
1、同桌合作用若干个1立方厘米的正方体,任意摆出四个不同的长方体,并编上序号。
2、观察摆出的长方体的长宽高所用,小正方体的个数,以及它们的体积各是多少?
3、填完表格后,同桌核对数据,并交流自己的发现。
操作探究
长(cm)
宽(cm)
高(cm)
小正方体的个数
体积(cm?)
长方体1
长方体2
长方体3
长方体4
1
2
3
4
3
2
3
18
18
2
2
2
8
8
4
3
2
24
24
2
2
4
16
16
同学们真棒,通过把长方体模型分割的方法,验证了长方体的体积与它长宽高的关系,进而发现了长方体的体积等于它的长宽高的乘积。
我们组摆的是长宽高分别是4,3和2,第一层横着的有4个,竖着的有3个,一共12个,一共有两层,所以是24个,也就是24立方厘米,计算结果和它们的长宽高相乘一致。
长方体的体积=长×宽×高
以后我们可以直接用公式计算长方体的体积,如果用v表示长方体的体积,a、b、h分别表示长方体的长、宽、高,你能用字母表示出长方体的体积公式吗?
长方体的体积=长×宽×高
V=abh
我们都知道正方体是特殊的长方体,想想看正方体的棱长有什么特点?你能直接写出正方体的体积公式吗?
正方体的棱长都相等,所以
正方体的体积=棱长×棱长×棱长
如果正方体的棱长用a表示,你能写出它的公式吗?
V=a?a?a
a?a?a也可以写成a?,读作a的立方,a?表示三个a相乘,正方体的体积公式,一般写成
v=a?
巩固练习
1、计算下面长方体和正方体的体积
10cm
4cm
5cm
2dm
2.2dm
4.5dm
2dm
8cm
8cm
2cm
2.2m
2.2m
2.2m
答:10×5×4=200(cm?)
2×2.2×4.5=19.8(dm?)
8×8×2=128(cm?)
2.2?=10.648(m?)
2、计算
3?=
5?=
10?=
1?=
0.1?=
27
125
1000
1
0.001
3、一种货车的车厢是长方体,从里面量长是5米,宽是1.8米,高是2米,它的容积是多少立方米?
5×1.8×2=18(立方米)
答:它的容积是18立方米。
4、一块正方体木料棱长4分米,这块木料的体积是多少立方分米?如果一立方分米的木料重1.5千克,这块木料重多少千克?
4?=64(立方分米)
64×1.5=96(千克)
答:这块木料的体积是64立方分米,
这块木料重96千克.
本课总结
今天我们一起学习了长方体和正方体体积的计算方法,通过这节课的学习,我们不仅掌握了探究问题的方法,还加深了长方体和正方体的在我们脑海中的空间观念,这对我们后继的学习帮助非常大。同学们都很帮,请继续努力吧!
本课结束
