1.1集合复习课件(第三课时)-2021-2022学年高一上学期数学北师大版(2019)必修一(共40张PPT)
文档属性
| 名称 | 1.1集合复习课件(第三课时)-2021-2022学年高一上学期数学北师大版(2019)必修一(共40张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-29 14:39:18 | ||
图片预览



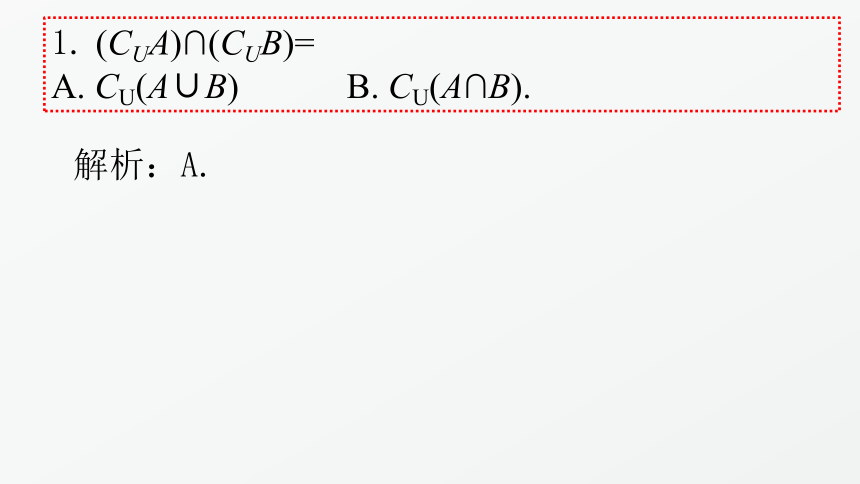








文档简介
(共40张PPT)
第二课时
第一章集合复习
北师大(2019)必修1
看看这一节我们要学什么
1.知识板块:全集与补集理论
2.技能板块:补集相关运
算
3.素养板块:由补集运算求参
环节一
全集
和补集理论
1.
(CUA)∩(CUB)=
A.
CU(A∪B)
B.
CU(A∩B).
解析:A.
2.
(CUA)∪(CUB)=
A.
CU(A∪B)
B.
CU(A∩B).
解:B
3.N∩?IM=?,所以N
M
A.
?
B.
C.=
解:选A。
4.
N∩?IM=N,说明()
?
A.
C.
解:选C。
环节二
补集相关运算
【角度一
有限集之间】
1.设全集U=R,集合A={x|0A.3个
B.4个 C.5个
D.6个
【解析】因为U=R,A={x|0【角度一
有限集之间】
2.已知全集U={1,2,3,4,5},集合A={x|x2-3x+2=0},B={x|x=2a,a∈A},则集合?U(A∪B)中元素的个数为( )
A.1个
B.2个
C.3个
D.4个
【解析】A={1,2},B={x|x=2a,a∈A}={2,4},∴A∪B={1,2,4},∴?U(A∪B)={3,5}.故选B.
3.全集U={1,2,3,4,5,6},集合A={x|x2-3x+2=0},B={x|x=2a,a∈A},则集合?U(A∪B)的子集个数为( )
A.1
B.3 C.4
D.8
【解析】A={x|x2-3x+2=0}={1,2},则B={x|x=2a,a∈A}={2,4},故A∪B={1,2,4}.又全集U={1,2,3,4,5,6},则?U(A∪B)={3,5,6},含有3个元素,其子集个数为23=8.故选D..
【角度一
有限集之间】
4.已知全集U={1,2,3,4,5,6},集合A={1,2,5},?UB={4,5,6},则A∩B=( )
A.{1,2}
B.{5}
C.{1,2,3}
D.{3,4,6}
解析:因为?UB={4,5,6},所以B={1,2,3},所以A∩B={1,2,5}∩{1,2,3}={1,2},故选A.
【角度一
有限集之间】
5.已知全集U={0,1,2,3,4},集合A={1,2,3},B={2,4},则(?UA)∪B为( C )
A.{1,2,4}
B.{2,3,4}
C.{0,2,4}
D.{0,2,3,4}
解析:?UA={0,4},所以(?UA)∪B={0,4}∪{2,4}={0,2,4}.
【角度一
有限集之间】
6.已知全集U={0,1,2,3,4,5,6,7,8,9},集合A={0,1,3,5,8},集合B={2,4,5,6,8},则(?UA)∩(?UB)=( B )
A.{5,8}
B.{7,9}
C.{0,1,3}
D.{2,4,6}
解析:根据集合运算的性质求解.因为A∪B={0,1,2,3,4,5,6,8},所以(?UA)∩(?UB)=?U(A∪B)={7,9}.
【角度一
有限集之间】
7.若全集U={0,1,2,3}且?UA={2},则集合A的真子集共有( )
A.3个
B.5个
C.7个
D.8个
解析:C [A={0,1,3},真子集有23-1=7.]
【角度一
有限集之间】
8.设全集U=R,A={x|x>0},B={x|x>1},则A∩(?UB)=________.
A.
{x|0B.
{x|0≤x≤1}
C.
{x|x≥1}
D.
{x|x≤0}
【解析】∵U=R,B={x|x>1},∴?UB={x|x≤1}.又A={x|x>0},∴A∩(?UB)={x|x>0}∩{x|x≤1}={x|0【角度二
无限集之间】
9.设集合S={x|x>-2},T={x|x2+3x-4≤0},则(?RS)∪T=( C )
A.{x|-2B.{x|x≤-4}
C.{x|x≤1}
D.{x|x≥1}
解析:因为?RS={x|x≤-2},T={x|x2+3x-4≤0}={x|-4≤x≤1},所以(?RS)∪T={x|x≤1}.故选C.
【角度二
无限集之间】
10.设全集U为实数集R,M={x|x>2或x<-2},N={x|x≥3或x<1}都是全集U的子集,则图中阴影部分所表示的集合是( )
A.{x|-2≤x<1}
B.{x|-2≤x≤2}
C.{x|1D.{x|x<2}
【角度二
无限集之间】
A [阴影部分表示的集合为N∩(?UM)={x|-2≤x<1},故选A.]
11.设全集U是实数集R,M={x|x<-2,或x>2},N={x|1≤x≤3}.如图所示,则阴影部分所表示的集合为()
A.
{x|-2≤x<1}
B.
{x|}
C.
{x|-1≤x<2}
D.{x|-3≤x<2}
【角度二
无限集之间】
解:阴影部分所表示的集合为?U(M∪N)=(?UM)∩(?UN)={x|-2≤x≤2}∩{x|x<1或x>3}={x|-2≤x<1}.
角度三符号集之间
12.如图,已知I是全集,A,B,C是它的子集,则阴影部分所表示的集合是( )
A.(?IA∩B)∩C
B.(?IB∪A)∩C
C.(A∩B)∩(?IC)
D.(A∩?IB)∩C
【解析】由题图可知阴影部分中的元素属于A,不属于B,属于C,则阴影部分表示的集合是(A∩?IB)∩C.
角度三符号集之间
13.如图,I是全集,M,P,S是I的3个子集,则阴影部分所表示的集合是( )
A.(M∩P)∩S
B.(M∩P)∪S
C.(M∩P)∪(?IS)
D.(M∩P)∩(?IS)
解析:由题图,可知阴影部分是M与P除S外的公共部分,所以阴影部分所表示的集合是(M∩P)∩(?IS).故选D.
角度三符号集之间
14.已知M,N为集合I的非空真子集,且M,N不相等,若N∩?IM=?,则M∪N=( )
A.M
B.N
C.I
D.?
解析:因为N∩?IM=?,所以N?M,所以M∪N=M.故选A.
角度三符号集之间
15.图中阴影部分所表示的集合是( )
A.B∩(?U(A∪C))
B.(A∪B)∪(B∪C)
C.(A∪C)∩(?UB)
D.(?U(A∩C))∪B
解析:阴影部分位于集合B内,且位于集合A、C的外部,故可表示为B∩(?U(A∪C)).故选A.
角度三符号集之间
解析:根据定义“x∈M,且x?P”等价于“x∈M∩(?UP)”.为此引入全集U,则有M-P=M∩(?UP).于是有M-(M-P)=M-[M∩(?UP)]=M∩[?U(M∩?UP)]=M∩{(?UM)∪[?U(?UP)]}=M∩[(?UM)∪P]=[M∩(?UM)]∪(M∩P)=?∪(M∩P)=M∩P.(如图所示)
16.设M、P是两个非空集合,定义M与P的差集为:M-P={x|x∈M且x?P},那么集合M-(M-P)=
A.P
B.N
C.M
D.
角度三符号集之间
解析 由图易知,A正确;?
由A∪B=?,得A=B=?,B正确;由Venn图易知C正确.故选D.
17.下列四个命题中,设U为全集,则不正确的命题是( )
A.若A∩B=?,则(?UA)∪(?UB)=U
B.若A∪B=?,则A=B=?
C.若A∪B=U,则(?UA)∩(?UB)=?
D.若A∩B=?,则A=B=?
环节三
补集运算求参
1.
已知全集U={1,2,a2-2a+3},A={1,a},?UA={3},则实数a等于( )
A.0或2
B.0
C.1或2
D.2
角度一
有限集求参
【解析】由题意知则a=2.则a=2
2.设U=R,集合A={x|x2-x-2=0},B={x|x2+mx+m-1=0}.若(?UA)∩B=?,求实数m的取值.
A.2
B.-1
C.2,-1
D.-2,1
角度一
有限集求参
解:解方程x2-x-2=0,即(x+1)(x-2)=0,解得x=-1或x=2.故A={-1,2}.由(?UA)∩B=?可知,B?A.方程x2+mx+m-1=0的判别式Δ=m2-4×1×(m-1)=(m-2)2≥0.
2.设U=R,集合A={x|x2-x-2=0},B={x|x2+mx+m-1=0}.若(?UA)∩B=?,求实数m的取值.
A.2
B.-1
C.2,-1
D.-2,1
角度一
有限集求参
①当Δ=0,即m=2时,方程x2+mx+m-1=0为x2+2x+1=0,解得x=-1,故B={-1}.
此时满足B?A.
2.设U=R,集合A={x|x2-x-2=0},B={x|x2+mx+m-1=0}.若(?UA)∩B=?,求实数m的取值.
A.2
B.-1
C.2,-1
D.-2,1
角度一
有限集求参
②当Δ>0,即m≠2时,方程x2+mx+m-1=0有两个不同的解,故集合B中有两个元素.又因为B?A,且A={-1,2},所以A=B.故-1,2为方程x2+mx+m-1=0的两个解,由根与系数之间的关系可得解得m=-1.
综上,m的取值为2或-1.
3.已知集合A={x|xA.
{a|a≥1}
B.
{a|a≥2}
C.
{a|a≥3}
角度二无限集求参
【解析】∵B={x|14.已知集合A={x|-4≤x≤-2},集合B={x|x-a≥0}.若全集U=R,且A?(?UB),求实数a的取值范围.A.
角度二无限集求参
∵U=R,∴?UB={x|x<a}.要使A??UB,即a>-2.
5.已知集合A={x|-1<x≤3},B={x|m≤x<1+3m}
若B??RA,求实数m的取值范围.
A.
.
B.
.
C.
D.
角度二无限集求参
?RA={x|x≤-1或x>3}.
当B=?时,即m≥1+3m,得m≤,满足B??RA.
当B≠?时,使B??RA成立,且
或解得m>3.
综上可知,实数m的取值范围是
.
6.已知集合A={x|x>2},B={x|x<2m},且A??RB,那么m的取值范围是
?
A.
m≤1.
B.
m>1
C.
m≤2
角度二无限集求参
解析:由B={x|x<2m},得?RB={x|x≥2m},
∵A??RB,∴2m≤2,∴m≤1.
7.已知集合A={x|2≤x<7},B={x|3?
A.
a≤1,
B.
a≤2,
C.
1角度二无限集求参
解析:因为A={x|2≤x<7},C={x|x且A∩C=?,所以a≤2,
即实数a的取值范围为{a|a≤2}.
8.设全集U=R,集合A={x|x≤1,或x≥3},集合B={KA.k<0或k>3
B.2C.0D.-1角度二无限集求参
解析:因为?UA
={x|1得
9.已知集合A={x|x<a},B={x|1<x<2},且A∪(?RB)=R,则实数a的取值范围是( )
A.{a|a≤1}
B.{a|a<1}
C.{a|a≥2}
D.{a|a>2}
角度二无限集求参
解析:C [由于A∪(?RB)=R,则B?A,可知a≥2.故选C.]
10.M={x|x<-2或x>2},N={x|x≤m},若(?RM)∩N≠?,则实数m的取值范围为( )
A.m<2
B.m≥-2
C.m>-1
D.-2≤m≤2
角度二无限集求参
解析 ?RM={x|-2≤x≤2},再利用数轴来解决(?RM)∩N≠?时m的取值范围,易知m≥-2.?
谢谢观看
第二课时
第一章集合复习
北师大(2019)必修1
看看这一节我们要学什么
1.知识板块:全集与补集理论
2.技能板块:补集相关运
算
3.素养板块:由补集运算求参
环节一
全集
和补集理论
1.
(CUA)∩(CUB)=
A.
CU(A∪B)
B.
CU(A∩B).
解析:A.
2.
(CUA)∪(CUB)=
A.
CU(A∪B)
B.
CU(A∩B).
解:B
3.N∩?IM=?,所以N
M
A.
?
B.
C.=
解:选A。
4.
N∩?IM=N,说明()
?
A.
C.
解:选C。
环节二
补集相关运算
【角度一
有限集之间】
1.设全集U=R,集合A={x|0
B.4个 C.5个
D.6个
【解析】因为U=R,A={x|0
有限集之间】
2.已知全集U={1,2,3,4,5},集合A={x|x2-3x+2=0},B={x|x=2a,a∈A},则集合?U(A∪B)中元素的个数为( )
A.1个
B.2个
C.3个
D.4个
【解析】A={1,2},B={x|x=2a,a∈A}={2,4},∴A∪B={1,2,4},∴?U(A∪B)={3,5}.故选B.
3.全集U={1,2,3,4,5,6},集合A={x|x2-3x+2=0},B={x|x=2a,a∈A},则集合?U(A∪B)的子集个数为( )
A.1
B.3 C.4
D.8
【解析】A={x|x2-3x+2=0}={1,2},则B={x|x=2a,a∈A}={2,4},故A∪B={1,2,4}.又全集U={1,2,3,4,5,6},则?U(A∪B)={3,5,6},含有3个元素,其子集个数为23=8.故选D..
【角度一
有限集之间】
4.已知全集U={1,2,3,4,5,6},集合A={1,2,5},?UB={4,5,6},则A∩B=( )
A.{1,2}
B.{5}
C.{1,2,3}
D.{3,4,6}
解析:因为?UB={4,5,6},所以B={1,2,3},所以A∩B={1,2,5}∩{1,2,3}={1,2},故选A.
【角度一
有限集之间】
5.已知全集U={0,1,2,3,4},集合A={1,2,3},B={2,4},则(?UA)∪B为( C )
A.{1,2,4}
B.{2,3,4}
C.{0,2,4}
D.{0,2,3,4}
解析:?UA={0,4},所以(?UA)∪B={0,4}∪{2,4}={0,2,4}.
【角度一
有限集之间】
6.已知全集U={0,1,2,3,4,5,6,7,8,9},集合A={0,1,3,5,8},集合B={2,4,5,6,8},则(?UA)∩(?UB)=( B )
A.{5,8}
B.{7,9}
C.{0,1,3}
D.{2,4,6}
解析:根据集合运算的性质求解.因为A∪B={0,1,2,3,4,5,6,8},所以(?UA)∩(?UB)=?U(A∪B)={7,9}.
【角度一
有限集之间】
7.若全集U={0,1,2,3}且?UA={2},则集合A的真子集共有( )
A.3个
B.5个
C.7个
D.8个
解析:C [A={0,1,3},真子集有23-1=7.]
【角度一
有限集之间】
8.设全集U=R,A={x|x>0},B={x|x>1},则A∩(?UB)=________.
A.
{x|0
{x|0≤x≤1}
C.
{x|x≥1}
D.
{x|x≤0}
【解析】∵U=R,B={x|x>1},∴?UB={x|x≤1}.又A={x|x>0},∴A∩(?UB)={x|x>0}∩{x|x≤1}={x|0
无限集之间】
9.设集合S={x|x>-2},T={x|x2+3x-4≤0},则(?RS)∪T=( C )
A.{x|-2
C.{x|x≤1}
D.{x|x≥1}
解析:因为?RS={x|x≤-2},T={x|x2+3x-4≤0}={x|-4≤x≤1},所以(?RS)∪T={x|x≤1}.故选C.
【角度二
无限集之间】
10.设全集U为实数集R,M={x|x>2或x<-2},N={x|x≥3或x<1}都是全集U的子集,则图中阴影部分所表示的集合是( )
A.{x|-2≤x<1}
B.{x|-2≤x≤2}
C.{x|1
【角度二
无限集之间】
A [阴影部分表示的集合为N∩(?UM)={x|-2≤x<1},故选A.]
11.设全集U是实数集R,M={x|x<-2,或x>2},N={x|1≤x≤3}.如图所示,则阴影部分所表示的集合为()
A.
{x|-2≤x<1}
B.
{x|}
C.
{x|-1≤x<2}
D.{x|-3≤x<2}
【角度二
无限集之间】
解:阴影部分所表示的集合为?U(M∪N)=(?UM)∩(?UN)={x|-2≤x≤2}∩{x|x<1或x>3}={x|-2≤x<1}.
角度三符号集之间
12.如图,已知I是全集,A,B,C是它的子集,则阴影部分所表示的集合是( )
A.(?IA∩B)∩C
B.(?IB∪A)∩C
C.(A∩B)∩(?IC)
D.(A∩?IB)∩C
【解析】由题图可知阴影部分中的元素属于A,不属于B,属于C,则阴影部分表示的集合是(A∩?IB)∩C.
角度三符号集之间
13.如图,I是全集,M,P,S是I的3个子集,则阴影部分所表示的集合是( )
A.(M∩P)∩S
B.(M∩P)∪S
C.(M∩P)∪(?IS)
D.(M∩P)∩(?IS)
解析:由题图,可知阴影部分是M与P除S外的公共部分,所以阴影部分所表示的集合是(M∩P)∩(?IS).故选D.
角度三符号集之间
14.已知M,N为集合I的非空真子集,且M,N不相等,若N∩?IM=?,则M∪N=( )
A.M
B.N
C.I
D.?
解析:因为N∩?IM=?,所以N?M,所以M∪N=M.故选A.
角度三符号集之间
15.图中阴影部分所表示的集合是( )
A.B∩(?U(A∪C))
B.(A∪B)∪(B∪C)
C.(A∪C)∩(?UB)
D.(?U(A∩C))∪B
解析:阴影部分位于集合B内,且位于集合A、C的外部,故可表示为B∩(?U(A∪C)).故选A.
角度三符号集之间
解析:根据定义“x∈M,且x?P”等价于“x∈M∩(?UP)”.为此引入全集U,则有M-P=M∩(?UP).于是有M-(M-P)=M-[M∩(?UP)]=M∩[?U(M∩?UP)]=M∩{(?UM)∪[?U(?UP)]}=M∩[(?UM)∪P]=[M∩(?UM)]∪(M∩P)=?∪(M∩P)=M∩P.(如图所示)
16.设M、P是两个非空集合,定义M与P的差集为:M-P={x|x∈M且x?P},那么集合M-(M-P)=
A.P
B.N
C.M
D.
角度三符号集之间
解析 由图易知,A正确;?
由A∪B=?,得A=B=?,B正确;由Venn图易知C正确.故选D.
17.下列四个命题中,设U为全集,则不正确的命题是( )
A.若A∩B=?,则(?UA)∪(?UB)=U
B.若A∪B=?,则A=B=?
C.若A∪B=U,则(?UA)∩(?UB)=?
D.若A∩B=?,则A=B=?
环节三
补集运算求参
1.
已知全集U={1,2,a2-2a+3},A={1,a},?UA={3},则实数a等于( )
A.0或2
B.0
C.1或2
D.2
角度一
有限集求参
【解析】由题意知则a=2.则a=2
2.设U=R,集合A={x|x2-x-2=0},B={x|x2+mx+m-1=0}.若(?UA)∩B=?,求实数m的取值.
A.2
B.-1
C.2,-1
D.-2,1
角度一
有限集求参
解:解方程x2-x-2=0,即(x+1)(x-2)=0,解得x=-1或x=2.故A={-1,2}.由(?UA)∩B=?可知,B?A.方程x2+mx+m-1=0的判别式Δ=m2-4×1×(m-1)=(m-2)2≥0.
2.设U=R,集合A={x|x2-x-2=0},B={x|x2+mx+m-1=0}.若(?UA)∩B=?,求实数m的取值.
A.2
B.-1
C.2,-1
D.-2,1
角度一
有限集求参
①当Δ=0,即m=2时,方程x2+mx+m-1=0为x2+2x+1=0,解得x=-1,故B={-1}.
此时满足B?A.
2.设U=R,集合A={x|x2-x-2=0},B={x|x2+mx+m-1=0}.若(?UA)∩B=?,求实数m的取值.
A.2
B.-1
C.2,-1
D.-2,1
角度一
有限集求参
②当Δ>0,即m≠2时,方程x2+mx+m-1=0有两个不同的解,故集合B中有两个元素.又因为B?A,且A={-1,2},所以A=B.故-1,2为方程x2+mx+m-1=0的两个解,由根与系数之间的关系可得解得m=-1.
综上,m的取值为2或-1.
3.已知集合A={x|x
{a|a≥1}
B.
{a|a≥2}
C.
{a|a≥3}
角度二无限集求参
【解析】∵B={x|1
角度二无限集求参
∵U=R,∴?UB={x|x<a}.要使A??UB,即a>-2.
5.已知集合A={x|-1<x≤3},B={x|m≤x<1+3m}
若B??RA,求实数m的取值范围.
A.
.
B.
.
C.
D.
角度二无限集求参
?RA={x|x≤-1或x>3}.
当B=?时,即m≥1+3m,得m≤,满足B??RA.
当B≠?时,使B??RA成立,且
或解得m>3.
综上可知,实数m的取值范围是
.
6.已知集合A={x|x>2},B={x|x<2m},且A??RB,那么m的取值范围是
?
A.
m≤1.
B.
m>1
C.
m≤2
角度二无限集求参
解析:由B={x|x<2m},得?RB={x|x≥2m},
∵A??RB,∴2m≤2,∴m≤1.
7.已知集合A={x|2≤x<7},B={x|3
A.
a≤1,
B.
a≤2,
C.
1
解析:因为A={x|2≤x<7},C={x|x
即实数a的取值范围为{a|a≤2}.
8.设全集U=R,集合A={x|x≤1,或x≥3},集合B={K
B.2
解析:因为?UA
={x|1
9.已知集合A={x|x<a},B={x|1<x<2},且A∪(?RB)=R,则实数a的取值范围是( )
A.{a|a≤1}
B.{a|a<1}
C.{a|a≥2}
D.{a|a>2}
角度二无限集求参
解析:C [由于A∪(?RB)=R,则B?A,可知a≥2.故选C.]
10.M={x|x<-2或x>2},N={x|x≤m},若(?RM)∩N≠?,则实数m的取值范围为( )
A.m<2
B.m≥-2
C.m>-1
D.-2≤m≤2
角度二无限集求参
解析 ?RM={x|-2≤x≤2},再利用数轴来解决(?RM)∩N≠?时m的取值范围,易知m≥-2.?
谢谢观看
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
