5.7三角函数的应用课后练习——2021-2022学年高一上学期数学人教A版(2019)必修第一册第五章三角函数第七节(Word含答案解析)
文档属性
| 名称 | 5.7三角函数的应用课后练习——2021-2022学年高一上学期数学人教A版(2019)必修第一册第五章三角函数第七节(Word含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 163.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-29 15:14:54 | ||
图片预览



文档简介
第五章三角函数第七节5.7三角函数的应用课后练习2021-2022学年高中数学人教A版2019必修第一册
一、单选题(共11题)
1.在一幢20m高的楼顶,测得对面一塔吊顶的仰角为
,
塔基的俯角为
,
那么塔吊的高是(??)
A.??????????????B.??????????????C.??????????????D.?
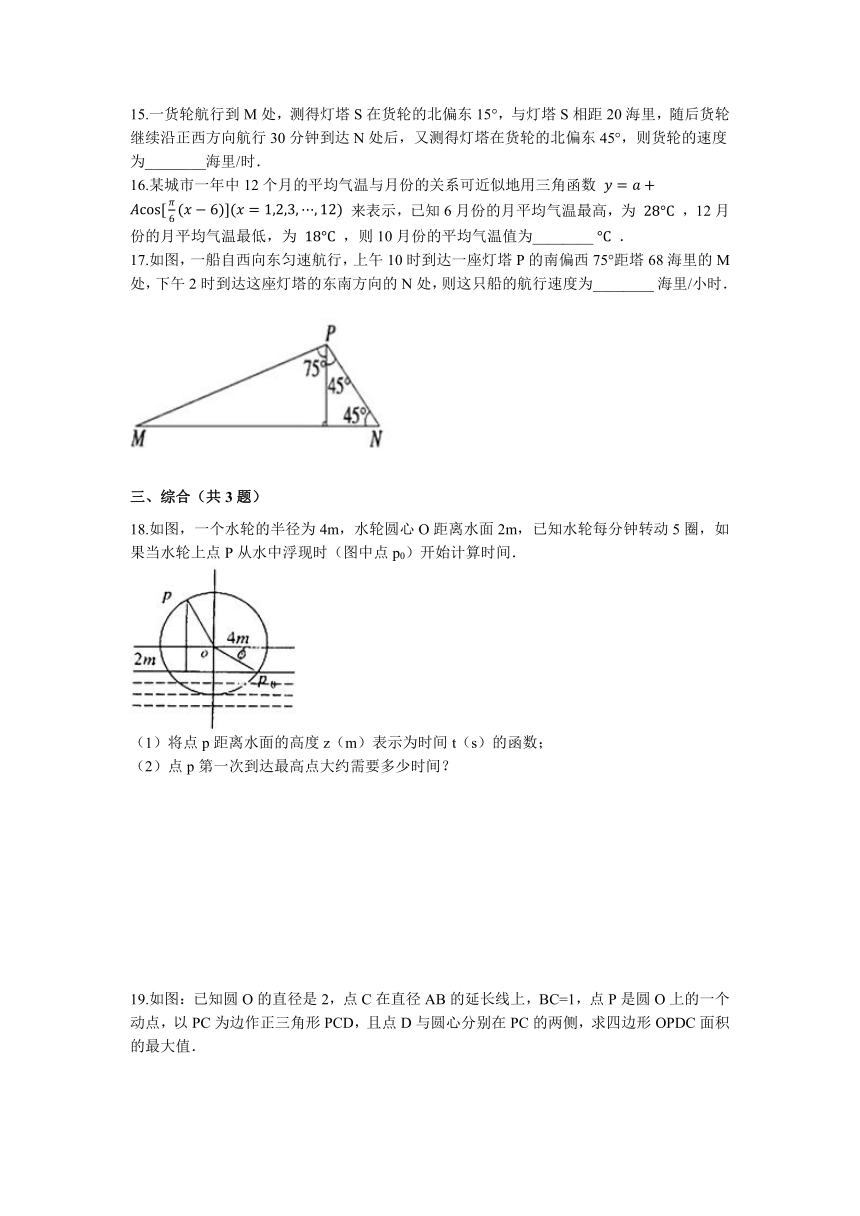
2.已知两座灯塔A和B与海洋观察站C的距离都等于a
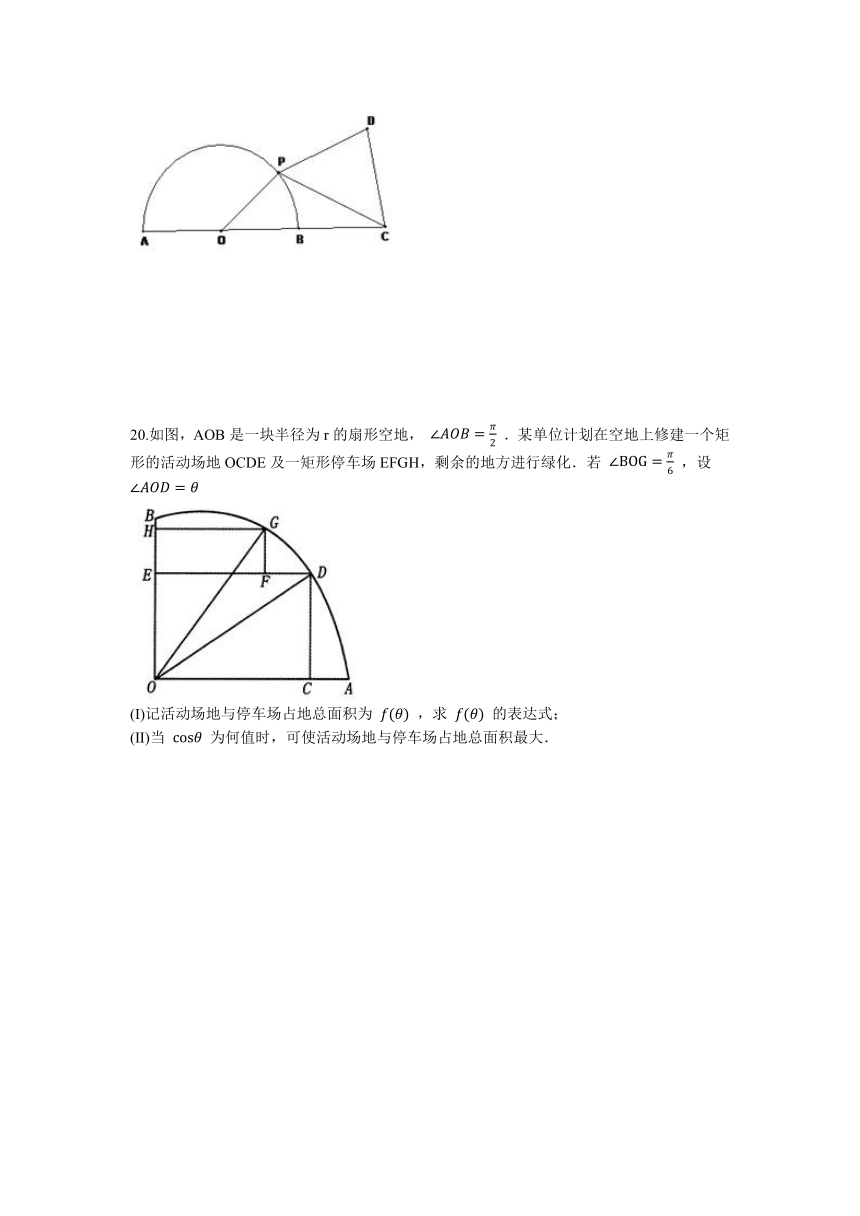
km,灯塔A在观察站C的北偏东20°,灯塔B在观察站C的南偏东40°,则灯塔A与B的距离为(?
)
A.?akm????????????????????????????????B.?akm
????????????????????????????????C.?akm????????????????????????????????D.?2akm
3.函数的部分图象如图,则(?
)
A.?????????????????B.?????????????????C.?????????????????D.?
4.水车在古代是进行灌溉引水的工具,是人类的一项古老的发明,也是人类利用自然和改造自然的象征.如图是一个半径为R的水车,一个水斗从点A(3
,﹣3)出发,沿圆周按逆时针方向匀速旋转,且旋转一周用时60秒.经过t秒后,水斗旋转到P点,设P的坐标为(x,y),其纵坐标满足y=f(t)=Rsin(ωt+φ)(t≥0,ω>0,|φ|<
).则下列叙述错误的是(??
)
A.???????????????????????????????????B.?当t∈[35,55]时,点P到x轴的距离的最大值为6
C.?当t∈[10,25]时,函数y=f(t)单调递减?????????D.?当t=20时,
5.已知
sinα+
cosα=2,则tanα=(
??)
A.?-
????????????????????????????????????B.?????????????????????????????????????C.?-
????????????????????????????????????D.?
6.设动直线x=a与函数f(x)=2sin2(
+x)和g(x)=
cos2x的图象分别交于M、N两点,则|MN|的最大值为(??
)
A.??????????????????????????????????????????B.??????????????????????????????????????????C.?2?????????????????????????????????????????D.?3
7.要测量底部不能到达的电视塔AB的高度,在C点测得塔顶A的仰角是45°,在D点测得塔顶A的仰角是30°,并测得水平面上的∠BCD=120°,CD=40m,则电视塔的高度为(?
)
A.?10
m???????????????????????????????B.?20m???????????????????????????????C.?20
m???????????????????????????????D.?40m
8.在一个港口,相邻两次高潮发生的时间相距12h,低潮时水深为9m,高潮时水深为15m.每天潮涨潮落时,该港口水的深度y(m)关于时间t(h)的函数图象可以近似地看成函数y=Asin(ωt+φ)+k的图象,其中0≤t≤24,且t=3时涨潮到一次高潮,则该函数的解析式可以是(??
)
A.??????????B.??????????C.??????????D.?
9.半径为1的球内切于一圆锥,则圆锥体积的最小值为( )
A.?2π???????????????????????????????????????B.????????????????????????????????????????C.?3π???????????????????????????????????????D.?
10.M,N是曲线y=πsinx与曲线y=πcosx的两个不同的交点,则|MN|的最小值为(?
)
A.?π?????????????????????????????????????B.??????????????????????????????????????C.??????????????????????????????????????D.?2π
11.矩形ABCD满足AB=2,AD=1,点A、B分别在射线OM,ON上,∠MON为直角,当C到点O的距离最大时,∠BAO的大小为( )
A.??????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?
二、填空题(共6题)
12.如图所示,PA,PB是⊙O的切线,AC是⊙O的直径,∠P=40°,则∠BAC=________.
13.某港口在一天24小时内的潮水的高度近似满足关系
,其中0≤t≤24,S的单位是m,t的单位是h,则18点时潮水起落的速度是________.
14.某城市一年中12个月的平均气温与月份的关系可近似地用三角函数
(x=1,2,3,…,12)来表示,已知6月份的月平均气温最高,为28℃,12月份的月平均气温最低,为18℃,则10月份的平均气温值为________℃
15.一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与灯塔S相距20海里,随后货轮继续沿正西方向航行30分钟到达N处后,又测得灯塔在货轮的北偏东45°,则货轮的速度为________海里/时.
16.某城市一年中12个月的平均气温与月份的关系可近似地用三角函数
来表示,已知6月份的月平均气温最高,为
,12月份的月平均气温最低,为
,则10月份的平均气温值为________
.
17.如图,一船自西向东匀速航行,上午10时到达一座灯塔P的南偏西75°距塔68海里的M处,下午2时到达这座灯塔的东南方向的N处,则这只船的航行速度为________?海里/小时.
三、综合(共3题)
18.如图,一个水轮的半径为4m,水轮圆心O距离水面2m,已知水轮每分钟转动5圈,如果当水轮上点P从水中浮现时(图中点p0)开始计算时间.
(1)将点p距离水面的高度z(m)表示为时间t(s)的函数;
(2)点p第一次到达最高点大约需要多少时间?
19.如图:已知圆O的直径是2,点C在直径AB的延长线上,BC=1,点P是圆O上的一个动点,以PC为边作正三角形PCD,且点D与圆心分别在PC的两侧,求四边形OPDC面积的最大值.
20.如图,AOB是一块半径为r的扇形空地,
.某单位计划在空地上修建一个矩形的活动场地OCDE及一矩形停车场EFGH,剩余的地方进行绿化.若
,设
(Ⅰ)记活动场地与停车场占地总面积为
,求
的表达式;
(Ⅱ)当
为何值时,可使活动场地与停车场占地总面积最大.
答案解析部分
一、单选题
1.【答案】
B
【解析】【解答】由题意,AB=20米,∠DAE=60°,∠DAC=45°,可知ABCD是正方形,有此易得CD=AD=20米,再由,∠DAE=60°,在直角三角形ADE中可求得DE=,
AD=20∴塔高为DE+CD="20+20"
=20(+1)故选B
【分析】本题考查已知三角函数模型的应用问题,解答本题的关键是建立起符合条件的模型,然后再由三角形中的相关知识进行运算,解三角形的应用一般是求距离(长度问题,高度问题等)解题时要注意综合利用所学的知识与题设中的条件,求解三角形的边与角
2.【答案】
B
【解析】解答:由图可知,∠ACB=120°,
由余弦定理
cos∠ACB=
=
=﹣
,
则AB=
a(km).
故选B.
分析:先根据题意确定∠ACB的值,再由余弦定理可直接求得|AB|的值.
3.【答案】
C
【解析】【解答】观察图象可知,A=1,T=4(3-1)=8,所以。将(1,1)代入得所以,
故选C。
4.【答案】C
【解析】【解答】解:由题意,R=
=6,T=60=
,∴ω=
,
点A(3
,﹣3)代入可得﹣3=6sinφ,∵|φ|<
),∴φ=﹣
.故A正确;
f(t)=6sin(
t﹣
),当t∈[35,55]时,
t﹣
∈[π,
],∴点P到x轴的距离的最大值为6,正确;
当t∈[10,25]时,
t﹣
∈[
π,
],函数y=f(t)单调递减,不正确;
当t=20时,
t﹣
=
,P的纵坐标为6,|PA|=
=6
,正确,
故选C.
【分析】求出函数的解析式,再分析选项,即可得出结论.
5.【答案】
D
【解析】【解答】解:∵
sinα+??cosα=2
,
∴
,
可得
,
∴
,
.
∴
,
则.
故答案为:D
【分析】sinα+??cosα=2
,
利用和差公式化简可得
,
即可求出的值。
6.【答案】
D
【解析】【解答】解:
,
=
.
故选D
【分析】利用二倍角公式先化简f(x),将|MN|表示成a的三角函数,利用公式
化简|MN|,利用三角函数的有界性求出最大值.
7.【答案】
D
【解析】解答:由题可设AB=x
,
则
,
在△DBC中,∠BCD=120°,CD=40,由余弦定理得BD2=BC2+CD2﹣2BC?CD?cos∠DCB
即:(
)2=(40)2+x2﹣2×40?x?cos120°
整理得:x2﹣20x﹣800=0
解得x=40或x=﹣20(舍)
所以,所求塔高为40米
.
故选D.
分析:设出AD=x
,
进而根据题意可表示出BD,DC,进而在△DBC中利用余弦定理建立方程求得x
.
8.【答案】A
【解析】【解答】解:依题意,
,解得
,
又T=
,
∴ω=
.
又f(3)=15,
∴3sin(
+φ)+12=15,
∴sin(
+φ)=1.
∴φ=0,
∴y=f(t)=3sin
t+12.
故选:A.
【分析】高潮时水深为A+K,低潮时水深为﹣A+K,联立方程组求得A和K的值,再由相邻两次高潮发生的时间相距12h,可知周期为12,由此求得ω值,再结合t=3时涨潮到一次高潮,把点(3,15)代入y=Asin(ωx+φ)+K的解析式求得φ,则函数y=f(t)的表达式可求.
9.【答案】
B
【解析】【解答】解:设母线与底面的夹角2α,底面半径R,内切球半径r=1,圆锥的高h
则:R=r?cotα=cotα,h=R?tan2α=cotα?tan2α=
,
圆锥的体积
=
,
而2α<90°,α<45°,所以:tanα<1,1﹣tan2α>0
又因为:tan2α+(1﹣tan2α)=1=定值
所以:当tan2α=1﹣tan2α,即tanα=时,V最小=
.
故选B.
【分析】设母线与底面的夹角2α,底面半径R,内切球半径r=1,圆锥的高h用α表示R,h,求出圆锥的体积V的表达式,利用基本不等式求出V最小
.
10.【答案】
C
【解析】解答:要求|MN|的最小值在,只要在一个周期内解即可
∵πsinx=πcosx
解得x=
或x=
得到两个点为(,
)和(
)
得到|MN|=
=
故选C
分析:|MN|的最小值即一个周期内两个交点的距离;列出方程求出两个交点坐标,据两点的距离公式求出|MN|的最小值.
11.【答案】
D
【解析】【解答】解:如图所示,
建立直角坐标系.
设∠OAB=θ,则∠CBE=θ.
.
B(0,2sinθ),C(sinθ,cosθ+2sinθ).
∴|OC|2=sin2θ+(cosθ+2sinθ)2
=1+4sinθcosθ+4sin2θ
=1+2sin2θ+2(1﹣cos2θ)
=+3,
∵
,
∴
.
∴当2
,
即时,|OC|2取得最大值,2+3.
故选:D.
【分析】如图所示,建立直角坐标系.设∠OAB=θ,则∠CBE=θ.
.
可得B(0,2sinθ),C(sinθ,cosθ+2sinθ).|OC|2=sin2θ+(cosθ+2sinθ)2
=+3,由于
,
可得
.
即可得出.
二、填空题
12.【答案】
20°
【解析】【解答】连接OP,
根据切线的性质可知,AP=BP,∠DAP=∠DPB=
∠P=
×40°=20°,
在△ADP与△BPD中,AP=BP,DP=DP,∠DAP=∠DPB=20°,
∴△ADP≌△BPD,OP⊥AB,
∴∠DAP=90°﹣∠DAP=90°﹣20°=70°,
∵AP是⊙O的切线,AC是直径,
∴∠OAP=90°,
∴∠BAC=∠OAP﹣∠DAP=90°﹣70°=20°.
【分析】连接OP,根据切线的性质可求出△ADP≌△BPD及∠APD的度数,根据直角三角形的性质可求出∠DAP的度数,由切线的性质定理解答即可.
13.【答案】
【解析】【解答】由题意,∵
∴v=S'=
当t=18时,速度v=
故答案为
【分析】利用导数的物理意义,高度对时间的导数,从而得解.
14.【答案】
16
【解析】【解答】据题意得28=a+A,
=a﹣A
解得a=20,A=8
所以
令x=10得y=
=16
故答案为:16
【分析】根据题意列出方程组,求出a,A,求出年中12个月的平均气温与月份的关系可近似地用三角函数;将x=10代入求出10月份的平均气温值.
15.【答案】
【解析】【解答】由题意,如图所示,
可知∠SMN=15°+90°=105°,∠SNM=45°,SM=20,∴∠NSM=30°,
在△SMN中,由正弦定理可得:
,
即
,解得:MN=
,
∴货轮的速度为
=
海里/时.
故答案为:
.
【分析】由题意可知,在△SMN中,由正弦定理可得MN=
,
即可得出货轮的速度.
16.【答案】
20.5
【解析】【解答】根据题意,由于一年中12个月的平均气温与月份x的关系可近似地用三角函数y=a+Acos[
(x-6)](x=1,2,3,…,12),由于x=6,y=28,可知a+A=28,x=12,a-A=18,得到a=23,A=5,当x=10,y=20.5,故可知则10月份的平均气温值为20.5℃。
【分析】根据实际问题的已知条件结合三角型函数图象与a和A的关系,从而建立关于a和A的方程组,进而求出a和A的值,从而求出三角型函数的解析式,再利用三角型函数的解析式求出10月份的平均气温值。
17.【答案】
【解析】【解答】解:由题意知∠MPN=75°+45°=120°,∠PNM=45°.
在△PMN中,由正弦定理,得
,
∴MN=
又由M到N所用时间为14﹣10=4(小时),
∴船的航行速度v==(海里/时);
故答案为:
.
【分析】根据题意可求得∠MPN和,∠PNM进而利用正弦定理求得MN的值,进而求得船航行的时间,最后利用里程除以时间即可求得问题的答案.
三、综合题
18.【答案】
(1)解:依题意可知z的最大值为6,最小为﹣2,
∴
?
;
∵op每秒钟内所转过的角为
,得z=4sin
,
当t=0时,z=0,得sinφ=﹣
,即φ=﹣
,故所求的函数关系式为
z=4sin
+2
(2)解:令z=4sin
+2=6,得sin
=1,
取
,得t=4,
故点P第一次到达最高点大约需要4S
【解析】【分析】(1)先根据z的最大和最小值求得A和B,利用周期求得ω,当x=0时,z=0,进而求得φ的值,则函数的表达式可得;(2)令最大值为6,即
z=4sin
+2=6可求得时间.
19.【答案】
解:设∠POB=θ.在△POC中,由余弦定理得:PC2=OP2+OC2﹣2OP?OC?cosθ=5﹣4cosθ
所以
,
当时,即时,
四边形OPDC面积的最大值为
2+
.
【解析】【分析】设∠POB=θ,将面积表示为角的函数,再利用三角函数求最值的方法求最值.
20.【答案】
解:
Ⅰ
由题意得,在矩形OCDE中,
,
,
,
矩形OCDE的面积为
;
又
,四边形EFGH是矩形,
,
,
;
矩形EFGH的面积为
,
,其中
;
Ⅱ
由题意知,
,
令
,得
,
解得
,或
不合题意,舍去
;
令
,则
;
当
时,
,
单调递增;
当
时,
,
单调递减;
当
时,
取得最大值;
即
时,可使活动场地与停车场占地总面积最大.
【解析】【分析】
(
Ⅰ
)根据三角函数的定义及矩形的面积公式,即可确定函数的表达式;
(Ⅱ)
求导数,利用导数研究函数的单调性,即可求出函数的最值和此时的余弦值.
一、单选题(共11题)
1.在一幢20m高的楼顶,测得对面一塔吊顶的仰角为
,
塔基的俯角为
,
那么塔吊的高是(??)
A.??????????????B.??????????????C.??????????????D.?
2.已知两座灯塔A和B与海洋观察站C的距离都等于a
km,灯塔A在观察站C的北偏东20°,灯塔B在观察站C的南偏东40°,则灯塔A与B的距离为(?
)
A.?akm????????????????????????????????B.?akm
????????????????????????????????C.?akm????????????????????????????????D.?2akm
3.函数的部分图象如图,则(?
)
A.?????????????????B.?????????????????C.?????????????????D.?
4.水车在古代是进行灌溉引水的工具,是人类的一项古老的发明,也是人类利用自然和改造自然的象征.如图是一个半径为R的水车,一个水斗从点A(3
,﹣3)出发,沿圆周按逆时针方向匀速旋转,且旋转一周用时60秒.经过t秒后,水斗旋转到P点,设P的坐标为(x,y),其纵坐标满足y=f(t)=Rsin(ωt+φ)(t≥0,ω>0,|φ|<
).则下列叙述错误的是(??
)
A.???????????????????????????????????B.?当t∈[35,55]时,点P到x轴的距离的最大值为6
C.?当t∈[10,25]时,函数y=f(t)单调递减?????????D.?当t=20时,
5.已知
sinα+
cosα=2,则tanα=(
??)
A.?-
????????????????????????????????????B.?????????????????????????????????????C.?-
????????????????????????????????????D.?
6.设动直线x=a与函数f(x)=2sin2(
+x)和g(x)=
cos2x的图象分别交于M、N两点,则|MN|的最大值为(??
)
A.??????????????????????????????????????????B.??????????????????????????????????????????C.?2?????????????????????????????????????????D.?3
7.要测量底部不能到达的电视塔AB的高度,在C点测得塔顶A的仰角是45°,在D点测得塔顶A的仰角是30°,并测得水平面上的∠BCD=120°,CD=40m,则电视塔的高度为(?
)
A.?10
m???????????????????????????????B.?20m???????????????????????????????C.?20
m???????????????????????????????D.?40m
8.在一个港口,相邻两次高潮发生的时间相距12h,低潮时水深为9m,高潮时水深为15m.每天潮涨潮落时,该港口水的深度y(m)关于时间t(h)的函数图象可以近似地看成函数y=Asin(ωt+φ)+k的图象,其中0≤t≤24,且t=3时涨潮到一次高潮,则该函数的解析式可以是(??
)
A.??????????B.??????????C.??????????D.?
9.半径为1的球内切于一圆锥,则圆锥体积的最小值为( )
A.?2π???????????????????????????????????????B.????????????????????????????????????????C.?3π???????????????????????????????????????D.?
10.M,N是曲线y=πsinx与曲线y=πcosx的两个不同的交点,则|MN|的最小值为(?
)
A.?π?????????????????????????????????????B.??????????????????????????????????????C.??????????????????????????????????????D.?2π
11.矩形ABCD满足AB=2,AD=1,点A、B分别在射线OM,ON上,∠MON为直角,当C到点O的距离最大时,∠BAO的大小为( )
A.??????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?
二、填空题(共6题)
12.如图所示,PA,PB是⊙O的切线,AC是⊙O的直径,∠P=40°,则∠BAC=________.
13.某港口在一天24小时内的潮水的高度近似满足关系
,其中0≤t≤24,S的单位是m,t的单位是h,则18点时潮水起落的速度是________.
14.某城市一年中12个月的平均气温与月份的关系可近似地用三角函数
(x=1,2,3,…,12)来表示,已知6月份的月平均气温最高,为28℃,12月份的月平均气温最低,为18℃,则10月份的平均气温值为________℃
15.一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与灯塔S相距20海里,随后货轮继续沿正西方向航行30分钟到达N处后,又测得灯塔在货轮的北偏东45°,则货轮的速度为________海里/时.
16.某城市一年中12个月的平均气温与月份的关系可近似地用三角函数
来表示,已知6月份的月平均气温最高,为
,12月份的月平均气温最低,为
,则10月份的平均气温值为________
.
17.如图,一船自西向东匀速航行,上午10时到达一座灯塔P的南偏西75°距塔68海里的M处,下午2时到达这座灯塔的东南方向的N处,则这只船的航行速度为________?海里/小时.
三、综合(共3题)
18.如图,一个水轮的半径为4m,水轮圆心O距离水面2m,已知水轮每分钟转动5圈,如果当水轮上点P从水中浮现时(图中点p0)开始计算时间.
(1)将点p距离水面的高度z(m)表示为时间t(s)的函数;
(2)点p第一次到达最高点大约需要多少时间?
19.如图:已知圆O的直径是2,点C在直径AB的延长线上,BC=1,点P是圆O上的一个动点,以PC为边作正三角形PCD,且点D与圆心分别在PC的两侧,求四边形OPDC面积的最大值.
20.如图,AOB是一块半径为r的扇形空地,
.某单位计划在空地上修建一个矩形的活动场地OCDE及一矩形停车场EFGH,剩余的地方进行绿化.若
,设
(Ⅰ)记活动场地与停车场占地总面积为
,求
的表达式;
(Ⅱ)当
为何值时,可使活动场地与停车场占地总面积最大.
答案解析部分
一、单选题
1.【答案】
B
【解析】【解答】由题意,AB=20米,∠DAE=60°,∠DAC=45°,可知ABCD是正方形,有此易得CD=AD=20米,再由,∠DAE=60°,在直角三角形ADE中可求得DE=,
AD=20∴塔高为DE+CD="20+20"
=20(+1)故选B
【分析】本题考查已知三角函数模型的应用问题,解答本题的关键是建立起符合条件的模型,然后再由三角形中的相关知识进行运算,解三角形的应用一般是求距离(长度问题,高度问题等)解题时要注意综合利用所学的知识与题设中的条件,求解三角形的边与角
2.【答案】
B
【解析】解答:由图可知,∠ACB=120°,
由余弦定理
cos∠ACB=
=
=﹣
,
则AB=
a(km).
故选B.
分析:先根据题意确定∠ACB的值,再由余弦定理可直接求得|AB|的值.
3.【答案】
C
【解析】【解答】观察图象可知,A=1,T=4(3-1)=8,所以。将(1,1)代入得所以,
故选C。
4.【答案】C
【解析】【解答】解:由题意,R=
=6,T=60=
,∴ω=
,
点A(3
,﹣3)代入可得﹣3=6sinφ,∵|φ|<
),∴φ=﹣
.故A正确;
f(t)=6sin(
t﹣
),当t∈[35,55]时,
t﹣
∈[π,
],∴点P到x轴的距离的最大值为6,正确;
当t∈[10,25]时,
t﹣
∈[
π,
],函数y=f(t)单调递减,不正确;
当t=20时,
t﹣
=
,P的纵坐标为6,|PA|=
=6
,正确,
故选C.
【分析】求出函数的解析式,再分析选项,即可得出结论.
5.【答案】
D
【解析】【解答】解:∵
sinα+??cosα=2
,
∴
,
可得
,
∴
,
.
∴
,
则.
故答案为:D
【分析】sinα+??cosα=2
,
利用和差公式化简可得
,
即可求出的值。
6.【答案】
D
【解析】【解答】解:
,
=
.
故选D
【分析】利用二倍角公式先化简f(x),将|MN|表示成a的三角函数,利用公式
化简|MN|,利用三角函数的有界性求出最大值.
7.【答案】
D
【解析】解答:由题可设AB=x
,
则
,
在△DBC中,∠BCD=120°,CD=40,由余弦定理得BD2=BC2+CD2﹣2BC?CD?cos∠DCB
即:(
)2=(40)2+x2﹣2×40?x?cos120°
整理得:x2﹣20x﹣800=0
解得x=40或x=﹣20(舍)
所以,所求塔高为40米
.
故选D.
分析:设出AD=x
,
进而根据题意可表示出BD,DC,进而在△DBC中利用余弦定理建立方程求得x
.
8.【答案】A
【解析】【解答】解:依题意,
,解得
,
又T=
,
∴ω=
.
又f(3)=15,
∴3sin(
+φ)+12=15,
∴sin(
+φ)=1.
∴φ=0,
∴y=f(t)=3sin
t+12.
故选:A.
【分析】高潮时水深为A+K,低潮时水深为﹣A+K,联立方程组求得A和K的值,再由相邻两次高潮发生的时间相距12h,可知周期为12,由此求得ω值,再结合t=3时涨潮到一次高潮,把点(3,15)代入y=Asin(ωx+φ)+K的解析式求得φ,则函数y=f(t)的表达式可求.
9.【答案】
B
【解析】【解答】解:设母线与底面的夹角2α,底面半径R,内切球半径r=1,圆锥的高h
则:R=r?cotα=cotα,h=R?tan2α=cotα?tan2α=
,
圆锥的体积
=
,
而2α<90°,α<45°,所以:tanα<1,1﹣tan2α>0
又因为:tan2α+(1﹣tan2α)=1=定值
所以:当tan2α=1﹣tan2α,即tanα=时,V最小=
.
故选B.
【分析】设母线与底面的夹角2α,底面半径R,内切球半径r=1,圆锥的高h用α表示R,h,求出圆锥的体积V的表达式,利用基本不等式求出V最小
.
10.【答案】
C
【解析】解答:要求|MN|的最小值在,只要在一个周期内解即可
∵πsinx=πcosx
解得x=
或x=
得到两个点为(,
)和(
)
得到|MN|=
=
故选C
分析:|MN|的最小值即一个周期内两个交点的距离;列出方程求出两个交点坐标,据两点的距离公式求出|MN|的最小值.
11.【答案】
D
【解析】【解答】解:如图所示,
建立直角坐标系.
设∠OAB=θ,则∠CBE=θ.
.
B(0,2sinθ),C(sinθ,cosθ+2sinθ).
∴|OC|2=sin2θ+(cosθ+2sinθ)2
=1+4sinθcosθ+4sin2θ
=1+2sin2θ+2(1﹣cos2θ)
=+3,
∵
,
∴
.
∴当2
,
即时,|OC|2取得最大值,2+3.
故选:D.
【分析】如图所示,建立直角坐标系.设∠OAB=θ,则∠CBE=θ.
.
可得B(0,2sinθ),C(sinθ,cosθ+2sinθ).|OC|2=sin2θ+(cosθ+2sinθ)2
=+3,由于
,
可得
.
即可得出.
二、填空题
12.【答案】
20°
【解析】【解答】连接OP,
根据切线的性质可知,AP=BP,∠DAP=∠DPB=
∠P=
×40°=20°,
在△ADP与△BPD中,AP=BP,DP=DP,∠DAP=∠DPB=20°,
∴△ADP≌△BPD,OP⊥AB,
∴∠DAP=90°﹣∠DAP=90°﹣20°=70°,
∵AP是⊙O的切线,AC是直径,
∴∠OAP=90°,
∴∠BAC=∠OAP﹣∠DAP=90°﹣70°=20°.
【分析】连接OP,根据切线的性质可求出△ADP≌△BPD及∠APD的度数,根据直角三角形的性质可求出∠DAP的度数,由切线的性质定理解答即可.
13.【答案】
【解析】【解答】由题意,∵
∴v=S'=
当t=18时,速度v=
故答案为
【分析】利用导数的物理意义,高度对时间的导数,从而得解.
14.【答案】
16
【解析】【解答】据题意得28=a+A,
=a﹣A
解得a=20,A=8
所以
令x=10得y=
=16
故答案为:16
【分析】根据题意列出方程组,求出a,A,求出年中12个月的平均气温与月份的关系可近似地用三角函数;将x=10代入求出10月份的平均气温值.
15.【答案】
【解析】【解答】由题意,如图所示,
可知∠SMN=15°+90°=105°,∠SNM=45°,SM=20,∴∠NSM=30°,
在△SMN中,由正弦定理可得:
,
即
,解得:MN=
,
∴货轮的速度为
=
海里/时.
故答案为:
.
【分析】由题意可知,在△SMN中,由正弦定理可得MN=
,
即可得出货轮的速度.
16.【答案】
20.5
【解析】【解答】根据题意,由于一年中12个月的平均气温与月份x的关系可近似地用三角函数y=a+Acos[
(x-6)](x=1,2,3,…,12),由于x=6,y=28,可知a+A=28,x=12,a-A=18,得到a=23,A=5,当x=10,y=20.5,故可知则10月份的平均气温值为20.5℃。
【分析】根据实际问题的已知条件结合三角型函数图象与a和A的关系,从而建立关于a和A的方程组,进而求出a和A的值,从而求出三角型函数的解析式,再利用三角型函数的解析式求出10月份的平均气温值。
17.【答案】
【解析】【解答】解:由题意知∠MPN=75°+45°=120°,∠PNM=45°.
在△PMN中,由正弦定理,得
,
∴MN=
又由M到N所用时间为14﹣10=4(小时),
∴船的航行速度v==(海里/时);
故答案为:
.
【分析】根据题意可求得∠MPN和,∠PNM进而利用正弦定理求得MN的值,进而求得船航行的时间,最后利用里程除以时间即可求得问题的答案.
三、综合题
18.【答案】
(1)解:依题意可知z的最大值为6,最小为﹣2,
∴
?
;
∵op每秒钟内所转过的角为
,得z=4sin
,
当t=0时,z=0,得sinφ=﹣
,即φ=﹣
,故所求的函数关系式为
z=4sin
+2
(2)解:令z=4sin
+2=6,得sin
=1,
取
,得t=4,
故点P第一次到达最高点大约需要4S
【解析】【分析】(1)先根据z的最大和最小值求得A和B,利用周期求得ω,当x=0时,z=0,进而求得φ的值,则函数的表达式可得;(2)令最大值为6,即
z=4sin
+2=6可求得时间.
19.【答案】
解:设∠POB=θ.在△POC中,由余弦定理得:PC2=OP2+OC2﹣2OP?OC?cosθ=5﹣4cosθ
所以
,
当时,即时,
四边形OPDC面积的最大值为
2+
.
【解析】【分析】设∠POB=θ,将面积表示为角的函数,再利用三角函数求最值的方法求最值.
20.【答案】
解:
Ⅰ
由题意得,在矩形OCDE中,
,
,
,
矩形OCDE的面积为
;
又
,四边形EFGH是矩形,
,
,
;
矩形EFGH的面积为
,
,其中
;
Ⅱ
由题意知,
,
令
,得
,
解得
,或
不合题意,舍去
;
令
,则
;
当
时,
,
单调递增;
当
时,
,
单调递减;
当
时,
取得最大值;
即
时,可使活动场地与停车场占地总面积最大.
【解析】【分析】
(
Ⅰ
)根据三角函数的定义及矩形的面积公式,即可确定函数的表达式;
(Ⅱ)
求导数,利用导数研究函数的单调性,即可求出函数的最值和此时的余弦值.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
