5.1相交线课后练习2020-2021学年华东师大版七年级上册数学 (Word版 含答案)
文档属性
| 名称 | 5.1相交线课后练习2020-2021学年华东师大版七年级上册数学 (Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 229.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-30 23:10:08 | ||
图片预览


文档简介
第五章相交线与平行线5.1相交线课后练习2020-2021学年上学期七年级上册初中数学华师大版
一、单选题(共12题
)
1.如图所示,三角形ABC中,∠BAC=90°,过点A画AD⊥BC。则下列说法不正确的是(
???)
A.?线段AD是点A与直线BC上各点连接的所有线段中最短的
B.?线段AB是点B到直线AD的垂线段
C.?点A到直线BC的距离是线段AD的长
D.?点C到直线AB的距离是线段AC的长
2.如图,某单位要在河岸l上建一个水泵房引水到C处,他们的做法是:过点C作CD⊥l于点D,将水泵房建在了D处.这样做最节省水管长度,其数学道理是(?
)
A.?两点之间,线段最短????????????????????????????B.?在同一平面内,过一点有且只有一条直线与已知直线垂直
C.?两点确定一条直线????????????????????????????????D.?直线外一点与直线上所有点的连线中,垂线段最短
3.如图,点
是直线
外一点,
,
,
,
都在直线上,
于
,下列线段最短的是(?
)
A.???????????????????????????????????????B.???????????????????????????????????????C.???????????????????????????????????????D.?
4.如图,
和
都是直角,如果
,那么
等于(??
)
A.?40°???????????????????????????????????????B.?30°???????????????????????????????????????C.?50°???????????????????????????????????????D.?60°
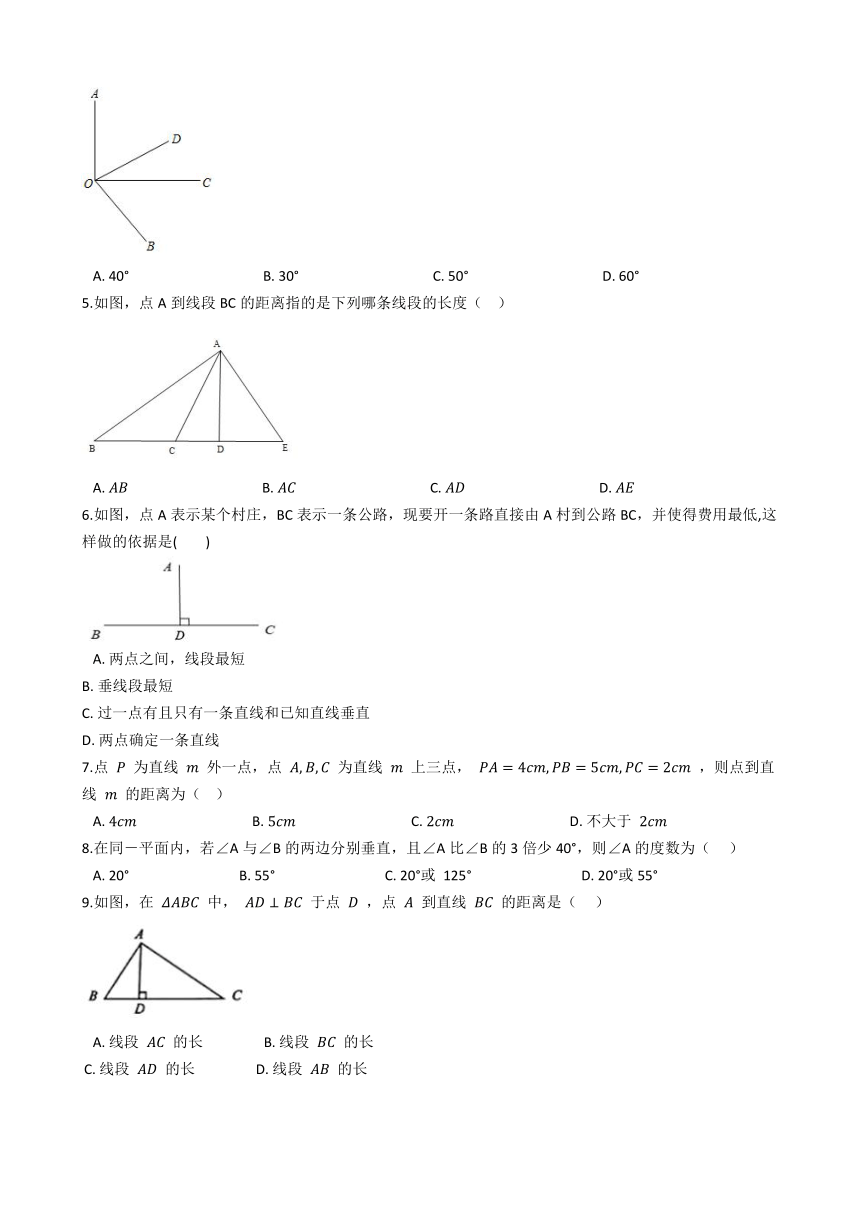
5.如图,点A到线段BC的距离指的是下列哪条线段的长度(??
)
A.????????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
6.如图,点A表示某个村庄,BC表示一条公路,现要开一条路直接由A村到公路BC,并使得费用最低,这样做的依据是(??????
)
A.?两点之间,线段最短
B.?垂线段最短
C.?过一点有且只有一条直线和已知直线垂直
D.?两点确定一条直线
7.点
为直线
外一点,点
为直线
上三点,
,则点到直线
的距离为(??
)
A.??????????????????????????????????B.??????????????????????????????????C.??????????????????????????????????D.?不大于
8.在同-平面内,若∠A与∠B的两边分别垂直,且∠A比∠B的3倍少40°,则∠A的度数为(???
)
A.?20°????????????????????????????????B.?55°????????????????????????????????C.?20°或
125°????????????????????????????????D.?20°或55°
9.如图,在
中,
于点
,点
到直线
的距离是(???
)
A.?线段
的长?????????????????B.?线段
的长
C.?线段
的长?????????????????D.?线段
的长
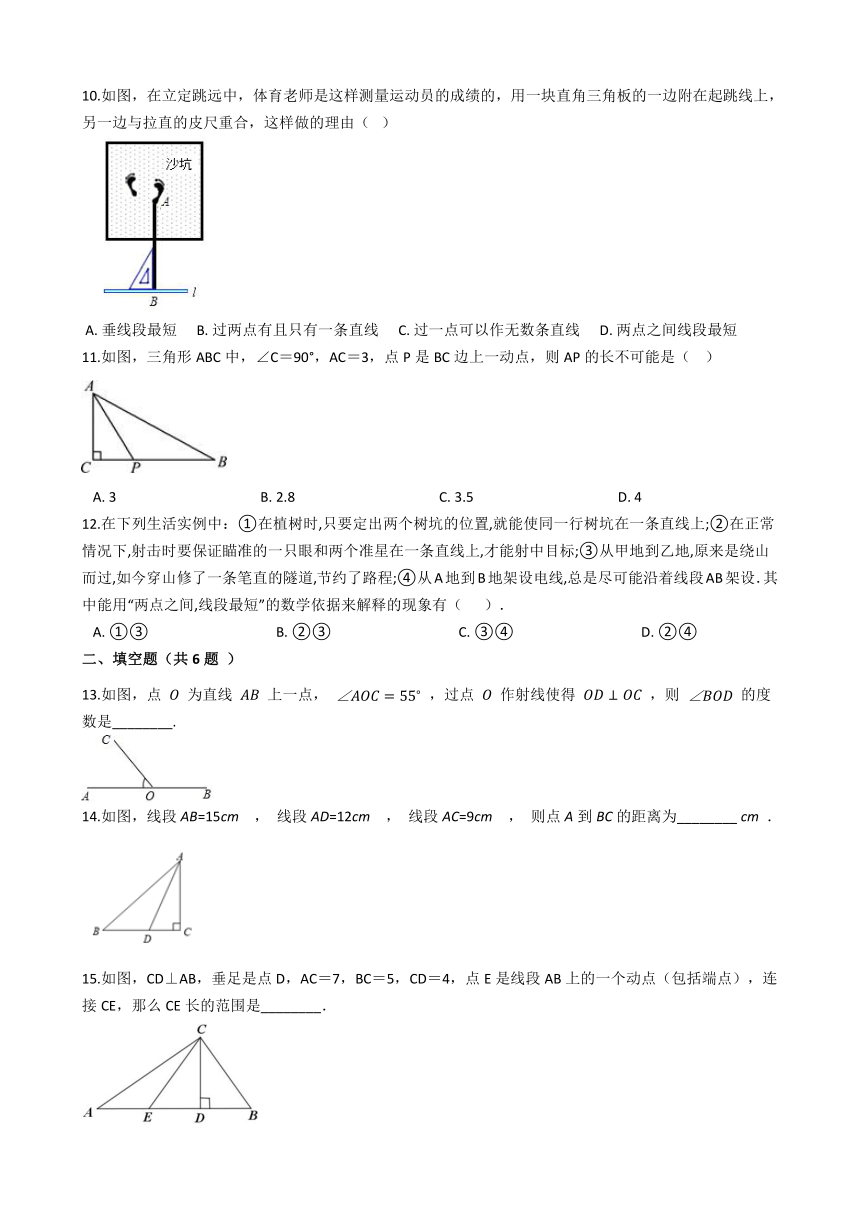
10.如图,在立定跳远中,体育老师是这样测量运动员的成绩的,用一块直角三角板的一边附在起跳线上,另一边与拉直的皮尺重合,这样做的理由(?
)
?A.?垂线段最短?????B.?过两点有且只有一条直线?????C.?过一点可以作无数条直线?????D.?两点之间线段最短
11.如图,三角形ABC中,∠C=90°,AC=3,点P是BC边上一动点,则AP的长不可能是(??
)
A.?3??????????????????????????????????????????B.?2.8??????????????????????????????????????????C.?3.5??????????????????????????????????????????D.?4
12.在下列生活实例中:①在植树时,只要定出两个树坑的位置,就能使同一行树坑在一条直线上;②在正常情况下,射击时要保证瞄准的一只眼和两个准星在一条直线上,才能射中目标;③从甲地到乙地,原来是绕山而过,如今穿山修了一条笔直的隧道,节约了路程;④从A地到B地架设电线,总是尽可能沿着线段AB架设.其中能用“两点之间,线段最短”的数学依据来解释的现象有(????
).
A.?①③?????????????????????????????????????B.?②③?????????????????????????????????????C.?③④?????????????????????????????????????D.?②④
二、填空题(共6题
)
13.如图,点
为直线
上一点,
,过点
作射线使得
,则
的度数是________.
14.如图,线段AB=15cm
,
线段AD=12cm
,
线段AC=9cm
,
则点A到BC的距离为________
cm
.
15.如图,CD⊥AB,垂足是点D,AC=7,BC=5,CD=4,点E是线段AB上的一个动点(包括端点),连接CE,那么CE长的范围是________.
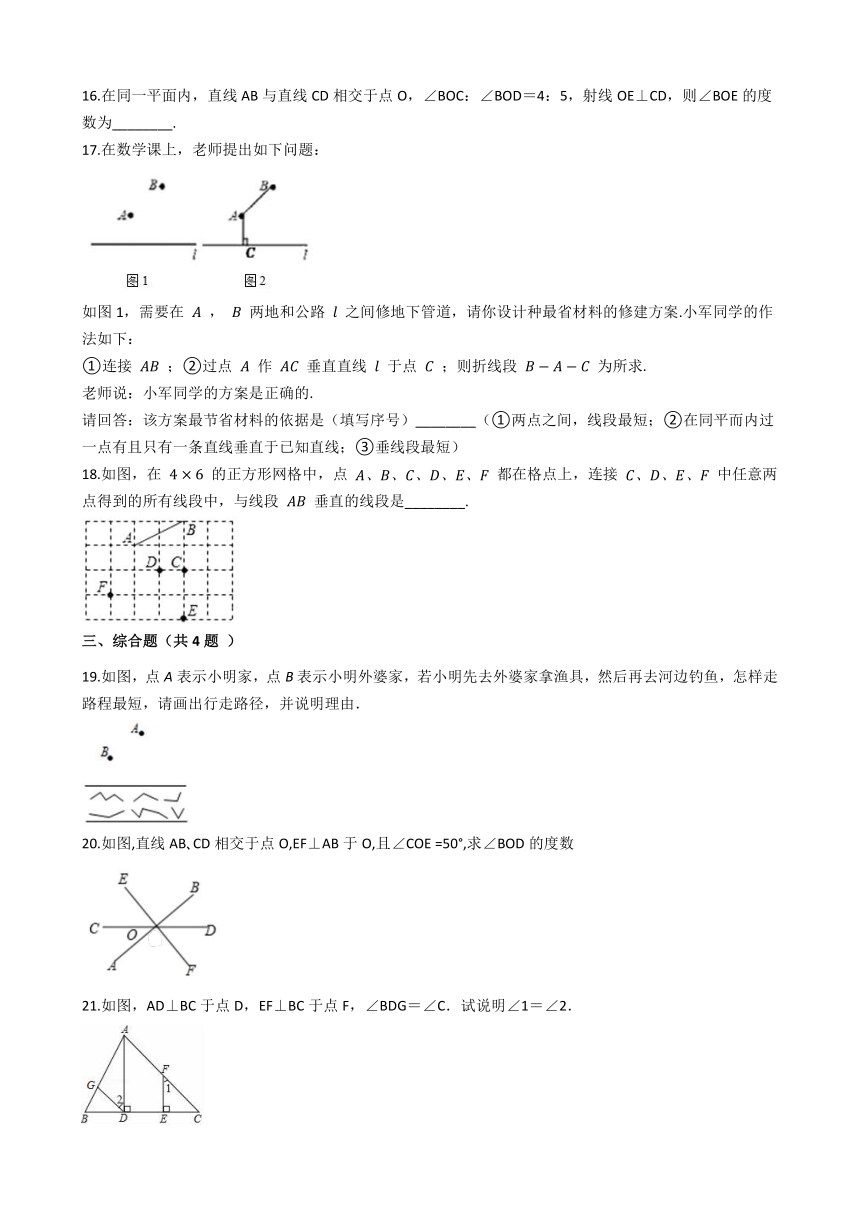
16.在同一平面内,直线AB与直线CD相交于点O,∠BOC:∠BOD=4:5,射线OE⊥CD,则∠BOE的度数为________.
17.在数学课上,老师提出如下问题:
如图1,需要在
,
两地和公路
之间修地下管道,请你设计种最省材料的修建方案.小军同学的作法如下:
①连接
;②过点
作
垂直直线
于点
;则折线段
为所求.
老师说:小军同学的方案是正确的.
请回答:该方案最节省材料的依据是(填写序号)________(①两点之间,线段最短;②在同平而内过一点有且只有一条直线垂直于已知直线;③垂线段最短)
18.如图,在
的正方形网格中,点
都在格点上,连接
中任意两点得到的所有线段中,与线段
垂直的线段是________.
三、综合题(共4题
)
19.如图,点A表示小明家,点B表示小明外婆家,若小明先去外婆家拿渔具,然后再去河边钓鱼,怎样走路程最短,请画出行走路径,并说明理由.
20.如图,直线AB?CD相交于点O,EF⊥AB于O,且∠COE
=50°,求∠BOD的度数
21.如图,AD⊥BC于点D,EF⊥BC于点F,∠BDG=∠C.试说明∠1=∠2.
22.如图,AC⊥BC于C,CD⊥AB于D,DE⊥BC于E,试比较四条线段DE、DC、AC、AB的大小.
答案解析部分
一、单选题
1.【答案】
B
【解析】【解答】解:A:线段AD是点A与直线BC上各点连接的所有线段中最短的,故正确,不符合题意;
B:线段AB是点B到直线AC的垂线段,故错误,符合题意;
C:点A到直线BC的距离是线段AD的长,故正确,不符合题意;
D:点C到直线AB的距离是线段AC的长,故正确,不符合题意.
故答案为:B.
【分析】根据垂线段最短可判断A的正误;根据点到直线的距离的概念可判断B、C、D的正误.
2.【答案】
D
【解析】【解答】解:因为CD⊥l于点D,根据垂线段最短,所以CD为C点到河岸l的最短路径.
故答案为:D.
【分析】利用垂线段最短的性质求解即可。
3.【答案】
C
【解析】【解答】因为点
是直线
a
外一点,
A
,
B
,
C
,
D
都在直线上,
于
,
所以,根据垂线段的性质可知:线段
PB
最短.
故答案为:C.
【分析】根据垂线段最短进行作答求解即可。
4.【答案】
B
【解析】【解答】解:∵∠BOD是直角,
∴∠BOD=90°,
∵∠AOB=150°,
∴∠AOD=∠AOB-∠BOD=60°,
又∵∠AOC是直角,
∴∠AOC=90°,
∴∠COD=∠AOC-∠AOD=30°.
故答案为:B.
【分析】由于∠BOD、∠AOC是直角,可得∠BOD=∠AOC=90°,先求出∠AOD=∠AOB-∠BOD=60°,继而求出∠COD=∠AOC-∠AOD=30°.
5.【答案】
C
【解析】【解答】解:由图可得,AD⊥BC于D,点A到线段BC的距离指线段AD的长,
故答案为:C.
【分析】根据点到直线的距离的定义求解即可。
6.【答案】
B
【解析】【解答】解:∵从直线外一点到这条直线上各点所连线段中,垂线段最短,
∴过点A作AD⊥BC于点D,这样做的理由是垂线段最短.
故答案为:B.
【分析】根据垂线段最短进行判断求解即可。
7.【答案】
D
【解析】【解答】解:当PC⊥m时,PC是点P到直线m的距离,即点P到直线m的距离2cm,
当PC不垂直直线m时,点P到直线m的距离小于PC的长,即点P到直线m的距离小于2cm,
综上所述:点P到直线m的距离不大于2cm,
故答案为:D.
【分析】根据点到直线的距离是直线外的点与直线上垂足间的线段的长,再根据垂线段最短,可得答案.
8.【答案】
C
【解析】【解答】解:设∠B是x度,根据题意,得
①两个角相等时,如图1:
∠B=∠A=x°,
x=3x-40
解得,x=20,
故∠A=20°,
②两个角互补时,如图2:
x+3x-40=180,
所以x=55,
3×55°-40°=125°
故∠A的度数为:20°或125°.
故答案为:C.
【分析】因为两个角的两边分别垂直,则这两个角相等或互补,又因∠A比∠B的3倍少40°,所以它们互补,可设∠B是x度,利用方程即可解决问题.
9.【答案】
C
【解析】【解答】解:因为
于点
,所以AD的长即为点A到直线BC的距离;
故答案为:C.
【分析】根据点到直线的距离的定义进行判断求解即可。
10.【答案】
A
【解析】【解答】解:这样做的理由是根据垂线段最短.
故答案为:A.
【分析】根据垂线段的性质:垂线段最短进行解答即可.
11.【答案】
B
【解析】【解答】解:∵∠C=90°,点P是BC边上一动点,
∴AP>AC,
∵AC=3,
∴AP>3,
∴AP的长不可能是2.8.
故答案为:B.
【分析】根据垂线段最短判断出AP>AC,然后选择答案即可.
12.【答案】
C
【解析】【解答】解:①在植树时,只要定出两个树坑的位置,就能使同一行树坑在一条直线上,依据的是两点确定一条直线;
②在正常情况下,射击时要保证瞄准的一只眼和两个准星在一条直线上,才能射中目标,依据的是两点确定一条直线;
③从甲地到乙地,原来是绕山而过,如今穿山修了一条笔直的隧道,节约了路程,依据的是两点之间线段最短;
④从A地到B地架设电线,总是尽可能沿着线段AB架设,依据的是两点之间线段最短;
∴能用“两点之间,线段最短”的数学依据来解释的现象有:③④;
故答案为:C.
【分析】根据垂线段最短、直线和线段的性质即可得到结论.
二、填空题
13.【答案】
或
【解析】【解答】如图所示:
有两种情况.
①
②
故
=
或
.
【分析】
有两种情况.①如图1,OC与OD在直线AB的同侧时,②如图2,OC与OD在直线AB的两侧时,根据垂直的定义及角的计算分别解答即可.
14.【答案】
9
【解析】【解答】解:如图所示,已知
,AC=9cm
,
由点到直线的距离定义可知,点A到BC的距离为AC的长度,即为9cm;
故答案为:9.
【分析】从直线外一点到这条直线所画的垂直线段最短,它的长度叫做点到直线的距离,如图中,AC的距离就是点A到直线BC的距离.
15.【答案】
4≤CE≤7
【解析】【解答】解:∵CD⊥AB,垂足是点D,AC=7,BC=5,CD=4,
∴CE长的范围是4≤CE≤7,
故答案为:4≤CE≤7.
【分析】根据垂线段最短解答即可.
16.【答案】
170°或10°
【解析】【解答】∵∠BOC:∠BOD=4:5,
∵∠BOC=
×180°=80°,
①如图1,OE在AB的上方时,
又∵OE⊥CD,
∴∠COE=90°
,
∴∠BOE=90°
+80°
=170°
②如图2,OE在AB的下方时,
同理得∠BOE=90°
﹣80°=10°,
综上,∠BOE的度数为170
°或10°.
故答案是:170°或10°
.
【分析】首先根据叙述作出图形,根据条件求得∠COB的度数,分两种情况根据角的和与差即可求解.
17.【答案】
①③
【解析】【解答】解:由于两点之间距离最短,故连接AB,
由于垂线段最短可知,过点A作AC⊥直线l于点C,此时AC最短,
故答案为:①③.
【分析】根据线段公理“两点之间距离最短”和垂线的性质“垂线段最短”可求解.
18.【答案】
DE
【解析】【解答】解:画出C、D、E、F中任意两点所在直线,如图所示,则与线段
垂直的线段是DE,
故答案为:DE.
【分析】分别画出C、D、E、F中任意两点所在直线,结合图形根据垂直的定义即可求解.
三、解答题
19.【答案】
解:如图,连接AB(两点间线段最短),过B作BC垂直于河岸(垂线段最短),
【解析】【分析】根据两点间线段最短和垂线段最短画图解答即可.
20.【答案】
解:∵EF⊥AB
∴∠EOB=90°
∵∠COE
=50°
∴∠BOD=180°-∠COE-∠EOB=40°
【解析】【分析】根据垂直的定义可得∠EOB=90°,然后根据平角的定义即可求出结论.
21.【答案】
证明:∵AD⊥BC于点D,EF⊥BC于点F,∴∠ADB=∠FEC=90°.
∵∠BDG=∠C,∠2+∠BDG=90°,∠1+∠C=90°,∴∠1=∠2.
【解析】【分析】根据垂直的定义及互余的性质解答即可.
22.【答案】
解:∵AC⊥BC,
∴AC<AB,
∵CD⊥AB,
∴DC<AC,
∵DE⊥BC,
∴DE<DC,
∴DE<DC<AC<AB
【解析】【分析】分别根据垂线段最短依次进行判断,然后按照从小到大的顺序排列即可.
一、单选题(共12题
)
1.如图所示,三角形ABC中,∠BAC=90°,过点A画AD⊥BC。则下列说法不正确的是(
???)
A.?线段AD是点A与直线BC上各点连接的所有线段中最短的
B.?线段AB是点B到直线AD的垂线段
C.?点A到直线BC的距离是线段AD的长
D.?点C到直线AB的距离是线段AC的长
2.如图,某单位要在河岸l上建一个水泵房引水到C处,他们的做法是:过点C作CD⊥l于点D,将水泵房建在了D处.这样做最节省水管长度,其数学道理是(?
)
A.?两点之间,线段最短????????????????????????????B.?在同一平面内,过一点有且只有一条直线与已知直线垂直
C.?两点确定一条直线????????????????????????????????D.?直线外一点与直线上所有点的连线中,垂线段最短
3.如图,点
是直线
外一点,
,
,
,
都在直线上,
于
,下列线段最短的是(?
)
A.???????????????????????????????????????B.???????????????????????????????????????C.???????????????????????????????????????D.?
4.如图,
和
都是直角,如果
,那么
等于(??
)
A.?40°???????????????????????????????????????B.?30°???????????????????????????????????????C.?50°???????????????????????????????????????D.?60°
5.如图,点A到线段BC的距离指的是下列哪条线段的长度(??
)
A.????????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
6.如图,点A表示某个村庄,BC表示一条公路,现要开一条路直接由A村到公路BC,并使得费用最低,这样做的依据是(??????
)
A.?两点之间,线段最短
B.?垂线段最短
C.?过一点有且只有一条直线和已知直线垂直
D.?两点确定一条直线
7.点
为直线
外一点,点
为直线
上三点,
,则点到直线
的距离为(??
)
A.??????????????????????????????????B.??????????????????????????????????C.??????????????????????????????????D.?不大于
8.在同-平面内,若∠A与∠B的两边分别垂直,且∠A比∠B的3倍少40°,则∠A的度数为(???
)
A.?20°????????????????????????????????B.?55°????????????????????????????????C.?20°或
125°????????????????????????????????D.?20°或55°
9.如图,在
中,
于点
,点
到直线
的距离是(???
)
A.?线段
的长?????????????????B.?线段
的长
C.?线段
的长?????????????????D.?线段
的长
10.如图,在立定跳远中,体育老师是这样测量运动员的成绩的,用一块直角三角板的一边附在起跳线上,另一边与拉直的皮尺重合,这样做的理由(?
)
?A.?垂线段最短?????B.?过两点有且只有一条直线?????C.?过一点可以作无数条直线?????D.?两点之间线段最短
11.如图,三角形ABC中,∠C=90°,AC=3,点P是BC边上一动点,则AP的长不可能是(??
)
A.?3??????????????????????????????????????????B.?2.8??????????????????????????????????????????C.?3.5??????????????????????????????????????????D.?4
12.在下列生活实例中:①在植树时,只要定出两个树坑的位置,就能使同一行树坑在一条直线上;②在正常情况下,射击时要保证瞄准的一只眼和两个准星在一条直线上,才能射中目标;③从甲地到乙地,原来是绕山而过,如今穿山修了一条笔直的隧道,节约了路程;④从A地到B地架设电线,总是尽可能沿着线段AB架设.其中能用“两点之间,线段最短”的数学依据来解释的现象有(????
).
A.?①③?????????????????????????????????????B.?②③?????????????????????????????????????C.?③④?????????????????????????????????????D.?②④
二、填空题(共6题
)
13.如图,点
为直线
上一点,
,过点
作射线使得
,则
的度数是________.
14.如图,线段AB=15cm
,
线段AD=12cm
,
线段AC=9cm
,
则点A到BC的距离为________
cm
.
15.如图,CD⊥AB,垂足是点D,AC=7,BC=5,CD=4,点E是线段AB上的一个动点(包括端点),连接CE,那么CE长的范围是________.
16.在同一平面内,直线AB与直线CD相交于点O,∠BOC:∠BOD=4:5,射线OE⊥CD,则∠BOE的度数为________.
17.在数学课上,老师提出如下问题:
如图1,需要在
,
两地和公路
之间修地下管道,请你设计种最省材料的修建方案.小军同学的作法如下:
①连接
;②过点
作
垂直直线
于点
;则折线段
为所求.
老师说:小军同学的方案是正确的.
请回答:该方案最节省材料的依据是(填写序号)________(①两点之间,线段最短;②在同平而内过一点有且只有一条直线垂直于已知直线;③垂线段最短)
18.如图,在
的正方形网格中,点
都在格点上,连接
中任意两点得到的所有线段中,与线段
垂直的线段是________.
三、综合题(共4题
)
19.如图,点A表示小明家,点B表示小明外婆家,若小明先去外婆家拿渔具,然后再去河边钓鱼,怎样走路程最短,请画出行走路径,并说明理由.
20.如图,直线AB?CD相交于点O,EF⊥AB于O,且∠COE
=50°,求∠BOD的度数
21.如图,AD⊥BC于点D,EF⊥BC于点F,∠BDG=∠C.试说明∠1=∠2.
22.如图,AC⊥BC于C,CD⊥AB于D,DE⊥BC于E,试比较四条线段DE、DC、AC、AB的大小.
答案解析部分
一、单选题
1.【答案】
B
【解析】【解答】解:A:线段AD是点A与直线BC上各点连接的所有线段中最短的,故正确,不符合题意;
B:线段AB是点B到直线AC的垂线段,故错误,符合题意;
C:点A到直线BC的距离是线段AD的长,故正确,不符合题意;
D:点C到直线AB的距离是线段AC的长,故正确,不符合题意.
故答案为:B.
【分析】根据垂线段最短可判断A的正误;根据点到直线的距离的概念可判断B、C、D的正误.
2.【答案】
D
【解析】【解答】解:因为CD⊥l于点D,根据垂线段最短,所以CD为C点到河岸l的最短路径.
故答案为:D.
【分析】利用垂线段最短的性质求解即可。
3.【答案】
C
【解析】【解答】因为点
是直线
a
外一点,
A
,
B
,
C
,
D
都在直线上,
于
,
所以,根据垂线段的性质可知:线段
PB
最短.
故答案为:C.
【分析】根据垂线段最短进行作答求解即可。
4.【答案】
B
【解析】【解答】解:∵∠BOD是直角,
∴∠BOD=90°,
∵∠AOB=150°,
∴∠AOD=∠AOB-∠BOD=60°,
又∵∠AOC是直角,
∴∠AOC=90°,
∴∠COD=∠AOC-∠AOD=30°.
故答案为:B.
【分析】由于∠BOD、∠AOC是直角,可得∠BOD=∠AOC=90°,先求出∠AOD=∠AOB-∠BOD=60°,继而求出∠COD=∠AOC-∠AOD=30°.
5.【答案】
C
【解析】【解答】解:由图可得,AD⊥BC于D,点A到线段BC的距离指线段AD的长,
故答案为:C.
【分析】根据点到直线的距离的定义求解即可。
6.【答案】
B
【解析】【解答】解:∵从直线外一点到这条直线上各点所连线段中,垂线段最短,
∴过点A作AD⊥BC于点D,这样做的理由是垂线段最短.
故答案为:B.
【分析】根据垂线段最短进行判断求解即可。
7.【答案】
D
【解析】【解答】解:当PC⊥m时,PC是点P到直线m的距离,即点P到直线m的距离2cm,
当PC不垂直直线m时,点P到直线m的距离小于PC的长,即点P到直线m的距离小于2cm,
综上所述:点P到直线m的距离不大于2cm,
故答案为:D.
【分析】根据点到直线的距离是直线外的点与直线上垂足间的线段的长,再根据垂线段最短,可得答案.
8.【答案】
C
【解析】【解答】解:设∠B是x度,根据题意,得
①两个角相等时,如图1:
∠B=∠A=x°,
x=3x-40
解得,x=20,
故∠A=20°,
②两个角互补时,如图2:
x+3x-40=180,
所以x=55,
3×55°-40°=125°
故∠A的度数为:20°或125°.
故答案为:C.
【分析】因为两个角的两边分别垂直,则这两个角相等或互补,又因∠A比∠B的3倍少40°,所以它们互补,可设∠B是x度,利用方程即可解决问题.
9.【答案】
C
【解析】【解答】解:因为
于点
,所以AD的长即为点A到直线BC的距离;
故答案为:C.
【分析】根据点到直线的距离的定义进行判断求解即可。
10.【答案】
A
【解析】【解答】解:这样做的理由是根据垂线段最短.
故答案为:A.
【分析】根据垂线段的性质:垂线段最短进行解答即可.
11.【答案】
B
【解析】【解答】解:∵∠C=90°,点P是BC边上一动点,
∴AP>AC,
∵AC=3,
∴AP>3,
∴AP的长不可能是2.8.
故答案为:B.
【分析】根据垂线段最短判断出AP>AC,然后选择答案即可.
12.【答案】
C
【解析】【解答】解:①在植树时,只要定出两个树坑的位置,就能使同一行树坑在一条直线上,依据的是两点确定一条直线;
②在正常情况下,射击时要保证瞄准的一只眼和两个准星在一条直线上,才能射中目标,依据的是两点确定一条直线;
③从甲地到乙地,原来是绕山而过,如今穿山修了一条笔直的隧道,节约了路程,依据的是两点之间线段最短;
④从A地到B地架设电线,总是尽可能沿着线段AB架设,依据的是两点之间线段最短;
∴能用“两点之间,线段最短”的数学依据来解释的现象有:③④;
故答案为:C.
【分析】根据垂线段最短、直线和线段的性质即可得到结论.
二、填空题
13.【答案】
或
【解析】【解答】如图所示:
有两种情况.
①
②
故
=
或
.
【分析】
有两种情况.①如图1,OC与OD在直线AB的同侧时,②如图2,OC与OD在直线AB的两侧时,根据垂直的定义及角的计算分别解答即可.
14.【答案】
9
【解析】【解答】解:如图所示,已知
,AC=9cm
,
由点到直线的距离定义可知,点A到BC的距离为AC的长度,即为9cm;
故答案为:9.
【分析】从直线外一点到这条直线所画的垂直线段最短,它的长度叫做点到直线的距离,如图中,AC的距离就是点A到直线BC的距离.
15.【答案】
4≤CE≤7
【解析】【解答】解:∵CD⊥AB,垂足是点D,AC=7,BC=5,CD=4,
∴CE长的范围是4≤CE≤7,
故答案为:4≤CE≤7.
【分析】根据垂线段最短解答即可.
16.【答案】
170°或10°
【解析】【解答】∵∠BOC:∠BOD=4:5,
∵∠BOC=
×180°=80°,
①如图1,OE在AB的上方时,
又∵OE⊥CD,
∴∠COE=90°
,
∴∠BOE=90°
+80°
=170°
②如图2,OE在AB的下方时,
同理得∠BOE=90°
﹣80°=10°,
综上,∠BOE的度数为170
°或10°.
故答案是:170°或10°
.
【分析】首先根据叙述作出图形,根据条件求得∠COB的度数,分两种情况根据角的和与差即可求解.
17.【答案】
①③
【解析】【解答】解:由于两点之间距离最短,故连接AB,
由于垂线段最短可知,过点A作AC⊥直线l于点C,此时AC最短,
故答案为:①③.
【分析】根据线段公理“两点之间距离最短”和垂线的性质“垂线段最短”可求解.
18.【答案】
DE
【解析】【解答】解:画出C、D、E、F中任意两点所在直线,如图所示,则与线段
垂直的线段是DE,
故答案为:DE.
【分析】分别画出C、D、E、F中任意两点所在直线,结合图形根据垂直的定义即可求解.
三、解答题
19.【答案】
解:如图,连接AB(两点间线段最短),过B作BC垂直于河岸(垂线段最短),
【解析】【分析】根据两点间线段最短和垂线段最短画图解答即可.
20.【答案】
解:∵EF⊥AB
∴∠EOB=90°
∵∠COE
=50°
∴∠BOD=180°-∠COE-∠EOB=40°
【解析】【分析】根据垂直的定义可得∠EOB=90°,然后根据平角的定义即可求出结论.
21.【答案】
证明:∵AD⊥BC于点D,EF⊥BC于点F,∴∠ADB=∠FEC=90°.
∵∠BDG=∠C,∠2+∠BDG=90°,∠1+∠C=90°,∴∠1=∠2.
【解析】【分析】根据垂直的定义及互余的性质解答即可.
22.【答案】
解:∵AC⊥BC,
∴AC<AB,
∵CD⊥AB,
∴DC<AC,
∵DE⊥BC,
∴DE<DC,
∴DE<DC<AC<AB
【解析】【分析】分别根据垂线段最短依次进行判断,然后按照从小到大的顺序排列即可.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
