14.1勾股定理课后练习2020-2021学年华东师大版 八年级上册(Word版 含答案)
文档属性
| 名称 | 14.1勾股定理课后练习2020-2021学年华东师大版 八年级上册(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 158.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-30 00:00:00 | ||
图片预览




文档简介
第十四章勾股定理14.1勾股定理课后练习2020-2021学年上学期八年级上册初中数学华东师大版
一、单选题(共12题)
1.如图,在
的正方形网格图中,小正方形的边长为1,
的顶点均在格点上,则下列关于
的说法错误的是(??
)
A.?是直角三角形??????????????????B.?tam
??????????????????C.?面积为
??????????????????D.?
边上的高为
2.已知三角形的三边长之比为1:1:
,则此三角形一定是(??
)
A.?锐角三角形????????????????????B.?钝角三角形????????????????????C.?等边三角形????????????????????D.?等腰直角三角形
3.下列各组数中,能构成直角三角形的是(??
)
A.?3,4,6?????????????????????????B.?1,1,
?????????????????????????C.?6,8,11?????????????????????????D.?5,12,23
4.在
中,
,
,
,则
的长为(???
)
A.?1??????????????????????????????????????B.?2??????????????????????????????????????C.?
或4??????????????????????????????????????D.?2或4
5.在下列由线段a,b,c的长为三边的三角形中,不能构成直角三角形的是(??
)
A.?a=4,b=5,c=6
B.?a=12,b=5,c=13
C.?a=6,b=8,c=10
D.?a=7,b=24,c=25
6.一个直角三角形的两条直角边的和是14cm,面积是24cm2
,
则其斜边长为(?
)
A.?2
cm???????????????????????????????B.?10cm???????????????????????????????C.?8cm???????????????????????????????D.?4
cm
7.如图,在
中,
是
的角平分线,
于点
,
,
,
,则
长是(??
)
A.?1?????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?2
8.将一个长为2,宽为1的长方形ABCD按如图方式放在数轴上,使点A与原点O重合,若以O为圆心,以AC的长为半径画圆,则这个圆与数轴的交点所表示的数是(
?)
A.?????????????????????????????????????B.?﹣
????????????????????????????????????C.?±
????????????????????????????????????D.?±2.5
9.下列几组数中,不能作为直角三角形三边长度的是(??
)
A.?1.5,2,2.5??????????????????????B.?5,12,14??????????????????????C.?30,40,50??????????????????????D.?1,2,
10.已知a、b、c为
的三边,且满足
,则
是(??
)
A.?等腰三角形?????????????B.?直角三角形?????????????C.?等腰直角三角形?????????????D.?等腰三角形或直角三角形
11.在
中,已知
,AD是
的角平分线,
于点E.若
的面积为S,则
的面积为(??
)
A.??????????????????????????????????????B.??????????????????????????????????????C.??????????????????????????????????????D.?
12.已知,△ABC的三边分别为a,b,c,其对角分别为∠A,∠B,∠C.下列条件能判定△ABC一定不是直角三角形的是( )
A.?a:b:c=
:
:
B.?b2﹣a2=c2
C.?∠A:∠B:∠C=2:3:5
D.?∠B=∠A+∠C
二、填空题(共6题)
13.如图,在扇形
中,
,点
是
的中点,点
,
分别为半径
,
上的动点.若
,则
周长的最小值为________.
14.观察下列各组勾股数,并寻找规律:
①4,3,5;??
②6,8,10;??
③8,15,17;?
④10,24,26
……
请根据你发现的规律写出第⑦组勾股数:________.
15.把一副三角板如图甲放置,其中
,
,
,斜边
,
,把三角板
绕点
顺时针旋转
得到
如图乙.这时
与
相交于点
,
与
相交于点
.线段
的长为________.
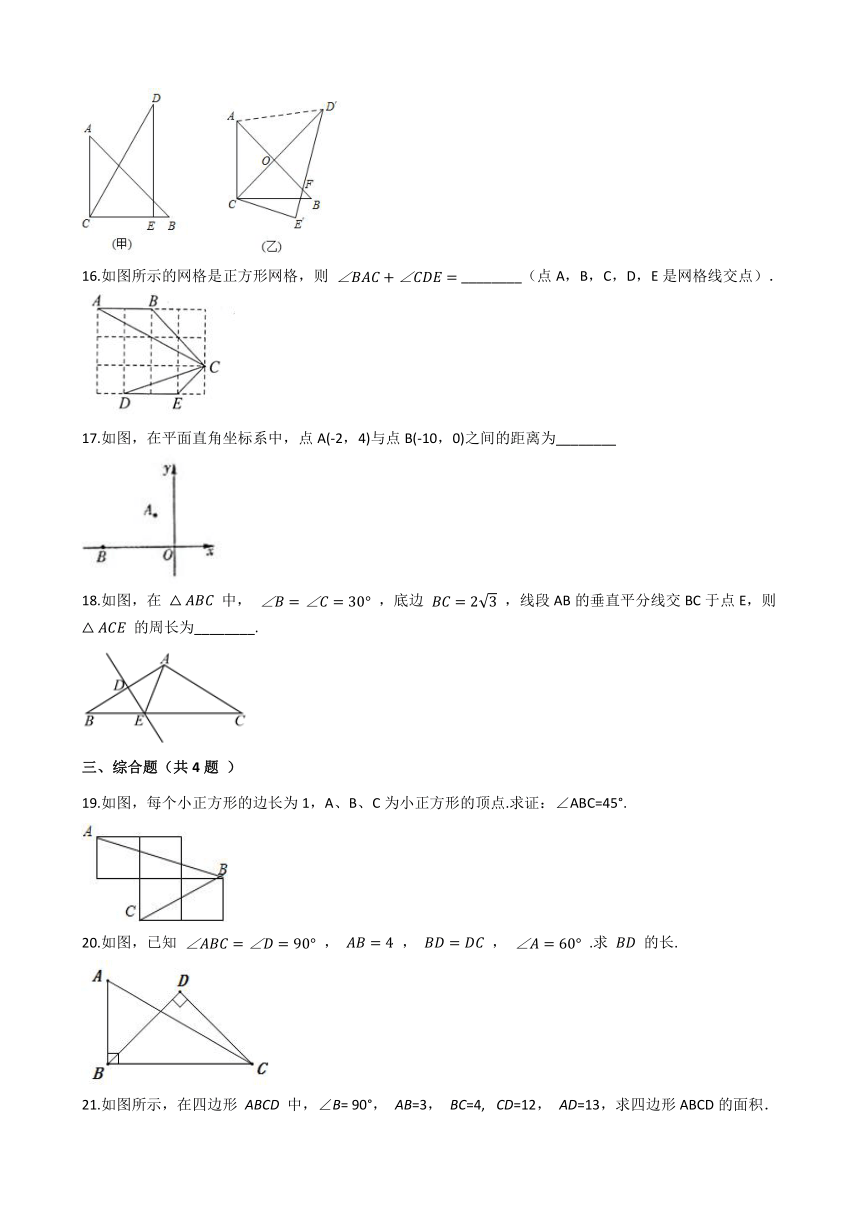
16.如图所示的网格是正方形网格,则
________(点A,B,C,D,E是网格线交点).
17.如图,在平面直角坐标系中,点A(-2,4)与点B(-10,0)之间的距离为________
18.如图,在
中,
,底边
,线段AB的垂直平分线交BC于点E,则
的周长为________.
三、综合题(共4题
)
19.如图,每个小正方形的边长为1,A、B、C为小正方形的顶点.求证:∠ABC=45°.
20.如图,已知
,
,
,
.求
的长.
21.如图所示,在四边形
ABCD
中,∠B=
90°,
AB=3,
BC=4,?
CD=12,
AD=13,求四边形ABCD的面积.
22.某中学有一块四边形的空地ABCD,如图,学校计划在空地上种植草皮,经测量∠B=90°,AB=3m,BC=4m,CD=12m,AD=13m。若每平方米草皮需费200元,问学校需要投入多少资金买草皮?
答案解析部分
一、单选题
1.【答案】
C
【解析】【解答】解:因为小正方形的边长为1,
所以,由勾股定理得,
,
,
,
∴
∴
是直角三角形,A不符合题意;
∴
,B不符合题意;
∴
,C符合题意;
设
边上的高为h
,
则有,
∴
解得,
,D不符合题意.
故答案为:C.
【分析】由勾股定理得,
,
,
,
,则
,
,
BC边上的高为h
,
则有,
,
所以选C。
2.【答案】
D
【解析】【解答】解:∵
三角形的三边长之比为1:1:
,
∴设三角形的三边长分别为x,x,x,
∵x2+x2=2x2=(x)2
,
∴
此三角形一定是等腰直角三角形.
故答案为:D.
【分析】根据题意设三角形的三边长分别为x,x,x,根据等腰三角形的定义得出此三角形是等腰三角形,再根据勾股定理的逆定理得出此三角形是直角三角形,即可得出答案.
3.【答案】
B
【解析】【解答】解:A、
,不能构成直角三角形,此项不符题意;
B、
,能构成直角三角形,此项符合题意;
C、
,不能构成直角三角形,此项不符题意;
D、
,不能构成三角形,此项不符题意;
故答案为:B.
【分析】若三角形的三边长满足a2+b2=c2
,
则该三角形为直角三角形,据此判断A、B、C;根据三角形的三边关系判断选项D.
4.【答案】
D
【解析】【解答】解:作
交
的延长线于点
,
当
时,
,
,
,
,
,
,
,
同理可得:
,
即
的长为2或4,
故答案为:
.
【分析】根据题意可画出相应的图形,再根据勾股定理,可求得CD的长,从而可求得AB的长。
5.【答案】
A
【解析】【解答】A、
,所以该三角形不是直角三角形,故该选项符合题意;
B、
,所以该三角形是直角三角形,故该选项不符合题意;
C、
,所以该三角形是直角三角形,故该选项不符合题意;
D、
,所以该三角形是直角三角形,故该选项不符合题意.
故答案为:A.
【分析】先求出各选项中较小的两数的平方和,再求出较大的数的平方,然后比较大小,可得出能构成直角三角形的选项.
6.【答案】
B
【解析】【解答】解:设这个直角三角形的两直角边为a、b,斜边为c,
根据题意得a+b=14,
ab=24,即ab=48,
∴c2=a2+b2=(a+b)2﹣2ab=142﹣2×48=100,
∴c
=10,即斜边长为10cm.
故答案为:B.
【分析】设这个直角三角形的两直角边为a、b,斜边为c,根据题意得a+b=14,
ab=24,再由勾股定理c2=a2+b2
,
代入值开平方求斜边.
7.【答案】
B
【解析】【解答】解:∵
于点
,
,
,
∴
BD=2DE,
设DE=x,则BD=2DE=2x,
∴
,
∴
,
解得:
作
于点
,
是
的角平分线,
,
,
,
∴
,
∴
在Rt△CDF中,
,
∴
故答案为:B.
【分析】作DF⊥AC于点F,设DE=x,用勾股定理可求得x的值,由角平分线的性质“角平分线上的点到角两边的距离相等”可得DE=DF,再根据等腰直角三角形的性质可得CF=DF=DE,在直角三角形CDF中,用勾股定理可求解.
8.【答案】
C
【解析】【解答】解:∵长方形ABCD的长为2,宽为1,
∴
,
∴以AC的长为半径画圆,则这个圆与数轴的交点所表示的数是±
;
故答案为:C
【分析】直接利用勾股定理得出OC的长,再利用数轴得出圆与数轴交点表示的数.
9.【答案】
B
【解析】【解答】解:A.
1.52+22=2.52
,
∴1.5,2,2.5可以作为直角三角形的三边长度,此选项不符合题意;
B.
52+122≠142
,
∴5,12,14不可以作为直角三角形的三边长度,此选项符合题意;
C.
302+402=502
,
∴30,40,50可以作为直角三角形的三边长度,此选项不符合题意;???
D.
12+(
)2=22
,
∴1,2,
可以作为直角三角形的三边长度,此选项不符合题意;
故答案为:B
【分析】先找出最大边,然后根据勾股逆定理分析判断,即直角三角形的最大边的平方等于另外两边的平方和.
10.【答案】
D
【解析】【解答】解:∵
∴
或
,即
∴该三角形为等腰三角形或直角三角形
故答案为:D.
【分析】由(a-b)(a2+b2-c2)=0,可得:a-b=0,或a2+b2-c2=0,进而可得a=b或a2+b2=c2
,
进而判断△ABC的形状为等腰三角形或直角三角形.
11.【答案】
B
【解析】【解答】解:
∵
,
设AC=5k,BC=12k,AB=13k,
∴AC2+BC2=AB2
∴
为直角三角形,∠C=90°,
∵AD是
的角平分线,
,
∴∠CAD=∠BAD,∠C=∠AED
=90°,
∵AD=AD,
∴
,
∴
,AE=AC=5k,
∴BE=13k-5k=8k,
∵
和
同高,
∴
,
∵
的面积为S,
∴
.
故答案为:B.
【分析】设AC=5k,BC=12k,AB=13k,由勾股定理的逆定理可得
为直角三角形,∠C=90°,由角平分线的性质可得DE=CD,可得Rt△ACD≌Rt△ADE,故AE=AC=5k,可得BE=13k-5k=8k,根据
和
同高,根据同高三角形的面积之比等于相似比的平方可得
,可得结果.
12.【答案】
A
【解析】【解答】解:A、∵
,
∴a2+b2≠c2
,
∴△ABC不是直角三角形,故选项A符合题意;
B、∵b2﹣a2=c2
,
∴a2+c2=b2
,
根据勾股定理逆定理可知△ABC是直角三角形,故选项B不符合题意;
C、∵∠A:∠B:∠C=2:3:5,∠A+∠B+∠C=180°,
∴∠C=
×180°=90°,即△ABC是直角三角形,故选项C不符合题意;
D、∵∠B=∠A+∠C,∠A+∠B+∠C=180°,
∴2∠B=180°,
∴∠B=90°,即△ABC是直角三角形,故选项D不符合题意.
故答案为:A.
【分析】根据勾股定理的逆定理,一个三角形的三边如果满足较小两边的平方和等于最大边长的平方,则该三角形就是直角三角形,据此即可判断A、C;由三角形中有一个内角等于90°的三角形是直角三角形,进而结合三角形的内角和定理即可判断B、D.
二、填空题
13.【答案】
【解析】【解答】解:如图,作点
关于
的对称点
,连接
,
则
,
的周长为
,
由两点之间线段最短得:当点
共线时,
周长最小,最小值为
,
,
,
,
由同圆半径相等得:
,
,
在
中,
,
即
周长的最小值为
,
故答案为:
.
【分析】如图(见解析),先根据轴对称的性质可得
,再根据两点之间线段最短可得点
共线时,
周长最小,然后利用勾股定理即可得.
14.【答案】
16,63,65
【解析】【解答】解:根据①4,3,5;②6,8,10;③8,15,17;④10,24,26
……
可得这组数中的第一个数是2(n+1),第二个是:n(n+2),第三个数是:(n+1)2+1
因此可求第⑦个数为:16,63,65.
故答案为16,63,65.
【分析】根据题意,由勾股数的定义以及规律,证明得到答案即可。
15.【答案】
5
【解析】【解答】解:由题意易知:∠CAB=45°,∠ACD=30°.
若旋转角度为15°,则∠ACO=30°+15°=45°.
∴∠AOC=180°-∠ACO-∠CAO=90°.
在等腰Rt△ABC中,AB=6,则AC=BC=AB?
=3
.
同理可求得:AO=OC=3.
在Rt△AO
中,OA=3,O
=C
-OC=4,
由勾股定理得:A
=
=5.
故答案为:5.
【分析】先求出∠ACD=30°,根据旋转角求出∠ACO=45°,然后判断出△ACO是等腰直角三角形,在等腰Rt△ABC中,求出AC=BC=3
,
从而求出AO=OC=3,继而得出O
=C
-OC=4,在Rt△AO
中,利用勾股定理即可求出结论.
16.【答案】
【解析】【解答】连接AD,如图:
∵
,
,
,
即
,
∴△ADC是等腰直角三角形,且∠ADC
,
∴∠ACD
,
∵∠BAC=∠ACF,∠CDE=∠DCF,
∴∠BAC+∠CDE=∠ACF
+∠DCF=∠ACD
,
故答案为:
.
【分析】连接AD,利用勾股定理逆定理证明△ADC是等腰直角三角形,再利用角的运算求解即可。
17.【答案】
【解析】【解答】解:∵A(-2,4),B(-10,0),
∴AB=.
【分析】根据勾股定理列式进行计算,即可得出答案.
18.【答案】
2+2
【解析】【解答】解:∵DE垂直平分AB,∠B=∠C=30°,
∴BE=AE,∠B=∠BAE=30°,
∴∠CAE=180°-∠B-∠BAE-∠C
=90°,
在Rt△CAE中,∠C=30°,
∴EC=2AE,
∴AE+EC=BE+EC=BC=2
,即3AE=2
,
∴AE=
,EC=
,
∴AC=
,
∴∴△ACE的周长=AC+AE+CE=AC+BC=2+2
,
故答案为:2+2
.
【分析】根据等腰三角形的性质,结合垂直平分线的性质,推出△CAE为含30°的直角三角形,根据BC=2列等式求出AE,然后根据勾股定理求出AC,则可△ACE的周长可求.
三、解答题
19.【答案】
证明:连接AC,
则由勾股定理可以得到:
AC=
=
,BC=
=
,AB=
=
.
∴AC2+BC2=AB2.
∴△ABC是直角三角形.
又∵AC=BC,
∴∠CAB=∠ABC.
∴∠ABC=45°.
【解析】【分析】连接AC,先依据勾股定理求得AB、AC、BC的长,然后依据勾股定理的逆定理可推出△ABC为直角三角形,然后依据AC=BC可得到△ABC为等腰直角三角形,最后根据直角三角形的性质可得结论.
20.【答案】
解:如图,
∵
,
,
∴
,
∴
∵
,
∴
>
∴
【解析】【分析】首先根据直角三角形两锐角互余得到∠ACB=30°,求出AC、BC2的值,然后在等腰Rt△BCD中应用勾股定理求解即可.
21.【答案】
解:如图所示,连接AC.
∵∠B=90°,∴ΔABC是直角三角形.
依据勾股定理得AC2=AB2+BC2=32+42=25=52
,
∴AC=5.
在ΔACD中,AD2=132=169,CD2+AC2=122+52=169,
∴AD2=AC2+CD2.
∴ΔACD是直角三角形,∠ACD=90°.
∴S四边形ABCD=SΔABC+SΔACD
=
AB?BC+
AC?CD
=
×4×3+
×5×12
=6+30=36.
∴四边形ABCD的面积为36.
【解析】【分析】考查勾股定理及逆定理的运用,连接AC,先在三△ABC中根据
∠B=
90°,?AB=3,?BC=4,?
计算出AC=5,再在△ACD中,根据勾股定理逆定理确定△ACD为直角三角形,然后分别计算出两个三角形的面积并相加。
22.【答案】
解:连接AC,∵∠B=
90°,AB
=
3m,BC
=
4m,∴AC=
5m,∴AC2+CD2=
25+144
=
169=
132
,
又∵AD2
=
132
,∴AC2
+CD2
=
AD2
,
∴∠ACD
=
90°,
∴△ACD是直角三角形,四边形ABCD的面积=6+30=
36(m2),学校需要投入资金为:200
×36
=
7200(元)
答:学校需要投入7200元买草皮.
【解析】【分析】
连接AC,根据勾股定理求出AC的长,再根据勾股定理的逆定理证出△ACD是直角三角形,从而求出四边形ABCD的面积,再乘以200元进行计算,即可得出答
一、单选题(共12题)
1.如图,在
的正方形网格图中,小正方形的边长为1,
的顶点均在格点上,则下列关于
的说法错误的是(??
)
A.?是直角三角形??????????????????B.?tam
??????????????????C.?面积为
??????????????????D.?
边上的高为
2.已知三角形的三边长之比为1:1:
,则此三角形一定是(??
)
A.?锐角三角形????????????????????B.?钝角三角形????????????????????C.?等边三角形????????????????????D.?等腰直角三角形
3.下列各组数中,能构成直角三角形的是(??
)
A.?3,4,6?????????????????????????B.?1,1,
?????????????????????????C.?6,8,11?????????????????????????D.?5,12,23
4.在
中,
,
,
,则
的长为(???
)
A.?1??????????????????????????????????????B.?2??????????????????????????????????????C.?
或4??????????????????????????????????????D.?2或4
5.在下列由线段a,b,c的长为三边的三角形中,不能构成直角三角形的是(??
)
A.?a=4,b=5,c=6
B.?a=12,b=5,c=13
C.?a=6,b=8,c=10
D.?a=7,b=24,c=25
6.一个直角三角形的两条直角边的和是14cm,面积是24cm2
,
则其斜边长为(?
)
A.?2
cm???????????????????????????????B.?10cm???????????????????????????????C.?8cm???????????????????????????????D.?4
cm
7.如图,在
中,
是
的角平分线,
于点
,
,
,
,则
长是(??
)
A.?1?????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?2
8.将一个长为2,宽为1的长方形ABCD按如图方式放在数轴上,使点A与原点O重合,若以O为圆心,以AC的长为半径画圆,则这个圆与数轴的交点所表示的数是(
?)
A.?????????????????????????????????????B.?﹣
????????????????????????????????????C.?±
????????????????????????????????????D.?±2.5
9.下列几组数中,不能作为直角三角形三边长度的是(??
)
A.?1.5,2,2.5??????????????????????B.?5,12,14??????????????????????C.?30,40,50??????????????????????D.?1,2,
10.已知a、b、c为
的三边,且满足
,则
是(??
)
A.?等腰三角形?????????????B.?直角三角形?????????????C.?等腰直角三角形?????????????D.?等腰三角形或直角三角形
11.在
中,已知
,AD是
的角平分线,
于点E.若
的面积为S,则
的面积为(??
)
A.??????????????????????????????????????B.??????????????????????????????????????C.??????????????????????????????????????D.?
12.已知,△ABC的三边分别为a,b,c,其对角分别为∠A,∠B,∠C.下列条件能判定△ABC一定不是直角三角形的是( )
A.?a:b:c=
:
:
B.?b2﹣a2=c2
C.?∠A:∠B:∠C=2:3:5
D.?∠B=∠A+∠C
二、填空题(共6题)
13.如图,在扇形
中,
,点
是
的中点,点
,
分别为半径
,
上的动点.若
,则
周长的最小值为________.
14.观察下列各组勾股数,并寻找规律:
①4,3,5;??
②6,8,10;??
③8,15,17;?
④10,24,26
……
请根据你发现的规律写出第⑦组勾股数:________.
15.把一副三角板如图甲放置,其中
,
,
,斜边
,
,把三角板
绕点
顺时针旋转
得到
如图乙.这时
与
相交于点
,
与
相交于点
.线段
的长为________.
16.如图所示的网格是正方形网格,则
________(点A,B,C,D,E是网格线交点).
17.如图,在平面直角坐标系中,点A(-2,4)与点B(-10,0)之间的距离为________
18.如图,在
中,
,底边
,线段AB的垂直平分线交BC于点E,则
的周长为________.
三、综合题(共4题
)
19.如图,每个小正方形的边长为1,A、B、C为小正方形的顶点.求证:∠ABC=45°.
20.如图,已知
,
,
,
.求
的长.
21.如图所示,在四边形
ABCD
中,∠B=
90°,
AB=3,
BC=4,?
CD=12,
AD=13,求四边形ABCD的面积.
22.某中学有一块四边形的空地ABCD,如图,学校计划在空地上种植草皮,经测量∠B=90°,AB=3m,BC=4m,CD=12m,AD=13m。若每平方米草皮需费200元,问学校需要投入多少资金买草皮?
答案解析部分
一、单选题
1.【答案】
C
【解析】【解答】解:因为小正方形的边长为1,
所以,由勾股定理得,
,
,
,
∴
∴
是直角三角形,A不符合题意;
∴
,B不符合题意;
∴
,C符合题意;
设
边上的高为h
,
则有,
∴
解得,
,D不符合题意.
故答案为:C.
【分析】由勾股定理得,
,
,
,
,则
,
,
BC边上的高为h
,
则有,
,
所以选C。
2.【答案】
D
【解析】【解答】解:∵
三角形的三边长之比为1:1:
,
∴设三角形的三边长分别为x,x,x,
∵x2+x2=2x2=(x)2
,
∴
此三角形一定是等腰直角三角形.
故答案为:D.
【分析】根据题意设三角形的三边长分别为x,x,x,根据等腰三角形的定义得出此三角形是等腰三角形,再根据勾股定理的逆定理得出此三角形是直角三角形,即可得出答案.
3.【答案】
B
【解析】【解答】解:A、
,不能构成直角三角形,此项不符题意;
B、
,能构成直角三角形,此项符合题意;
C、
,不能构成直角三角形,此项不符题意;
D、
,不能构成三角形,此项不符题意;
故答案为:B.
【分析】若三角形的三边长满足a2+b2=c2
,
则该三角形为直角三角形,据此判断A、B、C;根据三角形的三边关系判断选项D.
4.【答案】
D
【解析】【解答】解:作
交
的延长线于点
,
当
时,
,
,
,
,
,
,
,
同理可得:
,
即
的长为2或4,
故答案为:
.
【分析】根据题意可画出相应的图形,再根据勾股定理,可求得CD的长,从而可求得AB的长。
5.【答案】
A
【解析】【解答】A、
,所以该三角形不是直角三角形,故该选项符合题意;
B、
,所以该三角形是直角三角形,故该选项不符合题意;
C、
,所以该三角形是直角三角形,故该选项不符合题意;
D、
,所以该三角形是直角三角形,故该选项不符合题意.
故答案为:A.
【分析】先求出各选项中较小的两数的平方和,再求出较大的数的平方,然后比较大小,可得出能构成直角三角形的选项.
6.【答案】
B
【解析】【解答】解:设这个直角三角形的两直角边为a、b,斜边为c,
根据题意得a+b=14,
ab=24,即ab=48,
∴c2=a2+b2=(a+b)2﹣2ab=142﹣2×48=100,
∴c
=10,即斜边长为10cm.
故答案为:B.
【分析】设这个直角三角形的两直角边为a、b,斜边为c,根据题意得a+b=14,
ab=24,再由勾股定理c2=a2+b2
,
代入值开平方求斜边.
7.【答案】
B
【解析】【解答】解:∵
于点
,
,
,
∴
BD=2DE,
设DE=x,则BD=2DE=2x,
∴
,
∴
,
解得:
作
于点
,
是
的角平分线,
,
,
,
∴
,
∴
在Rt△CDF中,
,
∴
故答案为:B.
【分析】作DF⊥AC于点F,设DE=x,用勾股定理可求得x的值,由角平分线的性质“角平分线上的点到角两边的距离相等”可得DE=DF,再根据等腰直角三角形的性质可得CF=DF=DE,在直角三角形CDF中,用勾股定理可求解.
8.【答案】
C
【解析】【解答】解:∵长方形ABCD的长为2,宽为1,
∴
,
∴以AC的长为半径画圆,则这个圆与数轴的交点所表示的数是±
;
故答案为:C
【分析】直接利用勾股定理得出OC的长,再利用数轴得出圆与数轴交点表示的数.
9.【答案】
B
【解析】【解答】解:A.
1.52+22=2.52
,
∴1.5,2,2.5可以作为直角三角形的三边长度,此选项不符合题意;
B.
52+122≠142
,
∴5,12,14不可以作为直角三角形的三边长度,此选项符合题意;
C.
302+402=502
,
∴30,40,50可以作为直角三角形的三边长度,此选项不符合题意;???
D.
12+(
)2=22
,
∴1,2,
可以作为直角三角形的三边长度,此选项不符合题意;
故答案为:B
【分析】先找出最大边,然后根据勾股逆定理分析判断,即直角三角形的最大边的平方等于另外两边的平方和.
10.【答案】
D
【解析】【解答】解:∵
∴
或
,即
∴该三角形为等腰三角形或直角三角形
故答案为:D.
【分析】由(a-b)(a2+b2-c2)=0,可得:a-b=0,或a2+b2-c2=0,进而可得a=b或a2+b2=c2
,
进而判断△ABC的形状为等腰三角形或直角三角形.
11.【答案】
B
【解析】【解答】解:
∵
,
设AC=5k,BC=12k,AB=13k,
∴AC2+BC2=AB2
∴
为直角三角形,∠C=90°,
∵AD是
的角平分线,
,
∴∠CAD=∠BAD,∠C=∠AED
=90°,
∵AD=AD,
∴
,
∴
,AE=AC=5k,
∴BE=13k-5k=8k,
∵
和
同高,
∴
,
∵
的面积为S,
∴
.
故答案为:B.
【分析】设AC=5k,BC=12k,AB=13k,由勾股定理的逆定理可得
为直角三角形,∠C=90°,由角平分线的性质可得DE=CD,可得Rt△ACD≌Rt△ADE,故AE=AC=5k,可得BE=13k-5k=8k,根据
和
同高,根据同高三角形的面积之比等于相似比的平方可得
,可得结果.
12.【答案】
A
【解析】【解答】解:A、∵
,
∴a2+b2≠c2
,
∴△ABC不是直角三角形,故选项A符合题意;
B、∵b2﹣a2=c2
,
∴a2+c2=b2
,
根据勾股定理逆定理可知△ABC是直角三角形,故选项B不符合题意;
C、∵∠A:∠B:∠C=2:3:5,∠A+∠B+∠C=180°,
∴∠C=
×180°=90°,即△ABC是直角三角形,故选项C不符合题意;
D、∵∠B=∠A+∠C,∠A+∠B+∠C=180°,
∴2∠B=180°,
∴∠B=90°,即△ABC是直角三角形,故选项D不符合题意.
故答案为:A.
【分析】根据勾股定理的逆定理,一个三角形的三边如果满足较小两边的平方和等于最大边长的平方,则该三角形就是直角三角形,据此即可判断A、C;由三角形中有一个内角等于90°的三角形是直角三角形,进而结合三角形的内角和定理即可判断B、D.
二、填空题
13.【答案】
【解析】【解答】解:如图,作点
关于
的对称点
,连接
,
则
,
的周长为
,
由两点之间线段最短得:当点
共线时,
周长最小,最小值为
,
,
,
,
由同圆半径相等得:
,
,
在
中,
,
即
周长的最小值为
,
故答案为:
.
【分析】如图(见解析),先根据轴对称的性质可得
,再根据两点之间线段最短可得点
共线时,
周长最小,然后利用勾股定理即可得.
14.【答案】
16,63,65
【解析】【解答】解:根据①4,3,5;②6,8,10;③8,15,17;④10,24,26
……
可得这组数中的第一个数是2(n+1),第二个是:n(n+2),第三个数是:(n+1)2+1
因此可求第⑦个数为:16,63,65.
故答案为16,63,65.
【分析】根据题意,由勾股数的定义以及规律,证明得到答案即可。
15.【答案】
5
【解析】【解答】解:由题意易知:∠CAB=45°,∠ACD=30°.
若旋转角度为15°,则∠ACO=30°+15°=45°.
∴∠AOC=180°-∠ACO-∠CAO=90°.
在等腰Rt△ABC中,AB=6,则AC=BC=AB?
=3
.
同理可求得:AO=OC=3.
在Rt△AO
中,OA=3,O
=C
-OC=4,
由勾股定理得:A
=
=5.
故答案为:5.
【分析】先求出∠ACD=30°,根据旋转角求出∠ACO=45°,然后判断出△ACO是等腰直角三角形,在等腰Rt△ABC中,求出AC=BC=3
,
从而求出AO=OC=3,继而得出O
=C
-OC=4,在Rt△AO
中,利用勾股定理即可求出结论.
16.【答案】
【解析】【解答】连接AD,如图:
∵
,
,
,
即
,
∴△ADC是等腰直角三角形,且∠ADC
,
∴∠ACD
,
∵∠BAC=∠ACF,∠CDE=∠DCF,
∴∠BAC+∠CDE=∠ACF
+∠DCF=∠ACD
,
故答案为:
.
【分析】连接AD,利用勾股定理逆定理证明△ADC是等腰直角三角形,再利用角的运算求解即可。
17.【答案】
【解析】【解答】解:∵A(-2,4),B(-10,0),
∴AB=.
【分析】根据勾股定理列式进行计算,即可得出答案.
18.【答案】
2+2
【解析】【解答】解:∵DE垂直平分AB,∠B=∠C=30°,
∴BE=AE,∠B=∠BAE=30°,
∴∠CAE=180°-∠B-∠BAE-∠C
=90°,
在Rt△CAE中,∠C=30°,
∴EC=2AE,
∴AE+EC=BE+EC=BC=2
,即3AE=2
,
∴AE=
,EC=
,
∴AC=
,
∴∴△ACE的周长=AC+AE+CE=AC+BC=2+2
,
故答案为:2+2
.
【分析】根据等腰三角形的性质,结合垂直平分线的性质,推出△CAE为含30°的直角三角形,根据BC=2列等式求出AE,然后根据勾股定理求出AC,则可△ACE的周长可求.
三、解答题
19.【答案】
证明:连接AC,
则由勾股定理可以得到:
AC=
=
,BC=
=
,AB=
=
.
∴AC2+BC2=AB2.
∴△ABC是直角三角形.
又∵AC=BC,
∴∠CAB=∠ABC.
∴∠ABC=45°.
【解析】【分析】连接AC,先依据勾股定理求得AB、AC、BC的长,然后依据勾股定理的逆定理可推出△ABC为直角三角形,然后依据AC=BC可得到△ABC为等腰直角三角形,最后根据直角三角形的性质可得结论.
20.【答案】
解:如图,
∵
,
,
∴
,
∴
∵
,
∴
>
∴
【解析】【分析】首先根据直角三角形两锐角互余得到∠ACB=30°,求出AC、BC2的值,然后在等腰Rt△BCD中应用勾股定理求解即可.
21.【答案】
解:如图所示,连接AC.
∵∠B=90°,∴ΔABC是直角三角形.
依据勾股定理得AC2=AB2+BC2=32+42=25=52
,
∴AC=5.
在ΔACD中,AD2=132=169,CD2+AC2=122+52=169,
∴AD2=AC2+CD2.
∴ΔACD是直角三角形,∠ACD=90°.
∴S四边形ABCD=SΔABC+SΔACD
=
AB?BC+
AC?CD
=
×4×3+
×5×12
=6+30=36.
∴四边形ABCD的面积为36.
【解析】【分析】考查勾股定理及逆定理的运用,连接AC,先在三△ABC中根据
∠B=
90°,?AB=3,?BC=4,?
计算出AC=5,再在△ACD中,根据勾股定理逆定理确定△ACD为直角三角形,然后分别计算出两个三角形的面积并相加。
22.【答案】
解:连接AC,∵∠B=
90°,AB
=
3m,BC
=
4m,∴AC=
5m,∴AC2+CD2=
25+144
=
169=
132
,
又∵AD2
=
132
,∴AC2
+CD2
=
AD2
,
∴∠ACD
=
90°,
∴△ACD是直角三角形,四边形ABCD的面积=6+30=
36(m2),学校需要投入资金为:200
×36
=
7200(元)
答:学校需要投入7200元买草皮.
【解析】【分析】
连接AC,根据勾股定理求出AC的长,再根据勾股定理的逆定理证出△ACD是直角三角形,从而求出四边形ABCD的面积,再乘以200元进行计算,即可得出答
