《26.1 二次函数》同步练习2020-2021学年华东师大版数学九年级下册(Word版 含答案)
文档属性
| 名称 | 《26.1 二次函数》同步练习2020-2021学年华东师大版数学九年级下册(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 262.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-30 23:17:52 | ||
图片预览




文档简介
《26.1
二次函数》同步练习2020-2021年数学华东师大版九(下)
一.选择题(共9小题)
1.下列函数中,是二次函数的是( )
A.y=3x﹣2
B.y=
C.y=x2+1
D.y=(x﹣1)2﹣x2
2.若函数y=(1+m)x是关于x的二次函数,则m的值是( )
A.2
B.﹣1或3
C.3
D.﹣1±
3.当函数是二次函数时,a的取值为( )
A.a=1
B.a=±1
C.a≠1
D.a=﹣1
4.今年由于受新型冠状病毒的影响,一次性医用口罩的销量剧增.某药店一月份销售量是5000枚,二、三两个月销售量连续增长.若月平均增长率为x,则该药店三月份销售口罩枚数y(枚)与x的函数关系式是( )
A.y=5000(1+x)
B.y=5000(1+x)2
C.y=5000(1+x2)
D.y=5000(1+2x)
5.下列y关于x的函数中,一定是二次函数的是( )
A.y=(k﹣1)x2+3
B.y=+1
C.y=(x+1)(x﹣2)﹣x2
D.y=2x2﹣7x
6.下列函数:①y=3﹣;②y=;③y=x(3﹣5x);④y=(1+2x)(1﹣2x),是二次函数的有( )
A.1个
B.2个
C.3个
D.4个
7.如图,在△ABC中,AB=AC,BC=6,E为AC边上的点且AE=2EC,点D在BC边上且满足BD=DE,设BD=y,S△ABC=x,则y与x的函数关系式为( )
A.y=x2+
B.y=x2+
C.y=x2+2
D.y=x2+2
8.如图,在Rt△ABO中,AB⊥OB,且AB=OB=3,设直线x=t截此三角形所得的阴影部分的面积为S,则S与t之间的函数关系式为( )
A.S=t(0<t≤3)
B.S=t2(0<t≤3)
C.S=t2(0<t≤3)
D.S=t2﹣1(0<t≤3)
9.某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边用长为40米的篱笆围成,已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米,围成的苗圃面积为y,则y关于x的函数关系式为( )
A.y=x(40﹣x)
B.y=x(18﹣x)
C.y=x(40﹣2x)
D.y=2x(40﹣2x)
二.填空题(共4小题)
10.若y=(m2+m)xm2﹣2m﹣1﹣x+3是关于x的二次函数,则m=
.
11.如图,正方形EFGH的顶点在边长为2的正方形的边上.若设AE=x,正方形EFGH的面积为y,则y与x的函数关系为
.
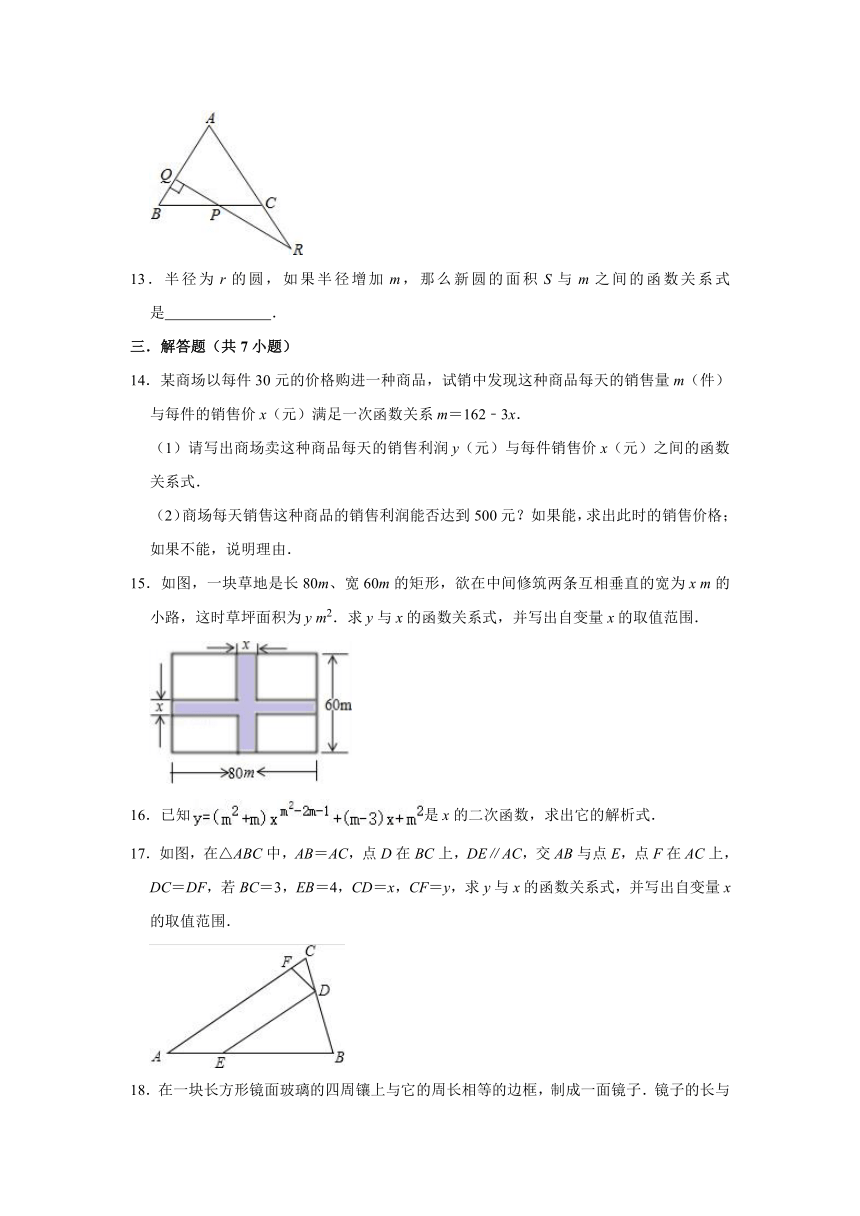
12.如图所示,P是边长为1的正三角形ABC的BC边上一点,从P向AB作垂线PQ,Q为垂足.延长QP与AC的延长线交于R,设BP=x(0≤x≤1),△BPQ与△CPR的面积之和为y,把y表示为x的函数是
.
13.半径为r的圆,如果半径增加m,那么新圆的面积S与m之间的函数关系式是
.
三.解答题(共7小题)
14.某商场以每件30元的价格购进一种商品,试销中发现这种商品每天的销售量m(件)与每件的销售价x(元)满足一次函数关系m=162﹣3x.
(1)请写出商场卖这种商品每天的销售利润y(元)与每件销售价x(元)之间的函数关系式.
(2)商场每天销售这种商品的销售利润能否达到500元?如果能,求出此时的销售价格;如果不能,说明理由.
15.如图,一块草地是长80m、宽60m的矩形,欲在中间修筑两条互相垂直的宽为x
m的小路,这时草坪面积为y
m2.求y与x的函数关系式,并写出自变量x的取值范围.
16.已知是x的二次函数,求出它的解析式.
17.如图,在△ABC中,AB=AC,点D在BC上,DE∥AC,交AB与点E,点F在AC上,DC=DF,若BC=3,EB=4,CD=x,CF=y,求y与x的函数关系式,并写出自变量x的取值范围.
18.在一块长方形镜面玻璃的四周镶上与它的周长相等的边框,制成一面镜子.镜子的长与宽的比是2:1.已知镜面玻璃的价格是每平方米120元,边框的价格是每米30元,另外制作这面镜子还需加工费45元.设制作这面镜子的总费用是y元,镜子的宽度是x米.
(1)求y与x之间的关系式.
(2)如果制作这面镜子共花了195元,求这面镜子的长和宽.
19.某商场购进一种单价为40元的商品,如果以单价60元售出,那么每天可卖出300个,根据销售经验,每降价1元,每天可多卖出20个,假设每个降价x(元),每天销售y(个),每天获得利润W(元).
(1)写出y与x的函数关系式
;
(2)求出W与x的函数关系式(不必写出x的取值范围)
20.已知等边△ABC和Rt△DEF按如图所示的位置放置,点B、D重合,且点E、B(D)、C在同一条直线上.其中∠E=90°,∠EDF=30°,AB=DE=,现将△DEF沿直线BC以每秒个单位向右平移,直至E点与C点重合时停止运动,设运动时间为t秒.
(1)试求出在平移过程中,点F落在△ABC的边上时的t值;
(2)试求出在平移过程中△ABC和Rt△DEF重叠部分的面积S与t的函数关系式.
参考答案
一.选择题(共9小题)
1.解:A、是一次函数,不是二次函数,故此选项不合题意;
B、等式右边不是整式,故不是二次函数,故此选项不符合题意;
C、是二次函数,故此选项符合题意;
D、y=(x﹣1)2﹣x2=﹣2x+1,是一次函数,不是二次函数,故此选项不合题意;
故选:C.
2.解:由题意得:m2﹣2m﹣1=2,且1+m≠0,
解得:m=3,
故选:C.
3.解:∵y=(a﹣1)x+2x+3是二次函数,
∴a﹣1≠0,a2+1=2,
解得,a=﹣1,
故选:D.
4.解:该药店三月份销售口罩枚数y(枚)与x的函数关系式是:y=5000(1+x)2.
故选:B.
5.解:A、当k=1时,不是二次函数,故此选项不合题意;
B、含有分式,不是二次函数,故此选项不合题意;
C、化简后y=﹣x﹣2,不是二次函数,故此选项不合题意;
D、是二次函数,故此选项符合题意;
故选:D.
6.解:①y=3﹣;③y=x(3﹣5x);④y=(1+2x)(1﹣2x),是二次函数,共3个,
故选:C.
7.解:过A作AH⊥BC,过E作EP⊥BC,则AH∥EP,
∴HC=3,PC=1,BP=5,PE=AH,
∵BD=DE=y,
∴在Rt△EDP中,y2=(5﹣y)2+PE2,
∵x=6AH÷2=3AH,
∴y2=(5﹣y)2+,
∴y=x2+,
故选:A.
8.解:如图所示,
∵Rt△AOB中,AB⊥OB,且AB=OB=3,
∴∠AOB=∠A=45°,
∵CD⊥OB,
∴CD∥AB,
∴∠OCD=∠A,
∴∠AOD=∠OCD=45°,
∴OD=CD=t,
∴S△OCD=×OD×CD
=t2(0<t≤3),即S=t2(0<t≤3).
故选:B.
9.解:设这个苗圃园垂直于墙的一边长为x米,则苗圃园与墙平行的一边长为(40﹣2x)米.
依题意可得:y=x(40﹣2x).
故选:C.
二.填空题(共4小题)
10.解:由题意,得
m2﹣2m﹣1=2,且m2+m≠0,
解得m=3,
故答案为:3.
11.解:如图所示:
∵四边形ABCD是边长为2的正方形,
∴∠A=∠B=90°,AB=2.
∴∠1+∠2=90°,
∵四边形EFGH为正方形,
∴∠HEF=90°,EH=EF.
∴∠1+∠3=90°,
∴∠2=∠3,
在△AHE与△BEF中,
∵,
∴△AHE≌△BEF(AAS),
∴AE=BF=x,AH=BE=2﹣x,
在Rt△AHE中,由勾股定理得:
EH2=AE2+AH2=x2+(2﹣x)2=2x2﹣4x+4;
即y=2x2﹣4x+4(0<x<2),
故答案为:y=2x2﹣4x+4.
12.解:∵BP=x,∠B=60°,∠PQB=90°,
∴BQ=x,QP=x,PC=1﹣x.
∴△BPQ的面积=×BQ×QP=x2,那么AQ=1﹣x,可得到QR=﹣x,
则PR=﹣x.
过点R做RD⊥PC,则RD=,
∴△CPR的面积=×PC×RD=.
∵△BPQ与△CPR的面积之和为y,
∴y=(3x2﹣4x+2)=x2﹣x+,
∴y=x2﹣x+.
13.解:新圆的半径是(r+m),则S与m之间的函数关系式是:S=π(r+m)2.
三.解答题(共7小题)
14.解:(1)由题意得,每件商品的销售利润为(x﹣30)元,那么m件的销售利润为y=m(x﹣30),
又∵m=162﹣3x,
∴y=(x﹣30)(162﹣3x),
即y=﹣3x2+252x﹣4860,
∵x﹣30≥0,
∴x≥30.
又∵m≥0,
∴162﹣3x≥0,即x≤54.
∴30≤x≤54.
∴所求关系式为y=﹣3x2+252x﹣4860(30≤x≤54).
(2)由(1)得y=﹣3x2+252x﹣4860=﹣3(x﹣42)2+432,
所以可得售价定为42元时获得的利润最大,最大销售利润是432元.
∵500>432,
∴商场每天销售这种商品的销售利润不能达到500元.
15.解:由题意得:
y=(80﹣x)(60﹣x),
=x2﹣140x+4800(0<x<60).
所以函数关系式为:
y=x2﹣140x+4800(0<x<60).
16.解:由二次函数的定义,可知m2+m≠0,即m≠0,m≠﹣1
又因为m2﹣2m﹣1=2,m2﹣2m﹣3=0
解得m=3或m=﹣1(不合题意,舍去)
所以m=3
故y=12x2+9.
17.解:∵AB=AC,DC=DF
∴∠B=∠C=∠DFC
又∵DE∥AC
∴∠BDE=∠C
∴△BDE∽△FCD
∴
∴
∴
自变量x的取值范围0<x<3.
18.解:(1)y=(2x+2x+x+x)×30+45+2x2×120
=240x2+180x+45;
(2)由题意可列方程为
240x2+180x+45=195,
整理得8x2+6x﹣5=0,即(2x﹣1)(4x+5)=0,
解得x1=0.5,x2=﹣1.25(舍去)
∴x=0.5,
∴2x=1,
答:镜子的长和宽分别是1m和0.5m.
19.解:(1)设每个降价x(元),每天销售y(个),
y与x的函数关系式为:y=300+20x;
故答案为:y=300+20x;
(2)由题意可得,W与x的函数关系式为:
W=(300+20x)(60﹣40﹣x)
=﹣20x2+100x+6000.
20.解:
(1)当F在边AB上时,如图1,作AM⊥BC,
则AM=AB==9
∵AM⊥BC,∠FEB=90°
∴EF∥AM
∴△BEF∽△BMA
∴,即,解得BE=2,则移动的距离为:6+2=8,则t==8
当F在AC上时,如图2
同理可得,EC=2,则移动的距离为2×==10,则t==10
故t的值为:8秒或10秒
(2)当0<t≤6时,重合部分是△BND,如图,
设AB与DF交于点N,
则BD=t,NB=BD=t,ND=BD==t
S=NB?ND==
当6<t≤8时,重合部分为五边形MNQCE,如图4
S五边形MNQCE=S△FED﹣S△MNF﹣S△CQD
=18﹣?[6﹣(﹣6)]?[6﹣(t﹣6)]﹣(﹣6)?(﹣6)
=t2+33t﹣105
当8<t≤10时,重叠部分是四边形EFMC,如图5
S=S四边形EFMC=S△EDF﹣S△CDM
=18﹣(144﹣36t﹣t2)﹣(3t2﹣36t+108)
=﹣t2+27﹣81
当10<t≤12时,重合部分为△MCE,如图6
S=S△EMC=[6﹣(t﹣6)]??[6﹣(﹣6)]
=﹣36+216
综上所述,S=.
二次函数》同步练习2020-2021年数学华东师大版九(下)
一.选择题(共9小题)
1.下列函数中,是二次函数的是( )
A.y=3x﹣2
B.y=
C.y=x2+1
D.y=(x﹣1)2﹣x2
2.若函数y=(1+m)x是关于x的二次函数,则m的值是( )
A.2
B.﹣1或3
C.3
D.﹣1±
3.当函数是二次函数时,a的取值为( )
A.a=1
B.a=±1
C.a≠1
D.a=﹣1
4.今年由于受新型冠状病毒的影响,一次性医用口罩的销量剧增.某药店一月份销售量是5000枚,二、三两个月销售量连续增长.若月平均增长率为x,则该药店三月份销售口罩枚数y(枚)与x的函数关系式是( )
A.y=5000(1+x)
B.y=5000(1+x)2
C.y=5000(1+x2)
D.y=5000(1+2x)
5.下列y关于x的函数中,一定是二次函数的是( )
A.y=(k﹣1)x2+3
B.y=+1
C.y=(x+1)(x﹣2)﹣x2
D.y=2x2﹣7x
6.下列函数:①y=3﹣;②y=;③y=x(3﹣5x);④y=(1+2x)(1﹣2x),是二次函数的有( )
A.1个
B.2个
C.3个
D.4个
7.如图,在△ABC中,AB=AC,BC=6,E为AC边上的点且AE=2EC,点D在BC边上且满足BD=DE,设BD=y,S△ABC=x,则y与x的函数关系式为( )
A.y=x2+
B.y=x2+
C.y=x2+2
D.y=x2+2
8.如图,在Rt△ABO中,AB⊥OB,且AB=OB=3,设直线x=t截此三角形所得的阴影部分的面积为S,则S与t之间的函数关系式为( )
A.S=t(0<t≤3)
B.S=t2(0<t≤3)
C.S=t2(0<t≤3)
D.S=t2﹣1(0<t≤3)
9.某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边用长为40米的篱笆围成,已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米,围成的苗圃面积为y,则y关于x的函数关系式为( )
A.y=x(40﹣x)
B.y=x(18﹣x)
C.y=x(40﹣2x)
D.y=2x(40﹣2x)
二.填空题(共4小题)
10.若y=(m2+m)xm2﹣2m﹣1﹣x+3是关于x的二次函数,则m=
.
11.如图,正方形EFGH的顶点在边长为2的正方形的边上.若设AE=x,正方形EFGH的面积为y,则y与x的函数关系为
.
12.如图所示,P是边长为1的正三角形ABC的BC边上一点,从P向AB作垂线PQ,Q为垂足.延长QP与AC的延长线交于R,设BP=x(0≤x≤1),△BPQ与△CPR的面积之和为y,把y表示为x的函数是
.
13.半径为r的圆,如果半径增加m,那么新圆的面积S与m之间的函数关系式是
.
三.解答题(共7小题)
14.某商场以每件30元的价格购进一种商品,试销中发现这种商品每天的销售量m(件)与每件的销售价x(元)满足一次函数关系m=162﹣3x.
(1)请写出商场卖这种商品每天的销售利润y(元)与每件销售价x(元)之间的函数关系式.
(2)商场每天销售这种商品的销售利润能否达到500元?如果能,求出此时的销售价格;如果不能,说明理由.
15.如图,一块草地是长80m、宽60m的矩形,欲在中间修筑两条互相垂直的宽为x
m的小路,这时草坪面积为y
m2.求y与x的函数关系式,并写出自变量x的取值范围.
16.已知是x的二次函数,求出它的解析式.
17.如图,在△ABC中,AB=AC,点D在BC上,DE∥AC,交AB与点E,点F在AC上,DC=DF,若BC=3,EB=4,CD=x,CF=y,求y与x的函数关系式,并写出自变量x的取值范围.
18.在一块长方形镜面玻璃的四周镶上与它的周长相等的边框,制成一面镜子.镜子的长与宽的比是2:1.已知镜面玻璃的价格是每平方米120元,边框的价格是每米30元,另外制作这面镜子还需加工费45元.设制作这面镜子的总费用是y元,镜子的宽度是x米.
(1)求y与x之间的关系式.
(2)如果制作这面镜子共花了195元,求这面镜子的长和宽.
19.某商场购进一种单价为40元的商品,如果以单价60元售出,那么每天可卖出300个,根据销售经验,每降价1元,每天可多卖出20个,假设每个降价x(元),每天销售y(个),每天获得利润W(元).
(1)写出y与x的函数关系式
;
(2)求出W与x的函数关系式(不必写出x的取值范围)
20.已知等边△ABC和Rt△DEF按如图所示的位置放置,点B、D重合,且点E、B(D)、C在同一条直线上.其中∠E=90°,∠EDF=30°,AB=DE=,现将△DEF沿直线BC以每秒个单位向右平移,直至E点与C点重合时停止运动,设运动时间为t秒.
(1)试求出在平移过程中,点F落在△ABC的边上时的t值;
(2)试求出在平移过程中△ABC和Rt△DEF重叠部分的面积S与t的函数关系式.
参考答案
一.选择题(共9小题)
1.解:A、是一次函数,不是二次函数,故此选项不合题意;
B、等式右边不是整式,故不是二次函数,故此选项不符合题意;
C、是二次函数,故此选项符合题意;
D、y=(x﹣1)2﹣x2=﹣2x+1,是一次函数,不是二次函数,故此选项不合题意;
故选:C.
2.解:由题意得:m2﹣2m﹣1=2,且1+m≠0,
解得:m=3,
故选:C.
3.解:∵y=(a﹣1)x+2x+3是二次函数,
∴a﹣1≠0,a2+1=2,
解得,a=﹣1,
故选:D.
4.解:该药店三月份销售口罩枚数y(枚)与x的函数关系式是:y=5000(1+x)2.
故选:B.
5.解:A、当k=1时,不是二次函数,故此选项不合题意;
B、含有分式,不是二次函数,故此选项不合题意;
C、化简后y=﹣x﹣2,不是二次函数,故此选项不合题意;
D、是二次函数,故此选项符合题意;
故选:D.
6.解:①y=3﹣;③y=x(3﹣5x);④y=(1+2x)(1﹣2x),是二次函数,共3个,
故选:C.
7.解:过A作AH⊥BC,过E作EP⊥BC,则AH∥EP,
∴HC=3,PC=1,BP=5,PE=AH,
∵BD=DE=y,
∴在Rt△EDP中,y2=(5﹣y)2+PE2,
∵x=6AH÷2=3AH,
∴y2=(5﹣y)2+,
∴y=x2+,
故选:A.
8.解:如图所示,
∵Rt△AOB中,AB⊥OB,且AB=OB=3,
∴∠AOB=∠A=45°,
∵CD⊥OB,
∴CD∥AB,
∴∠OCD=∠A,
∴∠AOD=∠OCD=45°,
∴OD=CD=t,
∴S△OCD=×OD×CD
=t2(0<t≤3),即S=t2(0<t≤3).
故选:B.
9.解:设这个苗圃园垂直于墙的一边长为x米,则苗圃园与墙平行的一边长为(40﹣2x)米.
依题意可得:y=x(40﹣2x).
故选:C.
二.填空题(共4小题)
10.解:由题意,得
m2﹣2m﹣1=2,且m2+m≠0,
解得m=3,
故答案为:3.
11.解:如图所示:
∵四边形ABCD是边长为2的正方形,
∴∠A=∠B=90°,AB=2.
∴∠1+∠2=90°,
∵四边形EFGH为正方形,
∴∠HEF=90°,EH=EF.
∴∠1+∠3=90°,
∴∠2=∠3,
在△AHE与△BEF中,
∵,
∴△AHE≌△BEF(AAS),
∴AE=BF=x,AH=BE=2﹣x,
在Rt△AHE中,由勾股定理得:
EH2=AE2+AH2=x2+(2﹣x)2=2x2﹣4x+4;
即y=2x2﹣4x+4(0<x<2),
故答案为:y=2x2﹣4x+4.
12.解:∵BP=x,∠B=60°,∠PQB=90°,
∴BQ=x,QP=x,PC=1﹣x.
∴△BPQ的面积=×BQ×QP=x2,那么AQ=1﹣x,可得到QR=﹣x,
则PR=﹣x.
过点R做RD⊥PC,则RD=,
∴△CPR的面积=×PC×RD=.
∵△BPQ与△CPR的面积之和为y,
∴y=(3x2﹣4x+2)=x2﹣x+,
∴y=x2﹣x+.
13.解:新圆的半径是(r+m),则S与m之间的函数关系式是:S=π(r+m)2.
三.解答题(共7小题)
14.解:(1)由题意得,每件商品的销售利润为(x﹣30)元,那么m件的销售利润为y=m(x﹣30),
又∵m=162﹣3x,
∴y=(x﹣30)(162﹣3x),
即y=﹣3x2+252x﹣4860,
∵x﹣30≥0,
∴x≥30.
又∵m≥0,
∴162﹣3x≥0,即x≤54.
∴30≤x≤54.
∴所求关系式为y=﹣3x2+252x﹣4860(30≤x≤54).
(2)由(1)得y=﹣3x2+252x﹣4860=﹣3(x﹣42)2+432,
所以可得售价定为42元时获得的利润最大,最大销售利润是432元.
∵500>432,
∴商场每天销售这种商品的销售利润不能达到500元.
15.解:由题意得:
y=(80﹣x)(60﹣x),
=x2﹣140x+4800(0<x<60).
所以函数关系式为:
y=x2﹣140x+4800(0<x<60).
16.解:由二次函数的定义,可知m2+m≠0,即m≠0,m≠﹣1
又因为m2﹣2m﹣1=2,m2﹣2m﹣3=0
解得m=3或m=﹣1(不合题意,舍去)
所以m=3
故y=12x2+9.
17.解:∵AB=AC,DC=DF
∴∠B=∠C=∠DFC
又∵DE∥AC
∴∠BDE=∠C
∴△BDE∽△FCD
∴
∴
∴
自变量x的取值范围0<x<3.
18.解:(1)y=(2x+2x+x+x)×30+45+2x2×120
=240x2+180x+45;
(2)由题意可列方程为
240x2+180x+45=195,
整理得8x2+6x﹣5=0,即(2x﹣1)(4x+5)=0,
解得x1=0.5,x2=﹣1.25(舍去)
∴x=0.5,
∴2x=1,
答:镜子的长和宽分别是1m和0.5m.
19.解:(1)设每个降价x(元),每天销售y(个),
y与x的函数关系式为:y=300+20x;
故答案为:y=300+20x;
(2)由题意可得,W与x的函数关系式为:
W=(300+20x)(60﹣40﹣x)
=﹣20x2+100x+6000.
20.解:
(1)当F在边AB上时,如图1,作AM⊥BC,
则AM=AB==9
∵AM⊥BC,∠FEB=90°
∴EF∥AM
∴△BEF∽△BMA
∴,即,解得BE=2,则移动的距离为:6+2=8,则t==8
当F在AC上时,如图2
同理可得,EC=2,则移动的距离为2×==10,则t==10
故t的值为:8秒或10秒
(2)当0<t≤6时,重合部分是△BND,如图,
设AB与DF交于点N,
则BD=t,NB=BD=t,ND=BD==t
S=NB?ND==
当6<t≤8时,重合部分为五边形MNQCE,如图4
S五边形MNQCE=S△FED﹣S△MNF﹣S△CQD
=18﹣?[6﹣(﹣6)]?[6﹣(t﹣6)]﹣(﹣6)?(﹣6)
=t2+33t﹣105
当8<t≤10时,重叠部分是四边形EFMC,如图5
S=S四边形EFMC=S△EDF﹣S△CDM
=18﹣(144﹣36t﹣t2)﹣(3t2﹣36t+108)
=﹣t2+27﹣81
当10<t≤12时,重合部分为△MCE,如图6
S=S△EMC=[6﹣(t﹣6)]??[6﹣(﹣6)]
=﹣36+216
综上所述,S=.
