4.3立体图形的表面展开图 同步课时作业 2021-2022学年华东师大版数学七年级上册(Word版 含答案)
文档属性
| 名称 | 4.3立体图形的表面展开图 同步课时作业 2021-2022学年华东师大版数学七年级上册(Word版 含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 224.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-30 00:00:00 | ||
图片预览

文档简介
4.3 立体图形的表面展开图
知识点
1 立体图形的表面展开图
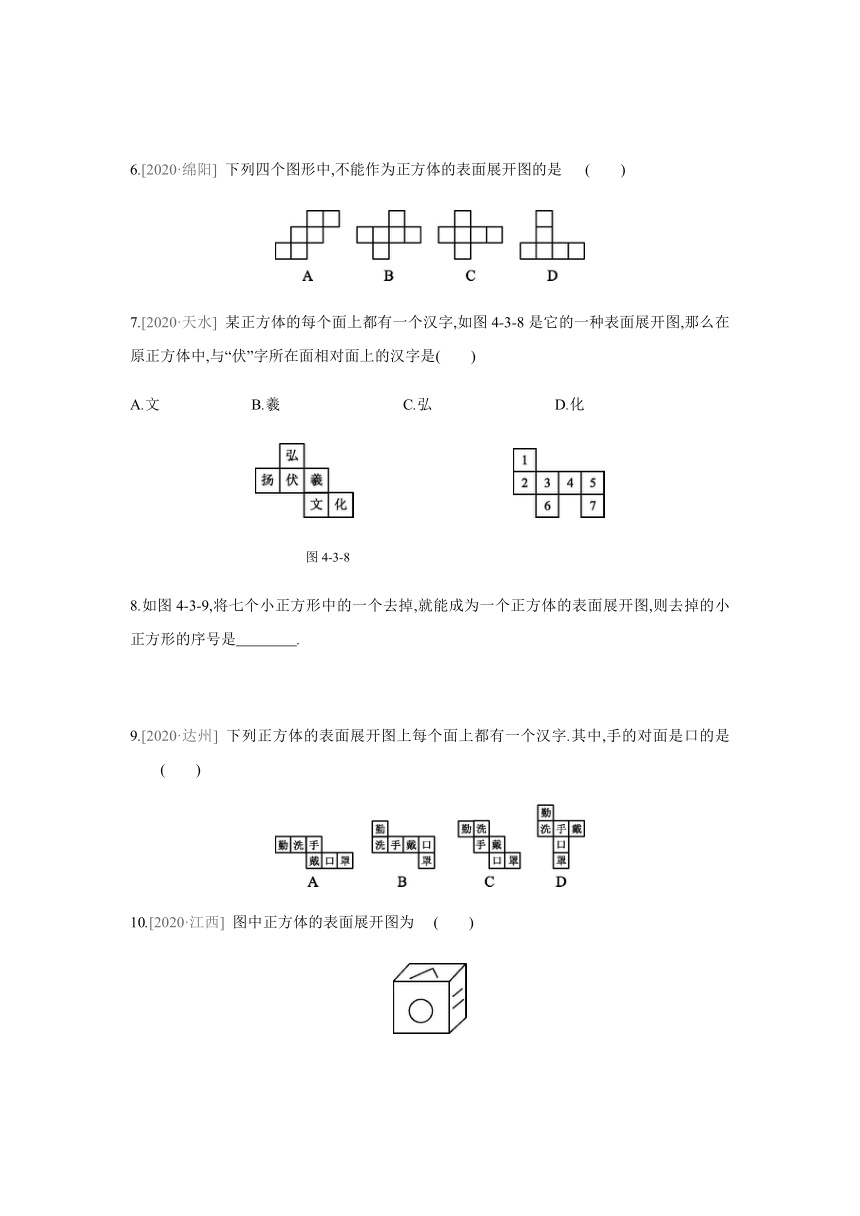
1.[2020·长春]
下列图形是四棱柱的侧面展开图的是
( )
2.[2020·衡阳]
下列不是三棱柱的表面展开图的是
( )
3.[2019·连云港]
一个几何体的侧面展开图如图4-3-3所示,则该几何体的底面是
( )
图4-3-3
4.图4-3-5是一些多面体的表面展开图,请写出它们各自的名称:
(1) ;(2) ;(3) .?
知识点
2 正方体的表面展开图
5.[2019·深圳]
下列哪个图形是正方体的表面展开图
( )
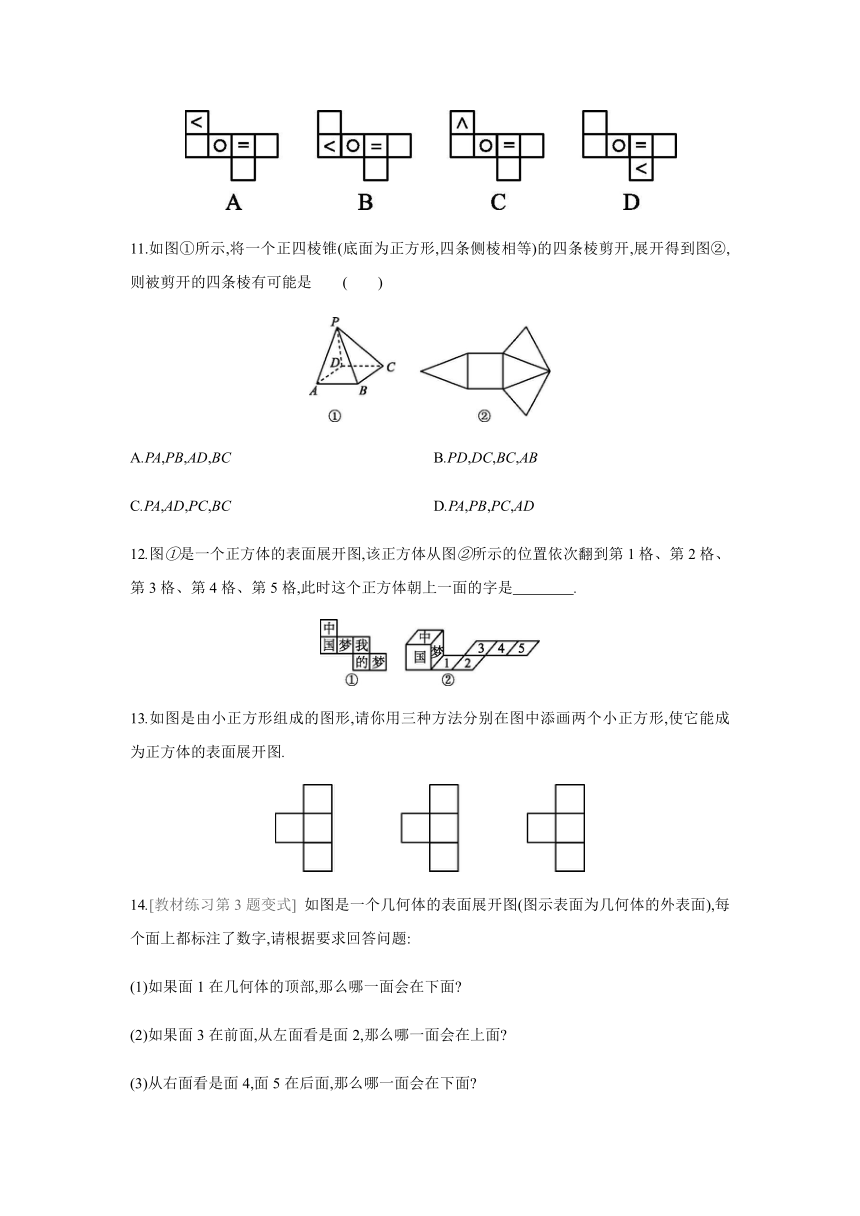
6.[2020·绵阳]
下列四个图形中,不能作为正方体的表面展开图的是
( )
7.[2020·天水]
某正方体的每个面上都有一个汉字,如图4-3-8是它的一种表面展开图,那么在原正方体中,与“伏”字所在面相对面上的汉字是( )
A.文
B.羲
C.弘
D.化
图4-3-8
8.如图4-3-9,将七个小正方形中的一个去掉,就能成为一个正方体的表面展开图,则去掉的小正方形的序号是 .?
9.[2020·达州]
下列正方体的表面展开图上每个面上都有一个汉字.其中,手的对面是口的是
( )
10.[2020·江西]
图中正方体的表面展开图为
( )
11.如图①所示,将一个正四棱锥(底面为正方形,四条侧棱相等)的四条棱剪开,展开得到图②,则被剪开的四条棱有可能是
( )
A.PA,PB,AD,BC
B.PD,DC,BC,AB
C.PA,AD,PC,BC
D.PA,PB,PC,AD
12.图①是一个正方体的表面展开图,该正方体从图②所示的位置依次翻到第1格、第2格、第3格、第4格、第5格,此时这个正方体朝上一面的字是 .?
13.如图是由小正方形组成的图形,请你用三种方法分别在图中添画两个小正方形,使它能成为正方体的表面展开图.
14.[教材练习第3题变式]
如图是一个几何体的表面展开图(图示表面为几何体的外表面),每个面上都标注了数字,请根据要求回答问题:
(1)如果面1在几何体的顶部,那么哪一面会在下面?
(2)如果面3在前面,从左面看是面2,那么哪一面会在上面?
(3)从右面看是面4,面5在后面,那么哪一面会在下面?
15.如图①所示,从大正方体中截去一个小正方体之后,可以得到图②的几何体.
(1)设原大正方体的表面积为a,图②中几何体的表面积为b,那么a与b的大小关系是
( )
A.a>b
B.aC.a=b
D.无法判断
(2)小明说:“设图①中大正方体的棱长之和为m,图②中几何体的各棱长之和为n,那么n比m正好多出大正方体的3条棱的长度.”你认为小明的说法正确吗?为什么?
(3)如果截去的小正方体的棱长为大正方体的棱长的一半,那么图③是图②几何体的表面展开图吗?如有错误,请予以改正.
答案
1.A [解析]
由四棱柱的特点可知:四棱柱的侧面展开图是长方形而且有4条棱.
故选A.
2.B [解析]
B围成三棱柱时,两个三角形重合为同一底面,而另一底面没有,故B不能围成三棱柱.故选B.
3.B
4.(1)五棱锥 (2)三棱柱 (3)四棱锥
5.B
6.D [解析]
正方体展开图的11种情况可分为“1-4-1型”6种,“2-3-1型”3种,“2-2-2型”1种,“3-3型”1种,因此选项D符合题意.
故选D.
7.D [解析]
根据正方体表面展开图可知,“相间、Z端是对面”,因此“伏”与“化”相对,“弘”与“文”相对,“扬”与“羲”相对.
故选D.
8.6或7
9.B [解析]
A.手的对面是勤,不符合题意;
B.手的对面是口,符合题意;
C.手的对面是罩,不符合题意;
D.手的对面是罩,不符合题意.
故选B.
10.A [解析]
根据“相间、Z端是对面”可得选项B不符合题意;
再根据上面“∧”符号开口,可以判断选项A符合题意,选项C,D不符合题意.
故选A.
11.A
12.我 [解析]
由图①可得,“中”和“的”相对,“国”和“我”相对,“梦”和“梦”相对.
由图②可得,该正方体从图②所示的位置依次翻到第1格、第2格、第3格、第4格、第5格时,“国”在下面,则这时小正方体朝上一面的字是“我”.
13.解:答案不唯一,如图所示:
14.解:(1)面3会在下面.
(2)面4会在上面.
(3)面3会在下面.
15.解:(1)根据“切去三个小面”但又“新增三个小面”,得与原来的表面积相等,即a=b.
故选C.
(2)小明的说法不正确.理由:如图①,加粗的棱是多出来的,共6条.
如果截去的小正方体的棱长是大正方体的棱长的一半,那么n比m正好多出大正方体的3条棱的长度;
如果截去的小正方体的棱长不是大正方体的棱长的一半,那么n就不比m多出大正方体的3条棱的长度,
故小明的说法是不正确的.
(3)不是,改正后的图形如图②所示.
知识点
1 立体图形的表面展开图
1.[2020·长春]
下列图形是四棱柱的侧面展开图的是
( )
2.[2020·衡阳]
下列不是三棱柱的表面展开图的是
( )
3.[2019·连云港]
一个几何体的侧面展开图如图4-3-3所示,则该几何体的底面是
( )
图4-3-3
4.图4-3-5是一些多面体的表面展开图,请写出它们各自的名称:
(1) ;(2) ;(3) .?
知识点
2 正方体的表面展开图
5.[2019·深圳]
下列哪个图形是正方体的表面展开图
( )
6.[2020·绵阳]
下列四个图形中,不能作为正方体的表面展开图的是
( )
7.[2020·天水]
某正方体的每个面上都有一个汉字,如图4-3-8是它的一种表面展开图,那么在原正方体中,与“伏”字所在面相对面上的汉字是( )
A.文
B.羲
C.弘
D.化
图4-3-8
8.如图4-3-9,将七个小正方形中的一个去掉,就能成为一个正方体的表面展开图,则去掉的小正方形的序号是 .?
9.[2020·达州]
下列正方体的表面展开图上每个面上都有一个汉字.其中,手的对面是口的是
( )
10.[2020·江西]
图中正方体的表面展开图为
( )
11.如图①所示,将一个正四棱锥(底面为正方形,四条侧棱相等)的四条棱剪开,展开得到图②,则被剪开的四条棱有可能是
( )
A.PA,PB,AD,BC
B.PD,DC,BC,AB
C.PA,AD,PC,BC
D.PA,PB,PC,AD
12.图①是一个正方体的表面展开图,该正方体从图②所示的位置依次翻到第1格、第2格、第3格、第4格、第5格,此时这个正方体朝上一面的字是 .?
13.如图是由小正方形组成的图形,请你用三种方法分别在图中添画两个小正方形,使它能成为正方体的表面展开图.
14.[教材练习第3题变式]
如图是一个几何体的表面展开图(图示表面为几何体的外表面),每个面上都标注了数字,请根据要求回答问题:
(1)如果面1在几何体的顶部,那么哪一面会在下面?
(2)如果面3在前面,从左面看是面2,那么哪一面会在上面?
(3)从右面看是面4,面5在后面,那么哪一面会在下面?
15.如图①所示,从大正方体中截去一个小正方体之后,可以得到图②的几何体.
(1)设原大正方体的表面积为a,图②中几何体的表面积为b,那么a与b的大小关系是
( )
A.a>b
B.a
D.无法判断
(2)小明说:“设图①中大正方体的棱长之和为m,图②中几何体的各棱长之和为n,那么n比m正好多出大正方体的3条棱的长度.”你认为小明的说法正确吗?为什么?
(3)如果截去的小正方体的棱长为大正方体的棱长的一半,那么图③是图②几何体的表面展开图吗?如有错误,请予以改正.
答案
1.A [解析]
由四棱柱的特点可知:四棱柱的侧面展开图是长方形而且有4条棱.
故选A.
2.B [解析]
B围成三棱柱时,两个三角形重合为同一底面,而另一底面没有,故B不能围成三棱柱.故选B.
3.B
4.(1)五棱锥 (2)三棱柱 (3)四棱锥
5.B
6.D [解析]
正方体展开图的11种情况可分为“1-4-1型”6种,“2-3-1型”3种,“2-2-2型”1种,“3-3型”1种,因此选项D符合题意.
故选D.
7.D [解析]
根据正方体表面展开图可知,“相间、Z端是对面”,因此“伏”与“化”相对,“弘”与“文”相对,“扬”与“羲”相对.
故选D.
8.6或7
9.B [解析]
A.手的对面是勤,不符合题意;
B.手的对面是口,符合题意;
C.手的对面是罩,不符合题意;
D.手的对面是罩,不符合题意.
故选B.
10.A [解析]
根据“相间、Z端是对面”可得选项B不符合题意;
再根据上面“∧”符号开口,可以判断选项A符合题意,选项C,D不符合题意.
故选A.
11.A
12.我 [解析]
由图①可得,“中”和“的”相对,“国”和“我”相对,“梦”和“梦”相对.
由图②可得,该正方体从图②所示的位置依次翻到第1格、第2格、第3格、第4格、第5格时,“国”在下面,则这时小正方体朝上一面的字是“我”.
13.解:答案不唯一,如图所示:
14.解:(1)面3会在下面.
(2)面4会在上面.
(3)面3会在下面.
15.解:(1)根据“切去三个小面”但又“新增三个小面”,得与原来的表面积相等,即a=b.
故选C.
(2)小明的说法不正确.理由:如图①,加粗的棱是多出来的,共6条.
如果截去的小正方体的棱长是大正方体的棱长的一半,那么n比m正好多出大正方体的3条棱的长度;
如果截去的小正方体的棱长不是大正方体的棱长的一半,那么n就不比m多出大正方体的3条棱的长度,
故小明的说法是不正确的.
(3)不是,改正后的图形如图②所示.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
