13.5.3角平分线练习题 2021-2022学年八年级数学华东师大版上册(Word版 含答案)
文档属性
| 名称 | 13.5.3角平分线练习题 2021-2022学年八年级数学华东师大版上册(Word版 含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 207.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-30 00:00:00 | ||
图片预览



文档简介
13.5.3 角平分线
【基础练习】
知识点
1 角平分线的性质定理
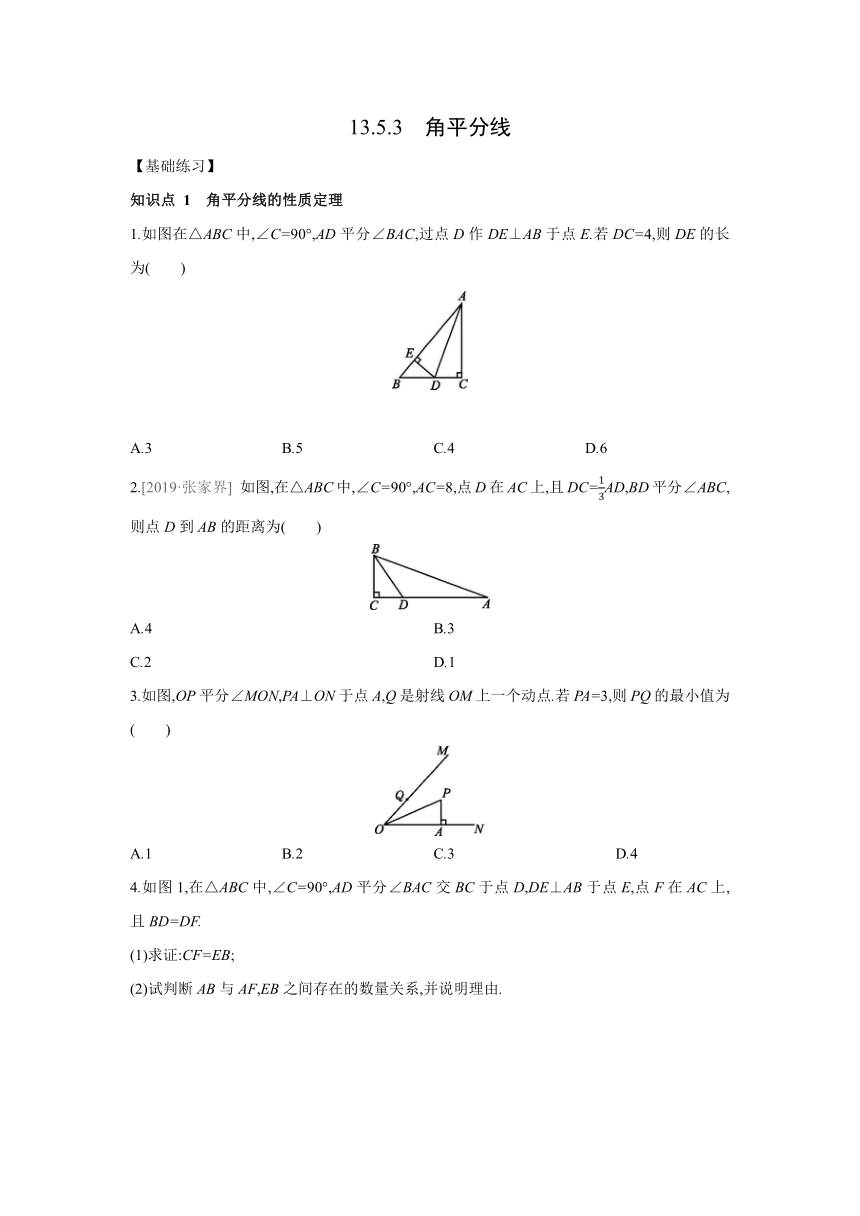
1.如图在△ABC中,∠C=90°,AD平分∠BAC,过点D作DE⊥AB于点E.若DC=4,则DE的长为( )
A.3
B.5
C.4
D.6
2.[2019·张家界]
如图,在△ABC中,∠C=90°,AC=8,点D在AC上,且DC=AD,BD平分∠ABC,则点D到AB的距离为( )
A.4
B.3
C.2
D.1
3.如图,OP平分∠MON,PA⊥ON于点A,Q是射线OM上一个动点.若PA=3,则PQ的最小值为( )
A.1
B.2
C.3
D.4
4.如图1,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,DE⊥AB于点E,点F在AC上,且BD=DF.
(1)求证:CF=EB;
(2)试判断AB与AF,EB之间存在的数量关系,并说明理由.
图1
知识点
2 角平分线性质定理的逆定理
5.如图2,已知∠CDA=∠CBA=90°,且CD=CB,则点C在∠ 的平分线上,点A在∠ 的平分线上.?
图2
6.如图3,PM=PN,∠BOC=30°,则∠AOB的度数为( )
图3
A.30°
B.45°
C.60°
D.50°
7.如图4,若点P到BE,BD,AC的距离恰好相等,则点P的位置:①在∠DBE的平分线上;②在∠DAC的平分线上;③在∠ECA的平分线上;④恰是∠DBE,∠DAC,∠ECA的平分线的交点.上述结论中,正确的有( )
图4
A.1个
B.2个
C.3个
D.4个
8.如图5所示,已知△ABC的角平分线BM,CN相交于点P.
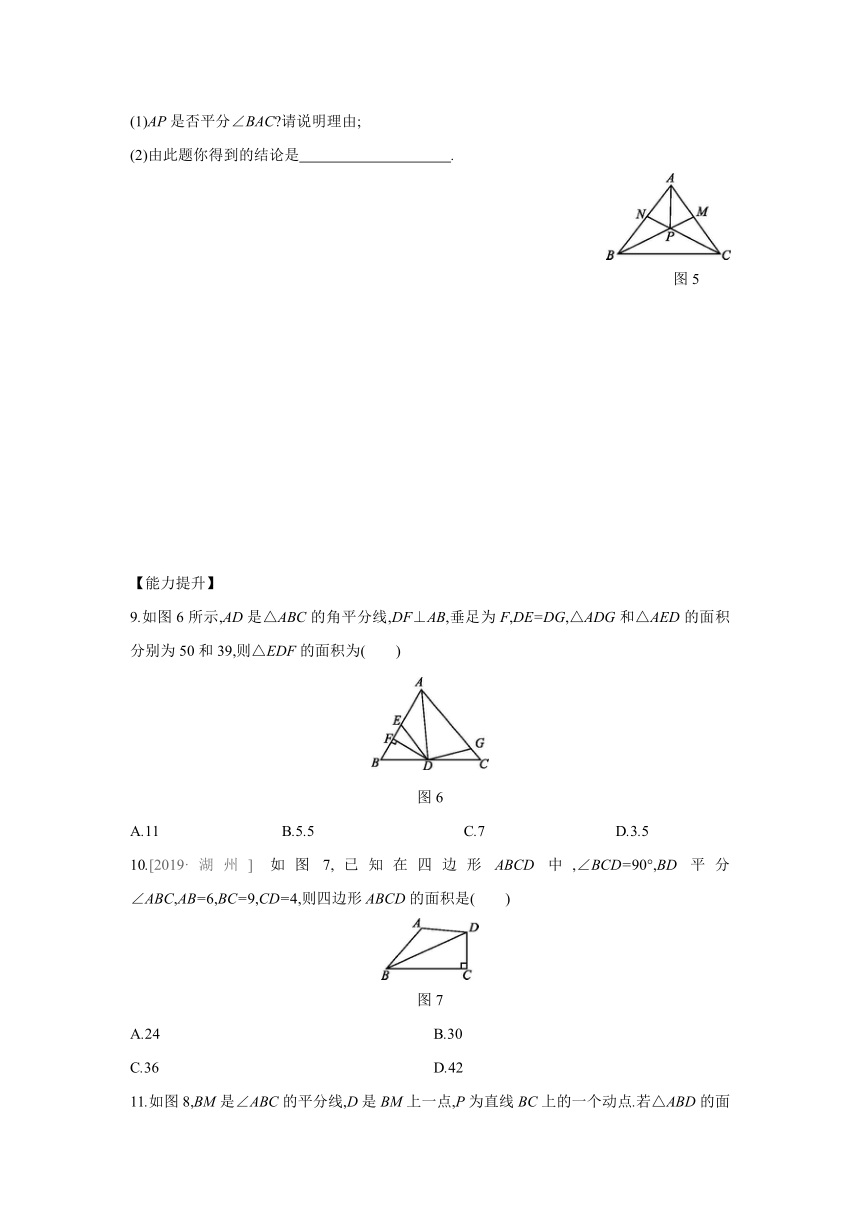
(1)AP是否平分∠BAC?请说明理由;
(2)由此题你得到的结论是
.?
图5
【能力提升】
9.如图6所示,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和39,则△EDF的面积为( )
图6
A.11
B.5.5
C.7
D.3.5
10.[2019·湖州]
如图7,已知在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD的面积是( )
图7
A.24
B.30
C.36
D.42
11.如图8,BM是∠ABC的平分线,D是BM上一点,P为直线BC上的一个动点.若△ABD的面积为9,AB=6,则线段DP的长不可能是( )
图8
A.2
B.3
C.4
D.5.5
12.如图9,已知OA和OB两条公路,以及C,D两个村庄,现要在∠AOB内部修建一个车站P,使车站到两个村庄的距离相等,即PC=PD,且P到OA,OB两条公路的距离相等,请在图中画出车站P的位置(要求尺规作图,不写作法,保留作图痕迹).
图9
13.如图10,D为锐角∠ABC内一点,点M在边BA上,点N在边BC上,且DM=DN,∠BMD+∠BND=180°.
求证:BD平分∠ABC.
图10
14.在△ABC中,AD,CE分别是∠BAC,∠ACB的平分线,AD,CE相交于点F.
(1)①如图11(a),若∠B=60°,∠ACB=90°,则∠AFC= °.?
②如图(b),若∠ACB不是直角,∠B=60°,则在①中所得的结论是否仍然成立?若成立,请证明;若不成立,请说明理由.
(2)在②的条件下,请猜想EF与DF的数量关系,并证明你的猜想.
图11
答案
1.C [解析]
∵∠C=90°,AD平分∠BAC,DE⊥AB于点E,∴DE=DC.∵DC=4,∴DE=4.故选C.
2.C [解析]
如图,过点D作DE⊥AB于点E.∵AC=8,DC=AD,∴DC=2.
∵∠C=90°,BD平分∠ABC,DE⊥AB,∴DE=DC=2,即点D到AB的距离为2.故选C.
3.C [解析]
如图,过点P作PB⊥OM于点B.
当点Q运动到点B时,PQ的值最小.∵OP平分∠MON,PA⊥ON,PA=3,∴PB=PA=3,
∴PQ的最小值为3.故选C.
4.解:(1)证明:∵AD是∠BAC的平分线,DE⊥AB,∠C=90°,
∴∠DEA=∠C=90°,DC=DE.
在Rt△FCD和Rt△BED中,
∵DC=DE,DF=DB,
∴Rt△FCD≌Rt△BED(H.L.),
∴CF=EB.
(2)AB=AF+2EB.理由:
在Rt△ACD和Rt△AED中,
∵DC=DE,AD=AD,
∴Rt△ACD≌Rt△AED(H.L.),
∴AC=AE,
∴AB=AE+EB=AC+EB=AF+CF+EB.
又∵CF=EB,∴AB=AF+2EB.
5.BAD BCD
6.C [解析]
∵点P在∠AOB的内部,PM⊥OA,PN⊥OB,PM=PN,∴点P在∠AOB的平分线上,∴OC平分∠AOB.∵∠BOC=30°,∴∠AOB=60°.故选C.
7.D
8.解:(1)AP平分∠BAC.理由如下:
如图,过点P作PQ⊥BC,PK⊥AB,PL⊥AC,
垂足分别为Q,K,L.
∵△ABC的角平分线BM,CN相交于点P,
∴PK=PQ,PL=PQ,∴PK=PL.
又∵PK⊥AB,PL⊥AC,
∴AP平分∠BAC.
(2)三角形的三条内角平分线相交于一点
9.B [解析]
过点D作DH⊥AG于点H,
则DH=DF,∴△ADF≌△ADH.
在Rt△EDF和Rt△GDH中,
∵DE=DG,DF=DH,
∴Rt△EDF≌Rt△GDH,
∴△ADG的面积-△ADE的面积=50-39=11=△EDF的面积×2,
∴△EDF的面积为5.5.
10.B [解析]
如图,过点D作DH⊥AB交BA的延长线于点H.
∵BD平分∠ABC,∠BCD=90°,∴DH=CD=4,
∴四边形ABCD的面积为S△ABD+S△BCD=AB·DH+BC·CD=×6×4+×9×4=30.故选B.
11.A [解析]
如图,过点D作DE⊥AB于点E,DF⊥BC于点F.∵△ABD的面积为9,AB=6,∴DE==3.∵BM是∠ABC的平分线,∴DF=DE=3,∴DP≥3.故选A.
12.解:如图,点P即为所求.
13.证明:如图,过点D作DP⊥AB,DQ⊥BC,垂足分别为P,Q.
∵∠BMD+∠BND=180°,∠BMD+∠PMD=180°,
∴∠BND=∠PMD.
在△DPM与△DQN中,
∵∠DPM=∠DQN=90°,∠PMD=∠QND,DM=DN,
∴△DPM
≌△DQN,
∴DP=DQ.
又∵点D在∠ABC内部,DP⊥AB,DQ⊥BC,
∴点D在∠ABC的平分线上,
即BD平分∠ABC.
14.解:(1)①∵∠B=60°,∠ACB=90°,
∴∠BAC=90°-60°=30°.
∵AD,CE分别是∠BAC,∠ACB的平分线,
∴∠FAC=∠BAC=×30°=15°,
∠FCA=∠ACB=×90°=45°,
∴∠AFC=180°-15°-45°=120°.
故答案为120.
②成立.
证明:∵AD,CE分别是∠BAC,∠ACB的平分线,
∴∠FAC+∠FCA=(∠BAC+∠ACB)=(180°-∠B),
∴∠AFC=180°-(∠FAC+∠FCA)=180°-(180°-∠B)=90°+∠B.
∵∠B=60°,∴∠AFC=90°+×60°=120°.
(2)EF=DF.
证明:如图,过点F作FG⊥BC于点G,FH⊥AB于点H,FM⊥AC于点M.
∵AD,CE分别是∠BAC,∠ACB的平分线,
∴FG=FM=FH.
∵∠EFH+∠DFH=∠EFD=∠AFC=120°,
∠DFG+∠DFH=360°-90°×2-60°=120°,
∴∠EFH=∠DFG.
在△EFH和△DFG中,
∵∠EHF=∠DGF=90°,FH=FG,∠EFH=∠DFG,∴△EFH≌△DFG(A.S.A.),
∴EF=DF.
【基础练习】
知识点
1 角平分线的性质定理
1.如图在△ABC中,∠C=90°,AD平分∠BAC,过点D作DE⊥AB于点E.若DC=4,则DE的长为( )
A.3
B.5
C.4
D.6
2.[2019·张家界]
如图,在△ABC中,∠C=90°,AC=8,点D在AC上,且DC=AD,BD平分∠ABC,则点D到AB的距离为( )
A.4
B.3
C.2
D.1
3.如图,OP平分∠MON,PA⊥ON于点A,Q是射线OM上一个动点.若PA=3,则PQ的最小值为( )
A.1
B.2
C.3
D.4
4.如图1,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,DE⊥AB于点E,点F在AC上,且BD=DF.
(1)求证:CF=EB;
(2)试判断AB与AF,EB之间存在的数量关系,并说明理由.
图1
知识点
2 角平分线性质定理的逆定理
5.如图2,已知∠CDA=∠CBA=90°,且CD=CB,则点C在∠ 的平分线上,点A在∠ 的平分线上.?
图2
6.如图3,PM=PN,∠BOC=30°,则∠AOB的度数为( )
图3
A.30°
B.45°
C.60°
D.50°
7.如图4,若点P到BE,BD,AC的距离恰好相等,则点P的位置:①在∠DBE的平分线上;②在∠DAC的平分线上;③在∠ECA的平分线上;④恰是∠DBE,∠DAC,∠ECA的平分线的交点.上述结论中,正确的有( )
图4
A.1个
B.2个
C.3个
D.4个
8.如图5所示,已知△ABC的角平分线BM,CN相交于点P.
(1)AP是否平分∠BAC?请说明理由;
(2)由此题你得到的结论是
.?
图5
【能力提升】
9.如图6所示,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和39,则△EDF的面积为( )
图6
A.11
B.5.5
C.7
D.3.5
10.[2019·湖州]
如图7,已知在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD的面积是( )
图7
A.24
B.30
C.36
D.42
11.如图8,BM是∠ABC的平分线,D是BM上一点,P为直线BC上的一个动点.若△ABD的面积为9,AB=6,则线段DP的长不可能是( )
图8
A.2
B.3
C.4
D.5.5
12.如图9,已知OA和OB两条公路,以及C,D两个村庄,现要在∠AOB内部修建一个车站P,使车站到两个村庄的距离相等,即PC=PD,且P到OA,OB两条公路的距离相等,请在图中画出车站P的位置(要求尺规作图,不写作法,保留作图痕迹).
图9
13.如图10,D为锐角∠ABC内一点,点M在边BA上,点N在边BC上,且DM=DN,∠BMD+∠BND=180°.
求证:BD平分∠ABC.
图10
14.在△ABC中,AD,CE分别是∠BAC,∠ACB的平分线,AD,CE相交于点F.
(1)①如图11(a),若∠B=60°,∠ACB=90°,则∠AFC= °.?
②如图(b),若∠ACB不是直角,∠B=60°,则在①中所得的结论是否仍然成立?若成立,请证明;若不成立,请说明理由.
(2)在②的条件下,请猜想EF与DF的数量关系,并证明你的猜想.
图11
答案
1.C [解析]
∵∠C=90°,AD平分∠BAC,DE⊥AB于点E,∴DE=DC.∵DC=4,∴DE=4.故选C.
2.C [解析]
如图,过点D作DE⊥AB于点E.∵AC=8,DC=AD,∴DC=2.
∵∠C=90°,BD平分∠ABC,DE⊥AB,∴DE=DC=2,即点D到AB的距离为2.故选C.
3.C [解析]
如图,过点P作PB⊥OM于点B.
当点Q运动到点B时,PQ的值最小.∵OP平分∠MON,PA⊥ON,PA=3,∴PB=PA=3,
∴PQ的最小值为3.故选C.
4.解:(1)证明:∵AD是∠BAC的平分线,DE⊥AB,∠C=90°,
∴∠DEA=∠C=90°,DC=DE.
在Rt△FCD和Rt△BED中,
∵DC=DE,DF=DB,
∴Rt△FCD≌Rt△BED(H.L.),
∴CF=EB.
(2)AB=AF+2EB.理由:
在Rt△ACD和Rt△AED中,
∵DC=DE,AD=AD,
∴Rt△ACD≌Rt△AED(H.L.),
∴AC=AE,
∴AB=AE+EB=AC+EB=AF+CF+EB.
又∵CF=EB,∴AB=AF+2EB.
5.BAD BCD
6.C [解析]
∵点P在∠AOB的内部,PM⊥OA,PN⊥OB,PM=PN,∴点P在∠AOB的平分线上,∴OC平分∠AOB.∵∠BOC=30°,∴∠AOB=60°.故选C.
7.D
8.解:(1)AP平分∠BAC.理由如下:
如图,过点P作PQ⊥BC,PK⊥AB,PL⊥AC,
垂足分别为Q,K,L.
∵△ABC的角平分线BM,CN相交于点P,
∴PK=PQ,PL=PQ,∴PK=PL.
又∵PK⊥AB,PL⊥AC,
∴AP平分∠BAC.
(2)三角形的三条内角平分线相交于一点
9.B [解析]
过点D作DH⊥AG于点H,
则DH=DF,∴△ADF≌△ADH.
在Rt△EDF和Rt△GDH中,
∵DE=DG,DF=DH,
∴Rt△EDF≌Rt△GDH,
∴△ADG的面积-△ADE的面积=50-39=11=△EDF的面积×2,
∴△EDF的面积为5.5.
10.B [解析]
如图,过点D作DH⊥AB交BA的延长线于点H.
∵BD平分∠ABC,∠BCD=90°,∴DH=CD=4,
∴四边形ABCD的面积为S△ABD+S△BCD=AB·DH+BC·CD=×6×4+×9×4=30.故选B.
11.A [解析]
如图,过点D作DE⊥AB于点E,DF⊥BC于点F.∵△ABD的面积为9,AB=6,∴DE==3.∵BM是∠ABC的平分线,∴DF=DE=3,∴DP≥3.故选A.
12.解:如图,点P即为所求.
13.证明:如图,过点D作DP⊥AB,DQ⊥BC,垂足分别为P,Q.
∵∠BMD+∠BND=180°,∠BMD+∠PMD=180°,
∴∠BND=∠PMD.
在△DPM与△DQN中,
∵∠DPM=∠DQN=90°,∠PMD=∠QND,DM=DN,
∴△DPM
≌△DQN,
∴DP=DQ.
又∵点D在∠ABC内部,DP⊥AB,DQ⊥BC,
∴点D在∠ABC的平分线上,
即BD平分∠ABC.
14.解:(1)①∵∠B=60°,∠ACB=90°,
∴∠BAC=90°-60°=30°.
∵AD,CE分别是∠BAC,∠ACB的平分线,
∴∠FAC=∠BAC=×30°=15°,
∠FCA=∠ACB=×90°=45°,
∴∠AFC=180°-15°-45°=120°.
故答案为120.
②成立.
证明:∵AD,CE分别是∠BAC,∠ACB的平分线,
∴∠FAC+∠FCA=(∠BAC+∠ACB)=(180°-∠B),
∴∠AFC=180°-(∠FAC+∠FCA)=180°-(180°-∠B)=90°+∠B.
∵∠B=60°,∴∠AFC=90°+×60°=120°.
(2)EF=DF.
证明:如图,过点F作FG⊥BC于点G,FH⊥AB于点H,FM⊥AC于点M.
∵AD,CE分别是∠BAC,∠ACB的平分线,
∴FG=FM=FH.
∵∠EFH+∠DFH=∠EFD=∠AFC=120°,
∠DFG+∠DFH=360°-90°×2-60°=120°,
∴∠EFH=∠DFG.
在△EFH和△DFG中,
∵∠EHF=∠DGF=90°,FH=FG,∠EFH=∠DFG,∴△EFH≌△DFG(A.S.A.),
∴EF=DF.
