2021-2022学年华东师大版数学九年级上册23.2 相似图形同步练习(word解析版)
文档属性
| 名称 | 2021-2022学年华东师大版数学九年级上册23.2 相似图形同步练习(word解析版) |

|
|
| 格式 | docx | ||
| 文件大小 | 302.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-31 00:00:00 | ||
图片预览




文档简介
23.2
相似图形
一、单选题
1.下列图形中不一定相似的是(
)
A.两个矩形
B.两个圆
C.两个正方形
D.两个等边三角形
2.如图,在矩形中,点E、F分别在,上,四边形是正方形,矩形矩形,,则的值为(
)
A.
B.
C.
D.
3.用一个2倍放大镜照一个,下面说法中错误的是(
)
A.放大后,是原来的2倍
B.放大后,各边长是原来的2倍
C.放大后,周长是原来的2倍
D.放大后,面积是原来的4倍
4.在长8cm,宽6cm的矩形ABCD中,截去一个矩形后,使留下的矩形BEFA与原矩形ABCD相似,那么留下的矩形BEFA面积为(
)cm2
A.24
B.25
C.26
D.27
5.下列命题中,是真命题的有(
)
(1)两条线段长度的比叫做两条线段的比;
(2)两个矩形一定是相似形;
(3)任意两个相似多边形,它们的对应角相等,对应边也相等;
(4)若线段a与b的比是3:5,则a=3,b=5.
A.1个
B.2个
C.3个
D.4个
6.如图,四边形ABCD∽四边形EFGH,∠A=80°,∠C=90°,∠F=70°,则∠E的度数为(
)
A.70°
B.80°
C.90°
D.120°
7.如图,取一张长为a,宽为b的长方形纸片,将它对折两次后得到一张小长方形纸片,若要使小长方形与原长方形相似,则原长方形纸片的边a、b应满足的条件是(
)
A.a=b
B.a=2b
C.a=2b
D.a=4b
8.如图,细线平行于正多边形一边,并把它分割成两部分,则阴影部分多边形与原多边形相似的是(
)
A.
B.
C.
D.
9.下列各组中的图形,不是相似图形的是(
)
A.同一座城市的两张比例尺不同的地图;
B.一个人现在的照片和他十年前的照片;
C.两个正方形;
D.国旗上的五角星.
10.如图,把一个长方形按如图方式划分成三个全等的小长方形,每一个小长方形与原长方形相似,若原长方形的宽为4,则小长方形的宽为(
)
A.
B.
C.
D.
11.将一张矩形纸片对折后裁下,得到两张大小完全一样的矩形纸片,已知它们都与原来的矩形相似,那么原来矩形长与宽的比为(
)
A.2:1
B.:1
C.3:1
D.:1
12.将矩形按照如图所示的方式向外扩张得到新矩形,每条对角线向其延长线两个方向各延伸,若所得新矩形与原矩形相似,则的值的个数可以是(
)
A.1
B.2
C.3
D.无数个
二、填空题
13.相似的两个图形,它们的大小_________(填“一定”,“不一定”,“一定不”)相同.
14.与是两个相似三角形,,,,则的度数可以是______.
15.若两个相似多边形的最长边的长度分别为10和20,且其中一个多边形的最短边长为4,则另一个多边形的最短边长为_________.
16.下列五组图形中,①两个等腰三角形;②两个等边三形;③两个菱形;④两个矩形;⑤两个正方形.一定相似的有_______(填序号)
17.已知一个矩形的两邻边长之比为1:,一条平行于边的直线将该矩形分为两个小矩形,如果所得两小矩形相似,那么这两个小矩形的相似比为________.
三、解答题
18.如图,四边形ABCD∽四边形A′B′C′D′,求边x、y的长度和角α的大小.
19.设四边形与四边形是相似的图形,且与、与、与是对应点,已知,,求四边形的周长.
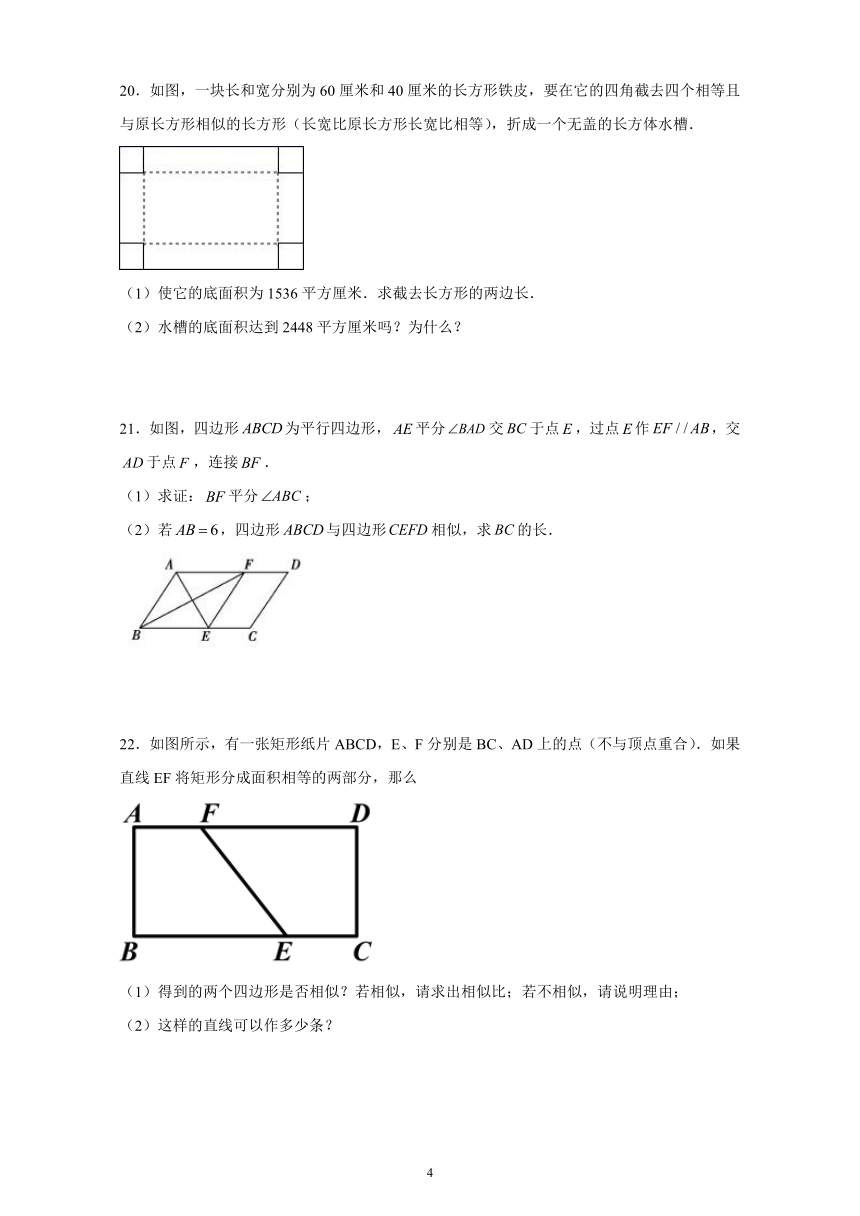
20.如图,一块长和宽分别为60厘米和40厘米的长方形铁皮,要在它的四角截去四个相等且与原长方形相似的长方形(长宽比原长方形长宽比相等),折成一个无盖的长方体水槽.
(1)使它的底面积为1536平方厘米.求截去长方形的两边长.
(2)水槽的底面积达到2448平方厘米吗?为什么?
21.如图,四边形为平行四边形,平分交于点,过点作,交于点,连接.
(1)求证:平分;
(2)若,四边形与四边形相似,求的长.
22.如图所示,有一张矩形纸片ABCD,E、F分别是BC、AD上的点(不与顶点重合).如果直线EF将矩形分成面积相等的两部分,那么
(1)得到的两个四边形是否相似?若相似,请求出相似比;若不相似,请说明理由;
(2)这样的直线可以作多少条?
参考答案
1.A
解:A、两个矩形不一定相似,由于对应边不一定成比例,故符合题意;
B、两个圆一定相似,故不满足题意;
C、根据两个图形相似的定义,两个正方形相似,故不满足题意;
D、根据两个图形相似的定义,两个等边三角形相似,故不满足题意;
故选:A.
2.A
解:矩形矩形,
,设正方形的边长为,,
则,
,
,
,,
,
,
,
,
故选:A.
3.A
解:因为放大前后的三角形相似,
放大后三角形的内角度数不变,
面积为原来的4倍,周长和边长均为原来的2倍,
故选A.
4.D
解:
矩形BEFA与矩形ABCD相似,
故选:
5.A
解:(1)两条线段长度的比叫做两条线段的比,是真命题;
(2)两个矩形不一定相似,因为对应边的比值不一定相等,不是真命题;
(3)任意两个相似多边形,它们的对应角相等,对应边成比例,不是真命题;
(4)若线段a与b的比是3:5,但a不一定是3,b不一定是5,不是真命题;
综上,只有(1)是真命题,共1个.
故选:A.
6.B
解:∵四边形ABCD∽四边形EFGH,∠A=80°,
∴∠E=∠A=80°,
故选:B
7.B
解:对折两次后的小长方形的长为b,宽为,
要使小长方形与原长方形相似,只要满足即可,
∴.
故选:B.
8.A
解:A、阴影三角形与原三角形的对应角相等、对应边的比相等,符合相似多边形的定义,符合题意;
B、阴影矩形与原矩形的对应角相等,但对应边的比不相等,不符合相似多边形的定义,不符合题意;
C、阴影五边形与原五边形的对应角相等,但对应边的比不相等,不符合相似多边形的定义,不符合题意;
D、阴影六边形与原六边形的对应角相等,但对应边的比不相等,不符合相似多边形的定义,不符合题意;
故选:A.
9.B
解:A、同一座城市的两张比例尺不同的地图是相似的,故不符合题意;
B、一个人现在的照片和他十年前的照片不相似,故符合题意;
C、两个正方形是相似的,故不符合题意;
D、国旗上的五角星是相似的,故不符合题意;
故选B.
10.A
解:∵每一个小长方形与原长方形相似,小长方形的宽为x
∴
解得,x=或x=-
(舍去),
故选:A
11.B
解:设原矩形长2a,宽b,则对折后的矩形的长为b,宽为a,
∵对折后的矩形与原矩形相似,
∴,
∴,
∴,
∴.
故选B.
12.D
解:新矩形与原矩形相似,因此可得到对应边成比例,对应角相等,与a的取值无关,
故选:D.
13.不一定
解:相似的两个图形形状相同,但大小不一定相等,只有两个图形全等时大小才相等,全等是相似的一种特殊情况.
故答案为:不一定.
14.或
解:易得∠C=60°,与∠D是对应角.则①当∠E与∠A是对应角时,∵∠A=50°,
∴∠E=50°,
②当∠E与∠B是对应角时,∵∠B=70°,
∴∠E=70°,
综上,∠E的度数为50°或70°,
故答案为或.
15.2或8
解:设最短边为x,由题意得,
10:20=4:x,或10:20=x:4,
∴x=8或2.
故答案为:
2或8.
16.②⑤
解:两个等腰三角形的顶角不一定相等,故不一定相似;
两个等边三角形一定相似;
两个菱形的内角不一定相等,故不一定相似;
两个矩形的相邻边长比例不一定相等,故不一定相似;
两个正方形一定相似;
故答案为:②⑤.
17.1或或2
解:如图所示,矩形ABCD中,AB:AD=1:,
∴AD=BC
若直线l∥AD,交AB、CD于E、F
根据题意和图形可知:矩形AEFD∽矩形BEFC
此时这两个小矩形的相似比为AD:BC=1;
根据相似图形的性质,两个相似图形中长边必定对应长边,故此时不存在其它情况;
若直线l∥AB,交AD、BC于E、F
此时存在两种情况:①若矩形ABFE∽矩形DCFE,如下图所示
此时这两个小矩形的相似比为AB:DC=1;
②若矩形BAEF∽矩形EDCF,如下图所示
∴
设AB=CD=a,AE=x,则AD=,DE=
∴
解得:x=或x=
当x=时,这两个小矩形的相似比为AE:CD=:a=;
当x=时,这两个小矩形的相似比为AE:CD=:a=2;
综上:这两个小矩形的相似比为1或或2.
故答案为:1或或2.
18.x=12,,α=83°.
解:∵四边形ABCD∽四边形A′B′C′D′,
∴,即,∠C=α,∠D=∠D′=140°.
∴x=12,,α=∠C=360°﹣∠A﹣∠B﹣∠D=360°﹣62°﹣75°﹣140°=83°.
19.38
解:∵四边形ABCD与四边形A1B1C1D1是相似的图形,
∴,
又∵AB=12,BC=18,CD=18,AD=9,A1B1=8,
∴,
∴B1C1=12,C1D1=12,D1A1=6,
∴四边形A1B1C1D1的周长=8+12+12+6=38.
20.(1)长为6厘米,宽为4厘米;(2)不能,理由见解析
解:(1)设截去长方形的长为3x厘米,
∵截去的长方形与原长方形相似,
则截去长方形的宽为2x厘米,
∴底面积为,
解得:x=2或18(舍),
∴3x=6,2x=4,
∴截去长方形的长为6厘米,宽为4厘米;
(2)由题意可得:
,
解得:x=或,
∵=<0,故不符合;
>,故不符合,
∴底面积不能达到2448平方厘米.
21.(1)见解析;(2)
(1)证明:∵四边形是平行四边形,
,
又,
∴四边形是平行四边形.
由,
得.
平分
,
∴四边形是菱形,
平分.
(2)解:由(1)知,四边形为菱形,
.
∵四边形与四边形相似,
,
即,
或BC=(不符合实际,故舍去).
22.见解析
解:(1)相似.理由如下:
因为EF将矩形ABCD分成面积相等的两部分,所以可设AB=a,AD=b,BE=x.
于是有,
所以x+AF=b-x+b-AF,即AF=b-x.
又EC=b-x,所以AF=EC.
在矩形ABCD中,AB=CD,AD=BC,AD∥BC,
所以DF=BE,∠AFE=∠FEC,∠DFE=∠BEF,∠A=∠B=∠C=∠D=90°.
所以在四边形ABEF与四边形CDFE中,有
∠A=∠C=90°,∠B=∠D=90°,∠AFE=∠FEC,∠BEF=∠DFE,
,
所以四边形ABEF与四边形CDFE相似,相似比为1.
(2)这样的直线有无数条,只要过矩形对角线的交点且满足条件即可.
相似图形
一、单选题
1.下列图形中不一定相似的是(
)
A.两个矩形
B.两个圆
C.两个正方形
D.两个等边三角形
2.如图,在矩形中,点E、F分别在,上,四边形是正方形,矩形矩形,,则的值为(
)
A.
B.
C.
D.
3.用一个2倍放大镜照一个,下面说法中错误的是(
)
A.放大后,是原来的2倍
B.放大后,各边长是原来的2倍
C.放大后,周长是原来的2倍
D.放大后,面积是原来的4倍
4.在长8cm,宽6cm的矩形ABCD中,截去一个矩形后,使留下的矩形BEFA与原矩形ABCD相似,那么留下的矩形BEFA面积为(
)cm2
A.24
B.25
C.26
D.27
5.下列命题中,是真命题的有(
)
(1)两条线段长度的比叫做两条线段的比;
(2)两个矩形一定是相似形;
(3)任意两个相似多边形,它们的对应角相等,对应边也相等;
(4)若线段a与b的比是3:5,则a=3,b=5.
A.1个
B.2个
C.3个
D.4个
6.如图,四边形ABCD∽四边形EFGH,∠A=80°,∠C=90°,∠F=70°,则∠E的度数为(
)
A.70°
B.80°
C.90°
D.120°
7.如图,取一张长为a,宽为b的长方形纸片,将它对折两次后得到一张小长方形纸片,若要使小长方形与原长方形相似,则原长方形纸片的边a、b应满足的条件是(
)
A.a=b
B.a=2b
C.a=2b
D.a=4b
8.如图,细线平行于正多边形一边,并把它分割成两部分,则阴影部分多边形与原多边形相似的是(
)
A.
B.
C.
D.
9.下列各组中的图形,不是相似图形的是(
)
A.同一座城市的两张比例尺不同的地图;
B.一个人现在的照片和他十年前的照片;
C.两个正方形;
D.国旗上的五角星.
10.如图,把一个长方形按如图方式划分成三个全等的小长方形,每一个小长方形与原长方形相似,若原长方形的宽为4,则小长方形的宽为(
)
A.
B.
C.
D.
11.将一张矩形纸片对折后裁下,得到两张大小完全一样的矩形纸片,已知它们都与原来的矩形相似,那么原来矩形长与宽的比为(
)
A.2:1
B.:1
C.3:1
D.:1
12.将矩形按照如图所示的方式向外扩张得到新矩形,每条对角线向其延长线两个方向各延伸,若所得新矩形与原矩形相似,则的值的个数可以是(
)
A.1
B.2
C.3
D.无数个
二、填空题
13.相似的两个图形,它们的大小_________(填“一定”,“不一定”,“一定不”)相同.
14.与是两个相似三角形,,,,则的度数可以是______.
15.若两个相似多边形的最长边的长度分别为10和20,且其中一个多边形的最短边长为4,则另一个多边形的最短边长为_________.
16.下列五组图形中,①两个等腰三角形;②两个等边三形;③两个菱形;④两个矩形;⑤两个正方形.一定相似的有_______(填序号)
17.已知一个矩形的两邻边长之比为1:,一条平行于边的直线将该矩形分为两个小矩形,如果所得两小矩形相似,那么这两个小矩形的相似比为________.
三、解答题
18.如图,四边形ABCD∽四边形A′B′C′D′,求边x、y的长度和角α的大小.
19.设四边形与四边形是相似的图形,且与、与、与是对应点,已知,,求四边形的周长.
20.如图,一块长和宽分别为60厘米和40厘米的长方形铁皮,要在它的四角截去四个相等且与原长方形相似的长方形(长宽比原长方形长宽比相等),折成一个无盖的长方体水槽.
(1)使它的底面积为1536平方厘米.求截去长方形的两边长.
(2)水槽的底面积达到2448平方厘米吗?为什么?
21.如图,四边形为平行四边形,平分交于点,过点作,交于点,连接.
(1)求证:平分;
(2)若,四边形与四边形相似,求的长.
22.如图所示,有一张矩形纸片ABCD,E、F分别是BC、AD上的点(不与顶点重合).如果直线EF将矩形分成面积相等的两部分,那么
(1)得到的两个四边形是否相似?若相似,请求出相似比;若不相似,请说明理由;
(2)这样的直线可以作多少条?
参考答案
1.A
解:A、两个矩形不一定相似,由于对应边不一定成比例,故符合题意;
B、两个圆一定相似,故不满足题意;
C、根据两个图形相似的定义,两个正方形相似,故不满足题意;
D、根据两个图形相似的定义,两个等边三角形相似,故不满足题意;
故选:A.
2.A
解:矩形矩形,
,设正方形的边长为,,
则,
,
,
,,
,
,
,
,
故选:A.
3.A
解:因为放大前后的三角形相似,
放大后三角形的内角度数不变,
面积为原来的4倍,周长和边长均为原来的2倍,
故选A.
4.D
解:
矩形BEFA与矩形ABCD相似,
故选:
5.A
解:(1)两条线段长度的比叫做两条线段的比,是真命题;
(2)两个矩形不一定相似,因为对应边的比值不一定相等,不是真命题;
(3)任意两个相似多边形,它们的对应角相等,对应边成比例,不是真命题;
(4)若线段a与b的比是3:5,但a不一定是3,b不一定是5,不是真命题;
综上,只有(1)是真命题,共1个.
故选:A.
6.B
解:∵四边形ABCD∽四边形EFGH,∠A=80°,
∴∠E=∠A=80°,
故选:B
7.B
解:对折两次后的小长方形的长为b,宽为,
要使小长方形与原长方形相似,只要满足即可,
∴.
故选:B.
8.A
解:A、阴影三角形与原三角形的对应角相等、对应边的比相等,符合相似多边形的定义,符合题意;
B、阴影矩形与原矩形的对应角相等,但对应边的比不相等,不符合相似多边形的定义,不符合题意;
C、阴影五边形与原五边形的对应角相等,但对应边的比不相等,不符合相似多边形的定义,不符合题意;
D、阴影六边形与原六边形的对应角相等,但对应边的比不相等,不符合相似多边形的定义,不符合题意;
故选:A.
9.B
解:A、同一座城市的两张比例尺不同的地图是相似的,故不符合题意;
B、一个人现在的照片和他十年前的照片不相似,故符合题意;
C、两个正方形是相似的,故不符合题意;
D、国旗上的五角星是相似的,故不符合题意;
故选B.
10.A
解:∵每一个小长方形与原长方形相似,小长方形的宽为x
∴
解得,x=或x=-
(舍去),
故选:A
11.B
解:设原矩形长2a,宽b,则对折后的矩形的长为b,宽为a,
∵对折后的矩形与原矩形相似,
∴,
∴,
∴,
∴.
故选B.
12.D
解:新矩形与原矩形相似,因此可得到对应边成比例,对应角相等,与a的取值无关,
故选:D.
13.不一定
解:相似的两个图形形状相同,但大小不一定相等,只有两个图形全等时大小才相等,全等是相似的一种特殊情况.
故答案为:不一定.
14.或
解:易得∠C=60°,与∠D是对应角.则①当∠E与∠A是对应角时,∵∠A=50°,
∴∠E=50°,
②当∠E与∠B是对应角时,∵∠B=70°,
∴∠E=70°,
综上,∠E的度数为50°或70°,
故答案为或.
15.2或8
解:设最短边为x,由题意得,
10:20=4:x,或10:20=x:4,
∴x=8或2.
故答案为:
2或8.
16.②⑤
解:两个等腰三角形的顶角不一定相等,故不一定相似;
两个等边三角形一定相似;
两个菱形的内角不一定相等,故不一定相似;
两个矩形的相邻边长比例不一定相等,故不一定相似;
两个正方形一定相似;
故答案为:②⑤.
17.1或或2
解:如图所示,矩形ABCD中,AB:AD=1:,
∴AD=BC
若直线l∥AD,交AB、CD于E、F
根据题意和图形可知:矩形AEFD∽矩形BEFC
此时这两个小矩形的相似比为AD:BC=1;
根据相似图形的性质,两个相似图形中长边必定对应长边,故此时不存在其它情况;
若直线l∥AB,交AD、BC于E、F
此时存在两种情况:①若矩形ABFE∽矩形DCFE,如下图所示
此时这两个小矩形的相似比为AB:DC=1;
②若矩形BAEF∽矩形EDCF,如下图所示
∴
设AB=CD=a,AE=x,则AD=,DE=
∴
解得:x=或x=
当x=时,这两个小矩形的相似比为AE:CD=:a=;
当x=时,这两个小矩形的相似比为AE:CD=:a=2;
综上:这两个小矩形的相似比为1或或2.
故答案为:1或或2.
18.x=12,,α=83°.
解:∵四边形ABCD∽四边形A′B′C′D′,
∴,即,∠C=α,∠D=∠D′=140°.
∴x=12,,α=∠C=360°﹣∠A﹣∠B﹣∠D=360°﹣62°﹣75°﹣140°=83°.
19.38
解:∵四边形ABCD与四边形A1B1C1D1是相似的图形,
∴,
又∵AB=12,BC=18,CD=18,AD=9,A1B1=8,
∴,
∴B1C1=12,C1D1=12,D1A1=6,
∴四边形A1B1C1D1的周长=8+12+12+6=38.
20.(1)长为6厘米,宽为4厘米;(2)不能,理由见解析
解:(1)设截去长方形的长为3x厘米,
∵截去的长方形与原长方形相似,
则截去长方形的宽为2x厘米,
∴底面积为,
解得:x=2或18(舍),
∴3x=6,2x=4,
∴截去长方形的长为6厘米,宽为4厘米;
(2)由题意可得:
,
解得:x=或,
∵=<0,故不符合;
>,故不符合,
∴底面积不能达到2448平方厘米.
21.(1)见解析;(2)
(1)证明:∵四边形是平行四边形,
,
又,
∴四边形是平行四边形.
由,
得.
平分
,
∴四边形是菱形,
平分.
(2)解:由(1)知,四边形为菱形,
.
∵四边形与四边形相似,
,
即,
或BC=(不符合实际,故舍去).
22.见解析
解:(1)相似.理由如下:
因为EF将矩形ABCD分成面积相等的两部分,所以可设AB=a,AD=b,BE=x.
于是有,
所以x+AF=b-x+b-AF,即AF=b-x.
又EC=b-x,所以AF=EC.
在矩形ABCD中,AB=CD,AD=BC,AD∥BC,
所以DF=BE,∠AFE=∠FEC,∠DFE=∠BEF,∠A=∠B=∠C=∠D=90°.
所以在四边形ABEF与四边形CDFE中,有
∠A=∠C=90°,∠B=∠D=90°,∠AFE=∠FEC,∠BEF=∠DFE,
,
所以四边形ABEF与四边形CDFE相似,相似比为1.
(2)这样的直线有无数条,只要过矩形对角线的交点且满足条件即可.
