23.3.3 相似三角形的性质 同步练习 2021-2022学年华东师大版数学九年级上册(word版含答案)
文档属性
| 名称 | 23.3.3 相似三角形的性质 同步练习 2021-2022学年华东师大版数学九年级上册(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 609.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-31 08:03:30 | ||
图片预览


文档简介
23.3.3
相似三角形的性质
一、单选题
1.已知,且,,,,则的周长为(
)
A.
B.
C.
D.
2.如图,在中,,且,则的值为(
)
A.
B.
C.
D.
3.如图,数学兴趣小组利用硬纸板自制的Rt△ABC来测量操场旗杆MN的高度,他们通过调整测量位置,并使边AC与旗杆顶点M在同一直线上,已知AC=0.8米,BC=0.5米,目测点A到地面的距离AD=1.5米,到旗杆的水平距离AE=20米,则旗杆MN的高度为(
)
A.12米
B.12.5米
C.14米
D.15米
4.如图,在中,,则的长是(
).
A.
B.6
C.
D.
5.如图所示,在中,,,在中,,点P在上,交于点E,交于点F.当时,的值为(
).
A.1
B.2
C.3
D.4
6.如图所示,O为四边形的边的中点,,则的长是(
).
A.
B.6
C.
D.17
7.如图,将矩形沿直线折叠,顶点D恰好落在边上的F处.已知,则(
)
A.13
B.12
C.11
D.10
8.如图,在正方形中,E为的中点,G,F分别为,边上的点.若,则的长为(
).
A.2
B.5
C.
D.
9.如图,在中,,则的长为(
).
A.
B.8
C.10
D.16
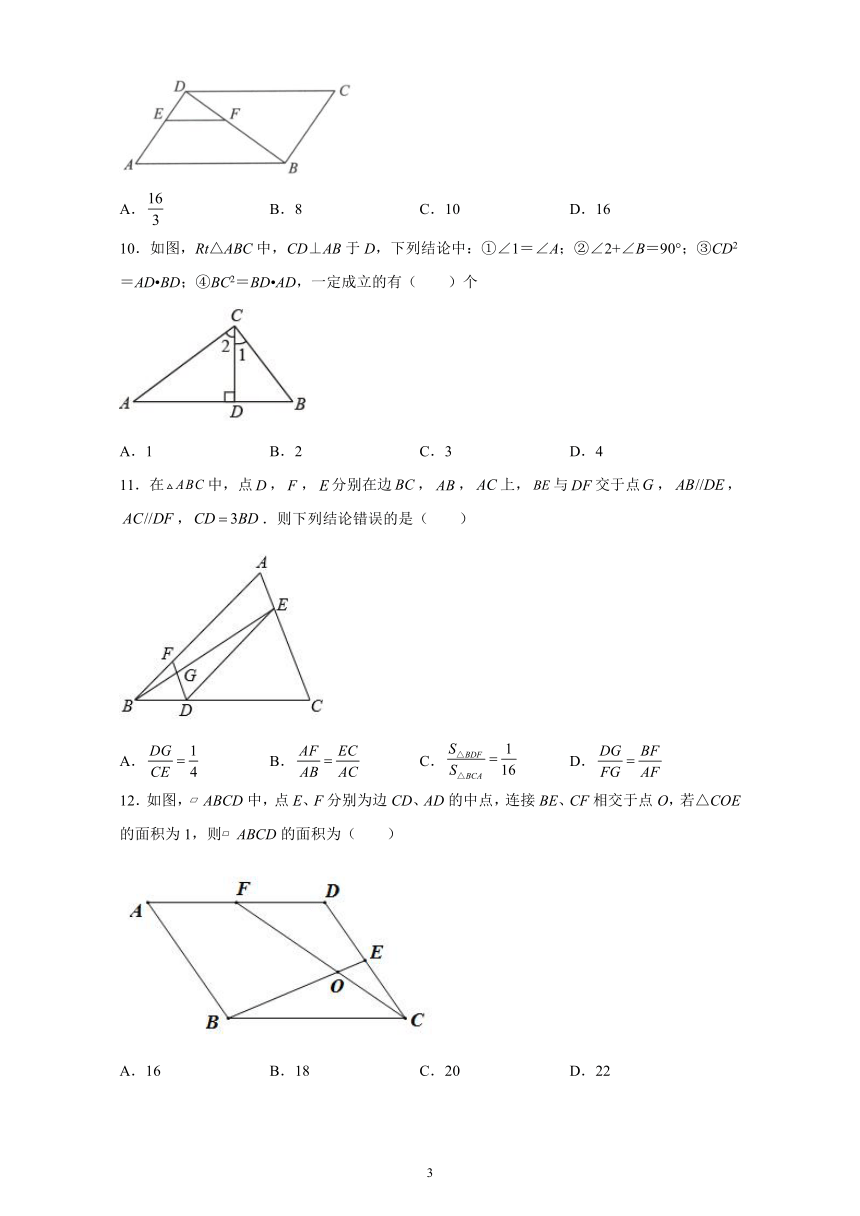
10.如图,Rt△ABC中,CD⊥AB于D,下列结论中:①∠1=∠A;②∠2+∠B=90°;③CD2=AD?BD;④BC2=BD?AD,一定成立的有(
)个
A.1
B.2
C.3
D.4
11.在中,点,,分别在边,,上,与交于点,,,.则下列结论错误的是(
)
A.
B.
C.
D.
12.如图,?ABCD中,点E、F分别为边CD、AD的中点,连接BE、CF相交于点O,若△COE的面积为1,则?ABCD的面积为(
)
A.16
B.18
C.20
D.22
二、填空题
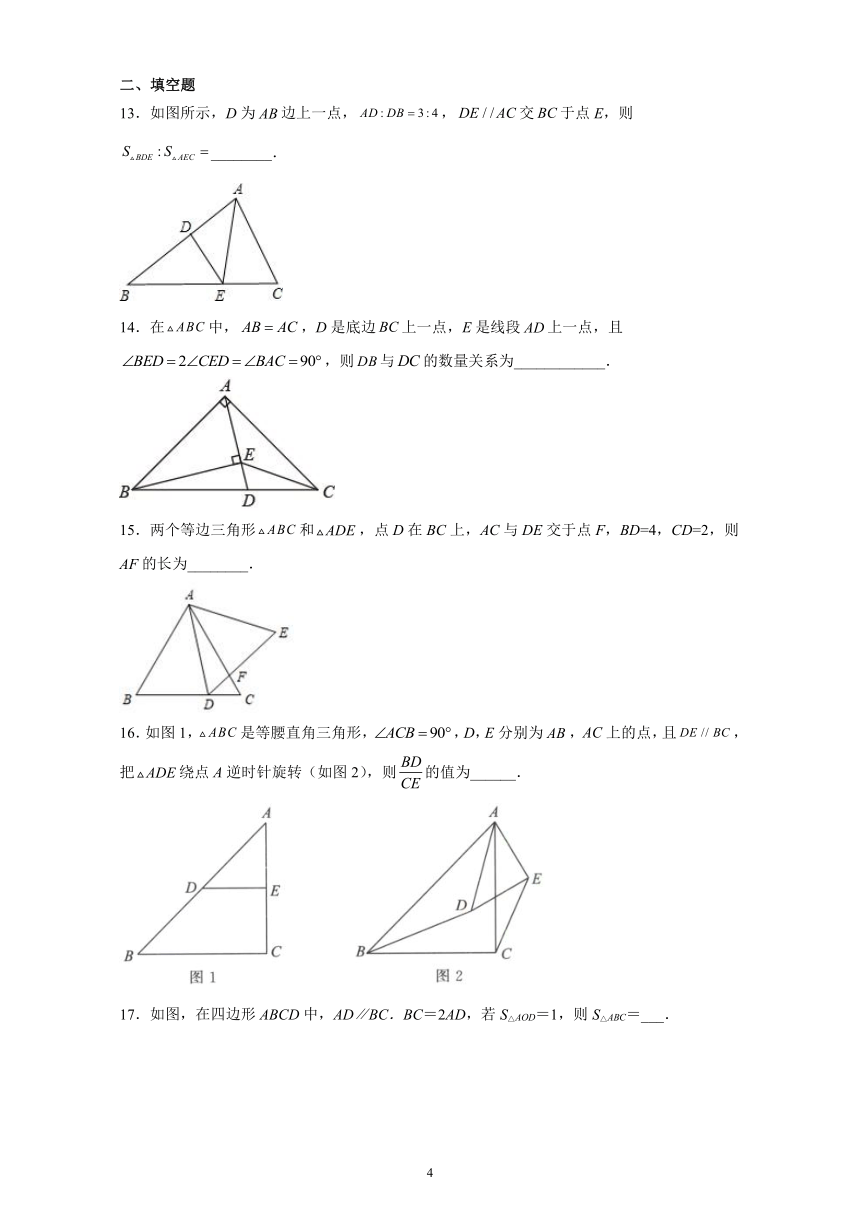
13.如图所示,D为边上一点,,交于点E,则________.
14.在中,,D是底边上一点,E是线段上一点,且,则与的数量关系为____________.
15.两个等边三角形和,点D在BC上,AC与DE交于点F,BD=4,CD=2,则AF的长为________.
16.如图1,是等腰直角三角形,,D,E分别为,上的点,且,把绕点A逆时针旋转(如图2),则的值为______.
17.如图,在四边形ABCD中,AD∥BC.BC=2AD,若S△AOD=1,则S△ABC=___.
三、解答题
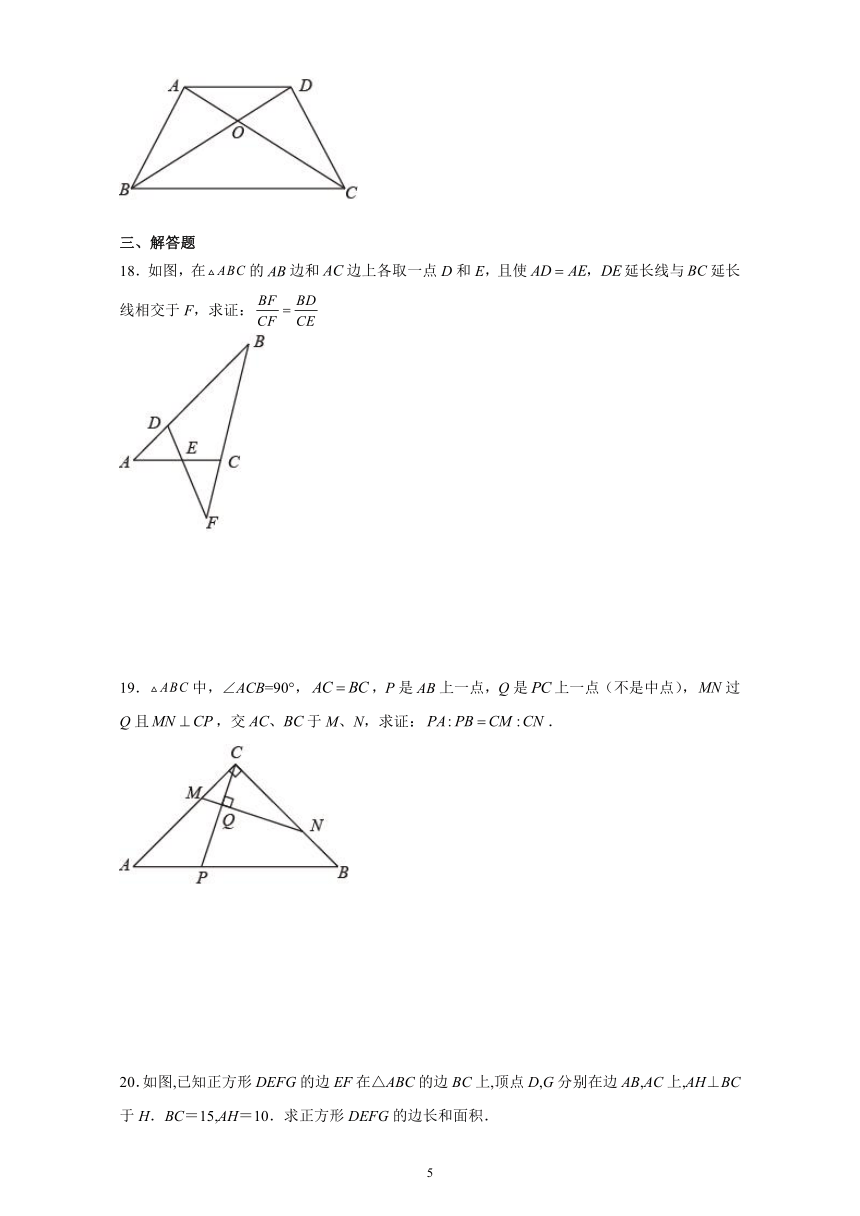
18.如图,在的边和边上各取一点D和E,且使延长线与延长线相交于F,求证:
19.中,∠ACB=90°,,P是上一点,Q是上一点(不是中点),过Q且,交于M、N,求证:.
20.如图,已知正方形DEFG的边EF在△ABC的边BC上,顶点D,G分别在边AB,AC上,AH⊥BC于H.BC=15,AH=10.求正方形DEFG的边长和面积.
21.如图,矩形OABC中,AO=4,AB=8,点E,F分别在边AB,OC上,且AE=3,将矩形的部分沿直线EF翻折,点A的对应点A'恰好落在对角线AC上,求OF的长.
22.如图,是的角平分线,延长至,连结,使.
(1)求证:;
(2)若,,求的长.
参考答案
1.A
解:∵△ABC∽△A′B′C′,
∴△A′B′C′的周长
∶△ABC的周长=A′C′:AC,
∵A′C′=3cm,BC=5cm,AC=4cm,AB=7cm,
∴△A′B′C′的周长∶(5+4+7)=3:4,
∴△A′B′C′的周长为12cm,
故选:A.
2.A
解:∵
∴
∴
∴
∴
故选A
3.C
解:由题意可知:,
∴四边形为矩形
∴
又∵
∴
∴
∴
故答案为C.
4.B
解:∵如图,在Rt△ABC中,∠C=90°,CD⊥AB,
∴∠A+∠ACD=∠ACD+∠BCD=90°,
∴∠A=∠BCD,
又∵∠ADC=∠CDB=90°,
∴,
∴,
∴CD2=BD?AD=9×4=36,
∴CD=6(舍去负值).
故选:B.
5.C
解:∵在中,,,
∴AC=
,
过P作PH⊥BC于H,PQ⊥AB于Q,
则∠PQB=∠PHB=∠B=90°,
∴四边形PQBH是矩形,
∴PH=BQ,∠QPH=90°=∠MPN,PQ∥BC,
∴∠EPH+∠QPE=∠EPH+∠HPF=90°,
∴∠QPE=∠HPF,
∴△PQE∽△PHF,
∴,又PE=2PF,
∴PQ=2PH=2BQ,
∵PQ∥BC,
∴△AQP∽△ABC,
∴,
设BQ=x,则AQ=3﹣x,PQ=2x,
∴,
解得:,AP=3,
故选:C.
6.C
解:∵,∠B+∠BCO=∠AOC=∠DOC+∠AOD,
∴∠BCO=∠AOD,
又∵,
∴,
∴,即:
∵O为边的中点,
∴AO2=8×9=72,
∴AO=6(负值舍去),
∴AB=12.
故选C.
7.B
解:∵在矩形中,AB=CD=9,
由折叠的性质知:AD=AF,DE=EF=9?4=5,
∵在Rt△CEF中,EF=5,CE=4,
∴CF=,
∵∠B=∠C=90°,∠AFE=90°,
∴∠BAF+∠AFB=∠AFB+∠EFC=90°,
∴∠BAF=∠EFC,
∴,
∴,即:,解得:BF=12.
故选B.
8.D
解:∵四边形ABCD是正方形,
∴∠A=∠B=90°,
∴∠AGE+∠AEG=90°,
∵∠GEF=90°,
∴∠AEG+∠BEF=90°,
∴∠AGE=∠BEF,
∴△AGE∽△BEF,
∵E为AB的中点,
∴AE=BE,
∵
解得:,
故选:B
9.C
解:∵∥,
∴∠DEF=∠A,∠DFE=∠DBA,
∴.
∵,
∴,
又∵,
∴.
∴在中,.
故选:C.
10.B
解:∵△ABC是直角三角形,∠ACB=90°,CD⊥AB于D,
∴∠1+∠2=90°,∠2+∠A=90°
∴∠1=∠A,故①正确;
∵∠A+∠B=90°,∠2+∠A=90°,
∴∠2=∠B,故②错误;
∵∠1=∠A,∠CDB=∠ADC=90°
∴△CDB∽△ADC
∴
∴CD2=AD?BD,故③正确;
∵∠1=∠A,∠CDB=∠ACB=90°
∴△CDB∽△ACB
∴
④BC2=BD?AB,故④错误;
故选C.
11.D
解:∵
∴
A.
∵
∴
∴
∴选项A正确,不符合题意;
B.∵
∴
∴
∵
∴
∴
∴
∴
故选项B正确,不符合题意;
C.∴
∴
∴
∴选项C正确,不符合题意;
D.∵,,
∴四边形AFDE是平行四边形
∴DE=AF
∵,
∴
∴
∴
故选项D错误,本选项符合题意,
故选D.
12.C
解:延长CF交BA的延长线于点G,如图所示:
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴,,
∵F是AD的中点,
∴,
∴,
∴,
∵点E是CD的中点,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∵点E是CD的中点,
∴,
∴;
故选C.
13.16:21
解:∵DE∥AC,
∴△BDE∽△BAC,且AD:DB=3:4,
∴BD:AB=DE:AC=4:7,S△BDE:S△BAC=16:49,
∴S△BDE:S四边形DECA=16:33,
∵DE:AC=4:7,△ADE与△ACE的高相等,
∴S△ADE:S△ACE=4:7=12:21,
∴S△BDE:S△AEC=16:21,
故答案为:16:21.
14.
解:如图,作,交AD于点K,
∵
∴90°,90°,,即
∴CAK
∵,
∴AKC
∴AK,CK
∵,
∴EK
∴,
∵,
∴,
∴
∵,
∴,
∴
∴
∴
∴2
故答案为:.
15.
解:∵和都是等边三角形,BD=4,CD=2,
∴AB=AC=BC=6,∠B=∠C=∠ADF=60°,
∴∠ADB+∠BAD=∠ADB+∠CDF=120°,
∴∠BAD=∠CDF,
∴,
∴,即,
解得,
∴,
故答案为:.
16.
解:∵是等腰直角三角形,,
∴△AED是等腰直角三角形,
∴AD=AE,AB=AC,
∵把绕点A逆时针旋转,
∴∠DAE=∠BAC=45°,
∴∠EAC=∠DAB,
又∵,
∴△DAB∽△EAC,
∴=,
故答案为:.
17.6
解:∵四边形ABCD中,AD//BC.
∴△AOD∽△COB.
∵AD
=
2BC.
∴AD:BC=1:2,
∴OD:OB=AD:BC=1:2,S△BOC=4
S△AOD=4
∴S△AOD:S△AOB
=1:2,即S△AOB
=2
∴S△ABC=S△BOC+
S△AOB
=4+2=6.
故填6.
18.见解析
解:过点作,交延长线于点,
∴
∴
又∵
∴
又∵
∴
∴
∴
∴
19.见解析
解:过P作于E,于F,
∵∠ACB=90°,
∴为矩形
∴,PF=EC
∴.
∴
∴
∵,
∴①,
∵在和中,于Q,
∴
又∵,
∴,
∴,
∴
∴②
由①②得
∴.
20.正方形DEFG的边长是6,面积为36.
解:设AH与DG交于点M,正方形DEFG的边长为x,
∵AH⊥BC,正方形DEFG的边EF在△ABC的边BC上,
∴
,
∵AH=10,∴
,
∵
,∴
,
∴
,
∴
,
又∵BC=15,DG=x,
∴
,解得:
,
∴正方形DEFG的面积为
.
21.OF=1
解:过点F作FD⊥AB交AB于D,则四边形ADFO为矩形
∴AO=BC=DF=4,AD=OF
∵EF是折痕
∴EF⊥AC
∴∠DEF+∠DFE=∠AEF+∠BAC=90°
∴∠BAC=∠DFE
∴△ABC∽△FDE
∴
∵AO=4,AB=8
∴
∴
又∵AE=3
∴AD=AE-DE=1
∴OF=1
22.(1)见解析;(2)1.
(1)证明∵是的角平分线
∴∠BAE=∠CAE
∵
∴∠CDA=∠CAE
∴∠BAE=∠CDA
∵∠CED=∠BEA(对顶角相等)
∴;
(2)∵,AC=CD
∴CD=2AB,即
∵
∴EC=BC-BE
∵
∴,即,解得BE=1.
相似三角形的性质
一、单选题
1.已知,且,,,,则的周长为(
)
A.
B.
C.
D.
2.如图,在中,,且,则的值为(
)
A.
B.
C.
D.
3.如图,数学兴趣小组利用硬纸板自制的Rt△ABC来测量操场旗杆MN的高度,他们通过调整测量位置,并使边AC与旗杆顶点M在同一直线上,已知AC=0.8米,BC=0.5米,目测点A到地面的距离AD=1.5米,到旗杆的水平距离AE=20米,则旗杆MN的高度为(
)
A.12米
B.12.5米
C.14米
D.15米
4.如图,在中,,则的长是(
).
A.
B.6
C.
D.
5.如图所示,在中,,,在中,,点P在上,交于点E,交于点F.当时,的值为(
).
A.1
B.2
C.3
D.4
6.如图所示,O为四边形的边的中点,,则的长是(
).
A.
B.6
C.
D.17
7.如图,将矩形沿直线折叠,顶点D恰好落在边上的F处.已知,则(
)
A.13
B.12
C.11
D.10
8.如图,在正方形中,E为的中点,G,F分别为,边上的点.若,则的长为(
).
A.2
B.5
C.
D.
9.如图,在中,,则的长为(
).
A.
B.8
C.10
D.16
10.如图,Rt△ABC中,CD⊥AB于D,下列结论中:①∠1=∠A;②∠2+∠B=90°;③CD2=AD?BD;④BC2=BD?AD,一定成立的有(
)个
A.1
B.2
C.3
D.4
11.在中,点,,分别在边,,上,与交于点,,,.则下列结论错误的是(
)
A.
B.
C.
D.
12.如图,?ABCD中,点E、F分别为边CD、AD的中点,连接BE、CF相交于点O,若△COE的面积为1,则?ABCD的面积为(
)
A.16
B.18
C.20
D.22
二、填空题
13.如图所示,D为边上一点,,交于点E,则________.
14.在中,,D是底边上一点,E是线段上一点,且,则与的数量关系为____________.
15.两个等边三角形和,点D在BC上,AC与DE交于点F,BD=4,CD=2,则AF的长为________.
16.如图1,是等腰直角三角形,,D,E分别为,上的点,且,把绕点A逆时针旋转(如图2),则的值为______.
17.如图,在四边形ABCD中,AD∥BC.BC=2AD,若S△AOD=1,则S△ABC=___.
三、解答题
18.如图,在的边和边上各取一点D和E,且使延长线与延长线相交于F,求证:
19.中,∠ACB=90°,,P是上一点,Q是上一点(不是中点),过Q且,交于M、N,求证:.
20.如图,已知正方形DEFG的边EF在△ABC的边BC上,顶点D,G分别在边AB,AC上,AH⊥BC于H.BC=15,AH=10.求正方形DEFG的边长和面积.
21.如图,矩形OABC中,AO=4,AB=8,点E,F分别在边AB,OC上,且AE=3,将矩形的部分沿直线EF翻折,点A的对应点A'恰好落在对角线AC上,求OF的长.
22.如图,是的角平分线,延长至,连结,使.
(1)求证:;
(2)若,,求的长.
参考答案
1.A
解:∵△ABC∽△A′B′C′,
∴△A′B′C′的周长
∶△ABC的周长=A′C′:AC,
∵A′C′=3cm,BC=5cm,AC=4cm,AB=7cm,
∴△A′B′C′的周长∶(5+4+7)=3:4,
∴△A′B′C′的周长为12cm,
故选:A.
2.A
解:∵
∴
∴
∴
∴
故选A
3.C
解:由题意可知:,
∴四边形为矩形
∴
又∵
∴
∴
∴
故答案为C.
4.B
解:∵如图,在Rt△ABC中,∠C=90°,CD⊥AB,
∴∠A+∠ACD=∠ACD+∠BCD=90°,
∴∠A=∠BCD,
又∵∠ADC=∠CDB=90°,
∴,
∴,
∴CD2=BD?AD=9×4=36,
∴CD=6(舍去负值).
故选:B.
5.C
解:∵在中,,,
∴AC=
,
过P作PH⊥BC于H,PQ⊥AB于Q,
则∠PQB=∠PHB=∠B=90°,
∴四边形PQBH是矩形,
∴PH=BQ,∠QPH=90°=∠MPN,PQ∥BC,
∴∠EPH+∠QPE=∠EPH+∠HPF=90°,
∴∠QPE=∠HPF,
∴△PQE∽△PHF,
∴,又PE=2PF,
∴PQ=2PH=2BQ,
∵PQ∥BC,
∴△AQP∽△ABC,
∴,
设BQ=x,则AQ=3﹣x,PQ=2x,
∴,
解得:,AP=3,
故选:C.
6.C
解:∵,∠B+∠BCO=∠AOC=∠DOC+∠AOD,
∴∠BCO=∠AOD,
又∵,
∴,
∴,即:
∵O为边的中点,
∴AO2=8×9=72,
∴AO=6(负值舍去),
∴AB=12.
故选C.
7.B
解:∵在矩形中,AB=CD=9,
由折叠的性质知:AD=AF,DE=EF=9?4=5,
∵在Rt△CEF中,EF=5,CE=4,
∴CF=,
∵∠B=∠C=90°,∠AFE=90°,
∴∠BAF+∠AFB=∠AFB+∠EFC=90°,
∴∠BAF=∠EFC,
∴,
∴,即:,解得:BF=12.
故选B.
8.D
解:∵四边形ABCD是正方形,
∴∠A=∠B=90°,
∴∠AGE+∠AEG=90°,
∵∠GEF=90°,
∴∠AEG+∠BEF=90°,
∴∠AGE=∠BEF,
∴△AGE∽△BEF,
∵E为AB的中点,
∴AE=BE,
∵
解得:,
故选:B
9.C
解:∵∥,
∴∠DEF=∠A,∠DFE=∠DBA,
∴.
∵,
∴,
又∵,
∴.
∴在中,.
故选:C.
10.B
解:∵△ABC是直角三角形,∠ACB=90°,CD⊥AB于D,
∴∠1+∠2=90°,∠2+∠A=90°
∴∠1=∠A,故①正确;
∵∠A+∠B=90°,∠2+∠A=90°,
∴∠2=∠B,故②错误;
∵∠1=∠A,∠CDB=∠ADC=90°
∴△CDB∽△ADC
∴
∴CD2=AD?BD,故③正确;
∵∠1=∠A,∠CDB=∠ACB=90°
∴△CDB∽△ACB
∴
④BC2=BD?AB,故④错误;
故选C.
11.D
解:∵
∴
A.
∵
∴
∴
∴选项A正确,不符合题意;
B.∵
∴
∴
∵
∴
∴
∴
∴
故选项B正确,不符合题意;
C.∴
∴
∴
∴选项C正确,不符合题意;
D.∵,,
∴四边形AFDE是平行四边形
∴DE=AF
∵,
∴
∴
∴
故选项D错误,本选项符合题意,
故选D.
12.C
解:延长CF交BA的延长线于点G,如图所示:
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴,,
∵F是AD的中点,
∴,
∴,
∴,
∵点E是CD的中点,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∵点E是CD的中点,
∴,
∴;
故选C.
13.16:21
解:∵DE∥AC,
∴△BDE∽△BAC,且AD:DB=3:4,
∴BD:AB=DE:AC=4:7,S△BDE:S△BAC=16:49,
∴S△BDE:S四边形DECA=16:33,
∵DE:AC=4:7,△ADE与△ACE的高相等,
∴S△ADE:S△ACE=4:7=12:21,
∴S△BDE:S△AEC=16:21,
故答案为:16:21.
14.
解:如图,作,交AD于点K,
∵
∴90°,90°,,即
∴CAK
∵,
∴AKC
∴AK,CK
∵,
∴EK
∴,
∵,
∴,
∴
∵,
∴,
∴
∴
∴
∴2
故答案为:.
15.
解:∵和都是等边三角形,BD=4,CD=2,
∴AB=AC=BC=6,∠B=∠C=∠ADF=60°,
∴∠ADB+∠BAD=∠ADB+∠CDF=120°,
∴∠BAD=∠CDF,
∴,
∴,即,
解得,
∴,
故答案为:.
16.
解:∵是等腰直角三角形,,
∴△AED是等腰直角三角形,
∴AD=AE,AB=AC,
∵把绕点A逆时针旋转,
∴∠DAE=∠BAC=45°,
∴∠EAC=∠DAB,
又∵,
∴△DAB∽△EAC,
∴=,
故答案为:.
17.6
解:∵四边形ABCD中,AD//BC.
∴△AOD∽△COB.
∵AD
=
2BC.
∴AD:BC=1:2,
∴OD:OB=AD:BC=1:2,S△BOC=4
S△AOD=4
∴S△AOD:S△AOB
=1:2,即S△AOB
=2
∴S△ABC=S△BOC+
S△AOB
=4+2=6.
故填6.
18.见解析
解:过点作,交延长线于点,
∴
∴
又∵
∴
又∵
∴
∴
∴
∴
19.见解析
解:过P作于E,于F,
∵∠ACB=90°,
∴为矩形
∴,PF=EC
∴.
∴
∴
∵,
∴①,
∵在和中,于Q,
∴
又∵,
∴,
∴,
∴
∴②
由①②得
∴.
20.正方形DEFG的边长是6,面积为36.
解:设AH与DG交于点M,正方形DEFG的边长为x,
∵AH⊥BC,正方形DEFG的边EF在△ABC的边BC上,
∴
,
∵AH=10,∴
,
∵
,∴
,
∴
,
∴
,
又∵BC=15,DG=x,
∴
,解得:
,
∴正方形DEFG的面积为
.
21.OF=1
解:过点F作FD⊥AB交AB于D,则四边形ADFO为矩形
∴AO=BC=DF=4,AD=OF
∵EF是折痕
∴EF⊥AC
∴∠DEF+∠DFE=∠AEF+∠BAC=90°
∴∠BAC=∠DFE
∴△ABC∽△FDE
∴
∵AO=4,AB=8
∴
∴
又∵AE=3
∴AD=AE-DE=1
∴OF=1
22.(1)见解析;(2)1.
(1)证明∵是的角平分线
∴∠BAE=∠CAE
∵
∴∠CDA=∠CAE
∴∠BAE=∠CDA
∵∠CED=∠BEA(对顶角相等)
∴;
(2)∵,AC=CD
∴CD=2AB,即
∵
∴EC=BC-BE
∵
∴,即,解得BE=1.
