2021-2022学年八年级数学华东师大版上册第13章全等三角形13.1_13.2同步练习题 (word版含答案)
文档属性
| 名称 | 2021-2022学年八年级数学华东师大版上册第13章全等三角形13.1_13.2同步练习题 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 127.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-31 08:38:39 | ||
图片预览




文档简介
13.1~13.2
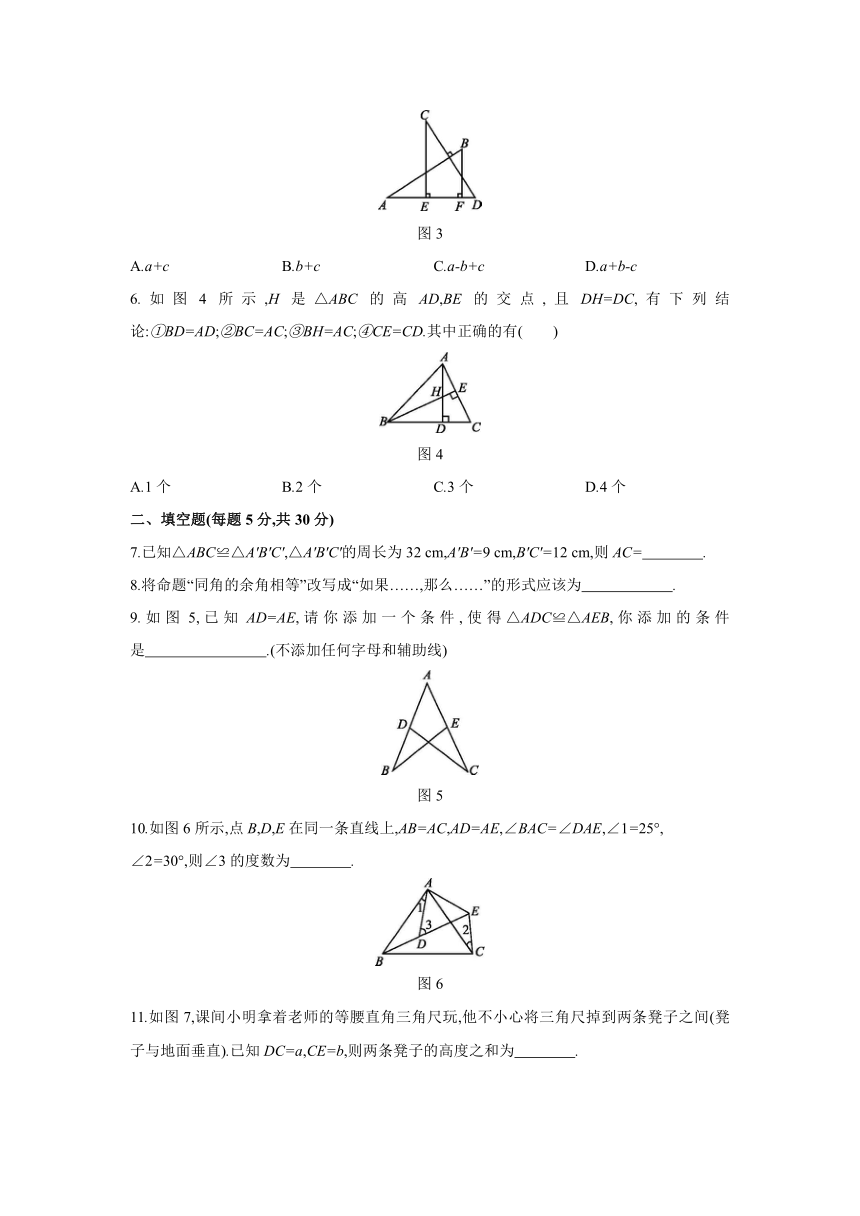
一、选择题(每题3分,共18分)
1.下列语句不是命题的是( )
A.两条直线相交,只有一个交点
B.若a=b,则a2=b2
C.不是对顶角不相等
D.作∠AOB的平分线
2.如果△ABC≌△DEF,∠A=80°,∠B=40°,那么∠F的度数是( )
A.80°
B.40°
C.60°
D.120°
3.如图1,一个三角形被纸板挡住了一部分,我们还能够画出一个与它完全重合的三角形,其原理是判定两个三角形全等的基本事实或定理,本题中用到的基本事实或定理是( )
图1
A.S.S.S.
B.S.A.S.
C.H.L.
D.A.S.A.
4.如图2,AC,BD交于点E,AC=BD,AE=BE,∠B=35°,∠1=95°,则∠D的度数是( )
图2
A.60°
B.35°
C.50°
D.75°
5.如图3,AB⊥CD,且AB=CD,E,F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为( )
图3
A.a+c
B.b+c
C.a-b+c
D.a+b-c
6.如图4所示,H是△ABC的高AD,BE的交点,且DH=DC,有下列结论:①BD=AD;②BC=AC;③BH=AC;④CE=CD.其中正确的有( )
图4
A.1个
B.2个
C.3个
D.4个
二、填空题(每题5分,共30分)
7.已知△ABC≌△A'B'C',△A'B'C'的周长为32
cm,A'B'=9
cm,B'C'=12
cm,则AC=
.?
8.将命题“同角的余角相等”改写成“如果……,那么……”的形式应该为
.?
9.如图5,已知AD=AE,请你添加一个条件,使得△ADC≌△AEB,你添加的条件是 .(不添加任何字母和辅助线)?
图5
10.如图6所示,点B,D,E在同一条直线上,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,
∠2=30°,则∠3的度数为 .?
图6
11.如图7,课间小明拿着老师的等腰直角三角尺玩,他不小心将三角尺掉到两条凳子之间(凳子与地面垂直).已知DC=a,CE=b,则两条凳子的高度之和为 .?
图7
12.在△ABC中,AB=5,AC=7,则中线AD的取值范围是 .?
三、解答题(共52分)
13.(9分)判断下列命题的真假,若是假命题,请举出一个反例.
(1)两个锐角的和是钝角;
(2)一个角的补角大于这个角;
(3)不相等的角不是对顶角.
14.(9分)如图8,已知D是AC上一点,AB=DA,DE∥AB,∠B=∠DAE.
(1)求证:BC=AE;
(2)若∠B=90°,∠C=55°,求∠EDA的度数.
图8
15.(10分)如图9,点F,B,E,C在同一直线上,并且CE=BF,∠ABC=∠DEF.能否由上面的已知条件证明△ABC≌△DEF?如果能,请给出证明;如果不能,请从下列三个条件中选择一个合适的条件,添加到已知条件中,使△ABC≌△DEF,并给出证明.
提供的三个条件:①AB=DE;②AC=DF;③AC∥DF.
图9
16.(10分)如图10,△ABC与△CDE均是等腰直角三角形,∠ACB=∠DCE=90°,点D在AB上,连结BE.请你找出一对全等三角形,并说明理由.
图10
17.(14分)如图11所示,点A,E,F,C在同一条直线上,且AE=CF,分别过点E,F作DE⊥AC,BF⊥AC,垂足分别为E,F,且AB=CD.
(1)如图①,若EF与BD相交于点G,则EG与FG相等吗?试说明理由;
(2)如果将图①中的△DEC沿AC方向移动至图②所示的位置,其余条件不变,那么(1)中的结论是否仍成立?请说明理由.
图11
答案
1.D
2.C [解析]
∵∠A=80°,∠B=40°,
∴∠C=180°-∠A-∠B=60°.
∵△ABC≌△DEF,∴∠F=∠C=60°.
故选C.
3.D [解析]
利用“A.S.A.”能判定所画三角形与原三角形全等.故选D.
4.A [解析]
∵AC=BD,AE=BE,
∴ED=EC.
在△ADE和△BCE中,
∵AE=BE,∠AED=∠BEC,ED=EC,
∴△ADE≌△BCE,
∴∠A=∠B=35°,
∴∠D=∠1-∠A=60°.
故选A.
5.D [解析]
∵AB⊥CD,CE⊥AD,BF⊥AD,
∴∠AFB=∠CED=90°,∠A+∠D=90°,∠C+∠D=90°,
∴∠A=∠C.
又∵AB=CD,∴△ABF≌△CDE,
∴AF=CE=a,BF=DE=b.
∵EF=c,
∴AD=AF+DF=a+(b-c)=a+b-c.
故选D.
6.B [解析]
∵BE⊥AC,AD⊥BC,
∴∠AEH=∠BDH=∠ADC=90°,
∴∠HBD+∠BHD=90°,∠EAH+∠AHE=90°.
又∵∠BHD=∠AHE,
∴∠HBD=∠EAH.
又∵∠BDH=∠ADC=90°,DH=DC,
∴△BDH≌△ADC(A.A.S.),
∴BD=AD,BH=AC,故①③正确.
∵BC=BD+DC,BD=AD,
∴AD+DC=BC.
在△ADC中,由三角形的三边关系知AD+DC>AC,故BC>AC,故②错误.
若CE=CD,
∵∠ACB=∠ACB,∠BEC=∠ADC=90°,
∴△BEC≌△ADC,∴BE=AD.
又∵AD=BD,∴BE=BD.
在△BDH中,易知BH>BD,即BH>BE,这与已知BH故选B.
7.11
cm [解析]
∵△A'B'C'的周长为32
cm,∴A'B'+B'C'+A'C'=32
cm,
∴A'C'=32-9-12=11(cm).∵△ABC≌△A'B'C',∴AC=A'C'=11
cm,故答案为11
cm.
8.如果两个角是同一个角的余角,那么这两个角相等
9.答案不唯一,如AB=AC或∠ADC=∠AEB或∠ABE=∠ACD [解析]
∵∠A=∠A,AD=AE,∴可以添加AB=AC,此时满足S.A.S.;添加条件∠ADC=∠AEB,此时满足A.S.A.;添加条件∠ABE=∠ACD,此时满足A.A.S..
10.55° [解析]
∵∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠1=∠EAC.
在△BAD和△CAE中,
∵AB=AC,∠1=∠EAC,AD=AE,
∴△BAD≌△CAE(S.A.S.),
∴∠ABD=∠2=30°.
∵∠1=25°,
∴∠3=∠1+∠ABD=25°+30°=55°.
故答案为55°.
11.a+b [解析]
由题意可得∠ACD+∠ECB=90°,∠ACD+∠DAC=90°,则∠DAC=∠ECB.
在△ACD和△CBE中,∵∠CDA=∠BEC=90°,∠DAC=∠ECB,AC=CB,
∴△ACD≌△CBE(A.A.S.),
故DC=EB=a,AD=CE=b,
则两条凳子的高度之和为a+b.
12.1如图,延长AD到点E,使DE=AD,连结BE.
∵AD是△ABC的中线,
∴BD=CD.
在△ADC与△EDB中,
∵CD=BD,∠ADC=∠EDB,AD=ED,
∴△ADC≌△EDB(S.A.S.),
∴AC=EB=7.
在△ABE中,根据三角形的三边关系,得
EB-AB∴2∵AE=2AD,∴113.解:(1)是假命题.例如:30°的角与40°的角的和为70°,70°的角是锐角.
(2)是假命题.例如:120°的补角为60°,60°<120°.
(3)是真命题.
14.解:(1)证明:∵DE∥AB,
∴∠CAB=∠EDA.
在△ABC和△DAE
中,
∵∠CAB=∠EDA,AB=DA,∠B=∠DAE,
∴△ABC≌△DAE(A.S.A.),∴BC=AE.
(2)∵∠B=90°,∠C=55°,
∴∠CAB=90°-∠C=90°-55°=35°.
由(1)知∠CAB=∠EDA,∴∠EDA=35°.
15.解:由题中所给的已知条件不能证明△ABC≌△DEF,需要再添加条件①或③.
若添加条件①,证明:∵CE=BF,
∴CE+BE=BF+BE,即BC=EF.
在△ABC和△DEF中,
∵AB=DE,∠ABC=∠DEF,BC=EF,
∴△ABC≌△DEF(S.A.S.).
若添加条件③,证明:∵AC∥DF,
∴∠ACB=∠DFE.
∵CE=BF,
∴CE+BE=BF+BE,即BC=EF.
在△ABC和△DEF中,
∵∠ACB=∠DFE,BC=EF,∠ABC=∠DEF,
∴△ABC≌△DEF(A.S.A.).
16.解:△ACD≌△BCE.
理由:由题意可得AC=BC,CD=CE.
∵∠ACB=∠DCE=90°,
∴∠ACB-∠DCB=∠DCE-∠DCB,
即∠ACD=∠BCE.
在△ACD和△BCE中,
∵AC=BC,∠ACD=∠BCE,CD=CE,
∴△ACD≌△BCE(S.A.S.).
17.解:(1)EG=FG.
理由:因为AE=CF,
所以AE+EF=CF+EF,即AF=CE.
因为BF⊥AC,DE⊥AC,
所以∠AFB=∠CED=90°.
在Rt△ABF和Rt△CDE中,
因为AF=CE,AB=CD,
所以Rt△ABF≌Rt△CDE(H.L.),
所以BF=DE.
在△DEG和△BFG中,因为∠DEG=∠BFG=90°,∠DGE=∠BGF,DE=BF,
所以△DEG≌△BFG(A.A.S.),
所以EG=FG.
(2)成立,仍有EG=FG.
理由:因为AE=CF,
所以AE-EF=CF-EF,即AF=CE.
因为BF⊥AC,DE⊥AC,
所以∠AFB=∠CED=90°.
在Rt△ABF和Rt△CDE中,
因为AF=CE,AB=CD,
所以Rt△ABF≌Rt△CDE(H.L.),
所以BF=DE.
在△DEG和△BFG中,因为∠DEG=∠BFG=90°,∠DGE=∠BGF,DE=BF,
所以△DEG≌△BFG(A.A.S.),
所以EG=FG.
一、选择题(每题3分,共18分)
1.下列语句不是命题的是( )
A.两条直线相交,只有一个交点
B.若a=b,则a2=b2
C.不是对顶角不相等
D.作∠AOB的平分线
2.如果△ABC≌△DEF,∠A=80°,∠B=40°,那么∠F的度数是( )
A.80°
B.40°
C.60°
D.120°
3.如图1,一个三角形被纸板挡住了一部分,我们还能够画出一个与它完全重合的三角形,其原理是判定两个三角形全等的基本事实或定理,本题中用到的基本事实或定理是( )
图1
A.S.S.S.
B.S.A.S.
C.H.L.
D.A.S.A.
4.如图2,AC,BD交于点E,AC=BD,AE=BE,∠B=35°,∠1=95°,则∠D的度数是( )
图2
A.60°
B.35°
C.50°
D.75°
5.如图3,AB⊥CD,且AB=CD,E,F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为( )
图3
A.a+c
B.b+c
C.a-b+c
D.a+b-c
6.如图4所示,H是△ABC的高AD,BE的交点,且DH=DC,有下列结论:①BD=AD;②BC=AC;③BH=AC;④CE=CD.其中正确的有( )
图4
A.1个
B.2个
C.3个
D.4个
二、填空题(每题5分,共30分)
7.已知△ABC≌△A'B'C',△A'B'C'的周长为32
cm,A'B'=9
cm,B'C'=12
cm,则AC=
.?
8.将命题“同角的余角相等”改写成“如果……,那么……”的形式应该为
.?
9.如图5,已知AD=AE,请你添加一个条件,使得△ADC≌△AEB,你添加的条件是 .(不添加任何字母和辅助线)?
图5
10.如图6所示,点B,D,E在同一条直线上,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,
∠2=30°,则∠3的度数为 .?
图6
11.如图7,课间小明拿着老师的等腰直角三角尺玩,他不小心将三角尺掉到两条凳子之间(凳子与地面垂直).已知DC=a,CE=b,则两条凳子的高度之和为 .?
图7
12.在△ABC中,AB=5,AC=7,则中线AD的取值范围是 .?
三、解答题(共52分)
13.(9分)判断下列命题的真假,若是假命题,请举出一个反例.
(1)两个锐角的和是钝角;
(2)一个角的补角大于这个角;
(3)不相等的角不是对顶角.
14.(9分)如图8,已知D是AC上一点,AB=DA,DE∥AB,∠B=∠DAE.
(1)求证:BC=AE;
(2)若∠B=90°,∠C=55°,求∠EDA的度数.
图8
15.(10分)如图9,点F,B,E,C在同一直线上,并且CE=BF,∠ABC=∠DEF.能否由上面的已知条件证明△ABC≌△DEF?如果能,请给出证明;如果不能,请从下列三个条件中选择一个合适的条件,添加到已知条件中,使△ABC≌△DEF,并给出证明.
提供的三个条件:①AB=DE;②AC=DF;③AC∥DF.
图9
16.(10分)如图10,△ABC与△CDE均是等腰直角三角形,∠ACB=∠DCE=90°,点D在AB上,连结BE.请你找出一对全等三角形,并说明理由.
图10
17.(14分)如图11所示,点A,E,F,C在同一条直线上,且AE=CF,分别过点E,F作DE⊥AC,BF⊥AC,垂足分别为E,F,且AB=CD.
(1)如图①,若EF与BD相交于点G,则EG与FG相等吗?试说明理由;
(2)如果将图①中的△DEC沿AC方向移动至图②所示的位置,其余条件不变,那么(1)中的结论是否仍成立?请说明理由.
图11
答案
1.D
2.C [解析]
∵∠A=80°,∠B=40°,
∴∠C=180°-∠A-∠B=60°.
∵△ABC≌△DEF,∴∠F=∠C=60°.
故选C.
3.D [解析]
利用“A.S.A.”能判定所画三角形与原三角形全等.故选D.
4.A [解析]
∵AC=BD,AE=BE,
∴ED=EC.
在△ADE和△BCE中,
∵AE=BE,∠AED=∠BEC,ED=EC,
∴△ADE≌△BCE,
∴∠A=∠B=35°,
∴∠D=∠1-∠A=60°.
故选A.
5.D [解析]
∵AB⊥CD,CE⊥AD,BF⊥AD,
∴∠AFB=∠CED=90°,∠A+∠D=90°,∠C+∠D=90°,
∴∠A=∠C.
又∵AB=CD,∴△ABF≌△CDE,
∴AF=CE=a,BF=DE=b.
∵EF=c,
∴AD=AF+DF=a+(b-c)=a+b-c.
故选D.
6.B [解析]
∵BE⊥AC,AD⊥BC,
∴∠AEH=∠BDH=∠ADC=90°,
∴∠HBD+∠BHD=90°,∠EAH+∠AHE=90°.
又∵∠BHD=∠AHE,
∴∠HBD=∠EAH.
又∵∠BDH=∠ADC=90°,DH=DC,
∴△BDH≌△ADC(A.A.S.),
∴BD=AD,BH=AC,故①③正确.
∵BC=BD+DC,BD=AD,
∴AD+DC=BC.
在△ADC中,由三角形的三边关系知AD+DC>AC,故BC>AC,故②错误.
若CE=CD,
∵∠ACB=∠ACB,∠BEC=∠ADC=90°,
∴△BEC≌△ADC,∴BE=AD.
又∵AD=BD,∴BE=BD.
在△BDH中,易知BH>BD,即BH>BE,这与已知BH
7.11
cm [解析]
∵△A'B'C'的周长为32
cm,∴A'B'+B'C'+A'C'=32
cm,
∴A'C'=32-9-12=11(cm).∵△ABC≌△A'B'C',∴AC=A'C'=11
cm,故答案为11
cm.
8.如果两个角是同一个角的余角,那么这两个角相等
9.答案不唯一,如AB=AC或∠ADC=∠AEB或∠ABE=∠ACD [解析]
∵∠A=∠A,AD=AE,∴可以添加AB=AC,此时满足S.A.S.;添加条件∠ADC=∠AEB,此时满足A.S.A.;添加条件∠ABE=∠ACD,此时满足A.A.S..
10.55° [解析]
∵∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠1=∠EAC.
在△BAD和△CAE中,
∵AB=AC,∠1=∠EAC,AD=AE,
∴△BAD≌△CAE(S.A.S.),
∴∠ABD=∠2=30°.
∵∠1=25°,
∴∠3=∠1+∠ABD=25°+30°=55°.
故答案为55°.
11.a+b [解析]
由题意可得∠ACD+∠ECB=90°,∠ACD+∠DAC=90°,则∠DAC=∠ECB.
在△ACD和△CBE中,∵∠CDA=∠BEC=90°,∠DAC=∠ECB,AC=CB,
∴△ACD≌△CBE(A.A.S.),
故DC=EB=a,AD=CE=b,
则两条凳子的高度之和为a+b.
12.1
∵AD是△ABC的中线,
∴BD=CD.
在△ADC与△EDB中,
∵CD=BD,∠ADC=∠EDB,AD=ED,
∴△ADC≌△EDB(S.A.S.),
∴AC=EB=7.
在△ABE中,根据三角形的三边关系,得
EB-AB
(2)是假命题.例如:120°的补角为60°,60°<120°.
(3)是真命题.
14.解:(1)证明:∵DE∥AB,
∴∠CAB=∠EDA.
在△ABC和△DAE
中,
∵∠CAB=∠EDA,AB=DA,∠B=∠DAE,
∴△ABC≌△DAE(A.S.A.),∴BC=AE.
(2)∵∠B=90°,∠C=55°,
∴∠CAB=90°-∠C=90°-55°=35°.
由(1)知∠CAB=∠EDA,∴∠EDA=35°.
15.解:由题中所给的已知条件不能证明△ABC≌△DEF,需要再添加条件①或③.
若添加条件①,证明:∵CE=BF,
∴CE+BE=BF+BE,即BC=EF.
在△ABC和△DEF中,
∵AB=DE,∠ABC=∠DEF,BC=EF,
∴△ABC≌△DEF(S.A.S.).
若添加条件③,证明:∵AC∥DF,
∴∠ACB=∠DFE.
∵CE=BF,
∴CE+BE=BF+BE,即BC=EF.
在△ABC和△DEF中,
∵∠ACB=∠DFE,BC=EF,∠ABC=∠DEF,
∴△ABC≌△DEF(A.S.A.).
16.解:△ACD≌△BCE.
理由:由题意可得AC=BC,CD=CE.
∵∠ACB=∠DCE=90°,
∴∠ACB-∠DCB=∠DCE-∠DCB,
即∠ACD=∠BCE.
在△ACD和△BCE中,
∵AC=BC,∠ACD=∠BCE,CD=CE,
∴△ACD≌△BCE(S.A.S.).
17.解:(1)EG=FG.
理由:因为AE=CF,
所以AE+EF=CF+EF,即AF=CE.
因为BF⊥AC,DE⊥AC,
所以∠AFB=∠CED=90°.
在Rt△ABF和Rt△CDE中,
因为AF=CE,AB=CD,
所以Rt△ABF≌Rt△CDE(H.L.),
所以BF=DE.
在△DEG和△BFG中,因为∠DEG=∠BFG=90°,∠DGE=∠BGF,DE=BF,
所以△DEG≌△BFG(A.A.S.),
所以EG=FG.
(2)成立,仍有EG=FG.
理由:因为AE=CF,
所以AE-EF=CF-EF,即AF=CE.
因为BF⊥AC,DE⊥AC,
所以∠AFB=∠CED=90°.
在Rt△ABF和Rt△CDE中,
因为AF=CE,AB=CD,
所以Rt△ABF≌Rt△CDE(H.L.),
所以BF=DE.
在△DEG和△BFG中,因为∠DEG=∠BFG=90°,∠DGE=∠BGF,DE=BF,
所以△DEG≌△BFG(A.A.S.),
所以EG=FG.
