2021-2022学年八年级数学华东师大版上册第十二章12.3乘法公式同步练习卷(word版含答案)
文档属性
| 名称 | 2021-2022学年八年级数学华东师大版上册第十二章12.3乘法公式同步练习卷(word版含答案) | 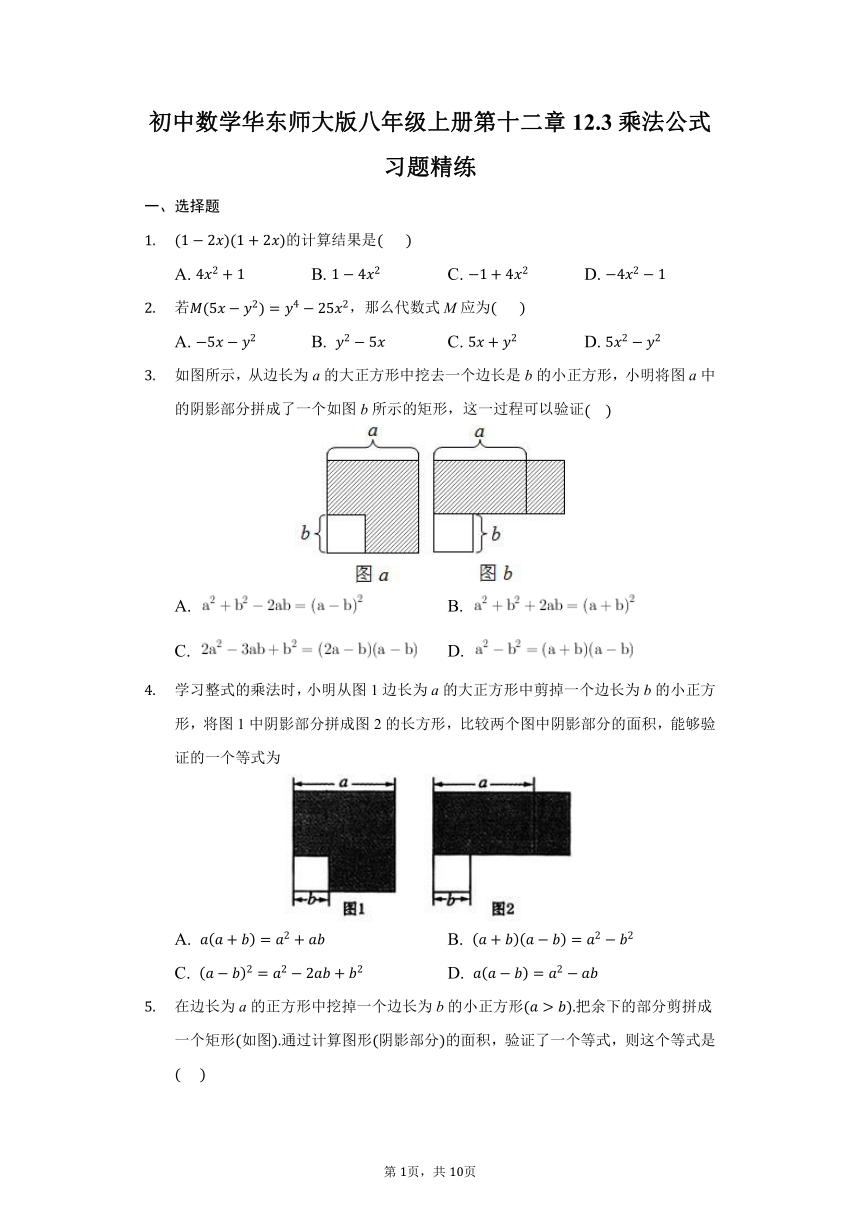 | |
| 格式 | docx | ||
| 文件大小 | 243.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-31 08:42:10 | ||
图片预览



文档简介
初中数学华东师大版八年级上册第十二章12.3乘法公式习题精练
一、选择题
的计算结果是?
?
A.
B.
C.
D.
若,那么代数式M应为?
?
A.
B.
C.
D.
如图所示,从边长为a的大正方形中挖去一个边长是b的小正方形,小明将图a中的阴影部分拼成了一个如图b所示的矩形,这一过程可以验证
A.
B.
C.
D.
学习整式的乘法时,小明从图1边长为a的大正方形中剪掉一个边长为b的小正方形,将图1中阴影部分拼成图2的长方形,比较两个图中阴影部分的面积,能够验证的一个等式为
A.
B.
C.
D.
在边长为a的正方形中挖掉一个边长为b的小正方形把余下的部分剪拼成一个矩形如图通过计算图形阴影部分的面积,验证了一个等式,则这个等式是???
A.
B.
C.
D.
计算的结果是?
?
A.
12xy
B.
C.
6xy
D.
下列运算正确的是?
?
A.
B.
C.
D.
若是完全平方式,则k值是???
A.
B.
C.
D.
1
代数式是一个完全平方式,则k的值为
A.
7
B.
C.
14
D.
4张长为a、宽为的长方形纸片按如图所示的方式拼成一个边长为的正方形,图中空白部分的面积为,阴影部分的面积为若,则a、b满足?
?
A.
B.
C.
D.
二、填空题
如图,边长为的正方形纸片剪出一个边长为的正方形之后,剩余部分可剪拼成一个长方形,若拼成的长方形一边长为m,则这个长方形的周长为______.
如图1,将边长为a的大正方形剪去一个边长为b的小正方形,再沿图中的虚线剪开,然后按图2所示进行拼接,请根据图形的面积写出一个含字母a,b的等式______.
已知且,则??????????.
根据题意列出代数式:
在一个大正方形铁片中挖去一个小正方形铁片,大正方形的边长是a厘米,小正方形的边长是b厘米,剩余部分的面积是______
.
若是一个完全平方式,则??????????.
如果二次三项式能配成完全平方式,那么m的值是_________
三、解答题
如图1,从边长为a的正方形纸片中剪去一个边长为b的小正方形,再沿着虚线剪开,把剪成的两张纸片拼成如图2所示的长方形.
设图1中的阴影部分面积为,图2中的阴影部分面积为,请直接用含有a、b的代数式表示,则________,_______________;
请写出上述剪拼过程所揭示的乘法公式:_______________________;
请你利用中的公式计算:.
从边长为a的正方形中剪掉一个边长为b的正方形如图,然后将剩余部分拼成一个长方形如图.
上述操作能验证的等式是____;请选择正确的一个
A、???B、???
C、
应用你从选出的等式,完成下列各题:
已知,,求的值.
计算:
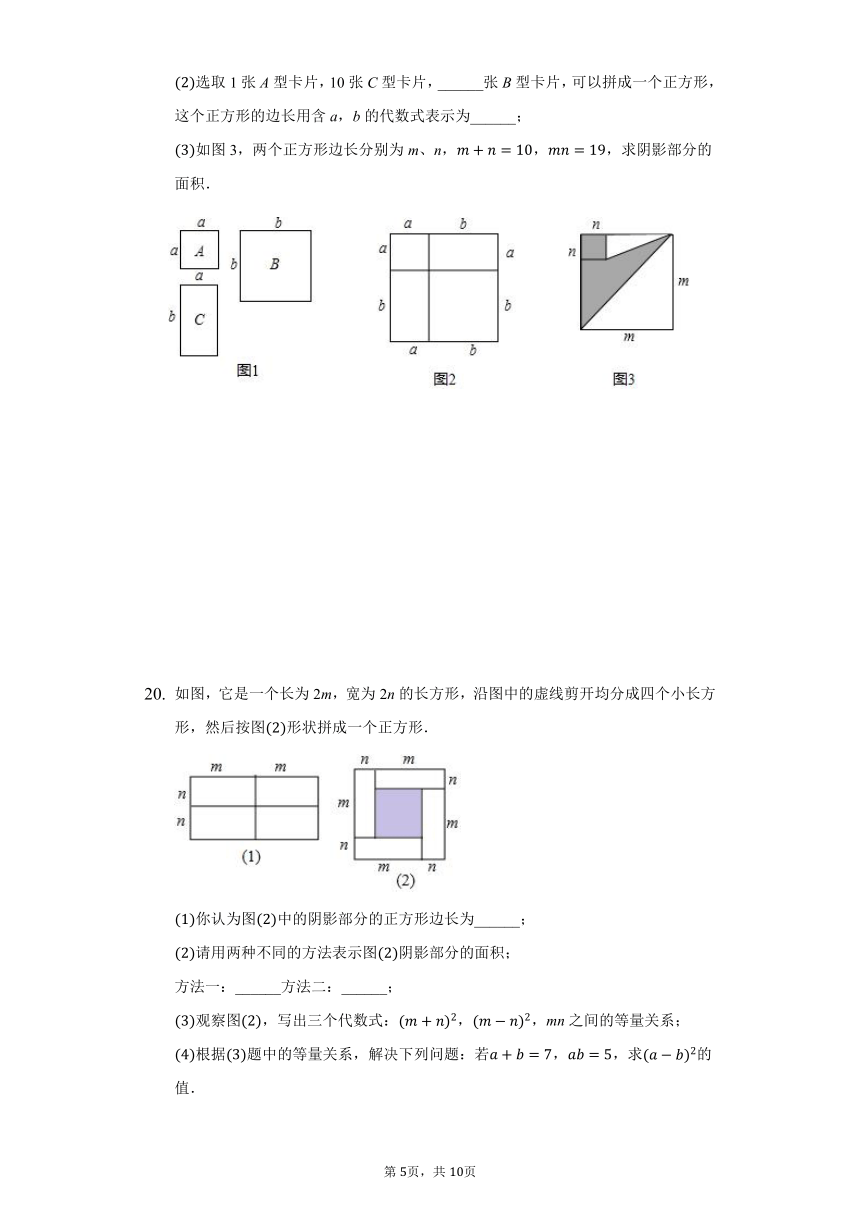
如图1,有A型、B型正方形卡片和C型长方形卡片各若干张.
用1张A型卡片,1张B型卡片,2张C型卡片拼成一个正方形,如图2,用两种方法计算这个正方形面积,可以得到一个等式,请你写出这个等式;
选取1张A型卡片,10张C型卡片,______张B型卡片,可以拼成一个正方形,这个正方形的边长用含a,b的代数式表示为______;
如图3,两个正方形边长分别为m、n,,,求阴影部分的面积.
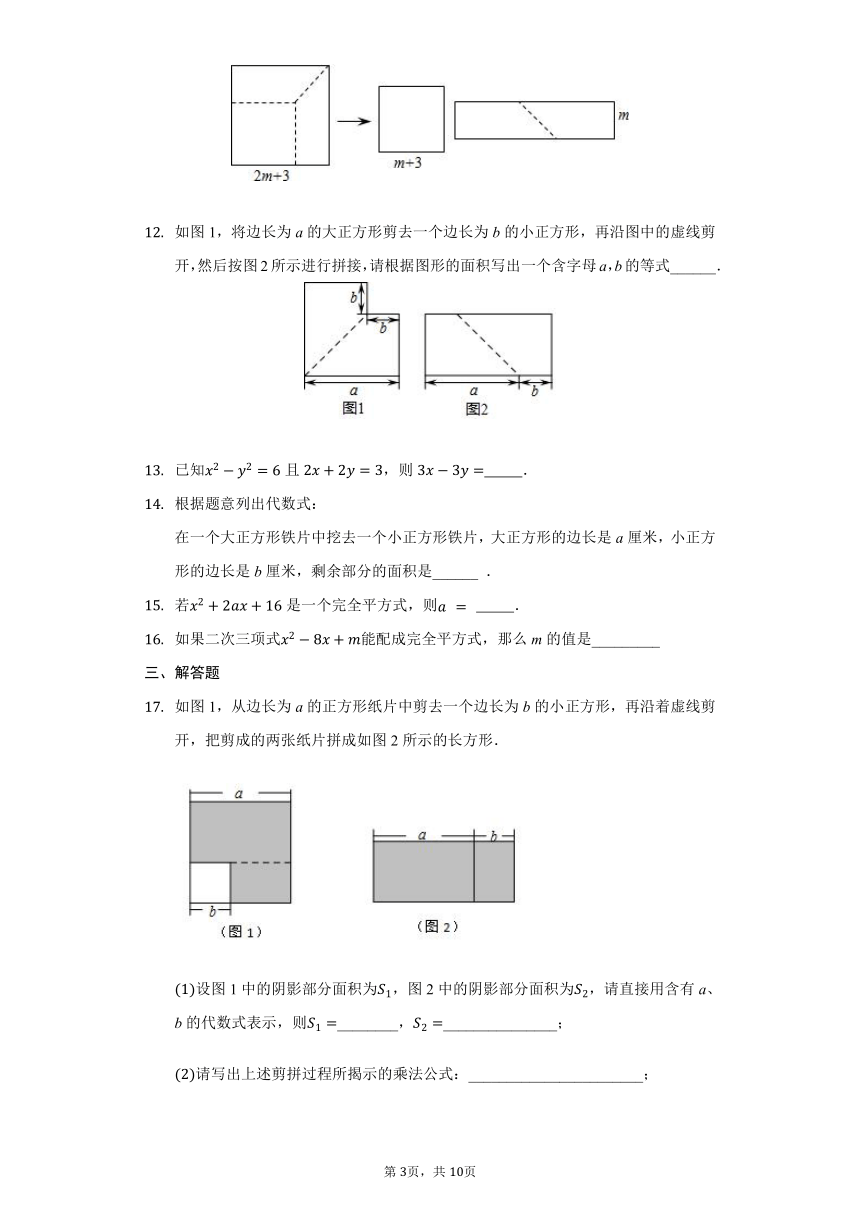
如图,它是一个长为2m,宽为2n的长方形,沿图中的虚线剪开均分成四个小长方形,然后按图形状拼成一个正方形.
你认为图中的阴影部分的正方形边长为______;
请用两种不同的方法表示图阴影部分的面积;
方法一:______方法二:______;
观察图,写出三个代数式:,,mn之间的等量关系;
根据题中的等量关系,解决下列问题:若,,求的值.
答案和解析
【答案】B
【解析】,故选B.
2.【答案】A
【解析】?,
.
故选A.
3.【答案】D
【解析】解:由题可知.
故选D.??
4.【答案】B
【解析】解:图1中阴影部分的面积,图2中阴影部分的面积,
而两个图形中阴影部分的面积相等,
.故选B.??
5.【答案】A
【解析】解:由图可知,大正方形减小正方形剩下的部分面积为;
拼成的长方形的面积:,
所以得出:,故选:A.??
6.【答案】A
【解析】原式
.
故选A.
7.【答案】D
【解析】A.,故本选项不合题意
B.,故本选项不合题意
C.,故本选项不合题意
D.,故本选项符合题意.
故选D.
8.【答案】B
【解析】解:是一个完全平方公式,
,故选B.??
9.【答案】D
【解析】
解:是一个完全平方式,
,
解得.故选:D.??
10.【答案】D
【解析】由题图可知
,
,
,
?,整理得,
,
.
故选D.
11.【答案】
【解析】解:,拼成的长方形一边长为m,
长方形的长为:.
这个长方形的周长为:.
故答案为:.
12.【答案】
【解析】解:图1面积为,图2的面积为,
因此有:,
故答案为:.
13.【答案】12
【解析】解:由可得,
,
,
.
14.【答案】
【解析】解:大正方形的面积为,小正方形的面积为,所以剩余部分的面积为.
故答案为:.
15.【答案】
【解析】解:,
,故答案为.??
16.【答案】16
【解析】解:二次三项式是一个完全平方式,
,
.故答案为16.
??17.【答案】解:;?;
;
原式
【解析】解:由题意得
,.
故答案为;?;
由得,.
,
故答案为?;
见答案.??
18.【答案】解:;
,
得:;
原式
.
19.【答案】25?
【解析】解:方法1:大正方形的面积为,
方法2:图2中四部分的面积和为:,
因此有,
由面积拼图可知,
故答案为:25,,
由图形面积之间的关系可得,
.
用两种方法表示图2的面积,即可得出等式;
由拼图可得是完全平方式,则,即,从而得出答案;
表示阴影部分的面积,化成,再整体代入求值即可.
考查完全平方公式的几何意义,用不同方法表示同一个图形的面积是常用的方法.
20.【答案】;
?
,;
关系为:;
;
有
又,
.
第2页,共3页
第1页,共1页
一、选择题
的计算结果是?
?
A.
B.
C.
D.
若,那么代数式M应为?
?
A.
B.
C.
D.
如图所示,从边长为a的大正方形中挖去一个边长是b的小正方形,小明将图a中的阴影部分拼成了一个如图b所示的矩形,这一过程可以验证
A.
B.
C.
D.
学习整式的乘法时,小明从图1边长为a的大正方形中剪掉一个边长为b的小正方形,将图1中阴影部分拼成图2的长方形,比较两个图中阴影部分的面积,能够验证的一个等式为
A.
B.
C.
D.
在边长为a的正方形中挖掉一个边长为b的小正方形把余下的部分剪拼成一个矩形如图通过计算图形阴影部分的面积,验证了一个等式,则这个等式是???
A.
B.
C.
D.
计算的结果是?
?
A.
12xy
B.
C.
6xy
D.
下列运算正确的是?
?
A.
B.
C.
D.
若是完全平方式,则k值是???
A.
B.
C.
D.
1
代数式是一个完全平方式,则k的值为
A.
7
B.
C.
14
D.
4张长为a、宽为的长方形纸片按如图所示的方式拼成一个边长为的正方形,图中空白部分的面积为,阴影部分的面积为若,则a、b满足?
?
A.
B.
C.
D.
二、填空题
如图,边长为的正方形纸片剪出一个边长为的正方形之后,剩余部分可剪拼成一个长方形,若拼成的长方形一边长为m,则这个长方形的周长为______.
如图1,将边长为a的大正方形剪去一个边长为b的小正方形,再沿图中的虚线剪开,然后按图2所示进行拼接,请根据图形的面积写出一个含字母a,b的等式______.
已知且,则??????????.
根据题意列出代数式:
在一个大正方形铁片中挖去一个小正方形铁片,大正方形的边长是a厘米,小正方形的边长是b厘米,剩余部分的面积是______
.
若是一个完全平方式,则??????????.
如果二次三项式能配成完全平方式,那么m的值是_________
三、解答题
如图1,从边长为a的正方形纸片中剪去一个边长为b的小正方形,再沿着虚线剪开,把剪成的两张纸片拼成如图2所示的长方形.
设图1中的阴影部分面积为,图2中的阴影部分面积为,请直接用含有a、b的代数式表示,则________,_______________;
请写出上述剪拼过程所揭示的乘法公式:_______________________;
请你利用中的公式计算:.
从边长为a的正方形中剪掉一个边长为b的正方形如图,然后将剩余部分拼成一个长方形如图.
上述操作能验证的等式是____;请选择正确的一个
A、???B、???
C、
应用你从选出的等式,完成下列各题:
已知,,求的值.
计算:
如图1,有A型、B型正方形卡片和C型长方形卡片各若干张.
用1张A型卡片,1张B型卡片,2张C型卡片拼成一个正方形,如图2,用两种方法计算这个正方形面积,可以得到一个等式,请你写出这个等式;
选取1张A型卡片,10张C型卡片,______张B型卡片,可以拼成一个正方形,这个正方形的边长用含a,b的代数式表示为______;
如图3,两个正方形边长分别为m、n,,,求阴影部分的面积.
如图,它是一个长为2m,宽为2n的长方形,沿图中的虚线剪开均分成四个小长方形,然后按图形状拼成一个正方形.
你认为图中的阴影部分的正方形边长为______;
请用两种不同的方法表示图阴影部分的面积;
方法一:______方法二:______;
观察图,写出三个代数式:,,mn之间的等量关系;
根据题中的等量关系,解决下列问题:若,,求的值.
答案和解析
【答案】B
【解析】,故选B.
2.【答案】A
【解析】?,
.
故选A.
3.【答案】D
【解析】解:由题可知.
故选D.??
4.【答案】B
【解析】解:图1中阴影部分的面积,图2中阴影部分的面积,
而两个图形中阴影部分的面积相等,
.故选B.??
5.【答案】A
【解析】解:由图可知,大正方形减小正方形剩下的部分面积为;
拼成的长方形的面积:,
所以得出:,故选:A.??
6.【答案】A
【解析】原式
.
故选A.
7.【答案】D
【解析】A.,故本选项不合题意
B.,故本选项不合题意
C.,故本选项不合题意
D.,故本选项符合题意.
故选D.
8.【答案】B
【解析】解:是一个完全平方公式,
,故选B.??
9.【答案】D
【解析】
解:是一个完全平方式,
,
解得.故选:D.??
10.【答案】D
【解析】由题图可知
,
,
,
?,整理得,
,
.
故选D.
11.【答案】
【解析】解:,拼成的长方形一边长为m,
长方形的长为:.
这个长方形的周长为:.
故答案为:.
12.【答案】
【解析】解:图1面积为,图2的面积为,
因此有:,
故答案为:.
13.【答案】12
【解析】解:由可得,
,
,
.
14.【答案】
【解析】解:大正方形的面积为,小正方形的面积为,所以剩余部分的面积为.
故答案为:.
15.【答案】
【解析】解:,
,故答案为.??
16.【答案】16
【解析】解:二次三项式是一个完全平方式,
,
.故答案为16.
??17.【答案】解:;?;
;
原式
【解析】解:由题意得
,.
故答案为;?;
由得,.
,
故答案为?;
见答案.??
18.【答案】解:;
,
得:;
原式
.
19.【答案】25?
【解析】解:方法1:大正方形的面积为,
方法2:图2中四部分的面积和为:,
因此有,
由面积拼图可知,
故答案为:25,,
由图形面积之间的关系可得,
.
用两种方法表示图2的面积,即可得出等式;
由拼图可得是完全平方式,则,即,从而得出答案;
表示阴影部分的面积,化成,再整体代入求值即可.
考查完全平方公式的几何意义,用不同方法表示同一个图形的面积是常用的方法.
20.【答案】;
?
,;
关系为:;
;
有
又,
.
第2页,共3页
第1页,共1页
