苏教版六年级上册数学第一单元综合提优测评卷(word版,含答案)
文档属性
| 名称 | 苏教版六年级上册数学第一单元综合提优测评卷(word版,含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-29 00:00:00 | ||
图片预览



文档简介
第一单元综合提优测评卷(B)
(时间:60分钟总分:100分)
一、填一填。(每空1分,共26分)
1.(1)一个梨的体积约是115( )。
(2)一只铝锅能盛5( )水。
(3)一个仓库的容积约是220( )。
(4)
一个茶杯可以装水500( )。
2.
250立方分米
=
( )立方米
0.8升
=
( )立方厘米
2立方米30立方分米
=
( )立方米
3.(2020·无锡惠山区期末)一个长方体工艺盒(如右图),框架由铝合金条制成,各个面都用灯箱布围成。制成这个工艺盒,至少需要铝合金条( )厘米;需要灯箱布( )平方厘米(接头处不计);如果工艺盒里面放一些棱长3厘米的正方体木块,最多能放( )块。
4.(2020·福建宁随市期末)一个棱长为1分米的正方体,切割成棱长为1厘米的小正方体,把这些小正方体摆成一行长为( )米。
5.至少需要( )厘米长的铁丝,才能做一个底面周长是18厘米,高是3厘米的长方体框架。
6.把一个棱长是4厘米的正方体切成两个长方体,它的表面积增加了( )平方厘米。
7.把一个长方体切成三个一样的正方体,表面积增加40平方厘米,原来长方体的表面积是
( )平方厘米。
8.一张长方形纸的长是40厘米、宽是8厘米。把它对折、再对折。打开后,就能围成一个高是8厘米的长方体的侧面。如果要为这个长方体配一个底面,那么这个底面的面积是( )平方厘米,围成长方体的体积是( )立方厘米。
9.左下图是一个长方体纸盒的展开图(单位:dm),这个纸盒的用料面积是( )dm2。
10.将2升水倒入右上图中的两个长方体水槽中,使它们的水面高度相等,这个高度是( )厘米。(单位:厘米)
11.在一个长9分米、宽8分米、高7分米的长方体木盒内,最多可以放入( )个棱长为2分米的小正方体木块。
12.(2020·淮安淮安区期末)右图所示的长方体体积是( )立方
厘米,如果沿虚线切开,那么表面积比原来增加( )平方厘米。
13.若把一块不规则的铁块全部浸入底面积为180平方厘米的长方体鱼缸中,水面上升了3厘米且水未溢出,则这块铁块的体积是( )立方厘米。
14.一个棱长1米的正方体水池,蓄水的水面低于池口2分米,池内蓄水( )升。
15.(2020·南京江宁区期末)(1)右图中,小正方体的棱长为1厘米,这个立体图形的体积是( )立方厘米;表面积是( )平方厘米。
(2)至少移动其中( )个小正方体可以将这个立体图形变成一个体积不变的长方体。
二、选一选。(每题1分,共8分)
1.(2020·淮安淮安区期末)下面不能沿虚线折成正方体的是( )。
2.一个长方体的棱长之和是52厘米,相交于一个顶点的所有棱长之和是( )。
A.13厘米
B.15厘米
C.14厘米
D.16厘米
3.(2020·无锡惠山区期末)一个长9厘米、宽6厘米、高3厘米的长方体,切割成3个体积相等的长方体,表面积最多可增加( )平方厘米。
A.216
B.108
C.72
D.36
(2020·淮安淮安区期末)小红用一些1
dm3的
小正方体摆成一个长方体,从正面、左面和上面
看到的图形分别如右图所示,这个长方体的体积是( )dm3。
A.52
B.24
C.18
5.将一块长为5分米、宽为6分米、高为0.3米的长方体木料,锯成棱长是1分米的小正方体,可以锯成( )。
A.9块
B.90块
C.18块
D.180块
6.把一块体积为20立方厘米的铁块沉入一个底面长为5厘米、宽为2厘米的长方体玻璃容器中,水面会上升( )。(铁块完全浸没在水中且水未溢出)
A.20厘米
B.2厘米
C.4厘米
D.无法确定
7.一个长方体的盒子,从里面量,长8分米、宽5分米、高4分米。如果把棱长为2分米的正方体木块放到这个盒子里,那么最多能放( )。
A.12个
B.14个
C.20个
D.16个
8.将一个长为6厘米、宽为5厘米、高为4厘米的长方体截成一个体积最大的正方体,这个正方体的体积是( )。
A.125立方厘米
B.125平方厘米
C.64立方厘米
D.64平方厘米
三、判一判。(每题1分,共5分)
1.一个正方体的体积是1立方厘米,它的底面周长是4厘米。
(
)
2.表面积相等的两个正方体,它们的体积也相等。
(
)
3.把两个完全一样的正方体拼成一个长方体,体积和表面积都不变。
(
)
4.至少4个完全一样的小正方体才能拼成一个较大的正方体。
(
)
5.如果甲容器的体积比乙容器的体积大,那么甲容器的容积一定比乙容器的容积大。(
)
四、计算题。(第3题5分,其余每题8分,共21分)
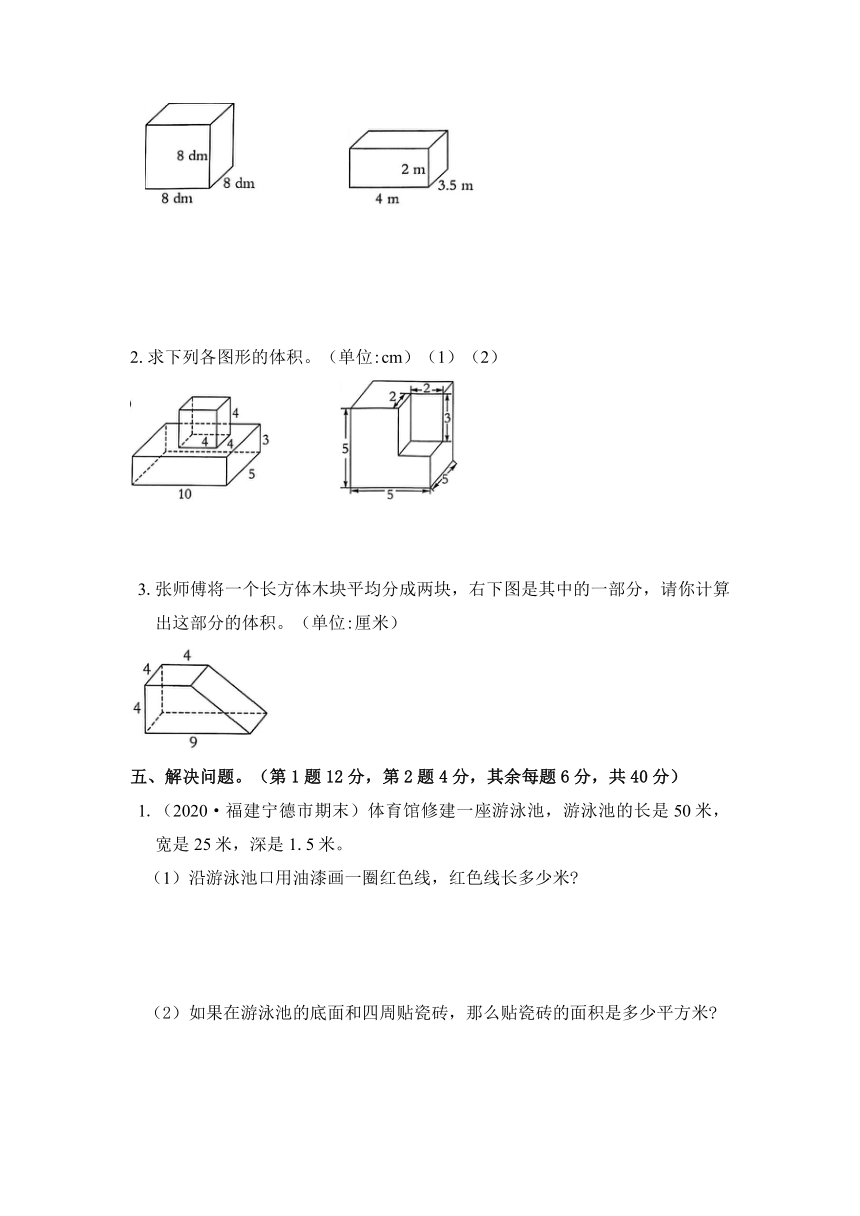
1.求下列各图形的表面积和体积。
2.求下列各图形的体积。(单位:cm)(1)(2)
3.张师傅将一个长方体木块平均分成两块,右下图是其中的一部分,请你计算出这部分的体积。(单位:厘米)
五、解决问题。(第1题12分,第2题4分,其余每题6分,共40分)
1.(2020·福建宁德市期末)体育馆修建一座游泳池,游泳池的长是50米,宽是25米,深是1.5米。
(1)沿游泳池口用油漆画一圈红色线,红色线长多少米?
如果在游泳池的底面和四周贴瓷砖,那么贴瓷砖的面积是多少平方米?
(3)如果往游泳池里放水,使水面到池口的距离是0.2米,那么需要多少立方米水?
2.粮店售米用的木箱(无盖)长为1.2米,宽为0.5米,高为0.8米。做这样一个木箱至少需要多少平方米的木料?
3.用50本数学课本摆成一个长是18厘米、宽是13厘米、高是25厘米的长方体,平均每本书的体积是多少立方厘米?
4.一个长方体容器,长为4分米,宽为2.5分米,高为3分米,一个铁块完全浸入水中后(水未溢出),水面升高了1.2分米。这个铁块的体积是多少?
5.一个长方体的棱长总和是440厘米,已知长是宽的2倍,宽是高的1.5倍。这个长方体的长、宽、高分别是多少厘米?
6.一个封闭的长方体容器,长、宽、高分别是10厘米、10厘米和15厘米。长方体容器里面装着水,张明不小心把容器碰倒了。
精挑好题。
(2020·南通如东县期末)右图是用棱长为1厘米的小正方体拼成的大长方体。
(1)拼成这个图形用了( )个小正方体,拼成图形的表面积是(
)平方厘米。
(2)给拼成图形的表面涂色后,再全都分开,其中两面涂色的有( )块,一面涂色的有( )块。
第一单元综合提优测评卷(B)
1.(1)立方厘米
(2)升
(3)立方米
(4)毫升
2.
0.25
800
2.03
[提示]把高级单位的名数改写成低级单位的名数,用高级单位前面的数乘进率。把低级单位的名数改写成高级单位的名数,用低级单位前面的数除以进率。
3.
220
1800
150
[提示]长方体中有4条长、4条宽、4条高,求至少需要铝条多少厘米,就是求棱长总和,列式是(15
+
10
+
30)×
4
=
220(厘米)。
4.
10
5.48
6.
32
[提示]把一个棱长是4厘米的正方体切成两个长方体,表面积增加了2个与原正方形右面相等的正方形,所以它的表面积增加了4
×
4
×
2
=
32(平方厘米)。
7.
140
8.
100
800
9.
88
10.
12.5
11.
48
[提示]把棱长为2分米的小正方体木块放入长方体木盒内,密放后组成的长方体的长、宽、高都是2的倍数,9
÷
2
=
4(个)…1(分米),8
÷
2
=
4(个),7
÷
2
=
3(个)…1(分米),放的个数为4
×
4
×
3
=
48(个)。
12.
120
88
[提示]看图可以发现表面积比原来增加的面积等于2个与前面相等的面积
+
2个与右面相等的面积的和。
13.
540
14.
800
15.(1)12
40(2)3
二、1.C
2.A
[提示]在长方体中,相交于一个顶点的棱分别是长方体的长、宽、高,长、宽、高的和的4倍就是棱长总和,相交于一个顶点的所有棱长之和是52
÷
4
=
13(厘米)。
3.A
[提示]把一个长方体切割成3个体积相等的长方体,可以增加4个面,表面积最多可增
加9
×
6
×
4
=
216(平方厘米)。
4.B
[提示]这个长方体的长是4分米,宽是3分米,高是2分米。
5.B
6.B
7.D
8.C
三、1.√
2.√
3.
×
[提示]把两个完全一样的正方体拼成一个长方体,体积不变,表面积变了。
4.
×
[提示]至少8个完全一样的小正方体才能拼成一个较大的正方体。
5.
×
四、1.(1)384
dm2
512
dm3
(2)58
m2
28
m3
2.(1)V
=
10
×
5
×
3
+
4
×
4
×
4
=
214(cm3)
(2)V
=
5
×
5
×
5
-
2
×
2
×
3
=
113(cm3)
3.104立方厘米
[提示]用两个完全一样的立体图形可以拼成一个长为13厘米,宽为4厘米,高为4厘米的长方体,求出长方体的体积再除以2得出所求图形的体积。列式是(9
+
4)×
4
×
4
÷
2
=
104(立方厘米)。
五、1.(1)(50
+
25)×
2
=
150(米)[提示]求红色线长多少米,就是求游泳池上面的周长。
(2)50
×
25
+
50
×
1.5
×
2
+
25
×
1.5
×
2
=
1475(平方米)
(3)50
×
25
×(1.5
-
0.2)
=
1625(立方米)
2.
1.2
×
0.5
+(1.2
+
0.5)×
0.8
×
2
=
3.32(平方米)[提示]求做这样一个木箱至少需要多少平方米的木料,就是求木箱前、后、左、右和下面5个面的面积之和。
3.
18
×
13
×
25
÷
50
=
117(立方厘米)
4.
4
×
2.5
×
1.2
=
12(立方分米)
[提示]水面上升部分的体积就是铁块的体积。
5.
高:440
÷
4
÷(1
+
1.5
+
1.5
×
2)=
20(厘米)
宽:20
×
1.5
=
30(厘米)
长:30
×
2
=
60(厘米)
6.10
×
10
×
9
÷(15
×
10)=
6(厘米)[提示]本题考查长方体的体积计算。长方体的体积
=
长
×
宽
×
高,长方体的体积
=
底面积
×
高。长方体按第一个图形所示放置时,长为10厘米,宽为10厘米,水高9厘米,水的体积:10
×
10
×
9
=
900(立方厘米);按第二个图形所示放置时,水的体积不变,依旧是900立方厘米,长为15厘米,宽为10厘米,底面积为15
×
10
=
150(平方厘米),水的高度:900
÷
150
=
6(厘米),所以水面的高度是6厘米。
精挑好题
(1)48
80
[提示]拼成的大长方体的长是4厘米、宽是3厘米、高是4厘米。
(2)20
16
(时间:60分钟总分:100分)
一、填一填。(每空1分,共26分)
1.(1)一个梨的体积约是115( )。
(2)一只铝锅能盛5( )水。
(3)一个仓库的容积约是220( )。
(4)
一个茶杯可以装水500( )。
2.
250立方分米
=
( )立方米
0.8升
=
( )立方厘米
2立方米30立方分米
=
( )立方米
3.(2020·无锡惠山区期末)一个长方体工艺盒(如右图),框架由铝合金条制成,各个面都用灯箱布围成。制成这个工艺盒,至少需要铝合金条( )厘米;需要灯箱布( )平方厘米(接头处不计);如果工艺盒里面放一些棱长3厘米的正方体木块,最多能放( )块。
4.(2020·福建宁随市期末)一个棱长为1分米的正方体,切割成棱长为1厘米的小正方体,把这些小正方体摆成一行长为( )米。
5.至少需要( )厘米长的铁丝,才能做一个底面周长是18厘米,高是3厘米的长方体框架。
6.把一个棱长是4厘米的正方体切成两个长方体,它的表面积增加了( )平方厘米。
7.把一个长方体切成三个一样的正方体,表面积增加40平方厘米,原来长方体的表面积是
( )平方厘米。
8.一张长方形纸的长是40厘米、宽是8厘米。把它对折、再对折。打开后,就能围成一个高是8厘米的长方体的侧面。如果要为这个长方体配一个底面,那么这个底面的面积是( )平方厘米,围成长方体的体积是( )立方厘米。
9.左下图是一个长方体纸盒的展开图(单位:dm),这个纸盒的用料面积是( )dm2。
10.将2升水倒入右上图中的两个长方体水槽中,使它们的水面高度相等,这个高度是( )厘米。(单位:厘米)
11.在一个长9分米、宽8分米、高7分米的长方体木盒内,最多可以放入( )个棱长为2分米的小正方体木块。
12.(2020·淮安淮安区期末)右图所示的长方体体积是( )立方
厘米,如果沿虚线切开,那么表面积比原来增加( )平方厘米。
13.若把一块不规则的铁块全部浸入底面积为180平方厘米的长方体鱼缸中,水面上升了3厘米且水未溢出,则这块铁块的体积是( )立方厘米。
14.一个棱长1米的正方体水池,蓄水的水面低于池口2分米,池内蓄水( )升。
15.(2020·南京江宁区期末)(1)右图中,小正方体的棱长为1厘米,这个立体图形的体积是( )立方厘米;表面积是( )平方厘米。
(2)至少移动其中( )个小正方体可以将这个立体图形变成一个体积不变的长方体。
二、选一选。(每题1分,共8分)
1.(2020·淮安淮安区期末)下面不能沿虚线折成正方体的是( )。
2.一个长方体的棱长之和是52厘米,相交于一个顶点的所有棱长之和是( )。
A.13厘米
B.15厘米
C.14厘米
D.16厘米
3.(2020·无锡惠山区期末)一个长9厘米、宽6厘米、高3厘米的长方体,切割成3个体积相等的长方体,表面积最多可增加( )平方厘米。
A.216
B.108
C.72
D.36
(2020·淮安淮安区期末)小红用一些1
dm3的
小正方体摆成一个长方体,从正面、左面和上面
看到的图形分别如右图所示,这个长方体的体积是( )dm3。
A.52
B.24
C.18
5.将一块长为5分米、宽为6分米、高为0.3米的长方体木料,锯成棱长是1分米的小正方体,可以锯成( )。
A.9块
B.90块
C.18块
D.180块
6.把一块体积为20立方厘米的铁块沉入一个底面长为5厘米、宽为2厘米的长方体玻璃容器中,水面会上升( )。(铁块完全浸没在水中且水未溢出)
A.20厘米
B.2厘米
C.4厘米
D.无法确定
7.一个长方体的盒子,从里面量,长8分米、宽5分米、高4分米。如果把棱长为2分米的正方体木块放到这个盒子里,那么最多能放( )。
A.12个
B.14个
C.20个
D.16个
8.将一个长为6厘米、宽为5厘米、高为4厘米的长方体截成一个体积最大的正方体,这个正方体的体积是( )。
A.125立方厘米
B.125平方厘米
C.64立方厘米
D.64平方厘米
三、判一判。(每题1分,共5分)
1.一个正方体的体积是1立方厘米,它的底面周长是4厘米。
(
)
2.表面积相等的两个正方体,它们的体积也相等。
(
)
3.把两个完全一样的正方体拼成一个长方体,体积和表面积都不变。
(
)
4.至少4个完全一样的小正方体才能拼成一个较大的正方体。
(
)
5.如果甲容器的体积比乙容器的体积大,那么甲容器的容积一定比乙容器的容积大。(
)
四、计算题。(第3题5分,其余每题8分,共21分)
1.求下列各图形的表面积和体积。
2.求下列各图形的体积。(单位:cm)(1)(2)
3.张师傅将一个长方体木块平均分成两块,右下图是其中的一部分,请你计算出这部分的体积。(单位:厘米)
五、解决问题。(第1题12分,第2题4分,其余每题6分,共40分)
1.(2020·福建宁德市期末)体育馆修建一座游泳池,游泳池的长是50米,宽是25米,深是1.5米。
(1)沿游泳池口用油漆画一圈红色线,红色线长多少米?
如果在游泳池的底面和四周贴瓷砖,那么贴瓷砖的面积是多少平方米?
(3)如果往游泳池里放水,使水面到池口的距离是0.2米,那么需要多少立方米水?
2.粮店售米用的木箱(无盖)长为1.2米,宽为0.5米,高为0.8米。做这样一个木箱至少需要多少平方米的木料?
3.用50本数学课本摆成一个长是18厘米、宽是13厘米、高是25厘米的长方体,平均每本书的体积是多少立方厘米?
4.一个长方体容器,长为4分米,宽为2.5分米,高为3分米,一个铁块完全浸入水中后(水未溢出),水面升高了1.2分米。这个铁块的体积是多少?
5.一个长方体的棱长总和是440厘米,已知长是宽的2倍,宽是高的1.5倍。这个长方体的长、宽、高分别是多少厘米?
6.一个封闭的长方体容器,长、宽、高分别是10厘米、10厘米和15厘米。长方体容器里面装着水,张明不小心把容器碰倒了。
精挑好题。
(2020·南通如东县期末)右图是用棱长为1厘米的小正方体拼成的大长方体。
(1)拼成这个图形用了( )个小正方体,拼成图形的表面积是(
)平方厘米。
(2)给拼成图形的表面涂色后,再全都分开,其中两面涂色的有( )块,一面涂色的有( )块。
第一单元综合提优测评卷(B)
1.(1)立方厘米
(2)升
(3)立方米
(4)毫升
2.
0.25
800
2.03
[提示]把高级单位的名数改写成低级单位的名数,用高级单位前面的数乘进率。把低级单位的名数改写成高级单位的名数,用低级单位前面的数除以进率。
3.
220
1800
150
[提示]长方体中有4条长、4条宽、4条高,求至少需要铝条多少厘米,就是求棱长总和,列式是(15
+
10
+
30)×
4
=
220(厘米)。
4.
10
5.48
6.
32
[提示]把一个棱长是4厘米的正方体切成两个长方体,表面积增加了2个与原正方形右面相等的正方形,所以它的表面积增加了4
×
4
×
2
=
32(平方厘米)。
7.
140
8.
100
800
9.
88
10.
12.5
11.
48
[提示]把棱长为2分米的小正方体木块放入长方体木盒内,密放后组成的长方体的长、宽、高都是2的倍数,9
÷
2
=
4(个)…1(分米),8
÷
2
=
4(个),7
÷
2
=
3(个)…1(分米),放的个数为4
×
4
×
3
=
48(个)。
12.
120
88
[提示]看图可以发现表面积比原来增加的面积等于2个与前面相等的面积
+
2个与右面相等的面积的和。
13.
540
14.
800
15.(1)12
40(2)3
二、1.C
2.A
[提示]在长方体中,相交于一个顶点的棱分别是长方体的长、宽、高,长、宽、高的和的4倍就是棱长总和,相交于一个顶点的所有棱长之和是52
÷
4
=
13(厘米)。
3.A
[提示]把一个长方体切割成3个体积相等的长方体,可以增加4个面,表面积最多可增
加9
×
6
×
4
=
216(平方厘米)。
4.B
[提示]这个长方体的长是4分米,宽是3分米,高是2分米。
5.B
6.B
7.D
8.C
三、1.√
2.√
3.
×
[提示]把两个完全一样的正方体拼成一个长方体,体积不变,表面积变了。
4.
×
[提示]至少8个完全一样的小正方体才能拼成一个较大的正方体。
5.
×
四、1.(1)384
dm2
512
dm3
(2)58
m2
28
m3
2.(1)V
=
10
×
5
×
3
+
4
×
4
×
4
=
214(cm3)
(2)V
=
5
×
5
×
5
-
2
×
2
×
3
=
113(cm3)
3.104立方厘米
[提示]用两个完全一样的立体图形可以拼成一个长为13厘米,宽为4厘米,高为4厘米的长方体,求出长方体的体积再除以2得出所求图形的体积。列式是(9
+
4)×
4
×
4
÷
2
=
104(立方厘米)。
五、1.(1)(50
+
25)×
2
=
150(米)[提示]求红色线长多少米,就是求游泳池上面的周长。
(2)50
×
25
+
50
×
1.5
×
2
+
25
×
1.5
×
2
=
1475(平方米)
(3)50
×
25
×(1.5
-
0.2)
=
1625(立方米)
2.
1.2
×
0.5
+(1.2
+
0.5)×
0.8
×
2
=
3.32(平方米)[提示]求做这样一个木箱至少需要多少平方米的木料,就是求木箱前、后、左、右和下面5个面的面积之和。
3.
18
×
13
×
25
÷
50
=
117(立方厘米)
4.
4
×
2.5
×
1.2
=
12(立方分米)
[提示]水面上升部分的体积就是铁块的体积。
5.
高:440
÷
4
÷(1
+
1.5
+
1.5
×
2)=
20(厘米)
宽:20
×
1.5
=
30(厘米)
长:30
×
2
=
60(厘米)
6.10
×
10
×
9
÷(15
×
10)=
6(厘米)[提示]本题考查长方体的体积计算。长方体的体积
=
长
×
宽
×
高,长方体的体积
=
底面积
×
高。长方体按第一个图形所示放置时,长为10厘米,宽为10厘米,水高9厘米,水的体积:10
×
10
×
9
=
900(立方厘米);按第二个图形所示放置时,水的体积不变,依旧是900立方厘米,长为15厘米,宽为10厘米,底面积为15
×
10
=
150(平方厘米),水的高度:900
÷
150
=
6(厘米),所以水面的高度是6厘米。
精挑好题
(1)48
80
[提示]拼成的大长方体的长是4厘米、宽是3厘米、高是4厘米。
(2)20
16
