2021-2022学年人教版八年级数学上册第十二章 全等三角形 12.2三角形全等的判定(第二课时)课件(共25张PPT)
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册第十二章 全等三角形 12.2三角形全等的判定(第二课时)课件(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-31 08:53:38 | ||
图片预览






文档简介
(共25张PPT)
第十二章
全等三角形
12.2
三角形全等的判定
第二课时
【学习目标】
1.理解和掌握全等三角形判定方法2——“SAS”.理解满足“SSA”的两个三角形不一定全等.
2.能把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等.
3.能运用“SAS”证明简单的三角形全等问题。
【课前预习】
1.在△ABC和△DEF中,下列给出的条件,能用“SAS”判定这两个三角形全等的是(
)
A.AB=DE,BC=DF,∠A=∠D
B.AB=BC,DE=EF,∠B=∠E
C.AB=EF,AC=DF,∠A=∠D
D.BC=EF,AC=DF,∠C=∠F
2..如图,在△ABC中,AD平分∠BAC,且AE=AF,则可直接
用“SAS”判断的是( )
A.△ABD≌△ACDB.△BDE≌△CDF
C.△ADE≌△ADFD.△ABD≌△ABC
3.下列条件能判定△ABC≌△DEF的是( )
A.AB=DE
AC=DF
∠B=∠E
B.AB=DE
AC=DF
∠C=∠F
C.AB=DE
AC=DF
∠A=∠D
D.AB=DE
AC=DF
∠B=∠F
4.下列说法正确的是(
)
A.三角形的两边和第三边上的中线对应相等的两个三角形全等B.三角形的两边和第三边上的高对应相等的两个三角形全等C.三角形的两边和这两边夹角平分线对应相等的两个三角形全等D.三角形的两边和这两边所成的对应的外角平分线对应相等的两个三角形
5.下列判断正确的个数是(
)
①两个正三角形一定是全等图形;②三角形的一个外角一定大于与它不相邻的一个内角;③三角形的三条高一定交于同一点;④两边和一角对应相等的两个三角形全等.
A.3个
B.2个
C.1个
D.0个
【课前预习】答案
1.C
2.C
3.C
4.C
5.C
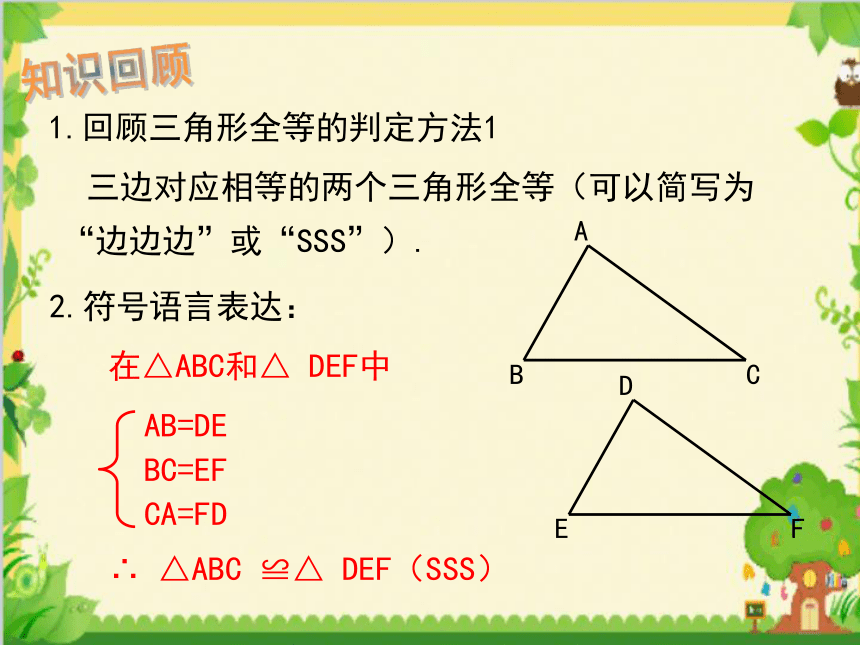
1.回顾三角形全等的判定方法1
三边对应相等的两个三角形全等(可以简写为
“边边边”或“SSS”).
在△ABC和△
DEF中
∴
△ABC
≌△
DEF(SSS)
AB=DE
BC=EF
CA=FD
2.符号语言表达:
A
B
C
D
E
F
知识回顾
继续探索三角形全等的条件.
(2)
三条边
(1)
三个角
(3)
两边一角
(4)
两角一边
当两个三角形满足六个条件中的三个时,有四种情况:
SSS
不能!
?
学习探究
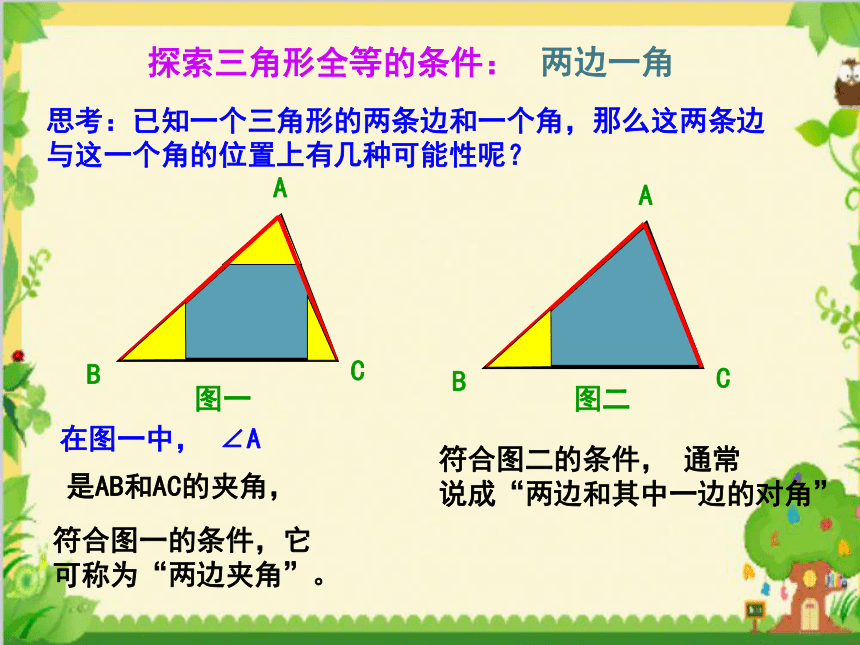
探索三角形全等的条件:
两边一角
思考:已知一个三角形的两条边和一个角,那么这两条边
与这一个角的位置上有几种可能性呢?
A
B
C
A
B
C
图一
图二
在图一中,
∠A
是AB和AC的夹角,
符合图一的条件,它可称为“两边夹角”。
符合图二的条件,
通常
说成“两边和其中一边的对角”
问题1 先任意画出一个△ABC,再画一个△A′B′C′,使A′B′
=AB,∠A′=∠A,C′A′=
CA(即两边和它们的夹角分别相等).把画好的△A′B′C′剪下来,放到△ABC
上,它们全等吗?
探究
三角形全等的判定(“边角边”定理)
一
A
B
C
A′
D
E
B′
C′
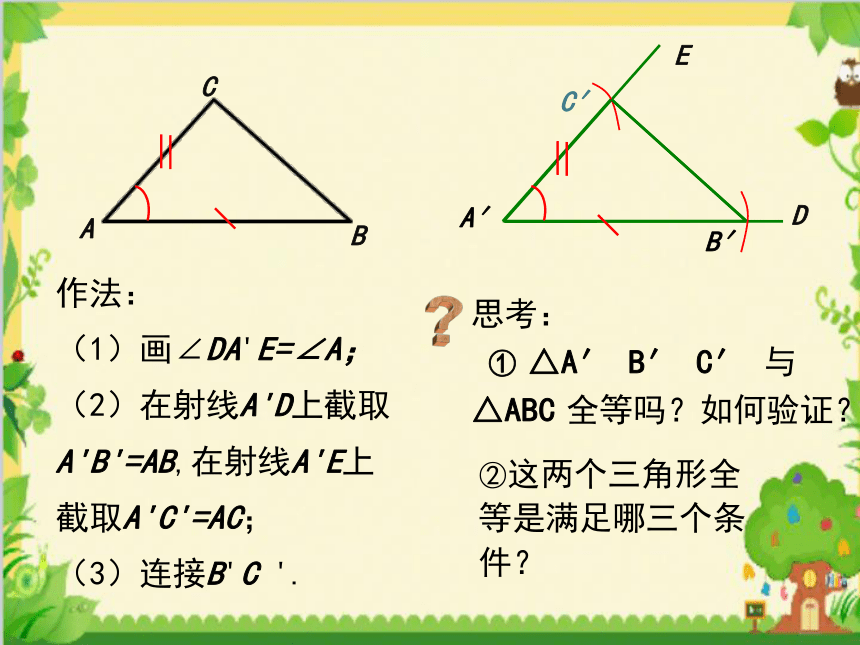
作法:
(1)画∠DA'E=∠A;
(2)在射线A'D上截取A'B'=AB,在射线A'E上截取A'C'=AC;
(3)连接B'C
'.
?
思考:
①
△A′
B′
C′
与
△ABC
全等吗?如何验证?
②这两个三角形全等是满足哪三个条件?
在△ABC
和△
DEF中,
∴ △ABC
≌△
DEF(SAS).
文字语言:两边和它们的夹角分别相等的两个三角形全等
(简写成“边角边”或“SAS
”).
“边角边”判定方法
几何语言:
AB
=
DE,
∠A
=∠D,
AC
=AF
,
A
B
C
D
E
F
必须是两边“夹角”
归纳
例1
如果AB=CB
,∠
ABD=
∠
CBD,那么
△
ABD
和△
CBD
全等吗?
分析:
△
ABD
≌△
CBD.
边:
角:
边:
AB=CB(已知),
∠ABD=
∠CBD(已知),
?
A
B
C
D
(SAS)
BD=BD(公共边).
A
B
C
D
证明:
在△ABD
和△
CBD中,
AB=CB(已知),
∠ABD=
∠CBD(已知),
BD=BD(公共边),
∴
△
ABD
≌△
CBD
(
SAS).
想一想:
现在例1的已知条件不改变,而问题改变成:
问AD=CD吗?BD平分∠ADC吗?
由△
ABD
≌△
CBD可得AD=CD(全等三角形的对应边相等),BD平分∠ADC(全等三角形的对应角相等,∠ADB=∠CDB).
变式1:
已知:如图,AB=CB,∠1=
∠2.
求证:(1)
AD=CD;
(2)
DB
平分∠
ADC.
A
D
B
C
1
2
4
3
在△ABD与△CBD中,
证明:
∴△ABD≌△CBD(SAS),
AB=CB
(已知),
∠1=∠2
(已知),
BD=BD
(公共边),
∴AD=CD,∠3=∠4,
∴DB
平分∠
ADC.
A
B
C
D
变式2:
已知:AD=CD,DB平分∠ADC
,求证:∠A=∠C.
1
2
在△ABD与△CBD中,
证明:
∴△ABD≌△CBD(SAS),
AD=CD
(已知),
∠1=∠2
(已证),
BD=BD
(公共边),
∴∠A=∠C.
∵DB
平分∠
ADC,
∴∠1=∠2.
问题2 某同学不小心把一块三角形的玻璃从两个顶点处打碎成两块(如图),现要到玻璃店去配一块完全一样的玻璃.请问如果只准带一块碎片,应该带哪一块去,能试着说明理由吗?
二
“SAS”判定方法的应用
利用今天所学“边角边”知识,带黑色的那块.因
为它完整地保留了两边及其夹角,一个三角形两条边的长度和夹角的大小确定了,这个三角形的形状、大小就确定下来了.
例2
如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长到点D,使CD=CA,连接BC并延长到点E,使CE=CB.连接DE,那么量出DE的长就是A、B的距离,为什么?
C
·
A
E
D
B
分析:
如果能证明△ABC≌
△DEC,
就可以得出AB=DE.由题意知,
△ABC和△DEC具备“边角边”的条件.
证明:在△ABC
和△DEC
中,
∴△ABC
≌△DEC(SAS).
∴AB
=DE
(全等三角形的对应边相等).
AC
=
DC(已知),
∠1
=∠2
(对顶角相等),
CB=EC(已知)
,
C
·
A
E
D
B
1
2
证明线段相等或者角相等时,常常通过证明它们是全等三角形的对应边或对应角来解决.
归纳
如图,在△ABC
和△ABD
中,
AB
=AB,AC
=
AD,∠B
=∠B,
但△ABC
和△ABD
不全等.
问题3
两边一角分别相等包括“两边夹角”和“两边及其中一边的对角”分别相等两种情况,前面已探索出“SAS”判定三角形全等的方法,那么由“SSA”的条件能判定两个三角形全等吗?
A
B
C
D
三、探索“SSA”能否识别两三角形全等
画△ABC
和△DEF,使∠B
=∠E
=30°,
AB
=DE=5
cm
,AC
=DF
=3
cm
.观察所得的两个三角形是否全等?
两边和其中一边的对角对应相等这三个条件无法唯一确定三角形的形状,所以不能保证两个三角形全等.因此,△ABC
和△DEF
不一定全等.
例3
下列条件中,不能证明△ABC≌△DEF的是( )
A.AB=DE,∠B=∠E,BC=EF
B.AB=DE,∠A=∠D,AC=DF
C.BC=EF,∠B=∠E,AC=DF
D.BC=EF,∠C=∠F,AC=DF
解析:要判断能不能使△ABC≌△DEF,应看所给出的条件是不是两边和这两边的夹角,只有选项C的条件不符合,故选C.
C
方法总结:判断三角形全等时,注意两边与其中一边的对角相等的两个三角形不一定全等.解题时要根据已知条件的位置来考虑,只具备SSA时是不能判定三角形全等的.
课堂小结
边角边
内容
有两边及夹角对应相等的两个三角形全等(简写成
“SAS”)
应用
为证明线段和角相等提供了新的证法
注意
1.已知两边,必须找“夹角”
2.
已知一角和这角的一夹边,必须找这角的另一夹边
【课后练习】
1.对于如下命题:①直角三角形两锐角互余.②若两个角相等,则它们是对顶角.③两点之间,线段最短.④两边及夹角分别相等的两个三角形全等.假命题是(
)
A.①
B.②
C.③
D.④
2.在△ABC和△A?B?C?中,下列条件:①∠A=∠A?;②∠B=∠B?;③∠C=∠C?;④AB=A?B?;⑤AC=A?C?;⑥BC=B?C?,其中,能用“SAS”证明△ABC≌△A?B?C?的一组是(
)
A.①⑤⑥
B.②④⑤
C.①④⑥
D.②④⑥
3.下列命题正确的是(
)
A.三角形的一个外角大于任何一个内角B.三角形的三条高都在三角形内部C.三角形的一条中线将三角形分成两个三角形面积相等D.两边和其中一边的对角相等的三角形全等
4.在△ABC和△A′B′C′中:①AB=A′B′②BC=B′C′③AC=A′C′④∠A=∠A′⑤∠B=∠B′.则下列条件中,不能保证△ABC≌△A′B′C′的是(
)
A.①②③
B.①②⑤
C.①③④
D.①③⑤
5.下列结论正确的个数有(
)
①有两边和一角对应相等的两个三角形全等;②三角形三边的垂直平分线相交于一点;③有两边及夹角对应相等的两个三角形全等;④三角形三个内角的角平分线有可能相交于三角形的外部.
A.0个
B.1个
C.2个
D.3个
6.△ABC和△ADC中,下列三个论断:①AB=AD;②∠BAC=∠DAC;③BC=DC.将两个论断作为条件,另一个论断作为结论构成一个命题,写出一个真命题:__________.
7.已知△ABC的边AB=3,AC=5,那么边BC上的中线AD的范围为___.
8.如图,在△DCA与△DEB中,有以下四个等式①DE=DC;②DA=DB;③∠C=∠E;④AC=BE,请以其中三个等式作条件,余下一个作结论,写出所有的正确判断
___________________________(用
形式表示)
9.如图,点E,F在线段AD上,且AE=DF,AB∥DC,AB=DC,连接BE,BF,CE,CF,则图中共有_____对全等三角形.
10.已知:如图,在长方形ABCD中,AB=6,AD=10,延长BC到点E,使CE=4,连接DE,动点F从点B出发,以每秒2个单位长度的速度沿BC-CD-DA向终点A运动,设点F的运动时间为t秒,当t的值为_______时,△ABF和△DCE全等.
【课后练习】答案
1.B
2.D
3.C
4.D
5.C
【课后练习】
1.D
2.C
3.C
4.C
5.C
6.①②
③
7.1<AD<4
8.①②④
③,①④③
②.
9.3
10.2或11
第十二章
全等三角形
12.2
三角形全等的判定
第二课时
【学习目标】
1.理解和掌握全等三角形判定方法2——“SAS”.理解满足“SSA”的两个三角形不一定全等.
2.能把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等.
3.能运用“SAS”证明简单的三角形全等问题。
【课前预习】
1.在△ABC和△DEF中,下列给出的条件,能用“SAS”判定这两个三角形全等的是(
)
A.AB=DE,BC=DF,∠A=∠D
B.AB=BC,DE=EF,∠B=∠E
C.AB=EF,AC=DF,∠A=∠D
D.BC=EF,AC=DF,∠C=∠F
2..如图,在△ABC中,AD平分∠BAC,且AE=AF,则可直接
用“SAS”判断的是( )
A.△ABD≌△ACDB.△BDE≌△CDF
C.△ADE≌△ADFD.△ABD≌△ABC
3.下列条件能判定△ABC≌△DEF的是( )
A.AB=DE
AC=DF
∠B=∠E
B.AB=DE
AC=DF
∠C=∠F
C.AB=DE
AC=DF
∠A=∠D
D.AB=DE
AC=DF
∠B=∠F
4.下列说法正确的是(
)
A.三角形的两边和第三边上的中线对应相等的两个三角形全等B.三角形的两边和第三边上的高对应相等的两个三角形全等C.三角形的两边和这两边夹角平分线对应相等的两个三角形全等D.三角形的两边和这两边所成的对应的外角平分线对应相等的两个三角形
5.下列判断正确的个数是(
)
①两个正三角形一定是全等图形;②三角形的一个外角一定大于与它不相邻的一个内角;③三角形的三条高一定交于同一点;④两边和一角对应相等的两个三角形全等.
A.3个
B.2个
C.1个
D.0个
【课前预习】答案
1.C
2.C
3.C
4.C
5.C
1.回顾三角形全等的判定方法1
三边对应相等的两个三角形全等(可以简写为
“边边边”或“SSS”).
在△ABC和△
DEF中
∴
△ABC
≌△
DEF(SSS)
AB=DE
BC=EF
CA=FD
2.符号语言表达:
A
B
C
D
E
F
知识回顾
继续探索三角形全等的条件.
(2)
三条边
(1)
三个角
(3)
两边一角
(4)
两角一边
当两个三角形满足六个条件中的三个时,有四种情况:
SSS
不能!
?
学习探究
探索三角形全等的条件:
两边一角
思考:已知一个三角形的两条边和一个角,那么这两条边
与这一个角的位置上有几种可能性呢?
A
B
C
A
B
C
图一
图二
在图一中,
∠A
是AB和AC的夹角,
符合图一的条件,它可称为“两边夹角”。
符合图二的条件,
通常
说成“两边和其中一边的对角”
问题1 先任意画出一个△ABC,再画一个△A′B′C′,使A′B′
=AB,∠A′=∠A,C′A′=
CA(即两边和它们的夹角分别相等).把画好的△A′B′C′剪下来,放到△ABC
上,它们全等吗?
探究
三角形全等的判定(“边角边”定理)
一
A
B
C
A′
D
E
B′
C′
作法:
(1)画∠DA'E=∠A;
(2)在射线A'D上截取A'B'=AB,在射线A'E上截取A'C'=AC;
(3)连接B'C
'.
?
思考:
①
△A′
B′
C′
与
△ABC
全等吗?如何验证?
②这两个三角形全等是满足哪三个条件?
在△ABC
和△
DEF中,
∴ △ABC
≌△
DEF(SAS).
文字语言:两边和它们的夹角分别相等的两个三角形全等
(简写成“边角边”或“SAS
”).
“边角边”判定方法
几何语言:
AB
=
DE,
∠A
=∠D,
AC
=AF
,
A
B
C
D
E
F
必须是两边“夹角”
归纳
例1
如果AB=CB
,∠
ABD=
∠
CBD,那么
△
ABD
和△
CBD
全等吗?
分析:
△
ABD
≌△
CBD.
边:
角:
边:
AB=CB(已知),
∠ABD=
∠CBD(已知),
?
A
B
C
D
(SAS)
BD=BD(公共边).
A
B
C
D
证明:
在△ABD
和△
CBD中,
AB=CB(已知),
∠ABD=
∠CBD(已知),
BD=BD(公共边),
∴
△
ABD
≌△
CBD
(
SAS).
想一想:
现在例1的已知条件不改变,而问题改变成:
问AD=CD吗?BD平分∠ADC吗?
由△
ABD
≌△
CBD可得AD=CD(全等三角形的对应边相等),BD平分∠ADC(全等三角形的对应角相等,∠ADB=∠CDB).
变式1:
已知:如图,AB=CB,∠1=
∠2.
求证:(1)
AD=CD;
(2)
DB
平分∠
ADC.
A
D
B
C
1
2
4
3
在△ABD与△CBD中,
证明:
∴△ABD≌△CBD(SAS),
AB=CB
(已知),
∠1=∠2
(已知),
BD=BD
(公共边),
∴AD=CD,∠3=∠4,
∴DB
平分∠
ADC.
A
B
C
D
变式2:
已知:AD=CD,DB平分∠ADC
,求证:∠A=∠C.
1
2
在△ABD与△CBD中,
证明:
∴△ABD≌△CBD(SAS),
AD=CD
(已知),
∠1=∠2
(已证),
BD=BD
(公共边),
∴∠A=∠C.
∵DB
平分∠
ADC,
∴∠1=∠2.
问题2 某同学不小心把一块三角形的玻璃从两个顶点处打碎成两块(如图),现要到玻璃店去配一块完全一样的玻璃.请问如果只准带一块碎片,应该带哪一块去,能试着说明理由吗?
二
“SAS”判定方法的应用
利用今天所学“边角边”知识,带黑色的那块.因
为它完整地保留了两边及其夹角,一个三角形两条边的长度和夹角的大小确定了,这个三角形的形状、大小就确定下来了.
例2
如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长到点D,使CD=CA,连接BC并延长到点E,使CE=CB.连接DE,那么量出DE的长就是A、B的距离,为什么?
C
·
A
E
D
B
分析:
如果能证明△ABC≌
△DEC,
就可以得出AB=DE.由题意知,
△ABC和△DEC具备“边角边”的条件.
证明:在△ABC
和△DEC
中,
∴△ABC
≌△DEC(SAS).
∴AB
=DE
(全等三角形的对应边相等).
AC
=
DC(已知),
∠1
=∠2
(对顶角相等),
CB=EC(已知)
,
C
·
A
E
D
B
1
2
证明线段相等或者角相等时,常常通过证明它们是全等三角形的对应边或对应角来解决.
归纳
如图,在△ABC
和△ABD
中,
AB
=AB,AC
=
AD,∠B
=∠B,
但△ABC
和△ABD
不全等.
问题3
两边一角分别相等包括“两边夹角”和“两边及其中一边的对角”分别相等两种情况,前面已探索出“SAS”判定三角形全等的方法,那么由“SSA”的条件能判定两个三角形全等吗?
A
B
C
D
三、探索“SSA”能否识别两三角形全等
画△ABC
和△DEF,使∠B
=∠E
=30°,
AB
=DE=5
cm
,AC
=DF
=3
cm
.观察所得的两个三角形是否全等?
两边和其中一边的对角对应相等这三个条件无法唯一确定三角形的形状,所以不能保证两个三角形全等.因此,△ABC
和△DEF
不一定全等.
例3
下列条件中,不能证明△ABC≌△DEF的是( )
A.AB=DE,∠B=∠E,BC=EF
B.AB=DE,∠A=∠D,AC=DF
C.BC=EF,∠B=∠E,AC=DF
D.BC=EF,∠C=∠F,AC=DF
解析:要判断能不能使△ABC≌△DEF,应看所给出的条件是不是两边和这两边的夹角,只有选项C的条件不符合,故选C.
C
方法总结:判断三角形全等时,注意两边与其中一边的对角相等的两个三角形不一定全等.解题时要根据已知条件的位置来考虑,只具备SSA时是不能判定三角形全等的.
课堂小结
边角边
内容
有两边及夹角对应相等的两个三角形全等(简写成
“SAS”)
应用
为证明线段和角相等提供了新的证法
注意
1.已知两边,必须找“夹角”
2.
已知一角和这角的一夹边,必须找这角的另一夹边
【课后练习】
1.对于如下命题:①直角三角形两锐角互余.②若两个角相等,则它们是对顶角.③两点之间,线段最短.④两边及夹角分别相等的两个三角形全等.假命题是(
)
A.①
B.②
C.③
D.④
2.在△ABC和△A?B?C?中,下列条件:①∠A=∠A?;②∠B=∠B?;③∠C=∠C?;④AB=A?B?;⑤AC=A?C?;⑥BC=B?C?,其中,能用“SAS”证明△ABC≌△A?B?C?的一组是(
)
A.①⑤⑥
B.②④⑤
C.①④⑥
D.②④⑥
3.下列命题正确的是(
)
A.三角形的一个外角大于任何一个内角B.三角形的三条高都在三角形内部C.三角形的一条中线将三角形分成两个三角形面积相等D.两边和其中一边的对角相等的三角形全等
4.在△ABC和△A′B′C′中:①AB=A′B′②BC=B′C′③AC=A′C′④∠A=∠A′⑤∠B=∠B′.则下列条件中,不能保证△ABC≌△A′B′C′的是(
)
A.①②③
B.①②⑤
C.①③④
D.①③⑤
5.下列结论正确的个数有(
)
①有两边和一角对应相等的两个三角形全等;②三角形三边的垂直平分线相交于一点;③有两边及夹角对应相等的两个三角形全等;④三角形三个内角的角平分线有可能相交于三角形的外部.
A.0个
B.1个
C.2个
D.3个
6.△ABC和△ADC中,下列三个论断:①AB=AD;②∠BAC=∠DAC;③BC=DC.将两个论断作为条件,另一个论断作为结论构成一个命题,写出一个真命题:__________.
7.已知△ABC的边AB=3,AC=5,那么边BC上的中线AD的范围为___.
8.如图,在△DCA与△DEB中,有以下四个等式①DE=DC;②DA=DB;③∠C=∠E;④AC=BE,请以其中三个等式作条件,余下一个作结论,写出所有的正确判断
___________________________(用
形式表示)
9.如图,点E,F在线段AD上,且AE=DF,AB∥DC,AB=DC,连接BE,BF,CE,CF,则图中共有_____对全等三角形.
10.已知:如图,在长方形ABCD中,AB=6,AD=10,延长BC到点E,使CE=4,连接DE,动点F从点B出发,以每秒2个单位长度的速度沿BC-CD-DA向终点A运动,设点F的运动时间为t秒,当t的值为_______时,△ABF和△DCE全等.
【课后练习】答案
1.B
2.D
3.C
4.D
5.C
【课后练习】
1.D
2.C
3.C
4.C
5.C
6.①②
③
7.1<AD<4
8.①②④
③,①④③
②.
9.3
10.2或11
