综合测试-【新教材】人教B版(2019)高中数学必修第二册练习(Word含答案解析)
文档属性
| 名称 | 综合测试-【新教材】人教B版(2019)高中数学必修第二册练习(Word含答案解析) |  | |
| 格式 | doc | ||
| 文件大小 | 372.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-29 15:49:10 | ||
图片预览




文档简介
第五章综合测试
(时间:120分钟 满分150分)
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.老师为研究男女同学数学学习的差异情况,对某班50名同学(其中男同学30名,女同学20名)采取分层抽样的方法,抽取一个容量为10的样本进行研究,则女同学甲被抽到的概率为( )
A.
B.
C.
D.
2.若某校高一年级8个班参加合唱比赛的得分如茎叶图所示,则这组数据的中位数和平均数分别是( )
A.91.5和91.5
B.91.5和92
C.91和91.5
D.92和92
3.学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n且支出在[20,60)元的样本,其频率分布直方图如图所示,根据此图估计学生在课外读物方面的支出费用的中位数为( )元( )
A.45
B.
C.
D.46
4.下列说法中,正确的是( )
A.数据5,4,4,3,5,2的众数是4
B.一组数据的标准差的平方是这组数据的方差
C.数据2,3,4,5的方差是数据4,6,8,10的方差的一半
D.频率分布直方图中各小矩形的面积等于相应各组的频数
5.从10个事件中任取一个事件,若这个事件是必然事件的概率为0.2,是不可能事件的概率为0.3,则这10个事件中随机事件的个数是( )
A.3
B.4
C.5
D.6
6.口袋内有一些大小相同的红球、黄球和白球,从中任意摸出一球,摸出的球是红球或黄球的概率为0.4,摸出的球是红球或白球的概率为0.9,那么摸出的球是黄球或白球的概率为( )
A.0.7
B.0.5
C.0.3
D.0.6
7.在5件产品中,有3件一等品和2件二等品,从中任取2件,以为概率的事件是( )
A.恰有2件一等品
B.至少有一件一等品
C.至多有一件一等品
D.都不是一等品
8.甲、乙两位同学各拿出6张游戏牌,用作投骰子的奖品,两人商定:骰子朝上的面的点数为奇数时甲得1分,否则乙得1分,先积得3分者获胜,得所有12张游戏牌,并结束游戏.比赛开始后,甲积2分,乙积1分,这时因意外事件中断游戏,以后他们不想再继续这场游戏,下面对这12张游戏牌的分配合理的是( )
A.甲得9张,乙得3张
B.甲得6张,乙得6张
C.甲得8张,乙得4张
D.甲得10张,乙得2张
二、多项选择题(本大题共4小题,每小题5分,共20分,在每小题给出的四个选项中,有多项是符合题目要求的.全部选对的得5分,选对但不全的得3分,有选错的得0分)
9.下列事件中,是随机事件的是( )
A.2021年8月18日,北京市不下雨
B.在标准大气压下,水在4
℃时结冰
C.从标有1,2,3,4的4张号签中任取一张,恰为1号签
D.若x∈R,则x2≥0
10.有甲、乙两种报纸供市民订阅,记事件E为“只订甲报纸”,事件F为“至少订一种报纸”,事件G为“至多订一种报纸”,事件H为“不订甲报纸”,事件I为“一种报纸也不订”.下列命题正确的是( )
A.E与G是互斥事件
B.F与I是互斥事件,且是对立事件
C.F与G不是互斥事件
D.G与I是互斥事件
11.某年级有12个班,现要从2班到12班中选1个班的学生参加一项活动,有人提议:掷两个骰子,得到的点数之和是几就选几班,这种做法( )
A.每个班被选到的概率都为
B.4班和10班被选到的概率都为
C.2班和12班被选到的概率最小
D.7班被选到的概率最大
12.在某地区某高传染性病毒流行期间,为了建立指标显示疫情已受控制,以便向该地区居民显示可以过正常生活,有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”,根据连续7天的新增病例数计算,下列各项中,一定符合上述指标的是( )
A.平均数≤3
B.标准差s≤2
C.平均数≤3且极差小于或等于2
D.众数等于1且极差小于或等于4
三、填空题(本大题共4小题,每小题5分,共20分,把答案填在题中的横线上)
13.某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮练习,每人投10次,投中的次数如下表:
学生
1号
2号
3号
4号
5号
甲班
6
7
7
8
7
乙班
6
7
6
7
9
则以上两组数据的方差中较小的一个为s2=___.
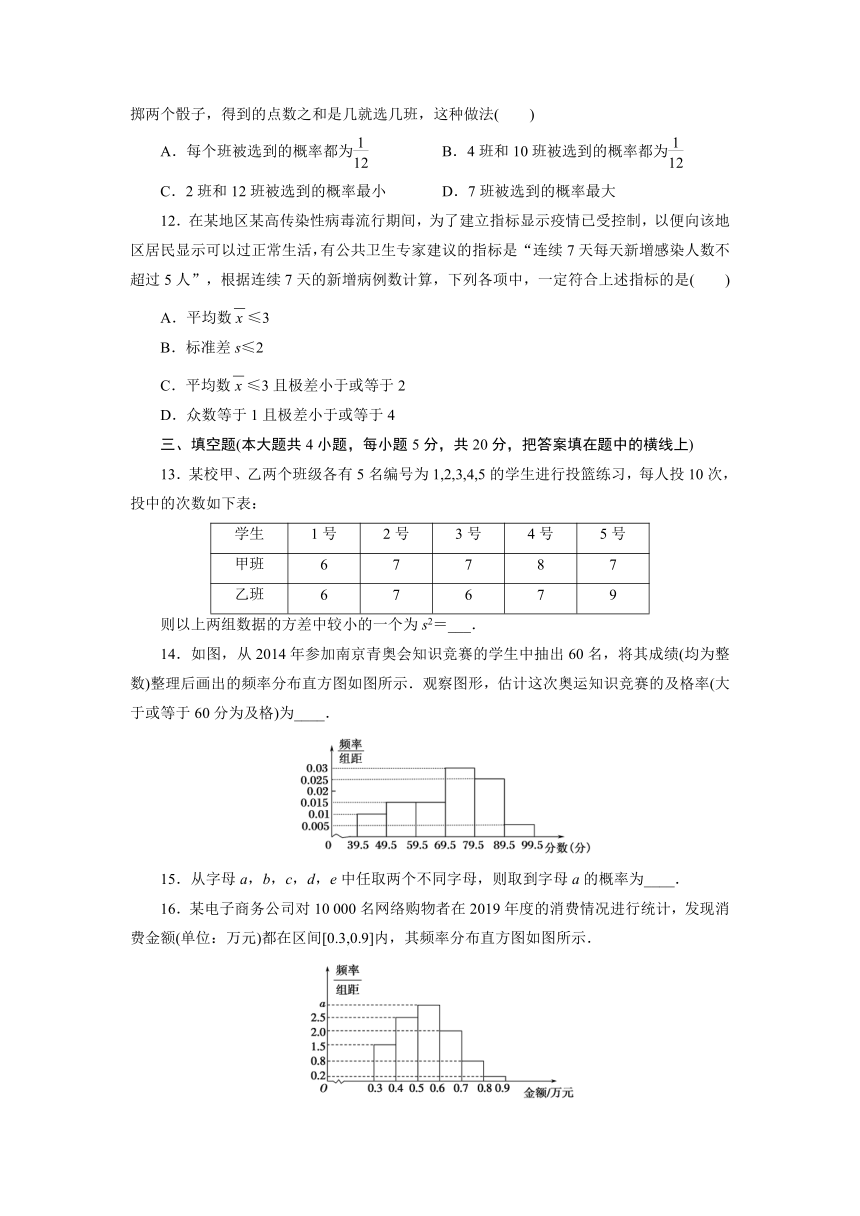
14.如图,从2014年参加南京青奥会知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如图所示.观察图形,估计这次奥运知识竞赛的及格率(大于或等于60分为及格)为____.
15.从字母a,b,c,d,e中任取两个不同字母,则取到字母a的概率为____.
16.某电子商务公司对10
000名网络购物者在2019年度的消费情况进行统计,发现消费金额(单位:万元)都在区间[0.3,0.9]内,其频率分布直方图如图所示.
(1)直方图中的a=____;
(2)在这些购物者中,消费金额在区间[0.5,0.9]内的购物者的人数为____.
四、解答题(本大题共6个小题,共70分,解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分10分)某人去开会,他乘火车、轮船、汽车、飞机去的概率分别为0.3,0.2,0.1,0.4.
(1)求他乘火车或乘飞机去的概率;
(2)若他去的概率为0.5,请问他有可能是乘何种交通工具去的?
18.(本小题满分12分)为了估计一次性木质筷子的用量,2017年从某市共600家高、中、低档饭店中抽取10家进行调查,得到这些饭店每天消耗的一次性筷子盒数分别为0.6,3.7,2.2,1.5,2.8,1.7,2.1,1.2,3.2,1.0.
(1)通过对样本的计算,估计该市2017年共消耗了多少盒一次性筷子.(每年按350个营业日计算)
(2)2019年又对该市一次性木筷的用量以同样的方式做了抽样调查,调查结果是10家饭店平均每家每天使用一次性筷子2.42盒,求该市2018年,2019年这两年一次性木质筷子用量平均每年增长的百分率.
(3)假如让你统计你所在省一年使用一次性木质筷子所消耗的木材量,如何利用统计知识去做?简单地说明你的做法.
19.(本小题满分12分)某班的全体学生共有50人,参加数学测试(百分制)成绩的频率分布直方图如图,数据的分组依次为:[20,40)、[40,60)、[60,80)、[80,100].依此表可以估计这一次测试成绩的中位数为70分.
(1)求表中a、b的值;
(2)请估计该班本次数学测试的平均分.
20.(本小题满分12分)现有6道题,其中4道甲类题,2道乙类题,张同学从中任取2道题解答.试求:
(1)所取的2道题都是甲类题的概率;
(2)所取的2道题不是同一类题的概率.
21.(本小题满分12分)某高中在校学生2
000人,高一年级与高二年级人数相同并且都比高三年级多1人.为了响应市教育局“阳光体育”号召,该校开展了跑步和跳绳两项比赛,要求每人都参加而且只参加其中一项,各年级参与项目人数情况如下表:
年级项目
高一年级
高二年级
高三年级
跑步
a
b
c
跳绳
x
y
z
其中a∶b∶c=2∶3∶5,全校参与跳绳的人数占总人数的.为了了解学生对本次活动的满意度,采用分层抽样从中抽取一个200人的样本进行调查,则高二年级中参与跑步的同学应抽取多少人?
22.(本小题满分12分)砂糖橘是柑橘类的名优品种,因其味甜如砂糖故名.某果农选取一片山地种植砂糖橘,收获时,该果农随机选取果树20株作为样本测量它们每一株的果实产量(单位:kg),获得的所有数据按照区间[40,45],(45,50],(50,55],(55,60]进行分组,得到频率分布直方图如图.已知样本中产量在区间(45,50]上的果树株数是产量在区间(50,60]上的果树株数的倍.
(1)求a、b的值;
(2)从样本中产量在区间(50,60]上的果树里随机抽取两株,求产量在区间(55,60]上的果树至少有一株被抽中的概率.
第五章综合测试
(时间:120分钟 满分150分)
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.老师为研究男女同学数学学习的差异情况,对某班50名同学(其中男同学30名,女同学20名)采取分层抽样的方法,抽取一个容量为10的样本进行研究,则女同学甲被抽到的概率为( C )
A.
B.
C.
D.
[解析] 因为在分层抽样中,任何个体被抽到的概率均相等,所以女同学甲被抽到的概率P==,故应选C.
2.若某校高一年级8个班参加合唱比赛的得分如茎叶图所示,则这组数据的中位数和平均数分别是( A )
A.91.5和91.5
B.91.5和92
C.91和91.5
D.92和92
[解析] 将这组数据从小到大排列,得87、89、90、91、92、93、94、96.
故平均数==91.5,中位数为=91.5,故选A.
3.学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n且支出在[20,60)元的样本,其频率分布直方图如图所示,根据此图估计学生在课外读物方面的支出费用的中位数为( )元( C )
A.45
B.
C.
D.46
[解析] 40+10×=.
4.下列说法中,正确的是( B )
A.数据5,4,4,3,5,2的众数是4
B.一组数据的标准差的平方是这组数据的方差
C.数据2,3,4,5的方差是数据4,6,8,10的方差的一半
D.频率分布直方图中各小矩形的面积等于相应各组的频数
[解析] A中的众数是4和5;C中,2,3,4,5的方差为1.25,而数据4,6,8,10的方差为5;D中,频率分布直方图中各小矩形的面积等于相应各组的频率.
5.从10个事件中任取一个事件,若这个事件是必然事件的概率为0.2,是不可能事件的概率为0.3,则这10个事件中随机事件的个数是( C )
A.3
B.4
C.5
D.6
[解析] 这10个事件中,必然事件的个数为10×0.2=2,不可能事件的个数为10×0.3=3.而必然事件、不可能事件、随机事件是彼此互斥的事件,且它们的个数和为10.故随机事件的个数为10-2-3=5.
6.口袋内有一些大小相同的红球、黄球和白球,从中任意摸出一球,摸出的球是红球或黄球的概率为0.4,摸出的球是红球或白球的概率为0.9,那么摸出的球是黄球或白球的概率为( A )
A.0.7
B.0.5
C.0.3
D.0.6
[解析] 任意摸出一球,事件A=“摸出红球”,事件B=“摸出黄球”,事件C=“摸出白球”,则A、B、C两两互斥.
由题设P(A∪B)=P(A)+P(B)=0.4,
P(A∪C)=P(A)+P(C)=0.9,
又P(A∪B∪C)=P(A)+P(B)+P(C)=1,
∴P(A)=0.4+0.9-1=0.3,
∴P(B∪C)=1-P(A)=1-0.3=0.7.
7.在5件产品中,有3件一等品和2件二等品,从中任取2件,以为概率的事件是( C )
A.恰有2件一等品
B.至少有一件一等品
C.至多有一件一等品
D.都不是一等品
[解析] 将3件一等品编号为1,2,3;2件二等品编号为4,5.从中任取2件有10种取法:(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5).其中恰含有1件一等品的取法有:(1,4),(1,5),(2,4),(2,5),(3,4),(3,5),恰有1件一等品的概率为P1=;恰有2件一等品的取法有:(1,2),(1,3),(2,3),故恰有2件一等品的概率为P2=,其对立事件是“至多有1件一等品”,概率为P3=1-P2=1-=.
8.甲、乙两位同学各拿出6张游戏牌,用作投骰子的奖品,两人商定:骰子朝上的面的点数为奇数时甲得1分,否则乙得1分,先积得3分者获胜,得所有12张游戏牌,并结束游戏.比赛开始后,甲积2分,乙积1分,这时因意外事件中断游戏,以后他们不想再继续这场游戏,下面对这12张游戏牌的分配合理的是( A )
A.甲得9张,乙得3张
B.甲得6张,乙得6张
C.甲得8张,乙得4张
D.甲得10张,乙得2张
[解析] 由题意,得骰子朝上的面的点数为奇数的概率为,即甲、乙每局得分的概率相等,
所以甲获胜的概率是+×=,
乙获胜的概率是×=.
所以甲得到的游戏牌为12×=9(张),乙得到的游戏牌为12×=3(张).
二、多项选择题(本大题共4小题,每小题5分,共20分,在每小题给出的四个选项中,有多项是符合题目要求的.全部选对的得5分,选对但不全的得3分,有选错的得0分)
9.下列事件中,是随机事件的是( AC )
A.2021年8月18日,北京市不下雨
B.在标准大气压下,水在4
℃时结冰
C.从标有1,2,3,4的4张号签中任取一张,恰为1号签
D.若x∈R,则x2≥0
[解析] AC为随机事件,B为不可能事件,D为必然事件.
10.有甲、乙两种报纸供市民订阅,记事件E为“只订甲报纸”,事件F为“至少订一种报纸”,事件G为“至多订一种报纸”,事件H为“不订甲报纸”,事件I为“一种报纸也不订”.下列命题正确的是( BC )
A.E与G是互斥事件
B.F与I是互斥事件,且是对立事件
C.F与G不是互斥事件
D.G与I是互斥事件
[解析] A.E与G不是互斥事件;B.F与I是互斥事件,且是对立事件;C.F与G不是互斥事件;D.G与I不是互斥事件.
11.某年级有12个班,现要从2班到12班中选1个班的学生参加一项活动,有人提议:掷两个骰子,得到的点数之和是几就选几班,这种做法( BCD )
A.每个班被选到的概率都为
B.4班和10班被选到的概率都为
C.2班和12班被选到的概率最小
D.7班被选到的概率最大
[解析] P(1)=0,P(2)=P(12)=,P(3)=P(11)=,P(4)=P(10)=,P(5)=P(9)=,P(6)=P(8)=,P(7)=,故选BCD.
12.在某地区某高传染性病毒流行期间,为了建立指标显示疫情已受控制,以便向该地区居民显示可以过正常生活,有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”,根据连续7天的新增病例数计算,下列各项中,一定符合上述指标的是( CD )
A.平均数≤3
B.标准差s≤2
C.平均数≤3且极差小于或等于2
D.众数等于1且极差小于或等于4
[解析] A中平均数≤3,可能是第一天0人,第二天6人,不符合题意;B中每天感染的人数均为10,标准差也是0,显然不符合题意;C符合,若极差等于0或1,在≤3的条件下,显然符合指标;若极差等于2且≤3,则每天新增感染人数的最小值与最大值有下列可能:(1)0,2,(2)1,3,(3)2,4,符合指标.D符合,若众数等于1且极差小于或等于4,则最大值不超过5,符合指标.
三、填空题(本大题共4小题,每小题5分,共20分,把答案填在题中的横线上)
13.某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮练习,每人投10次,投中的次数如下表:
学生
1号
2号
3号
4号
5号
甲班
6
7
7
8
7
乙班
6
7
6
7
9
则以上两组数据的方差中较小的一个为s2=____.
[解析] 甲=7,s=×(12+02+02+12+02)=;
乙=7,s=×(12+02+12+02+22)=.
∵s<s,∴方差中较小的一个为s,即s2=.
14.如图,从2014年参加南京青奥会知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如图所示.观察图形,估计这次奥运知识竞赛的及格率(大于或等于60分为及格)为__0.75__.
[解析] 及格率为1-(0.01+0.015)×10=0.75.
15.从字母a,b,c,d,e中任取两个不同字母,则取到字母a的概率为____.
[解析] 基本事件总数有10个,即(a,b),(a,c),(a,d),(a,e),(b,c),(b,d),(b,e),(c,d),(c,e),(d,e),其中含a的基本事件有(a,b),(a,c),(a,d),(a,e),共4个,故由古典概型知所求事件的概率P==.
16.某电子商务公司对10
000名网络购物者在2019年度的消费情况进行统计,发现消费金额(单位:万元)都在区间[0.3,0.9]内,其频率分布直方图如图所示.
(1)直方图中的a=__3__;
(2)在这些购物者中,消费金额在区间[0.5,0.9]内的购物者的人数为__6_000__.
[解析] (1)由频率分布直方图及频率和等于1可得0.2×0.1+0.8×0.1+1.5×0.1+2×0.1+2.5×0.1+a×0.1=1,解得a=3.
(2)消费金额在区间[0.5,0.9]内的频率为0.2×0.1+0.8×0.1+2×0.1+3×0.1=0.6,所以消费金额在区间[0.5,0.9]内的购物者的人数为0.6×10
000=6
000.
四、解答题(本大题共6个小题,共70分,解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分10分)某人去开会,他乘火车、轮船、汽车、飞机去的概率分别为0.3,0.2,0.1,0.4.
(1)求他乘火车或乘飞机去的概率;
(2)若他去的概率为0.5,请问他有可能是乘何种交通工具去的?
[解析] 设乘火车去开会为事件A,
乘轮船去开会为事件B,
乘汽车去开会为事件C,
乘飞机去开会为事件D,
则这四个事件是互斥事件.
(1)P(A+D)=P(A)+P(D)=0.3+0.4=0.7.
(2)∵0.5=0.2+0.3=0.1+0.4,
∴他可能乘的交通工具为①火车或轮船,②汽车或飞机.
18.(本小题满分12分)为了估计一次性木质筷子的用量,2017年从某市共600家高、中、低档饭店中抽取10家进行调查,得到这些饭店每天消耗的一次性筷子盒数分别为0.6,3.7,2.2,1.5,2.8,1.7,2.1,1.2,3.2,1.0.
(1)通过对样本的计算,估计该市2017年共消耗了多少盒一次性筷子.(每年按350个营业日计算)
(2)2019年又对该市一次性木筷的用量以同样的方式做了抽样调查,调查结果是10家饭店平均每家每天使用一次性筷子2.42盒,求该市2018年,2019年这两年一次性木质筷子用量平均每年增长的百分率.
(3)假如让你统计你所在省一年使用一次性木质筷子所消耗的木材量,如何利用统计知识去做?简单地说明你的做法.
[解析] (1)样本平均数为=(0.6+3.7+2.2+1.5+2.8+1.7+2.1+1.2+3.2+1.0)==2.
由样本平均数为2估计总体平均数也是2,故2017年该市600家饭店共消耗了一次性筷子为2×350×600=420
000(盒).
(2)由于2017一次性筷子用量是平均每天2盒,而2019年用量是平均每天2.42盒,设平均每年增长的百分率为x,依题意有2.42=2×(1+x)2,解得x=0.1=10%(x=-2.1舍去),所以该市2018年,2019年这两年一次性木质筷子的用量平均每年增长10%.
(3)先采用简单随机抽样的方法抽取若干县(市)(作样本),再从这些县(市)中采用分层抽样的方法抽取若干家饭店,统计一次性木质筷子用量的平均数,从而估计总体平均数,再进一步计算所消耗的木材总量.
19.(本小题满分12分)某班的全体学生共有50人,参加数学测试(百分制)成绩的频率分布直方图如图,数据的分组依次为:[20,40)、[40,60)、[60,80)、[80,100].依此表可以估计这一次测试成绩的中位数为70分.
(1)求表中a、b的值;
(2)请估计该班本次数学测试的平均分.
[解析] (1)由中位数为70可得,
0.005×20+0.01×20+a×10=0.5,
解得a=0.02.
又20(0.005+0.01+0.02+b)=1,
解得b=0.015.
(2)该班本次数学测试的平均分的估计值为30×0.1+50×0.2+70×0.4+90×0.3=68分.
20.(本小题满分12分)现有6道题,其中4道甲类题,2道乙类题,张同学从中任取2道题解答.试求:
(1)所取的2道题都是甲类题的概率;
(2)所取的2道题不是同一类题的概率.
[解析] (1)将4道甲类题依次编号为1,2,3,4;2道乙类题依次编号为5,6.任取2道题,基本事件为:{1,2},{1,3},{1,4},{1,5},{1,6},{2,3},{2,4},{2,5},{2,6},{3,4},{3,5},{3,6},{4,5},{4,6},{5,6},共15个,而且这些基本事件的出现是等可能的.
用A表示“都是甲类题”这一事件,则A包含的基本事件有{1,2},{1,3},{1,4},{2,3},{2,4},{3,4},共6个,所以P(A)==.
(2)基本事件同(1).用B表示“不是同一类题”这一事件,则B包含的基本事件有{1,5},{1,6},{2,5},{2,6},{3,5},{3,6},{4,5},{4,6},共8个,所以P(B)=.
21.(本小题满分12分)某高中在校学生2
000人,高一年级与高二年级人数相同并且都比高三年级多1人.为了响应市教育局“阳光体育”号召,该校开展了跑步和跳绳两项比赛,要求每人都参加而且只参加其中一项,各年级参与项目人数情况如下表:
年级项目
高一年级
高二年级
高三年级
跑步
a
b
c
跳绳
x
y
z
其中a∶b∶c=2∶3∶5,全校参与跳绳的人数占总人数的.为了了解学生对本次活动的满意度,采用分层抽样从中抽取一个200人的样本进行调查,则高二年级中参与跑步的同学应抽取多少人?
[解析] 全校参与跳绳的人数占总人数的,则跳绳的人数为×2
000=800,所以跑步的人数为×2
000=1
200.
又a∶b∶c=2∶3∶5,所以a=×1
200=240,b=×1
200=360,c=×1
200=600.
抽取样本为200人,即抽样比例为=,
则在抽取的样本中,应抽取的跑步的人数为×1
200=120,则跑步的抽取率为=,
所以高二年级中参与跑步的同学应抽取360×=36(人).
22.(本小题满分12分)砂糖橘是柑橘类的名优品种,因其味甜如砂糖故名.某果农选取一片山地种植砂糖橘,收获时,该果农随机选取果树20株作为样本测量它们每一株的果实产量(单位:kg),获得的所有数据按照区间[40,45],(45,50],(50,55],(55,60]进行分组,得到频率分布直方图如图.已知样本中产量在区间(45,50]上的果树株数是产量在区间(50,60]上的果树株数的倍.
(1)求a、b的值;
(2)从样本中产量在区间(50,60]上的果树里随机抽取两株,求产量在区间(55,60]上的果树至少有一株被抽中的概率.
[解析] (1)样本中产量在区间(45,50]上的果树有a×5×20=100a(株),
样本中产量在区间(50,60]上的果树有(b+0.02)×5×20=100(b+0.02)(株),
依题意,有100a=×100(b+0.02).即a=(b+0.02).①
根据频率分布直方图可知
(0.02+b+0.06+a)×5=1,②.
解①②组成的方程组得a=0.08,b=0.04.
(2)样本中产量在区间(50,55]上的果树有0.04×5×20=4(株),分别记为A1,A2,A3,A4,产量在区间(55,60]上的果树有0.02×5×20=2(株),分别记为B1,B2.
从这6株果树中随机抽取两株共有15种情况:(A1,A2),(A1,A3),(A1,A4),(A1,B1),(A1,B2),(A2,A3),(A2,A4),(A2,B1),(A2,B2),(A3,A4),(A3,B1),(A3,B2),(A4,B1),(A4,B2),(B1,B2).
其中产量在(55,60]上的果树至少有一株被抽中共有9种情况:(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(A4,B1),(A4,B2),(B1,B2).
记“从样本中产量在区间(50,60]上的果树里随机抽取两株,产量在区间(55,60]上的果树至少有一株被抽中”为事件M,则P(M)==.
(时间:120分钟 满分150分)
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.老师为研究男女同学数学学习的差异情况,对某班50名同学(其中男同学30名,女同学20名)采取分层抽样的方法,抽取一个容量为10的样本进行研究,则女同学甲被抽到的概率为( )
A.
B.
C.
D.
2.若某校高一年级8个班参加合唱比赛的得分如茎叶图所示,则这组数据的中位数和平均数分别是( )
A.91.5和91.5
B.91.5和92
C.91和91.5
D.92和92
3.学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n且支出在[20,60)元的样本,其频率分布直方图如图所示,根据此图估计学生在课外读物方面的支出费用的中位数为( )元( )
A.45
B.
C.
D.46
4.下列说法中,正确的是( )
A.数据5,4,4,3,5,2的众数是4
B.一组数据的标准差的平方是这组数据的方差
C.数据2,3,4,5的方差是数据4,6,8,10的方差的一半
D.频率分布直方图中各小矩形的面积等于相应各组的频数
5.从10个事件中任取一个事件,若这个事件是必然事件的概率为0.2,是不可能事件的概率为0.3,则这10个事件中随机事件的个数是( )
A.3
B.4
C.5
D.6
6.口袋内有一些大小相同的红球、黄球和白球,从中任意摸出一球,摸出的球是红球或黄球的概率为0.4,摸出的球是红球或白球的概率为0.9,那么摸出的球是黄球或白球的概率为( )
A.0.7
B.0.5
C.0.3
D.0.6
7.在5件产品中,有3件一等品和2件二等品,从中任取2件,以为概率的事件是( )
A.恰有2件一等品
B.至少有一件一等品
C.至多有一件一等品
D.都不是一等品
8.甲、乙两位同学各拿出6张游戏牌,用作投骰子的奖品,两人商定:骰子朝上的面的点数为奇数时甲得1分,否则乙得1分,先积得3分者获胜,得所有12张游戏牌,并结束游戏.比赛开始后,甲积2分,乙积1分,这时因意外事件中断游戏,以后他们不想再继续这场游戏,下面对这12张游戏牌的分配合理的是( )
A.甲得9张,乙得3张
B.甲得6张,乙得6张
C.甲得8张,乙得4张
D.甲得10张,乙得2张
二、多项选择题(本大题共4小题,每小题5分,共20分,在每小题给出的四个选项中,有多项是符合题目要求的.全部选对的得5分,选对但不全的得3分,有选错的得0分)
9.下列事件中,是随机事件的是( )
A.2021年8月18日,北京市不下雨
B.在标准大气压下,水在4
℃时结冰
C.从标有1,2,3,4的4张号签中任取一张,恰为1号签
D.若x∈R,则x2≥0
10.有甲、乙两种报纸供市民订阅,记事件E为“只订甲报纸”,事件F为“至少订一种报纸”,事件G为“至多订一种报纸”,事件H为“不订甲报纸”,事件I为“一种报纸也不订”.下列命题正确的是( )
A.E与G是互斥事件
B.F与I是互斥事件,且是对立事件
C.F与G不是互斥事件
D.G与I是互斥事件
11.某年级有12个班,现要从2班到12班中选1个班的学生参加一项活动,有人提议:掷两个骰子,得到的点数之和是几就选几班,这种做法( )
A.每个班被选到的概率都为
B.4班和10班被选到的概率都为
C.2班和12班被选到的概率最小
D.7班被选到的概率最大
12.在某地区某高传染性病毒流行期间,为了建立指标显示疫情已受控制,以便向该地区居民显示可以过正常生活,有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”,根据连续7天的新增病例数计算,下列各项中,一定符合上述指标的是( )
A.平均数≤3
B.标准差s≤2
C.平均数≤3且极差小于或等于2
D.众数等于1且极差小于或等于4
三、填空题(本大题共4小题,每小题5分,共20分,把答案填在题中的横线上)
13.某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮练习,每人投10次,投中的次数如下表:
学生
1号
2号
3号
4号
5号
甲班
6
7
7
8
7
乙班
6
7
6
7
9
则以上两组数据的方差中较小的一个为s2=___.
14.如图,从2014年参加南京青奥会知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如图所示.观察图形,估计这次奥运知识竞赛的及格率(大于或等于60分为及格)为____.
15.从字母a,b,c,d,e中任取两个不同字母,则取到字母a的概率为____.
16.某电子商务公司对10
000名网络购物者在2019年度的消费情况进行统计,发现消费金额(单位:万元)都在区间[0.3,0.9]内,其频率分布直方图如图所示.
(1)直方图中的a=____;
(2)在这些购物者中,消费金额在区间[0.5,0.9]内的购物者的人数为____.
四、解答题(本大题共6个小题,共70分,解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分10分)某人去开会,他乘火车、轮船、汽车、飞机去的概率分别为0.3,0.2,0.1,0.4.
(1)求他乘火车或乘飞机去的概率;
(2)若他去的概率为0.5,请问他有可能是乘何种交通工具去的?
18.(本小题满分12分)为了估计一次性木质筷子的用量,2017年从某市共600家高、中、低档饭店中抽取10家进行调查,得到这些饭店每天消耗的一次性筷子盒数分别为0.6,3.7,2.2,1.5,2.8,1.7,2.1,1.2,3.2,1.0.
(1)通过对样本的计算,估计该市2017年共消耗了多少盒一次性筷子.(每年按350个营业日计算)
(2)2019年又对该市一次性木筷的用量以同样的方式做了抽样调查,调查结果是10家饭店平均每家每天使用一次性筷子2.42盒,求该市2018年,2019年这两年一次性木质筷子用量平均每年增长的百分率.
(3)假如让你统计你所在省一年使用一次性木质筷子所消耗的木材量,如何利用统计知识去做?简单地说明你的做法.
19.(本小题满分12分)某班的全体学生共有50人,参加数学测试(百分制)成绩的频率分布直方图如图,数据的分组依次为:[20,40)、[40,60)、[60,80)、[80,100].依此表可以估计这一次测试成绩的中位数为70分.
(1)求表中a、b的值;
(2)请估计该班本次数学测试的平均分.
20.(本小题满分12分)现有6道题,其中4道甲类题,2道乙类题,张同学从中任取2道题解答.试求:
(1)所取的2道题都是甲类题的概率;
(2)所取的2道题不是同一类题的概率.
21.(本小题满分12分)某高中在校学生2
000人,高一年级与高二年级人数相同并且都比高三年级多1人.为了响应市教育局“阳光体育”号召,该校开展了跑步和跳绳两项比赛,要求每人都参加而且只参加其中一项,各年级参与项目人数情况如下表:
年级项目
高一年级
高二年级
高三年级
跑步
a
b
c
跳绳
x
y
z
其中a∶b∶c=2∶3∶5,全校参与跳绳的人数占总人数的.为了了解学生对本次活动的满意度,采用分层抽样从中抽取一个200人的样本进行调查,则高二年级中参与跑步的同学应抽取多少人?
22.(本小题满分12分)砂糖橘是柑橘类的名优品种,因其味甜如砂糖故名.某果农选取一片山地种植砂糖橘,收获时,该果农随机选取果树20株作为样本测量它们每一株的果实产量(单位:kg),获得的所有数据按照区间[40,45],(45,50],(50,55],(55,60]进行分组,得到频率分布直方图如图.已知样本中产量在区间(45,50]上的果树株数是产量在区间(50,60]上的果树株数的倍.
(1)求a、b的值;
(2)从样本中产量在区间(50,60]上的果树里随机抽取两株,求产量在区间(55,60]上的果树至少有一株被抽中的概率.
第五章综合测试
(时间:120分钟 满分150分)
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.老师为研究男女同学数学学习的差异情况,对某班50名同学(其中男同学30名,女同学20名)采取分层抽样的方法,抽取一个容量为10的样本进行研究,则女同学甲被抽到的概率为( C )
A.
B.
C.
D.
[解析] 因为在分层抽样中,任何个体被抽到的概率均相等,所以女同学甲被抽到的概率P==,故应选C.
2.若某校高一年级8个班参加合唱比赛的得分如茎叶图所示,则这组数据的中位数和平均数分别是( A )
A.91.5和91.5
B.91.5和92
C.91和91.5
D.92和92
[解析] 将这组数据从小到大排列,得87、89、90、91、92、93、94、96.
故平均数==91.5,中位数为=91.5,故选A.
3.学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n且支出在[20,60)元的样本,其频率分布直方图如图所示,根据此图估计学生在课外读物方面的支出费用的中位数为( )元( C )
A.45
B.
C.
D.46
[解析] 40+10×=.
4.下列说法中,正确的是( B )
A.数据5,4,4,3,5,2的众数是4
B.一组数据的标准差的平方是这组数据的方差
C.数据2,3,4,5的方差是数据4,6,8,10的方差的一半
D.频率分布直方图中各小矩形的面积等于相应各组的频数
[解析] A中的众数是4和5;C中,2,3,4,5的方差为1.25,而数据4,6,8,10的方差为5;D中,频率分布直方图中各小矩形的面积等于相应各组的频率.
5.从10个事件中任取一个事件,若这个事件是必然事件的概率为0.2,是不可能事件的概率为0.3,则这10个事件中随机事件的个数是( C )
A.3
B.4
C.5
D.6
[解析] 这10个事件中,必然事件的个数为10×0.2=2,不可能事件的个数为10×0.3=3.而必然事件、不可能事件、随机事件是彼此互斥的事件,且它们的个数和为10.故随机事件的个数为10-2-3=5.
6.口袋内有一些大小相同的红球、黄球和白球,从中任意摸出一球,摸出的球是红球或黄球的概率为0.4,摸出的球是红球或白球的概率为0.9,那么摸出的球是黄球或白球的概率为( A )
A.0.7
B.0.5
C.0.3
D.0.6
[解析] 任意摸出一球,事件A=“摸出红球”,事件B=“摸出黄球”,事件C=“摸出白球”,则A、B、C两两互斥.
由题设P(A∪B)=P(A)+P(B)=0.4,
P(A∪C)=P(A)+P(C)=0.9,
又P(A∪B∪C)=P(A)+P(B)+P(C)=1,
∴P(A)=0.4+0.9-1=0.3,
∴P(B∪C)=1-P(A)=1-0.3=0.7.
7.在5件产品中,有3件一等品和2件二等品,从中任取2件,以为概率的事件是( C )
A.恰有2件一等品
B.至少有一件一等品
C.至多有一件一等品
D.都不是一等品
[解析] 将3件一等品编号为1,2,3;2件二等品编号为4,5.从中任取2件有10种取法:(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5).其中恰含有1件一等品的取法有:(1,4),(1,5),(2,4),(2,5),(3,4),(3,5),恰有1件一等品的概率为P1=;恰有2件一等品的取法有:(1,2),(1,3),(2,3),故恰有2件一等品的概率为P2=,其对立事件是“至多有1件一等品”,概率为P3=1-P2=1-=.
8.甲、乙两位同学各拿出6张游戏牌,用作投骰子的奖品,两人商定:骰子朝上的面的点数为奇数时甲得1分,否则乙得1分,先积得3分者获胜,得所有12张游戏牌,并结束游戏.比赛开始后,甲积2分,乙积1分,这时因意外事件中断游戏,以后他们不想再继续这场游戏,下面对这12张游戏牌的分配合理的是( A )
A.甲得9张,乙得3张
B.甲得6张,乙得6张
C.甲得8张,乙得4张
D.甲得10张,乙得2张
[解析] 由题意,得骰子朝上的面的点数为奇数的概率为,即甲、乙每局得分的概率相等,
所以甲获胜的概率是+×=,
乙获胜的概率是×=.
所以甲得到的游戏牌为12×=9(张),乙得到的游戏牌为12×=3(张).
二、多项选择题(本大题共4小题,每小题5分,共20分,在每小题给出的四个选项中,有多项是符合题目要求的.全部选对的得5分,选对但不全的得3分,有选错的得0分)
9.下列事件中,是随机事件的是( AC )
A.2021年8月18日,北京市不下雨
B.在标准大气压下,水在4
℃时结冰
C.从标有1,2,3,4的4张号签中任取一张,恰为1号签
D.若x∈R,则x2≥0
[解析] AC为随机事件,B为不可能事件,D为必然事件.
10.有甲、乙两种报纸供市民订阅,记事件E为“只订甲报纸”,事件F为“至少订一种报纸”,事件G为“至多订一种报纸”,事件H为“不订甲报纸”,事件I为“一种报纸也不订”.下列命题正确的是( BC )
A.E与G是互斥事件
B.F与I是互斥事件,且是对立事件
C.F与G不是互斥事件
D.G与I是互斥事件
[解析] A.E与G不是互斥事件;B.F与I是互斥事件,且是对立事件;C.F与G不是互斥事件;D.G与I不是互斥事件.
11.某年级有12个班,现要从2班到12班中选1个班的学生参加一项活动,有人提议:掷两个骰子,得到的点数之和是几就选几班,这种做法( BCD )
A.每个班被选到的概率都为
B.4班和10班被选到的概率都为
C.2班和12班被选到的概率最小
D.7班被选到的概率最大
[解析] P(1)=0,P(2)=P(12)=,P(3)=P(11)=,P(4)=P(10)=,P(5)=P(9)=,P(6)=P(8)=,P(7)=,故选BCD.
12.在某地区某高传染性病毒流行期间,为了建立指标显示疫情已受控制,以便向该地区居民显示可以过正常生活,有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”,根据连续7天的新增病例数计算,下列各项中,一定符合上述指标的是( CD )
A.平均数≤3
B.标准差s≤2
C.平均数≤3且极差小于或等于2
D.众数等于1且极差小于或等于4
[解析] A中平均数≤3,可能是第一天0人,第二天6人,不符合题意;B中每天感染的人数均为10,标准差也是0,显然不符合题意;C符合,若极差等于0或1,在≤3的条件下,显然符合指标;若极差等于2且≤3,则每天新增感染人数的最小值与最大值有下列可能:(1)0,2,(2)1,3,(3)2,4,符合指标.D符合,若众数等于1且极差小于或等于4,则最大值不超过5,符合指标.
三、填空题(本大题共4小题,每小题5分,共20分,把答案填在题中的横线上)
13.某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮练习,每人投10次,投中的次数如下表:
学生
1号
2号
3号
4号
5号
甲班
6
7
7
8
7
乙班
6
7
6
7
9
则以上两组数据的方差中较小的一个为s2=____.
[解析] 甲=7,s=×(12+02+02+12+02)=;
乙=7,s=×(12+02+12+02+22)=.
∵s<s,∴方差中较小的一个为s,即s2=.
14.如图,从2014年参加南京青奥会知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如图所示.观察图形,估计这次奥运知识竞赛的及格率(大于或等于60分为及格)为__0.75__.
[解析] 及格率为1-(0.01+0.015)×10=0.75.
15.从字母a,b,c,d,e中任取两个不同字母,则取到字母a的概率为____.
[解析] 基本事件总数有10个,即(a,b),(a,c),(a,d),(a,e),(b,c),(b,d),(b,e),(c,d),(c,e),(d,e),其中含a的基本事件有(a,b),(a,c),(a,d),(a,e),共4个,故由古典概型知所求事件的概率P==.
16.某电子商务公司对10
000名网络购物者在2019年度的消费情况进行统计,发现消费金额(单位:万元)都在区间[0.3,0.9]内,其频率分布直方图如图所示.
(1)直方图中的a=__3__;
(2)在这些购物者中,消费金额在区间[0.5,0.9]内的购物者的人数为__6_000__.
[解析] (1)由频率分布直方图及频率和等于1可得0.2×0.1+0.8×0.1+1.5×0.1+2×0.1+2.5×0.1+a×0.1=1,解得a=3.
(2)消费金额在区间[0.5,0.9]内的频率为0.2×0.1+0.8×0.1+2×0.1+3×0.1=0.6,所以消费金额在区间[0.5,0.9]内的购物者的人数为0.6×10
000=6
000.
四、解答题(本大题共6个小题,共70分,解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分10分)某人去开会,他乘火车、轮船、汽车、飞机去的概率分别为0.3,0.2,0.1,0.4.
(1)求他乘火车或乘飞机去的概率;
(2)若他去的概率为0.5,请问他有可能是乘何种交通工具去的?
[解析] 设乘火车去开会为事件A,
乘轮船去开会为事件B,
乘汽车去开会为事件C,
乘飞机去开会为事件D,
则这四个事件是互斥事件.
(1)P(A+D)=P(A)+P(D)=0.3+0.4=0.7.
(2)∵0.5=0.2+0.3=0.1+0.4,
∴他可能乘的交通工具为①火车或轮船,②汽车或飞机.
18.(本小题满分12分)为了估计一次性木质筷子的用量,2017年从某市共600家高、中、低档饭店中抽取10家进行调查,得到这些饭店每天消耗的一次性筷子盒数分别为0.6,3.7,2.2,1.5,2.8,1.7,2.1,1.2,3.2,1.0.
(1)通过对样本的计算,估计该市2017年共消耗了多少盒一次性筷子.(每年按350个营业日计算)
(2)2019年又对该市一次性木筷的用量以同样的方式做了抽样调查,调查结果是10家饭店平均每家每天使用一次性筷子2.42盒,求该市2018年,2019年这两年一次性木质筷子用量平均每年增长的百分率.
(3)假如让你统计你所在省一年使用一次性木质筷子所消耗的木材量,如何利用统计知识去做?简单地说明你的做法.
[解析] (1)样本平均数为=(0.6+3.7+2.2+1.5+2.8+1.7+2.1+1.2+3.2+1.0)==2.
由样本平均数为2估计总体平均数也是2,故2017年该市600家饭店共消耗了一次性筷子为2×350×600=420
000(盒).
(2)由于2017一次性筷子用量是平均每天2盒,而2019年用量是平均每天2.42盒,设平均每年增长的百分率为x,依题意有2.42=2×(1+x)2,解得x=0.1=10%(x=-2.1舍去),所以该市2018年,2019年这两年一次性木质筷子的用量平均每年增长10%.
(3)先采用简单随机抽样的方法抽取若干县(市)(作样本),再从这些县(市)中采用分层抽样的方法抽取若干家饭店,统计一次性木质筷子用量的平均数,从而估计总体平均数,再进一步计算所消耗的木材总量.
19.(本小题满分12分)某班的全体学生共有50人,参加数学测试(百分制)成绩的频率分布直方图如图,数据的分组依次为:[20,40)、[40,60)、[60,80)、[80,100].依此表可以估计这一次测试成绩的中位数为70分.
(1)求表中a、b的值;
(2)请估计该班本次数学测试的平均分.
[解析] (1)由中位数为70可得,
0.005×20+0.01×20+a×10=0.5,
解得a=0.02.
又20(0.005+0.01+0.02+b)=1,
解得b=0.015.
(2)该班本次数学测试的平均分的估计值为30×0.1+50×0.2+70×0.4+90×0.3=68分.
20.(本小题满分12分)现有6道题,其中4道甲类题,2道乙类题,张同学从中任取2道题解答.试求:
(1)所取的2道题都是甲类题的概率;
(2)所取的2道题不是同一类题的概率.
[解析] (1)将4道甲类题依次编号为1,2,3,4;2道乙类题依次编号为5,6.任取2道题,基本事件为:{1,2},{1,3},{1,4},{1,5},{1,6},{2,3},{2,4},{2,5},{2,6},{3,4},{3,5},{3,6},{4,5},{4,6},{5,6},共15个,而且这些基本事件的出现是等可能的.
用A表示“都是甲类题”这一事件,则A包含的基本事件有{1,2},{1,3},{1,4},{2,3},{2,4},{3,4},共6个,所以P(A)==.
(2)基本事件同(1).用B表示“不是同一类题”这一事件,则B包含的基本事件有{1,5},{1,6},{2,5},{2,6},{3,5},{3,6},{4,5},{4,6},共8个,所以P(B)=.
21.(本小题满分12分)某高中在校学生2
000人,高一年级与高二年级人数相同并且都比高三年级多1人.为了响应市教育局“阳光体育”号召,该校开展了跑步和跳绳两项比赛,要求每人都参加而且只参加其中一项,各年级参与项目人数情况如下表:
年级项目
高一年级
高二年级
高三年级
跑步
a
b
c
跳绳
x
y
z
其中a∶b∶c=2∶3∶5,全校参与跳绳的人数占总人数的.为了了解学生对本次活动的满意度,采用分层抽样从中抽取一个200人的样本进行调查,则高二年级中参与跑步的同学应抽取多少人?
[解析] 全校参与跳绳的人数占总人数的,则跳绳的人数为×2
000=800,所以跑步的人数为×2
000=1
200.
又a∶b∶c=2∶3∶5,所以a=×1
200=240,b=×1
200=360,c=×1
200=600.
抽取样本为200人,即抽样比例为=,
则在抽取的样本中,应抽取的跑步的人数为×1
200=120,则跑步的抽取率为=,
所以高二年级中参与跑步的同学应抽取360×=36(人).
22.(本小题满分12分)砂糖橘是柑橘类的名优品种,因其味甜如砂糖故名.某果农选取一片山地种植砂糖橘,收获时,该果农随机选取果树20株作为样本测量它们每一株的果实产量(单位:kg),获得的所有数据按照区间[40,45],(45,50],(50,55],(55,60]进行分组,得到频率分布直方图如图.已知样本中产量在区间(45,50]上的果树株数是产量在区间(50,60]上的果树株数的倍.
(1)求a、b的值;
(2)从样本中产量在区间(50,60]上的果树里随机抽取两株,求产量在区间(55,60]上的果树至少有一株被抽中的概率.
[解析] (1)样本中产量在区间(45,50]上的果树有a×5×20=100a(株),
样本中产量在区间(50,60]上的果树有(b+0.02)×5×20=100(b+0.02)(株),
依题意,有100a=×100(b+0.02).即a=(b+0.02).①
根据频率分布直方图可知
(0.02+b+0.06+a)×5=1,②.
解①②组成的方程组得a=0.08,b=0.04.
(2)样本中产量在区间(50,55]上的果树有0.04×5×20=4(株),分别记为A1,A2,A3,A4,产量在区间(55,60]上的果树有0.02×5×20=2(株),分别记为B1,B2.
从这6株果树中随机抽取两株共有15种情况:(A1,A2),(A1,A3),(A1,A4),(A1,B1),(A1,B2),(A2,A3),(A2,A4),(A2,B1),(A2,B2),(A3,A4),(A3,B1),(A3,B2),(A4,B1),(A4,B2),(B1,B2).
其中产量在(55,60]上的果树至少有一株被抽中共有9种情况:(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(A4,B1),(A4,B2),(B1,B2).
记“从样本中产量在区间(50,60]上的果树里随机抽取两株,产量在区间(55,60]上的果树至少有一株被抽中”为事件M,则P(M)==.
