11.3.2直线与平面平行 同步练习2020-2021学年高一数学人教版B版(2019)必修第四册第十一章(Word含答解析案)
文档属性
| 名称 | 11.3.2直线与平面平行 同步练习2020-2021学年高一数学人教版B版(2019)必修第四册第十一章(Word含答解析案) |

|
|
| 格式 | docx | ||
| 文件大小 | 271.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-29 00:00:00 | ||
图片预览



文档简介
直线与平面平行
1.下列命题:
①如果一条直线不在平面内,则这条直线就与这个平面平行;
②过直线外一点,可以作无数个平面与这条直线平行;
③如果一条直线与平面平行,则它与平面内的任何直线平行.
其中正确命题的个数为
( )
A.0个
B.1个
C.2个
D.3个
2.如图,四棱锥P-ABCD中,M,N分别为AC,PC上的点,且MN∥平面PAD,则
( )
A.MN∥PD
B.MN∥PA
C.MN∥AD
D.以上均有可能
3.如图,在四面体ABCD中,若M,N,P分别为线段AB,BC,CD的中点,则直线BD与平面MNP的位置关系为
( )
A.平行
B.可能相交
C.相交或BD?平面MNP
D.以上都不对
4.以下命题(a,b表示直线,α表示平面):
①若a∥b,b?α,则a∥α;
②若a∥α,b∥α,则a∥b;
③若a∥b,b∥α,则a∥α;
④若a∥α,b?α,则a∥b.
其中正确命题的个数是 .?
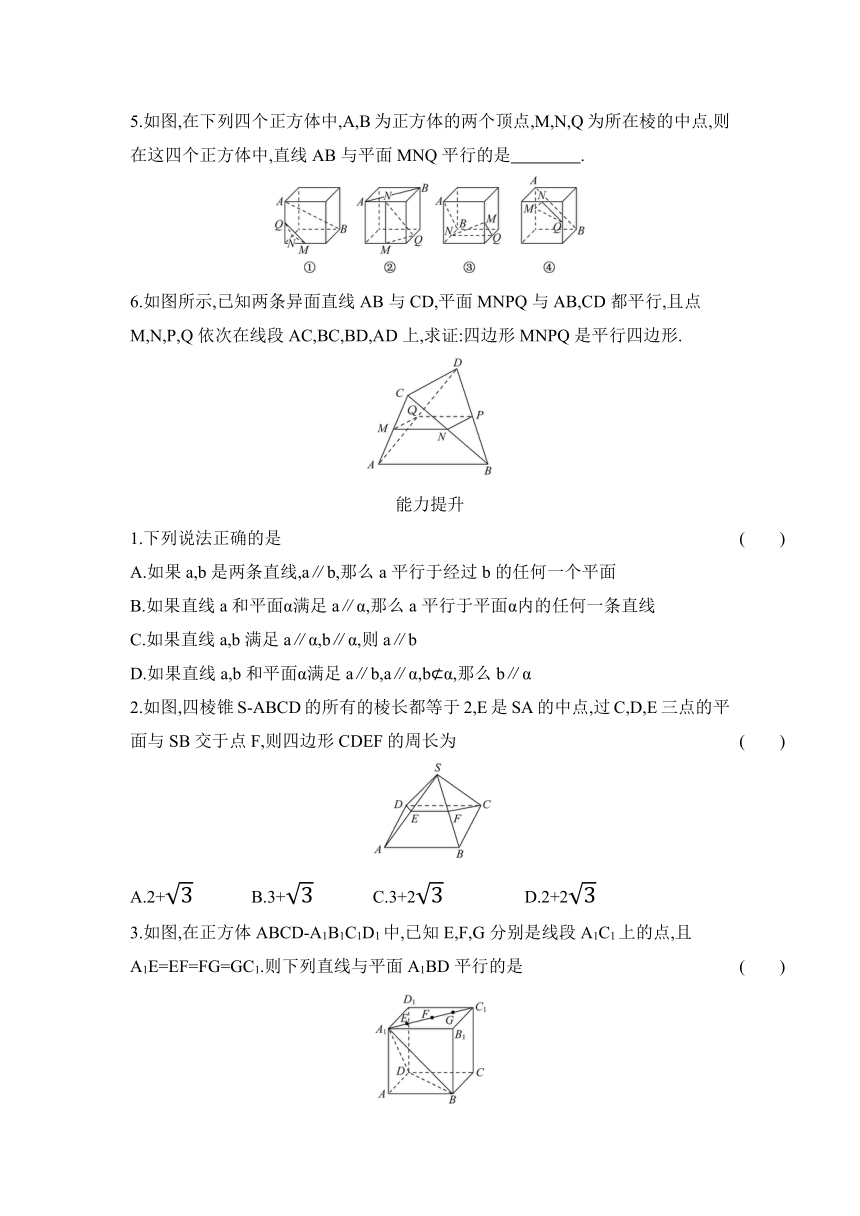
5.如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ平行的是 .?
6.如图所示,已知两条异面直线AB与CD,平面MNPQ与AB,CD都平行,且点M,N,P,Q依次在线段AC,BC,BD,AD上,求证:四边形MNPQ是平行四边形.
能力提升
1.下列说法正确的是
( )
A.如果a,b是两条直线,a∥b,那么a平行于经过b的任何一个平面
B.如果直线a和平面α满足a∥α,那么a平行于平面α内的任何一条直线
C.如果直线a,b满足a∥α,b∥α,则a∥b
D.如果直线a,b和平面α满足a∥b,a∥α,b?α,那么b∥α
2.如图,四棱锥S-ABCD的所有的棱长都等于2,E是SA的中点,过C,D,E三点的平面与SB交于点F,则四边形CDEF的周长为
( )
A.2+
B.3+
C.3+2
D.2+2
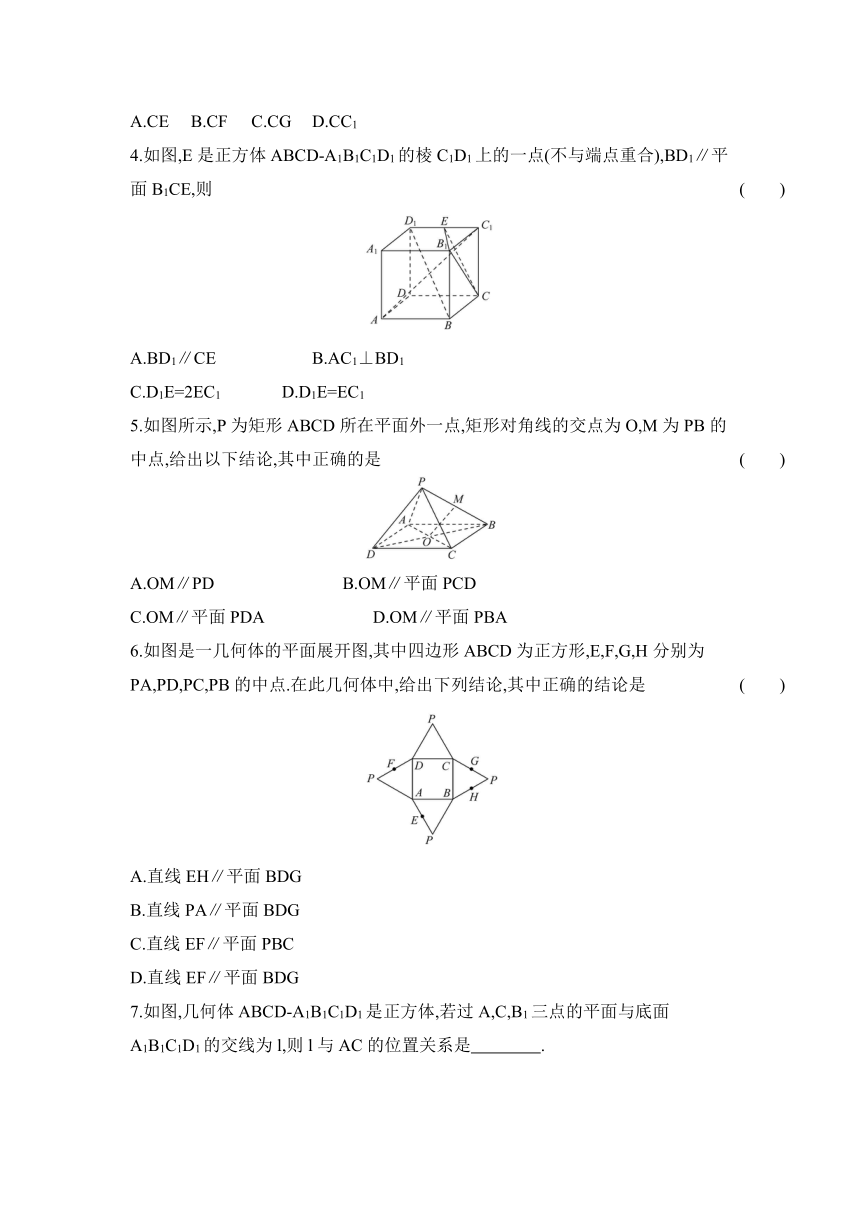
3.如图,在正方体ABCD-A1B1C1D1中,已知E,F,G分别是线段A1C1上的点,且A1E=EF=FG=GC1.则下列直线与平面A1BD平行的是
( )
A.CE
B.CF
C.CG
D.CC1
4.如图,E是正方体ABCD-A1B1C1D1的棱C1D1上的一点(不与端点重合),BD1∥平面B1CE,则
( )
A.BD1∥CE
B.AC1⊥BD1
C.D1E=2EC1
D.D1E=EC1
5.如图所示,P为矩形ABCD所在平面外一点,矩形对角线的交点为O,M为PB的中点,给出以下结论,其中正确的是
( )
A.OM∥PD
B.OM∥平面PCD
C.OM∥平面PDA
D.OM∥平面PBA
6.如图是一几何体的平面展开图,其中四边形ABCD为正方形,E,F,G,H分别为PA,PD,PC,PB的中点.在此几何体中,给出下列结论,其中正确的结论是
( )
A.直线EH∥平面BDG
B.直线PA∥平面BDG
C.直线EF∥平面PBC
D.直线EF∥平面BDG
7.如图,几何体ABCD-A1B1C1D1是正方体,若过A,C,B1三点的平面与底面A1B1C1D1的交线为l,则l与AC的位置关系是 .?
8.在正方体ABCD-A1B1C1D1中,E为棱CD上一点,且CE=2DE,F为棱AA1的中点,且平面BEF与DD1交于点G,与AC1交于点H,则= ,= .?
9.如图,在三棱柱ABC-A1B1C1中,D是棱CC1上的一点,P是AD的延长线与A1C1延长线的交点,且PB1∥平面BDA1,求证:CD=C1D.
10.如图,直三棱柱A1B1C1-ABC中,AC⊥BC,AC=BC=1,CC1=2,点M是A1B1的中点.
(1)求证:B1C∥平面AC1M;
(2)求三棱锥A1-AMC1的体积.
参考答案
1.下列命题:
①如果一条直线不在平面内,则这条直线就与这个平面平行;
②过直线外一点,可以作无数个平面与这条直线平行;
③如果一条直线与平面平行,则它与平面内的任何直线平行.
其中正确命题的个数为
( )
A.0个
B.1个
C.2个
D.3个
分析:选B.①直线与平面可以相交;②正确;③“任何直线”改为“无数条”才正确.
2.如图,四棱锥P-ABCD中,M,N分别为AC,PC上的点,且MN∥平面PAD,则
( )
A.MN∥PD
B.MN∥PA
C.MN∥AD
D.以上均有可能
分析:选B.四棱锥P-ABCD中,M,N分别为AC,PC上的点,且MN∥平面PAD,MN?平面PAC,平面PAC∩平面PAD=PA,MN?平面PAC,故由直线与平面平行的性质定理可得:MN∥PA.
3.如图,在四面体ABCD中,若M,N,P分别为线段AB,BC,CD的中点,则直线BD与平面MNP的位置关系为
( )
A.平行
B.可能相交
C.相交或BD?平面MNP
D.以上都不对
分析:选A.因为N,P分别为线段BC,CD的中点,所以NP∥BD,
又BD?平面MNP,NP?平面MNP,所以BD∥平面MNP.
4.以下命题(a,b表示直线,α表示平面):
①若a∥b,b?α,则a∥α;
②若a∥α,b∥α,则a∥b;
③若a∥b,b∥α,则a∥α;
④若a∥α,b?α,则a∥b.
其中正确命题的个数是 .?
分析:①要想a∥α,还需要a?α这个条件,故本命题是假命题;
②a,b除了平行以外还可以相交,异面,故本命题是假命题;
③还存在a?α这种可能性,故本命题是假命题;
④a,b可以是两条异面直线,故本命题是假命题,因此正确的命题的个数为零.
答案:0
5.如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ平行的是 .?
分析:要证明直线AB与平面MNQ平行,需要证明直线AB与平面MNQ内的一条直线平行,①平面MNQ中无法找到与直线AB平行的直线,所以①中直线AB与平面MNQ不平行;②由正方体性质可知MQ∥AB,又AB不在平面MNQ内,所以可以证得直线AB与平面MNQ平行;③由正方体性质可知MQ∥AB,又AB不在平面MNQ内,所以可以证得直线AB与平面MNQ平行;
④由正方体性质可知NQ∥AB,又AB不在平面MNQ内,所以可以证得直线AB与平面MNQ平行.
答案:②③④
6.如图所示,已知两条异面直线AB与CD,平面MNPQ与AB,CD都平行,且点M,N,P,Q依次在线段AC,BC,BD,AD上,求证:四边形MNPQ是平行四边形.
【证明】因为AB∥平面MNPQ,且过AB的平面ABC交平面MNPQ于MN,所以AB∥MN.
又过AB的平面ABD交平面MNPQ于PQ,所以AB∥PQ,所以MN∥PQ.同理可证NP∥MQ.
所以四边形MNPQ为平行四边形.
能力提升
1.下列说法正确的是
( )
A.如果a,b是两条直线,a∥b,那么a平行于经过b的任何一个平面
B.如果直线a和平面α满足a∥α,那么a平行于平面α内的任何一条直线
C.如果直线a,b满足a∥α,b∥α,则a∥b
D.如果直线a,b和平面α满足a∥b,a∥α,b?α,那么b∥α
分析:选D.如图,在长方体ABCD
-A′B′C′D′中,
AA′∥BB′,AA′却在过BB′的平面AB′内,
故选项A不正确;AA′∥平面B′C,BC?平面B′C,但AA′不平行于BC,故选项B不正确;AA′∥平面B′C,A′D′∥平面B′C,但AA′与A′D′相交,所以选项C不正确;选项D中,假设b与α相交,因为a∥b,所以a与α相交,这与a∥α矛盾,故b∥α,即选项D正确.
2.如图,四棱锥S-ABCD的所有的棱长都等于2,E是SA的中点,过C,D,E三点的平面与SB交于点F,则四边形CDEF的周长为
( )
A.2+
B.3+
C.3+2
D.2+2
分析:选C.因为CD∥AB,AB?平面SAB,CD?平面SAB,所以CD∥平面SAB.
又CD?平面CDEF,平面SAB∩平面CDEF=EF,
所以CD∥EF,且EF≠CD,因为E是SA的中点,EF∥AB,所以F是SB的中点,所以DE=CF,所以四边形CDEF为等腰梯形,
且CD=2,EF=1,DE=CF=,
所以四边形CDEF的周长为3+2.
3.如图,在正方体ABCD-A1B1C1D1中,已知E,F,G分别是线段A1C1上的点,且A1E=EF=FG=GC1.则下列直线与平面A1BD平行的是
( )
A.CE
B.CF
C.CG
D.CC1
分析:选B.如图,连接AC,使AC交BD于点O,连接A1O,CF,
则O为AC的中点,在正方体ABCD-A1B1C1D1中,AA1∥CC1且AA1=CC1,
则四边形AA1C1C为平行四边形,所以A1C1∥AC且A1C1=AC,
因为O,F分别为AC,A1C1的中点,所以A1F∥OC且A1F=OC,
所以四边形A1OCF为平行四边形,则CF∥A1O,
因为CF?平面A1BD,A1O?平面A1BD,
因此,CF∥平面A1BD.
4.如图,E是正方体ABCD-A1B1C1D1的棱C1D1上的一点(不与端点重合),BD1∥平面B1CE,则
( )
A.BD1∥CE
B.AC1⊥BD1
C.D1E=2EC1
D.D1E=EC1
分析:选D.如图,连接BC1,设B1C∩BC1=O,连接EO,可得平面D1BC1∩平面B1CE=EO,因为BD1∥平面B1CE,根据线面平行的性质可得BD1∥EO,因为O为BC1的中点,所以E为C1D1的中点,所以D1E=EC1.
5.如图所示,P为矩形ABCD所在平面外一点,矩形对角线的交点为O,M为PB的中点,给出以下结论,其中正确的是
( )
A.OM∥PD
B.OM∥平面PCD
C.OM∥平面PDA
D.OM∥平面PBA
分析:选ABC.由题意知,OM是△BPD的中位线,
所以OM∥PD,故A正确;PD?平面PCD,OM?平面PCD,
所以OM∥平面PCD,故B正确;同理,可得OM∥平面PDA,故C正确;
OM与平面PBA相交,故D不正确.
6.如图是一几何体的平面展开图,其中四边形ABCD为正方形,E,F,G,H分别为PA,PD,PC,PB的中点.在此几何体中,给出下列结论,其中正确的结论是
( )
A.直线EH∥平面BDG
B.直线PA∥平面BDG
C.直线EF∥平面PBC
D.直线EF∥平面BDG
分析:选BC.作出立体图形如图所示.连接DG,BG,EF,FG,GH,EH,AC,BD且AC∩BD=M,连接GM.
对于A,因为E,H分别是PA,PB的中点,所以EH∥AB.
再结合图形可得,AB∩BD=B,则直线EH与平面BDG不平行,故A错误;
对于B,由题意知M为AC与BD的中点,所以MG∥PA,
又MG?平面BDG,PA?平面BDG,所以PA∥平面BDG,故B正确;
对于C,由题意知EF∥AD,AD∥BC,所以EF∥BC,
因为EF?平面PBC,BC?平面PBC,所以直线EF∥平面PBC,故C正确;
对于D,根据C中的分析可知EF∥BC,再结合图形可得,BC∩BD=B,则直线EF与平面BDG不平行,故D错误.
7.如图,几何体ABCD-A1B1C1D1是正方体,若过A,C,B1三点的平面与底面A1B1C1D1的交线为l,则l与AC的位置关系是 .?
分析:连接A1C1,
因为AC∥A1C1,A1C1?平面A1B1C1D1,AC?平面A1B1C1D1,
所以AC∥平面A1B1C1D1,
又AC?平面AB1C,平面AB1C∩平面A1B1C1D1=l,所以AC∥l.
答案:AC∥l
8.在正方体ABCD-A1B1C1D1中,E为棱CD上一点,且CE=2DE,F为棱AA1的中点,且平面BEF与DD1交于点G,与AC1交于点H,则= ,= .?
分析:因为ABCD-A1B1C1D1是正方体,
所以平面A1B1BA∥平面C1D1DC,
因为BF?平面A1B1BA,所以BF∥平面CDD1C1,
因为平面BFGE∩平面C1D1DC=GE,
则BF∥GE,则=,即=,
又CE=2DE,则=.
连接AC交BE于M,过M作MN∥CC1,MN与AC1交于N,连接FM,则H为FM与AC1的交点.
因为AB∥CE,所以==,则==.
所以=,所以==,故=.
答案:
9.如图,在三棱柱ABC-A1B1C1中,D是棱CC1上的一点,P是AD的延长线与A1C1延长线的交点,且PB1∥平面BDA1,求证:CD=C1D.
【证明】如图,连接AB1与BA1交于点O,连接OD,
因为PB1∥平面BDA1,PB1?平面AB1P,
平面AB1P∩平面BDA1=OD,所以OD∥PB1,
又AO=B1O,所以AD=PD,
又AC∥C1P,所以CD=C1D.
10.如图,直三棱柱A1B1C1-ABC中,AC⊥BC,AC=BC=1,CC1=2,点M是A1B1的中点.
(1)求证:B1C∥平面AC1M;
(2)求三棱锥A1-AMC1的体积.
分析:(1)连接A1C交AC1于N,则N为A1C的中点,
又因为M为A1B1的中点,所以MN∥B1C,
又因为MN?平面AC1M,B1C?平面AC1M,
所以B1C∥平面AC1M.
(2)因为直三棱柱A1B1C1-ABC中,AC⊥BC,AC=BC=1,CC1=2,且点M是A1B1的中点,
所以=
=×AA1=××AA1
=×××1×1×2=.
1.下列命题:
①如果一条直线不在平面内,则这条直线就与这个平面平行;
②过直线外一点,可以作无数个平面与这条直线平行;
③如果一条直线与平面平行,则它与平面内的任何直线平行.
其中正确命题的个数为
( )
A.0个
B.1个
C.2个
D.3个
2.如图,四棱锥P-ABCD中,M,N分别为AC,PC上的点,且MN∥平面PAD,则
( )
A.MN∥PD
B.MN∥PA
C.MN∥AD
D.以上均有可能
3.如图,在四面体ABCD中,若M,N,P分别为线段AB,BC,CD的中点,则直线BD与平面MNP的位置关系为
( )
A.平行
B.可能相交
C.相交或BD?平面MNP
D.以上都不对
4.以下命题(a,b表示直线,α表示平面):
①若a∥b,b?α,则a∥α;
②若a∥α,b∥α,则a∥b;
③若a∥b,b∥α,则a∥α;
④若a∥α,b?α,则a∥b.
其中正确命题的个数是 .?
5.如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ平行的是 .?
6.如图所示,已知两条异面直线AB与CD,平面MNPQ与AB,CD都平行,且点M,N,P,Q依次在线段AC,BC,BD,AD上,求证:四边形MNPQ是平行四边形.
能力提升
1.下列说法正确的是
( )
A.如果a,b是两条直线,a∥b,那么a平行于经过b的任何一个平面
B.如果直线a和平面α满足a∥α,那么a平行于平面α内的任何一条直线
C.如果直线a,b满足a∥α,b∥α,则a∥b
D.如果直线a,b和平面α满足a∥b,a∥α,b?α,那么b∥α
2.如图,四棱锥S-ABCD的所有的棱长都等于2,E是SA的中点,过C,D,E三点的平面与SB交于点F,则四边形CDEF的周长为
( )
A.2+
B.3+
C.3+2
D.2+2
3.如图,在正方体ABCD-A1B1C1D1中,已知E,F,G分别是线段A1C1上的点,且A1E=EF=FG=GC1.则下列直线与平面A1BD平行的是
( )
A.CE
B.CF
C.CG
D.CC1
4.如图,E是正方体ABCD-A1B1C1D1的棱C1D1上的一点(不与端点重合),BD1∥平面B1CE,则
( )
A.BD1∥CE
B.AC1⊥BD1
C.D1E=2EC1
D.D1E=EC1
5.如图所示,P为矩形ABCD所在平面外一点,矩形对角线的交点为O,M为PB的中点,给出以下结论,其中正确的是
( )
A.OM∥PD
B.OM∥平面PCD
C.OM∥平面PDA
D.OM∥平面PBA
6.如图是一几何体的平面展开图,其中四边形ABCD为正方形,E,F,G,H分别为PA,PD,PC,PB的中点.在此几何体中,给出下列结论,其中正确的结论是
( )
A.直线EH∥平面BDG
B.直线PA∥平面BDG
C.直线EF∥平面PBC
D.直线EF∥平面BDG
7.如图,几何体ABCD-A1B1C1D1是正方体,若过A,C,B1三点的平面与底面A1B1C1D1的交线为l,则l与AC的位置关系是 .?
8.在正方体ABCD-A1B1C1D1中,E为棱CD上一点,且CE=2DE,F为棱AA1的中点,且平面BEF与DD1交于点G,与AC1交于点H,则= ,= .?
9.如图,在三棱柱ABC-A1B1C1中,D是棱CC1上的一点,P是AD的延长线与A1C1延长线的交点,且PB1∥平面BDA1,求证:CD=C1D.
10.如图,直三棱柱A1B1C1-ABC中,AC⊥BC,AC=BC=1,CC1=2,点M是A1B1的中点.
(1)求证:B1C∥平面AC1M;
(2)求三棱锥A1-AMC1的体积.
参考答案
1.下列命题:
①如果一条直线不在平面内,则这条直线就与这个平面平行;
②过直线外一点,可以作无数个平面与这条直线平行;
③如果一条直线与平面平行,则它与平面内的任何直线平行.
其中正确命题的个数为
( )
A.0个
B.1个
C.2个
D.3个
分析:选B.①直线与平面可以相交;②正确;③“任何直线”改为“无数条”才正确.
2.如图,四棱锥P-ABCD中,M,N分别为AC,PC上的点,且MN∥平面PAD,则
( )
A.MN∥PD
B.MN∥PA
C.MN∥AD
D.以上均有可能
分析:选B.四棱锥P-ABCD中,M,N分别为AC,PC上的点,且MN∥平面PAD,MN?平面PAC,平面PAC∩平面PAD=PA,MN?平面PAC,故由直线与平面平行的性质定理可得:MN∥PA.
3.如图,在四面体ABCD中,若M,N,P分别为线段AB,BC,CD的中点,则直线BD与平面MNP的位置关系为
( )
A.平行
B.可能相交
C.相交或BD?平面MNP
D.以上都不对
分析:选A.因为N,P分别为线段BC,CD的中点,所以NP∥BD,
又BD?平面MNP,NP?平面MNP,所以BD∥平面MNP.
4.以下命题(a,b表示直线,α表示平面):
①若a∥b,b?α,则a∥α;
②若a∥α,b∥α,则a∥b;
③若a∥b,b∥α,则a∥α;
④若a∥α,b?α,则a∥b.
其中正确命题的个数是 .?
分析:①要想a∥α,还需要a?α这个条件,故本命题是假命题;
②a,b除了平行以外还可以相交,异面,故本命题是假命题;
③还存在a?α这种可能性,故本命题是假命题;
④a,b可以是两条异面直线,故本命题是假命题,因此正确的命题的个数为零.
答案:0
5.如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ平行的是 .?
分析:要证明直线AB与平面MNQ平行,需要证明直线AB与平面MNQ内的一条直线平行,①平面MNQ中无法找到与直线AB平行的直线,所以①中直线AB与平面MNQ不平行;②由正方体性质可知MQ∥AB,又AB不在平面MNQ内,所以可以证得直线AB与平面MNQ平行;③由正方体性质可知MQ∥AB,又AB不在平面MNQ内,所以可以证得直线AB与平面MNQ平行;
④由正方体性质可知NQ∥AB,又AB不在平面MNQ内,所以可以证得直线AB与平面MNQ平行.
答案:②③④
6.如图所示,已知两条异面直线AB与CD,平面MNPQ与AB,CD都平行,且点M,N,P,Q依次在线段AC,BC,BD,AD上,求证:四边形MNPQ是平行四边形.
【证明】因为AB∥平面MNPQ,且过AB的平面ABC交平面MNPQ于MN,所以AB∥MN.
又过AB的平面ABD交平面MNPQ于PQ,所以AB∥PQ,所以MN∥PQ.同理可证NP∥MQ.
所以四边形MNPQ为平行四边形.
能力提升
1.下列说法正确的是
( )
A.如果a,b是两条直线,a∥b,那么a平行于经过b的任何一个平面
B.如果直线a和平面α满足a∥α,那么a平行于平面α内的任何一条直线
C.如果直线a,b满足a∥α,b∥α,则a∥b
D.如果直线a,b和平面α满足a∥b,a∥α,b?α,那么b∥α
分析:选D.如图,在长方体ABCD
-A′B′C′D′中,
AA′∥BB′,AA′却在过BB′的平面AB′内,
故选项A不正确;AA′∥平面B′C,BC?平面B′C,但AA′不平行于BC,故选项B不正确;AA′∥平面B′C,A′D′∥平面B′C,但AA′与A′D′相交,所以选项C不正确;选项D中,假设b与α相交,因为a∥b,所以a与α相交,这与a∥α矛盾,故b∥α,即选项D正确.
2.如图,四棱锥S-ABCD的所有的棱长都等于2,E是SA的中点,过C,D,E三点的平面与SB交于点F,则四边形CDEF的周长为
( )
A.2+
B.3+
C.3+2
D.2+2
分析:选C.因为CD∥AB,AB?平面SAB,CD?平面SAB,所以CD∥平面SAB.
又CD?平面CDEF,平面SAB∩平面CDEF=EF,
所以CD∥EF,且EF≠CD,因为E是SA的中点,EF∥AB,所以F是SB的中点,所以DE=CF,所以四边形CDEF为等腰梯形,
且CD=2,EF=1,DE=CF=,
所以四边形CDEF的周长为3+2.
3.如图,在正方体ABCD-A1B1C1D1中,已知E,F,G分别是线段A1C1上的点,且A1E=EF=FG=GC1.则下列直线与平面A1BD平行的是
( )
A.CE
B.CF
C.CG
D.CC1
分析:选B.如图,连接AC,使AC交BD于点O,连接A1O,CF,
则O为AC的中点,在正方体ABCD-A1B1C1D1中,AA1∥CC1且AA1=CC1,
则四边形AA1C1C为平行四边形,所以A1C1∥AC且A1C1=AC,
因为O,F分别为AC,A1C1的中点,所以A1F∥OC且A1F=OC,
所以四边形A1OCF为平行四边形,则CF∥A1O,
因为CF?平面A1BD,A1O?平面A1BD,
因此,CF∥平面A1BD.
4.如图,E是正方体ABCD-A1B1C1D1的棱C1D1上的一点(不与端点重合),BD1∥平面B1CE,则
( )
A.BD1∥CE
B.AC1⊥BD1
C.D1E=2EC1
D.D1E=EC1
分析:选D.如图,连接BC1,设B1C∩BC1=O,连接EO,可得平面D1BC1∩平面B1CE=EO,因为BD1∥平面B1CE,根据线面平行的性质可得BD1∥EO,因为O为BC1的中点,所以E为C1D1的中点,所以D1E=EC1.
5.如图所示,P为矩形ABCD所在平面外一点,矩形对角线的交点为O,M为PB的中点,给出以下结论,其中正确的是
( )
A.OM∥PD
B.OM∥平面PCD
C.OM∥平面PDA
D.OM∥平面PBA
分析:选ABC.由题意知,OM是△BPD的中位线,
所以OM∥PD,故A正确;PD?平面PCD,OM?平面PCD,
所以OM∥平面PCD,故B正确;同理,可得OM∥平面PDA,故C正确;
OM与平面PBA相交,故D不正确.
6.如图是一几何体的平面展开图,其中四边形ABCD为正方形,E,F,G,H分别为PA,PD,PC,PB的中点.在此几何体中,给出下列结论,其中正确的结论是
( )
A.直线EH∥平面BDG
B.直线PA∥平面BDG
C.直线EF∥平面PBC
D.直线EF∥平面BDG
分析:选BC.作出立体图形如图所示.连接DG,BG,EF,FG,GH,EH,AC,BD且AC∩BD=M,连接GM.
对于A,因为E,H分别是PA,PB的中点,所以EH∥AB.
再结合图形可得,AB∩BD=B,则直线EH与平面BDG不平行,故A错误;
对于B,由题意知M为AC与BD的中点,所以MG∥PA,
又MG?平面BDG,PA?平面BDG,所以PA∥平面BDG,故B正确;
对于C,由题意知EF∥AD,AD∥BC,所以EF∥BC,
因为EF?平面PBC,BC?平面PBC,所以直线EF∥平面PBC,故C正确;
对于D,根据C中的分析可知EF∥BC,再结合图形可得,BC∩BD=B,则直线EF与平面BDG不平行,故D错误.
7.如图,几何体ABCD-A1B1C1D1是正方体,若过A,C,B1三点的平面与底面A1B1C1D1的交线为l,则l与AC的位置关系是 .?
分析:连接A1C1,
因为AC∥A1C1,A1C1?平面A1B1C1D1,AC?平面A1B1C1D1,
所以AC∥平面A1B1C1D1,
又AC?平面AB1C,平面AB1C∩平面A1B1C1D1=l,所以AC∥l.
答案:AC∥l
8.在正方体ABCD-A1B1C1D1中,E为棱CD上一点,且CE=2DE,F为棱AA1的中点,且平面BEF与DD1交于点G,与AC1交于点H,则= ,= .?
分析:因为ABCD-A1B1C1D1是正方体,
所以平面A1B1BA∥平面C1D1DC,
因为BF?平面A1B1BA,所以BF∥平面CDD1C1,
因为平面BFGE∩平面C1D1DC=GE,
则BF∥GE,则=,即=,
又CE=2DE,则=.
连接AC交BE于M,过M作MN∥CC1,MN与AC1交于N,连接FM,则H为FM与AC1的交点.
因为AB∥CE,所以==,则==.
所以=,所以==,故=.
答案:
9.如图,在三棱柱ABC-A1B1C1中,D是棱CC1上的一点,P是AD的延长线与A1C1延长线的交点,且PB1∥平面BDA1,求证:CD=C1D.
【证明】如图,连接AB1与BA1交于点O,连接OD,
因为PB1∥平面BDA1,PB1?平面AB1P,
平面AB1P∩平面BDA1=OD,所以OD∥PB1,
又AO=B1O,所以AD=PD,
又AC∥C1P,所以CD=C1D.
10.如图,直三棱柱A1B1C1-ABC中,AC⊥BC,AC=BC=1,CC1=2,点M是A1B1的中点.
(1)求证:B1C∥平面AC1M;
(2)求三棱锥A1-AMC1的体积.
分析:(1)连接A1C交AC1于N,则N为A1C的中点,
又因为M为A1B1的中点,所以MN∥B1C,
又因为MN?平面AC1M,B1C?平面AC1M,
所以B1C∥平面AC1M.
(2)因为直三棱柱A1B1C1-ABC中,AC⊥BC,AC=BC=1,CC1=2,且点M是A1B1的中点,
所以=
=×AA1=××AA1
=×××1×1×2=.
