第十一章 三角形 复习小结 课件(共35张PPT)
文档属性
| 名称 | 第十一章 三角形 复习小结 课件(共35张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-29 00:00:00 | ||
图片预览







文档简介
(共35张PPT)
人教版
八年级上
三角形复习小结
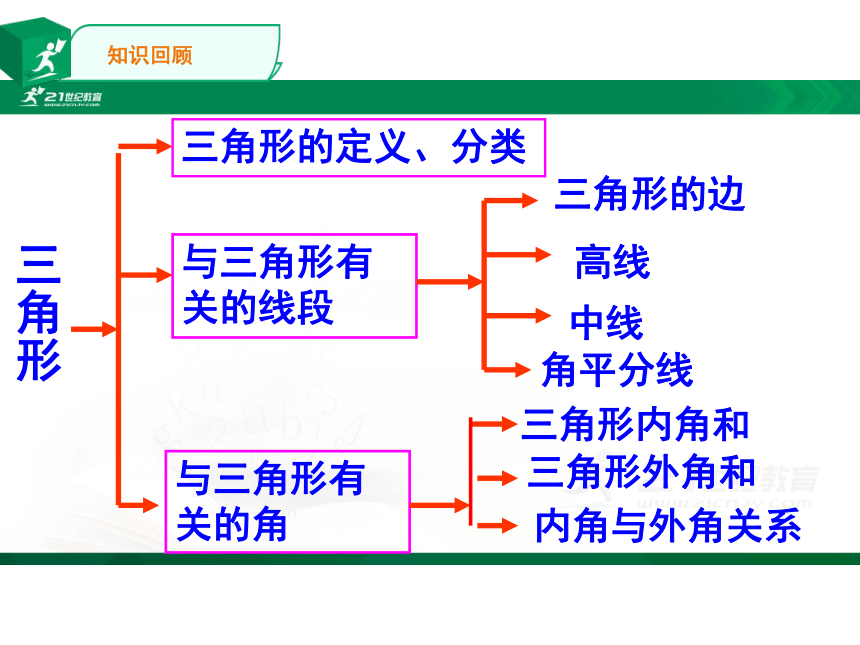
三角形
与三角形有关的线段
三角形内角和
三角形外角和
三角形的边
高线
中线
角平分线
与三角形有关的角
内角与外角关系
三角形的定义、分类
知识回顾
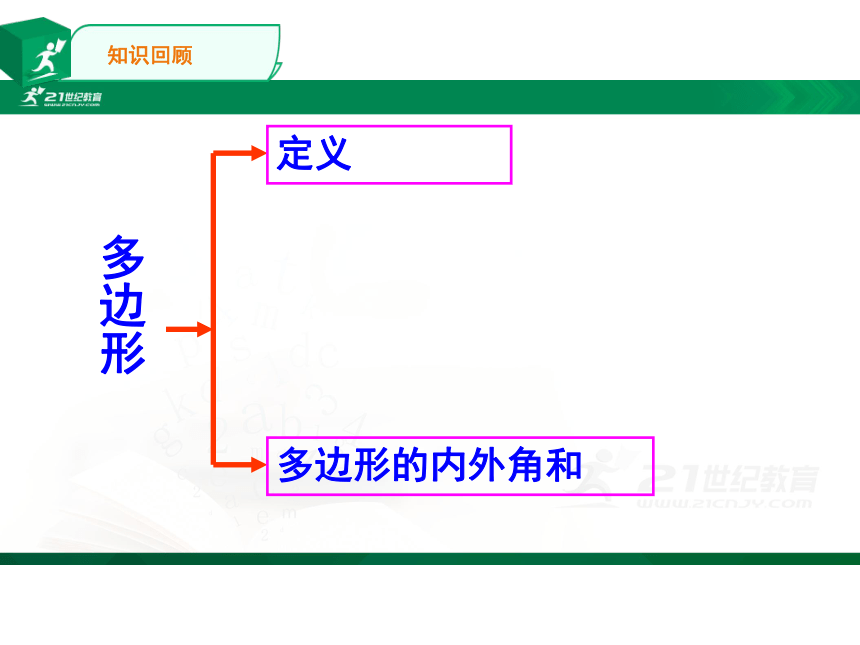
多边形
定义
多边形的内外角和
知识回顾
A
C
B
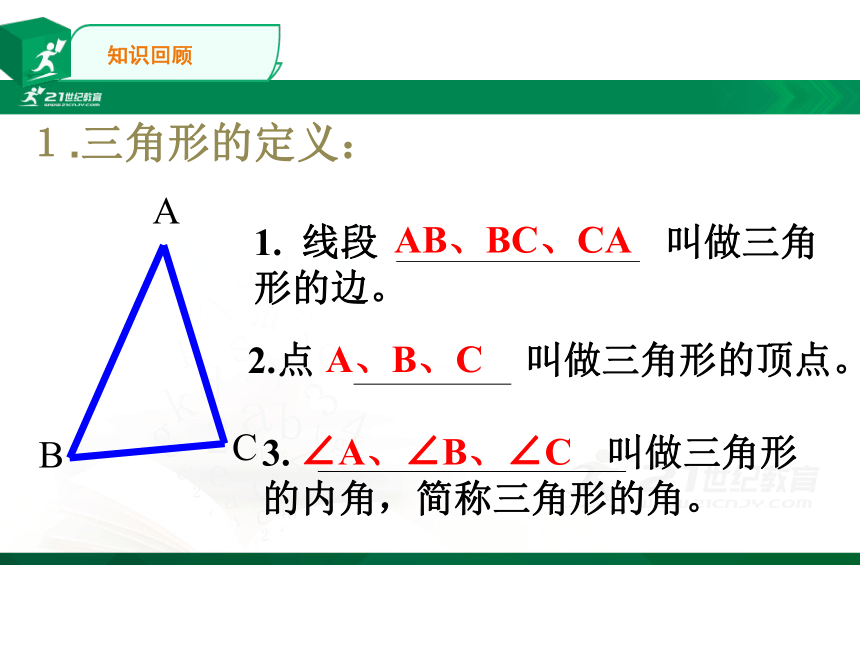
1.
线段
叫做三角形的边。
2.点
叫做三角形的顶点。
3.
叫做三角形的内角,简称三角形的角。
1.三角形的定义:
AB、BC、CA
A、B、C
∠A、∠B、∠C
知识回顾
A
C
B
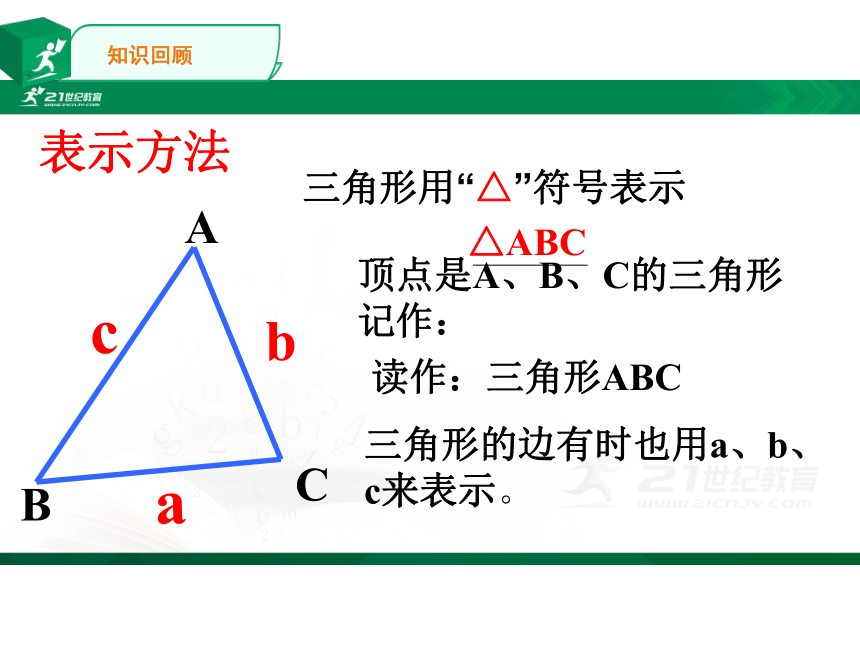
顶点是A、B、C的三角形记作:
a
c
b
读作:三角形ABC
三角形的边有时也用a、b、c来表示。
三角形用“△”符号表示
表示方法
△ABC
知识回顾
1.图中有几个三角形?用符号表示这些三角形。
2.以AB为边的三角形有哪些?
△ABC、△ABE
3.以E为顶点的三角形有哪些?
△ABE、△BCE、△CDE
5个:ΔABE、ΔBEC、
ΔECD、ΔABC、ΔBCD
A
B
E
C
D
小试牛刀
2.三角形的分类
锐角三角形
三角形
钝角三角形
(1)按角分
直角三角形
斜三角形
(2)按边分
腰和底不等的等腰三角形
三角形
等腰三角形
等边三角形
不等边三角形
知识回顾
1.三角形的三边关系:
(1)三角形两边的和大于第三边;
2.判断三条已知线段a、b、c能否
组成三角形。
当a最长,且有b+c>a时,就可构成三角形。
3.确定三角形第三边的取值范围:
两边之差<第三边<两边之和。
(2)三角形两边的差小于第三边。
知识回顾
三角形一个角的平分线与它的对边相交,这个角
的
之间的线段叫做三角形的角平分线。
连结三角形一个
的线段叫做三角形的中线。
从三角形的一个顶点向它的对边所在直线作垂线,_______________
的线段叫做三角形的高线。
1.三角形的高线定义:
顶点和垂足之间
2.三角形角平分线的定义:
顶点与交点
3.三角形的中线定义:
顶点与它对边中点
知识回顾
4.三角形的三条高线(或高线所在直线)交于一点(垂心)。
锐角三角形三条高线交于三角形内部一点,
直角三角形三条高线交于直角顶点,
钝角三角形三条高线所在直线交于三角形
外部一点。
5.三角形的三条中线交于三角形内部一点(重心)。
6.三角形的三条角平分线交于三角形内部一点(内心)。
知识回顾
1.三角形内角和定理
三角形的内角和等于180°,
直角三角形的两个锐角互余。
2.三角形外角和定理
三角形的外角和等于360°。
三角形的一个外角等于与它不相邻的两个内角的和。
3.三角形的外角与内角的关系
三角形的一个外角大于与它不相邻的任何一个内角。
知识回顾
三角形木架的形状不会改变,而四边形木架的形状会改变。
这就是说,三角形具有稳定性,而四边形没有稳定性。
知识回顾
三角形
长方形
六边形
四边形
八边形
在平面内,由一些不在同一条直线上的线段首尾顺次相接组成的图形叫做多边形。
你能仿照三角形的定义给出多边形的定义吗?
知识回顾
内角
对角线
对角线:连接多边形不相邻的两个顶点的线段。
可表示为:五边形ABCDE或五边形AEDCB
A
B
C
D
E
外角
1
知识回顾
请分别画出下列两个图形各边所在的直线,你能得到什么结论?
(1)
(2)
如图(1)这样,画出多边形的任何一条边所在的直线,整个多边形都在这条直线的同一侧,那么这个多边形就是凸多边形。本节我们只讨论凸多边形。
A
B
C
D
E
F
G
H
知识回顾
观察下面每个多边形的边、角有何特点?
在平面内,各个角都相等,各条边也都相等的多边形叫做正多边形。
知识回顾
n边形的内角和等于(n-2)·180°。
多边形的外角和都等于360°。
知识回顾
我们通过把多边形划分为若干个三角形,用三角形内角和去求多边形内角和,从而得到多边形的内角和公式为(n-2)×180°。这种化未知为已知的转化方法,必须在学习中逐渐掌握。由于多边形外角和为360°,与边数无关,所以常把多边形内角和的问题转化为外角和来处理。
知识回顾
1.在△ABC中,
(1)∠B=100°,∠A=∠C,则∠C=
;
(2)2∠A=∠B+∠C,∠A=
。
2.如图,______是△ACD的外角,
∠ADB=115°,∠CAD=80°则∠C=___。
40°
60°
35°
A
B
C
D
∠ADB
巩固练习
3.下列条件中能组成三角形的是(
)
A.5cm,13cm,7cm
B.3cm,5cm,9cm
C.14cm,9cm,6cm
D.5cm,6cm,11cm
C
4.三角形的两边为7cm和5cm,则第三边x的
范围是_____________。
2cm<x<12cm
巩固练习
5.如右图,AD是BC边上的高,BE是△ABD的角平分线,∠1=40°,∠2=30°,
则∠C=____,∠BED=_____
。
65°
60°
6.直角三角形的两个锐角相等,则每一个锐角等于_____度。
A
B
C
D
1
2
E
45
巩固练习
7.在△ABC中,∠A是∠B的2倍,∠C比∠A+∠B还大30°,则∠C的外角为_____度,这个三角形是____三角形。
75
钝角
8.如图,已知:AD是△ABC的中线,△ABC的面积为50cm2,则△ABD的面积是_______。
25cm2
A
B
C
D
巩固练习
解:由三角形两边之和大于第三边,
两边之差小于第三边得:
8-3又∵第三边长为奇数,
∴第三条边长为7cm、9cm。
1.已知两条线段的长分别是3cm、8cm,要想拼成一个三角形,且第三条线段a的长为奇数,问第三条线段应取多少长?
拓展训练
2.有一等腰三角形,一边的长是5cm,另一边的长是8cm,求它的周长。
解:(1)当腰长为5cm时,它的周长为:
5+5+8=18(cm)
(2)当腰长为8cm时,它的周长为:
8+8+5=21(cm)
∴这个三角形的周长为18cm或21cm。
拓展训练
1
D
C
A
B
3.已知∠B=42°,∠A+10°=∠1,∠ACD=64°,说明AB//CD。
拓展训练
A
B
C
X
1
2
3
4
4.已知∠1=∠2,∠3=∠4,∠A=100°,求X的值。
拓展训练
5.如图,△ABC中,∠A=∠ABD,∠C=∠BDC=∠ABC,求∠DBC的度数。
A
B
C
D
拓展训练
友情提示:
把图形内部七边形各角看作外部三角形外角,分析可得
6.求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数。
A
G
F
E
D
C
B
7×180°-2×360°=540°
拓展训练
1.三角形三个内角的度数分别是(x+y)°,(x-y)°,x°,且x>y>0,则该三角形有一个内角为( )
A.30°
B.45°
C.60°
D.90°
2.把14cm长的细铁丝截成三段,围成不是等边三角形的三角形,并且使三边长均为整数,那么( )
A.只有一种截法
B.只有两种截法
C.有三种截法
D.有四种截法
3.等腰三角形的腰长为a,底为X,则X的取值范围是( )
A.0<X<2a
B.0<X<a
C.0<X≤a
D.0<X≤2a
C
D
A
当堂评价
4.一个正多边形每一个内角都是120°,这个多边形是( )
A.正四边形
B.正五边形
C.正六边形
D.正七边形
5.一个多边形木板,截去一个三角形后(截线不经过顶点),得到新多边形内角和为2160°,则原多边形的边数为(
)
A.13条
B.14条
C.15条
D.16条
6.下列说法中,错误的是(
)
A.一个三角形中至少有一个角不大于60°;
B.有一个外角是锐角的三角形是钝角三角形;
C.三角形的外角中必有两个角是钝角;
D.锐角三角形中两锐角的和必然小于60°。
C
A
D
当堂评价
1.一个三角形的三边长是整数,周长为5,则最小边为
;
2.木工师傅做完门框后,为防止变形,通常在角上钉一斜条,根据是
;
3.小明绕五边形各边走一圈,他共转了 度;
4.两多边形的边数分别是m,n条,且各多边形内角相等,又满足1/m+1/n=1/4,则各取一外角的和为
;
5.下列正多边形(1)正三角形(2)正方形(3)正五边形(4)正六边形,其中用一种正多边形能镶嵌成平面图案的是
。
1
三角形具有稳定性
360
90°
(1)、(2)、(4)
当堂评价
1.如图:D是△ABC中BC边上一点,试说明2AD<AB+BC+AC。
A
C
D
B
拓展思维
2.有一六边形,截去一三角形,内角和会发生
怎样变化?请画图说明。
内角和减少180°
内角和不变
内角和增加180°
拓展思维
https://www.21cnjy.com/help/help_extract.php
人教版
八年级上
三角形复习小结
三角形
与三角形有关的线段
三角形内角和
三角形外角和
三角形的边
高线
中线
角平分线
与三角形有关的角
内角与外角关系
三角形的定义、分类
知识回顾
多边形
定义
多边形的内外角和
知识回顾
A
C
B
1.
线段
叫做三角形的边。
2.点
叫做三角形的顶点。
3.
叫做三角形的内角,简称三角形的角。
1.三角形的定义:
AB、BC、CA
A、B、C
∠A、∠B、∠C
知识回顾
A
C
B
顶点是A、B、C的三角形记作:
a
c
b
读作:三角形ABC
三角形的边有时也用a、b、c来表示。
三角形用“△”符号表示
表示方法
△ABC
知识回顾
1.图中有几个三角形?用符号表示这些三角形。
2.以AB为边的三角形有哪些?
△ABC、△ABE
3.以E为顶点的三角形有哪些?
△ABE、△BCE、△CDE
5个:ΔABE、ΔBEC、
ΔECD、ΔABC、ΔBCD
A
B
E
C
D
小试牛刀
2.三角形的分类
锐角三角形
三角形
钝角三角形
(1)按角分
直角三角形
斜三角形
(2)按边分
腰和底不等的等腰三角形
三角形
等腰三角形
等边三角形
不等边三角形
知识回顾
1.三角形的三边关系:
(1)三角形两边的和大于第三边;
2.判断三条已知线段a、b、c能否
组成三角形。
当a最长,且有b+c>a时,就可构成三角形。
3.确定三角形第三边的取值范围:
两边之差<第三边<两边之和。
(2)三角形两边的差小于第三边。
知识回顾
三角形一个角的平分线与它的对边相交,这个角
的
之间的线段叫做三角形的角平分线。
连结三角形一个
的线段叫做三角形的中线。
从三角形的一个顶点向它的对边所在直线作垂线,_______________
的线段叫做三角形的高线。
1.三角形的高线定义:
顶点和垂足之间
2.三角形角平分线的定义:
顶点与交点
3.三角形的中线定义:
顶点与它对边中点
知识回顾
4.三角形的三条高线(或高线所在直线)交于一点(垂心)。
锐角三角形三条高线交于三角形内部一点,
直角三角形三条高线交于直角顶点,
钝角三角形三条高线所在直线交于三角形
外部一点。
5.三角形的三条中线交于三角形内部一点(重心)。
6.三角形的三条角平分线交于三角形内部一点(内心)。
知识回顾
1.三角形内角和定理
三角形的内角和等于180°,
直角三角形的两个锐角互余。
2.三角形外角和定理
三角形的外角和等于360°。
三角形的一个外角等于与它不相邻的两个内角的和。
3.三角形的外角与内角的关系
三角形的一个外角大于与它不相邻的任何一个内角。
知识回顾
三角形木架的形状不会改变,而四边形木架的形状会改变。
这就是说,三角形具有稳定性,而四边形没有稳定性。
知识回顾
三角形
长方形
六边形
四边形
八边形
在平面内,由一些不在同一条直线上的线段首尾顺次相接组成的图形叫做多边形。
你能仿照三角形的定义给出多边形的定义吗?
知识回顾
内角
对角线
对角线:连接多边形不相邻的两个顶点的线段。
可表示为:五边形ABCDE或五边形AEDCB
A
B
C
D
E
外角
1
知识回顾
请分别画出下列两个图形各边所在的直线,你能得到什么结论?
(1)
(2)
如图(1)这样,画出多边形的任何一条边所在的直线,整个多边形都在这条直线的同一侧,那么这个多边形就是凸多边形。本节我们只讨论凸多边形。
A
B
C
D
E
F
G
H
知识回顾
观察下面每个多边形的边、角有何特点?
在平面内,各个角都相等,各条边也都相等的多边形叫做正多边形。
知识回顾
n边形的内角和等于(n-2)·180°。
多边形的外角和都等于360°。
知识回顾
我们通过把多边形划分为若干个三角形,用三角形内角和去求多边形内角和,从而得到多边形的内角和公式为(n-2)×180°。这种化未知为已知的转化方法,必须在学习中逐渐掌握。由于多边形外角和为360°,与边数无关,所以常把多边形内角和的问题转化为外角和来处理。
知识回顾
1.在△ABC中,
(1)∠B=100°,∠A=∠C,则∠C=
;
(2)2∠A=∠B+∠C,∠A=
。
2.如图,______是△ACD的外角,
∠ADB=115°,∠CAD=80°则∠C=___。
40°
60°
35°
A
B
C
D
∠ADB
巩固练习
3.下列条件中能组成三角形的是(
)
A.5cm,13cm,7cm
B.3cm,5cm,9cm
C.14cm,9cm,6cm
D.5cm,6cm,11cm
C
4.三角形的两边为7cm和5cm,则第三边x的
范围是_____________。
2cm<x<12cm
巩固练习
5.如右图,AD是BC边上的高,BE是△ABD的角平分线,∠1=40°,∠2=30°,
则∠C=____,∠BED=_____
。
65°
60°
6.直角三角形的两个锐角相等,则每一个锐角等于_____度。
A
B
C
D
1
2
E
45
巩固练习
7.在△ABC中,∠A是∠B的2倍,∠C比∠A+∠B还大30°,则∠C的外角为_____度,这个三角形是____三角形。
75
钝角
8.如图,已知:AD是△ABC的中线,△ABC的面积为50cm2,则△ABD的面积是_______。
25cm2
A
B
C
D
巩固练习
解:由三角形两边之和大于第三边,
两边之差小于第三边得:
8-3
∴第三条边长为7cm、9cm。
1.已知两条线段的长分别是3cm、8cm,要想拼成一个三角形,且第三条线段a的长为奇数,问第三条线段应取多少长?
拓展训练
2.有一等腰三角形,一边的长是5cm,另一边的长是8cm,求它的周长。
解:(1)当腰长为5cm时,它的周长为:
5+5+8=18(cm)
(2)当腰长为8cm时,它的周长为:
8+8+5=21(cm)
∴这个三角形的周长为18cm或21cm。
拓展训练
1
D
C
A
B
3.已知∠B=42°,∠A+10°=∠1,∠ACD=64°,说明AB//CD。
拓展训练
A
B
C
X
1
2
3
4
4.已知∠1=∠2,∠3=∠4,∠A=100°,求X的值。
拓展训练
5.如图,△ABC中,∠A=∠ABD,∠C=∠BDC=∠ABC,求∠DBC的度数。
A
B
C
D
拓展训练
友情提示:
把图形内部七边形各角看作外部三角形外角,分析可得
6.求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数。
A
G
F
E
D
C
B
7×180°-2×360°=540°
拓展训练
1.三角形三个内角的度数分别是(x+y)°,(x-y)°,x°,且x>y>0,则该三角形有一个内角为( )
A.30°
B.45°
C.60°
D.90°
2.把14cm长的细铁丝截成三段,围成不是等边三角形的三角形,并且使三边长均为整数,那么( )
A.只有一种截法
B.只有两种截法
C.有三种截法
D.有四种截法
3.等腰三角形的腰长为a,底为X,则X的取值范围是( )
A.0<X<2a
B.0<X<a
C.0<X≤a
D.0<X≤2a
C
D
A
当堂评价
4.一个正多边形每一个内角都是120°,这个多边形是( )
A.正四边形
B.正五边形
C.正六边形
D.正七边形
5.一个多边形木板,截去一个三角形后(截线不经过顶点),得到新多边形内角和为2160°,则原多边形的边数为(
)
A.13条
B.14条
C.15条
D.16条
6.下列说法中,错误的是(
)
A.一个三角形中至少有一个角不大于60°;
B.有一个外角是锐角的三角形是钝角三角形;
C.三角形的外角中必有两个角是钝角;
D.锐角三角形中两锐角的和必然小于60°。
C
A
D
当堂评价
1.一个三角形的三边长是整数,周长为5,则最小边为
;
2.木工师傅做完门框后,为防止变形,通常在角上钉一斜条,根据是
;
3.小明绕五边形各边走一圈,他共转了 度;
4.两多边形的边数分别是m,n条,且各多边形内角相等,又满足1/m+1/n=1/4,则各取一外角的和为
;
5.下列正多边形(1)正三角形(2)正方形(3)正五边形(4)正六边形,其中用一种正多边形能镶嵌成平面图案的是
。
1
三角形具有稳定性
360
90°
(1)、(2)、(4)
当堂评价
1.如图:D是△ABC中BC边上一点,试说明2AD<AB+BC+AC。
A
C
D
B
拓展思维
2.有一六边形,截去一三角形,内角和会发生
怎样变化?请画图说明。
内角和减少180°
内角和不变
内角和增加180°
拓展思维
https://www.21cnjy.com/help/help_extract.php
