12.2三角形全等的的判定课后练习2021——2022学年 人教版八年级数学上册(Word版 含答案)
文档属性
| 名称 | 12.2三角形全等的的判定课后练习2021——2022学年 人教版八年级数学上册(Word版 含答案) | 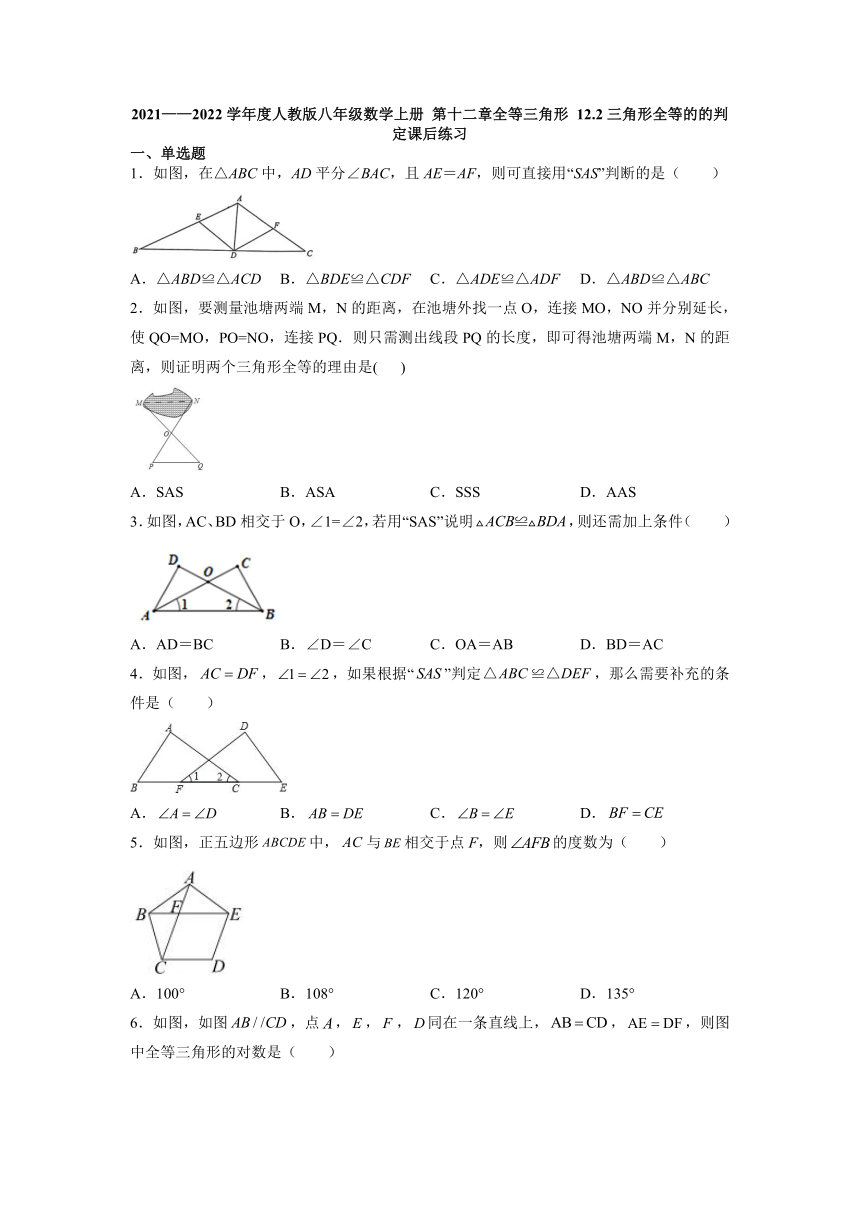 | |
| 格式 | docx | ||
| 文件大小 | 348.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-31 12:15:58 | ||
图片预览



文档简介
2021——2022学年度人教版八年级数学上册
第十二章全等三角形
12.2三角形全等的的判定课后练习
一、单选题
1.如图,在△ABC中,AD平分∠BAC,且AE=AF,则可直接用“SAS”判断的是( )
A.△ABD≌△ACD
B.△BDE≌△CDF
C.△ADE≌△ADF
D.△ABD≌△ABC
2.如图,要测量池塘两端M,N的距离,在池塘外找一点O,连接MO,NO并分别延长,使QO=MO,PO=NO,连接PQ.则只需测出线段PQ的长度,即可得池塘两端M,N的距离,则证明两个三角形全等的理由是(
??)
A.SAS
B.ASA
C.SSS
D.AAS
3.如图,AC、BD相交于O,∠1=∠2,若用“SAS”说明,则还需加上条件(
)
A.AD=BC
B.∠D=∠C
C.OA=AB
D.BD=AC
4.如图,,,如果根据“”判定,那么需要补充的条件是(
)
A.
B.
C.
D.
5.如图,正五边形中,与相交于点F,则的度数为( )
A.100°
B.108°
C.120°
D.135°
6.如图,如图,点,,,同在一条直线上,,,则图中全等三角形的对数是(
)
A.1对
B.2对
C.3对
D.4对
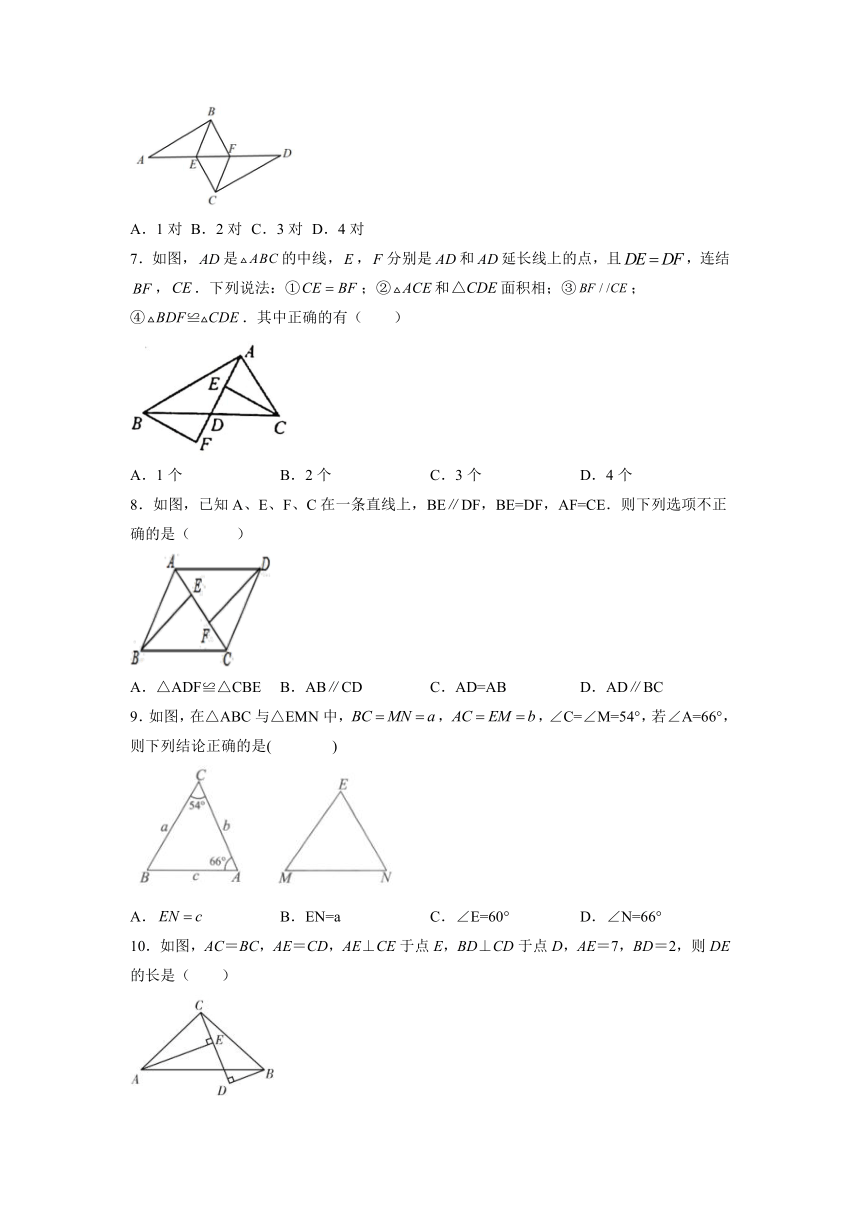
7.如图,是的中线,,分别是和延长线上的点,且,连结,.下列说法:①;②和面积相;③;④.其中正确的有(
)
A.1个
B.2个
C.3个
D.4个
8.如图,已知A、E、F、C在一条直线上,BE∥DF,BE=DF,AF=CE.则下列选项不正确的是(
)
A.△ADF≌△CBE
B.AB∥CD
C.AD=AB
D.AD∥BC
9.如图,在△ABC与△EMN中,,,∠C=∠M=54°,若∠A=66°,则下列结论正确的是(
)
A.
B.EN=a
C.∠E=60°
D.∠N=66°
10.如图,AC=BC,AE=CD,AE⊥CE于点E,BD⊥CD于点D,AE=7,BD=2,则DE的长是( )
A.7
B.5
C.3
D.2
二、填空题
11.如图,,于,于,且,在线段上,在射线上,若与全等,则__________.
12.如图,,要用“”判定,则可加上条件__________.
13.如图,AB=6cm,AC=4cm,BC=5cm,AE=AC,AD是△ABC的角平分线,则△BED的周长为_______.
14.如图,在中,已知,
,.若,则的度数为__________.
15.如图,在中,为线段上一动点(不与点重合),连接作,且连接,当时,______________________度.
三、解答题
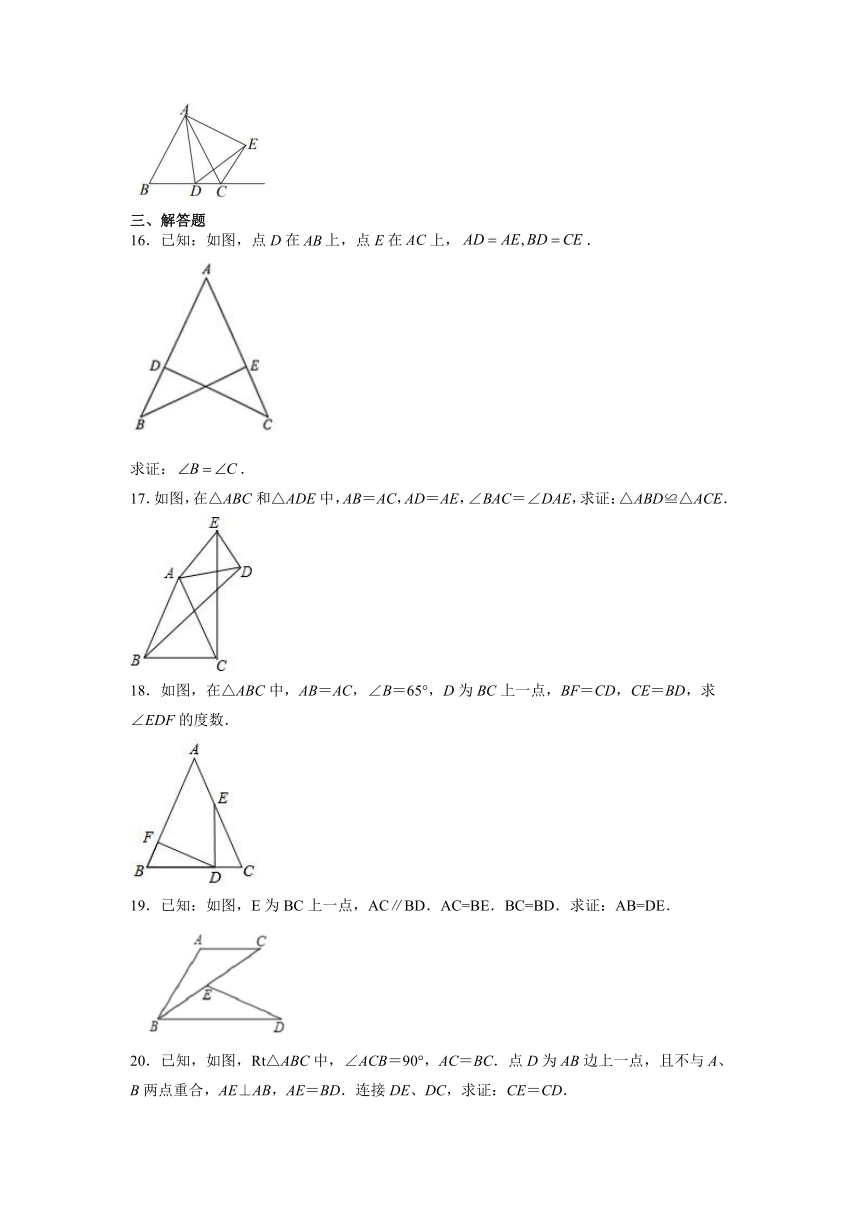
16.已知:如图,点D在上,点E在上,.
求证:.
17.如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,求证:△ABD≌△ACE.
18.如图,在△ABC中,AB=AC,∠B=65°,D为BC上一点,BF=CD,CE=BD,求∠EDF的度数.
19.已知:如图,E为BC上一点,AC∥BD.AC=BE.BC=BD.求证:AB=DE.
20.已知,如图,Rt△ABC中,∠ACB=90°,AC=BC.点D为AB边上一点,且不与A、B两点重合,AE⊥AB,AE=BD.连接DE、DC,求证:CE=CD.
21.如图,将两块含45°角的大小不同的直角三角板△COD和△AOB如图①摆放,连结AC,BD.
(1)如图①,猜想线段AC与BD存在怎样的数量关系和位置关系,请写出结论并证明;
(2)将图①中的△COD绕点O顺时针旋转一定的角度(如图②),连结AC,BD,其他条件不变,线段AC与BD还存在(1)中的关系吗?请写出结论并说明理由.
(3)将图①中的△COD绕点O逆时针旋转一定的角度(如图③),连结AC,BD,其他条件不变,线段AC与BD存在怎样的关系?请直接写出结论.
22.如图,A,B两点分别位于一个池塘的两侧,池塘西边有一座假山D,在的中点C处有一个雕塑,张倩从点A出发,沿直线一直向前经过点C走到点E,并使,然后她测量点E到假山D的距离,则的长度就是A,B两点之间的距离.
(1)你能说明张倩这样做的根据吗?
(2)如果张倩恰好未带测量工具,但是知道A和假山、雕塑分别相距200米、120米,你能帮助她确定的长度范围吗?
(3)在第(2)问的启发下,你能“已知三角形的一边和另一边上的中线,求第三边的范围吗?”请你解决下列问题:在中,是边的中线,,,求的取值范围.(要求画出图形)
23.有两个三角形,分别为和其中,.
(1)若按图①所示位置摆放,使得与重合,连接,则与CE
的数量关系是__________;
(2)在图①中延长BD交CE于点,如图②所示,求的度数;
(3)若按图③所示位置摆放,连接且与交于点F,请判断与之间的关系,并说明理由
【参考答案】
1.C
2.A
3.D
4.D
5.B
6.C
7.C
8.C
9.A
10.B
11.6或8
12.AD=BD
13.7cm.
14.70°
15.24
16.证明:∵AD=AE,BD=CE,
∴AB=AC,
在△ABE和△ACD中
,
∴△ABE≌△ACD(SAS),
∴∠B=∠C.
17.∵∠BAC=∠DAE,
∴∠BAC+∠CAD=∠DAE+∠CAD,
即∠EAC=∠DAB,
在△AEC和△ADB中,
∴△AEC≌△ADB(SAS).
18.∵AB=AC,
∴∠B=∠C,
在△FBD与△DCE中,
,
∴△FBD≌△DCE(SAS),
∴∠BFD=∠CDE,
∴∠B=180°-∠BDF-∠BFD=∠EDF=180°-∠BDF-∠CDE,
∵∠B=65°,
∴∠EDF=65°.
19.证明:∵AC∥BD,
∴∠ACB=∠DBC,
∵AC=BE,BC=BD,
∴△ABC≌△EDB,
∴AB=DE.
20.证明:∵∠ACB=90°,AC=BC,
∴∠B=∠CAD=45°.
∵AE⊥AB,
∴∠CAE+∠CAD=90°.
∴∠CAE=45°.
∴∠CAE=∠B.
在△ACE和△BCD中,,
∴△ACE≌△BCD(SAS),
∴CE=CD.
21.(1)AC=BD,AC⊥BD,
证明:延长BD交AC于点E.
∵△COD和△AOB均为等腰直角三角形,
∴OC=OD,OA=OB,
∠COA=∠BOD=90?,
∴△AOC≌△BOD(SAS),
∴AC=BD,
∴∠OAC=∠OBD,
∵∠ADE=∠BDO,
∴∠AED=∠BOD=90?,
∴AC⊥BD;
(2)存在,
证明:延长BD交AC于点F,交AO于点G.
∵△COD和△AOB均为等腰直角三角形,
∴OC=OD,OA=OB,
∠DOC=BOA=90?,
∵∠AOC=∠DOC-∠DOA,∠BOD=∠BOA-∠DOA,
∴∠AOC=∠BOD,
∴△AOC≌△BOD(SAS),
∴AC=BD,∠OAC=∠OBD,
∵∠AGF=∠BGO,
∴∠AFG=∠BOG=90?,
∴AC⊥BD;
(3)AC=BD,AC⊥BD.
证明:BD交AC于点H,AO于M,
∵△COD和△AOB均为等腰直角三角形,
∴OC=OD,OA=OB,
∠DOC=BOA=90?,
∵∠AOC=∠DOC+∠DOA,∠BOD=∠BOA+∠DOA,
∴∠AOC=∠BOD,
∴△AOC≌△BOD(SAS),
∴AC=BD,∠OAC=∠OBD,
∵∠AMH=∠BMO,
∴∠AHM=∠BOH=90?,
∴AC⊥BD.
22.解:(1)∵C是BD的中点,
∴DC=BC,
在△ABC和△EDC中,
,
△ABC≌△EDC(SAS),
∴AB=DE;
(2)连接AD,
∵AE-AD<DE<AE+AD,
又∵AD=200米,AC=120米,
∴AE=240米,
∴40米<DE<440米,
∵AB=DE,
∴40米<AB<440米,
(3)延长AD到E使得DE=AD,连接EC,
由(1)(2)可知AB=CE=6cm,AE=2AD=8cm,
∴AE-EC<AC<AE+EC,
∴2cm<AC<14cm.
23.解:(1)在△DAB和△EAC中,
,
∴△DAB≌△EAC(SAS),
∴BD=CE;
故答案为BD=CE;
(2)∵△DAB≌△EAC,
∴∠ECA=∠DBA,
∵∠FDC=∠ADB,
∴∠CFD=∠DAB=90°,
∴∠BFC=90°;
(3)BD与CE相互垂直,BD=CE.
理由如下:∵∠BAC=∠DAE,
∴∠BAC+∠CAD=∠DAE+∠CAD,
即∠BAD=∠CAE,
在△DAB和△EAC中,
,
∴△DAB≌△EAC(SAS),
∴∠ABD=∠ACE,BD=CE,
∵∠BAC=90°,
∴∠CBF+∠BCF=∠ABC+∠ACB=90°,
∴∠BFC=90°,
∴BD⊥CE.
第十二章全等三角形
12.2三角形全等的的判定课后练习
一、单选题
1.如图,在△ABC中,AD平分∠BAC,且AE=AF,则可直接用“SAS”判断的是( )
A.△ABD≌△ACD
B.△BDE≌△CDF
C.△ADE≌△ADF
D.△ABD≌△ABC
2.如图,要测量池塘两端M,N的距离,在池塘外找一点O,连接MO,NO并分别延长,使QO=MO,PO=NO,连接PQ.则只需测出线段PQ的长度,即可得池塘两端M,N的距离,则证明两个三角形全等的理由是(
??)
A.SAS
B.ASA
C.SSS
D.AAS
3.如图,AC、BD相交于O,∠1=∠2,若用“SAS”说明,则还需加上条件(
)
A.AD=BC
B.∠D=∠C
C.OA=AB
D.BD=AC
4.如图,,,如果根据“”判定,那么需要补充的条件是(
)
A.
B.
C.
D.
5.如图,正五边形中,与相交于点F,则的度数为( )
A.100°
B.108°
C.120°
D.135°
6.如图,如图,点,,,同在一条直线上,,,则图中全等三角形的对数是(
)
A.1对
B.2对
C.3对
D.4对
7.如图,是的中线,,分别是和延长线上的点,且,连结,.下列说法:①;②和面积相;③;④.其中正确的有(
)
A.1个
B.2个
C.3个
D.4个
8.如图,已知A、E、F、C在一条直线上,BE∥DF,BE=DF,AF=CE.则下列选项不正确的是(
)
A.△ADF≌△CBE
B.AB∥CD
C.AD=AB
D.AD∥BC
9.如图,在△ABC与△EMN中,,,∠C=∠M=54°,若∠A=66°,则下列结论正确的是(
)
A.
B.EN=a
C.∠E=60°
D.∠N=66°
10.如图,AC=BC,AE=CD,AE⊥CE于点E,BD⊥CD于点D,AE=7,BD=2,则DE的长是( )
A.7
B.5
C.3
D.2
二、填空题
11.如图,,于,于,且,在线段上,在射线上,若与全等,则__________.
12.如图,,要用“”判定,则可加上条件__________.
13.如图,AB=6cm,AC=4cm,BC=5cm,AE=AC,AD是△ABC的角平分线,则△BED的周长为_______.
14.如图,在中,已知,
,.若,则的度数为__________.
15.如图,在中,为线段上一动点(不与点重合),连接作,且连接,当时,______________________度.
三、解答题
16.已知:如图,点D在上,点E在上,.
求证:.
17.如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,求证:△ABD≌△ACE.
18.如图,在△ABC中,AB=AC,∠B=65°,D为BC上一点,BF=CD,CE=BD,求∠EDF的度数.
19.已知:如图,E为BC上一点,AC∥BD.AC=BE.BC=BD.求证:AB=DE.
20.已知,如图,Rt△ABC中,∠ACB=90°,AC=BC.点D为AB边上一点,且不与A、B两点重合,AE⊥AB,AE=BD.连接DE、DC,求证:CE=CD.
21.如图,将两块含45°角的大小不同的直角三角板△COD和△AOB如图①摆放,连结AC,BD.
(1)如图①,猜想线段AC与BD存在怎样的数量关系和位置关系,请写出结论并证明;
(2)将图①中的△COD绕点O顺时针旋转一定的角度(如图②),连结AC,BD,其他条件不变,线段AC与BD还存在(1)中的关系吗?请写出结论并说明理由.
(3)将图①中的△COD绕点O逆时针旋转一定的角度(如图③),连结AC,BD,其他条件不变,线段AC与BD存在怎样的关系?请直接写出结论.
22.如图,A,B两点分别位于一个池塘的两侧,池塘西边有一座假山D,在的中点C处有一个雕塑,张倩从点A出发,沿直线一直向前经过点C走到点E,并使,然后她测量点E到假山D的距离,则的长度就是A,B两点之间的距离.
(1)你能说明张倩这样做的根据吗?
(2)如果张倩恰好未带测量工具,但是知道A和假山、雕塑分别相距200米、120米,你能帮助她确定的长度范围吗?
(3)在第(2)问的启发下,你能“已知三角形的一边和另一边上的中线,求第三边的范围吗?”请你解决下列问题:在中,是边的中线,,,求的取值范围.(要求画出图形)
23.有两个三角形,分别为和其中,.
(1)若按图①所示位置摆放,使得与重合,连接,则与CE
的数量关系是__________;
(2)在图①中延长BD交CE于点,如图②所示,求的度数;
(3)若按图③所示位置摆放,连接且与交于点F,请判断与之间的关系,并说明理由
【参考答案】
1.C
2.A
3.D
4.D
5.B
6.C
7.C
8.C
9.A
10.B
11.6或8
12.AD=BD
13.7cm.
14.70°
15.24
16.证明:∵AD=AE,BD=CE,
∴AB=AC,
在△ABE和△ACD中
,
∴△ABE≌△ACD(SAS),
∴∠B=∠C.
17.∵∠BAC=∠DAE,
∴∠BAC+∠CAD=∠DAE+∠CAD,
即∠EAC=∠DAB,
在△AEC和△ADB中,
∴△AEC≌△ADB(SAS).
18.∵AB=AC,
∴∠B=∠C,
在△FBD与△DCE中,
,
∴△FBD≌△DCE(SAS),
∴∠BFD=∠CDE,
∴∠B=180°-∠BDF-∠BFD=∠EDF=180°-∠BDF-∠CDE,
∵∠B=65°,
∴∠EDF=65°.
19.证明:∵AC∥BD,
∴∠ACB=∠DBC,
∵AC=BE,BC=BD,
∴△ABC≌△EDB,
∴AB=DE.
20.证明:∵∠ACB=90°,AC=BC,
∴∠B=∠CAD=45°.
∵AE⊥AB,
∴∠CAE+∠CAD=90°.
∴∠CAE=45°.
∴∠CAE=∠B.
在△ACE和△BCD中,,
∴△ACE≌△BCD(SAS),
∴CE=CD.
21.(1)AC=BD,AC⊥BD,
证明:延长BD交AC于点E.
∵△COD和△AOB均为等腰直角三角形,
∴OC=OD,OA=OB,
∠COA=∠BOD=90?,
∴△AOC≌△BOD(SAS),
∴AC=BD,
∴∠OAC=∠OBD,
∵∠ADE=∠BDO,
∴∠AED=∠BOD=90?,
∴AC⊥BD;
(2)存在,
证明:延长BD交AC于点F,交AO于点G.
∵△COD和△AOB均为等腰直角三角形,
∴OC=OD,OA=OB,
∠DOC=BOA=90?,
∵∠AOC=∠DOC-∠DOA,∠BOD=∠BOA-∠DOA,
∴∠AOC=∠BOD,
∴△AOC≌△BOD(SAS),
∴AC=BD,∠OAC=∠OBD,
∵∠AGF=∠BGO,
∴∠AFG=∠BOG=90?,
∴AC⊥BD;
(3)AC=BD,AC⊥BD.
证明:BD交AC于点H,AO于M,
∵△COD和△AOB均为等腰直角三角形,
∴OC=OD,OA=OB,
∠DOC=BOA=90?,
∵∠AOC=∠DOC+∠DOA,∠BOD=∠BOA+∠DOA,
∴∠AOC=∠BOD,
∴△AOC≌△BOD(SAS),
∴AC=BD,∠OAC=∠OBD,
∵∠AMH=∠BMO,
∴∠AHM=∠BOH=90?,
∴AC⊥BD.
22.解:(1)∵C是BD的中点,
∴DC=BC,
在△ABC和△EDC中,
,
△ABC≌△EDC(SAS),
∴AB=DE;
(2)连接AD,
∵AE-AD<DE<AE+AD,
又∵AD=200米,AC=120米,
∴AE=240米,
∴40米<DE<440米,
∵AB=DE,
∴40米<AB<440米,
(3)延长AD到E使得DE=AD,连接EC,
由(1)(2)可知AB=CE=6cm,AE=2AD=8cm,
∴AE-EC<AC<AE+EC,
∴2cm<AC<14cm.
23.解:(1)在△DAB和△EAC中,
,
∴△DAB≌△EAC(SAS),
∴BD=CE;
故答案为BD=CE;
(2)∵△DAB≌△EAC,
∴∠ECA=∠DBA,
∵∠FDC=∠ADB,
∴∠CFD=∠DAB=90°,
∴∠BFC=90°;
(3)BD与CE相互垂直,BD=CE.
理由如下:∵∠BAC=∠DAE,
∴∠BAC+∠CAD=∠DAE+∠CAD,
即∠BAD=∠CAE,
在△DAB和△EAC中,
,
∴△DAB≌△EAC(SAS),
∴∠ABD=∠ACE,BD=CE,
∵∠BAC=90°,
∴∠CBF+∠BCF=∠ABC+∠ACB=90°,
∴∠BFC=90°,
∴BD⊥CE.
