2020—2021学年人教版数学七年级上册4.1.1 立体图形与平面图形同步练习(word解析版)
文档属性
| 名称 | 2020—2021学年人教版数学七年级上册4.1.1 立体图形与平面图形同步练习(word解析版) |

|
|
| 格式 | doc | ||
| 文件大小 | 300.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-31 13:24:23 | ||
图片预览


文档简介
4.1.1
立体图形与平面图形
一、选择题
1.下列说法错误的是( )
A.若棱柱的底面边长相等,则它的各个侧面的面积相等
B.正九棱柱有9条侧棱,9个侧面,侧面为长方形
C.长方体、正方体都是棱柱
D.三棱柱的侧面为三角形
2.下列说法中,正确的是( )
A.棱柱的侧面可以是三角形
B.有两个面平行,其余各面都是四边形的几何体叫棱柱
C.将直角三角形绕它的一边所在的直线旋转一周,形成的几何体一定是圆锥
D.棱台的侧棱所在的直线交于一点
3.下列命题正确的是( )
A.棱柱的底面一定是平行四边形
B.棱锥的底面一定是三角形
C.棱锥被平面分成的两部分不可能都是棱锥
D.棱柱被平面分成的两部分可以都是棱柱
4.对于棱锥,下列叙述正确的是( )
A.四棱锥共有四条棱
B.五棱锥共有五个面
C.六棱锥的顶点有六个
D.任何棱锥都只有一个底面
5.下列几种图形:①长方形,②梯形,③正方体,④圆柱,⑤圆锥,其中属于立体图形的是( )
A.①②③
B.③④⑤
C.③⑤
D.④⑤
6.如图(1)(2)是放置一个水管三叉接头,若从正面看这个接头时,看到图形如图(2)所示,则从上面看这个接头时,看到的图形是( )
A.
B.
C.
D.
7.太阳、西瓜、易拉罐、篮球、橡皮擦、书本中,形状类似圆柱的有( )
A.1个
B.2个
C.3个
D.4个
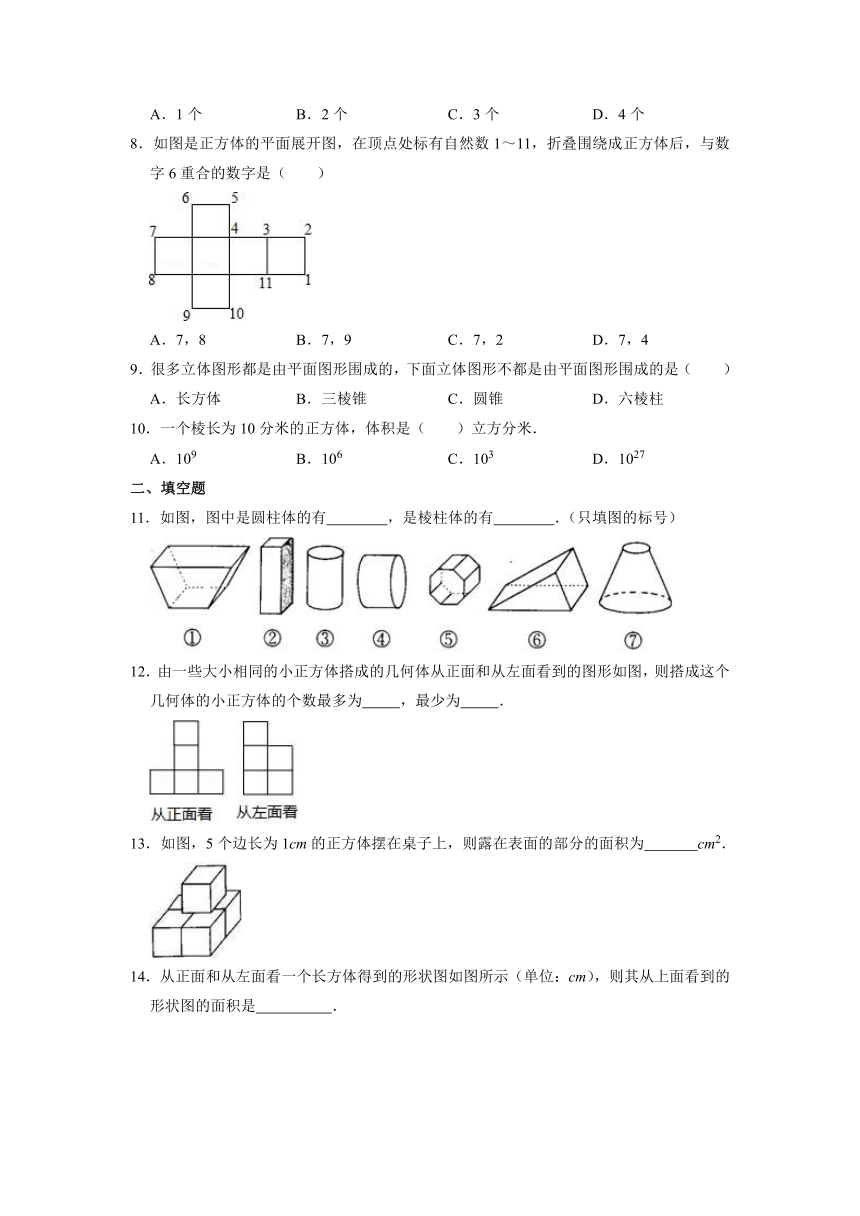
8.如图是正方体的平面展开图,在顶点处标有自然数1~11,折叠围绕成正方体后,与数字6重合的数字是( )
A.7,8
B.7,9
C.7,2
D.7,4
9.很多立体图形都是由平面图形围成的,下面立体图形不都是由平面图形围成的是( )
A.长方体
B.三棱锥
C.圆锥
D.六棱柱
10.一个棱长为10分米的正方体,体积是( )立方分米.
A.109
B.106
C.103
D.1027
二、填空题
11.如图,图中是圆柱体的有
,是棱柱体的有
.(只填图的标号)
12.由一些大小相同的小正方体搭成的几何体从正面和从左面看到的图形如图,则搭成这个几何体的小正方体的个数最多为
,最少为
.
13.如图,5个边长为1cm的正方体摆在桌子上,则露在表面的部分的面积为
cm2.
14.从正面和从左面看一个长方体得到的形状图如图所示(单位:cm),则其从上面看到的形状图的面积是
.
15.如图是一个正方体的侧面展开图,如果将它折叠成一个正方体后相对的面上的数相等,则图中x的值为
.
三、解答题
16.马小虎准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制成如图所示的拼接图形(实线部分),经折叠后发现还少一个面,请你在图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.(注:①只需添加一个符合要求的正方形;②添加的正方形用阴影表示)
17.如图所示的五棱柱的底面边长都是5cm,侧棱长12cm,它有多少个面?它的所有侧面的面积之和是多少?
18.如图所示是一个正方体的表面展开图,请回答下列问题:
(1)与面B、面C相对的面分别是
和
;
(2)若A=a3+a2b+3,B=﹣a2b+a3,C=a3﹣1,D=﹣(a2b+15),且相对两个面所表示的代数式的和都相等,求E、F代表的代数式.
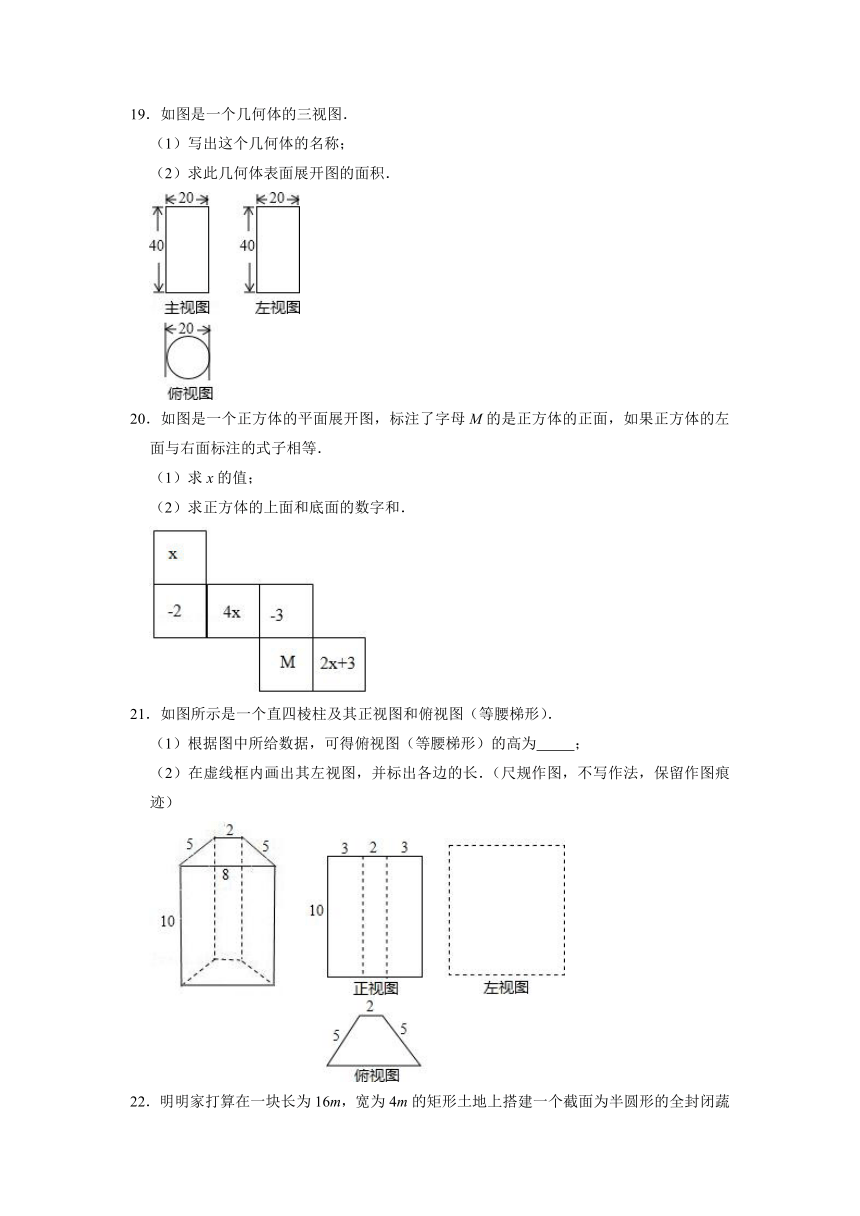
19.如图是一个几何体的三视图.
(1)写出这个几何体的名称;
(2)求此几何体表面展开图的面积.
20.如图是一个正方体的平面展开图,标注了字母M的是正方体的正面,如果正方体的左面与右面标注的式子相等.
(1)求x的值;
(2)求正方体的上面和底面的数字和.
21.如图所示是一个直四棱柱及其正视图和俯视图(等腰梯形).
(1)根据图中所给数据,可得俯视图(等腰梯形)的高为
;
(2)在虚线框内画出其左视图,并标出各边的长.(尺规作图,不写作法,保留作图痕迹)
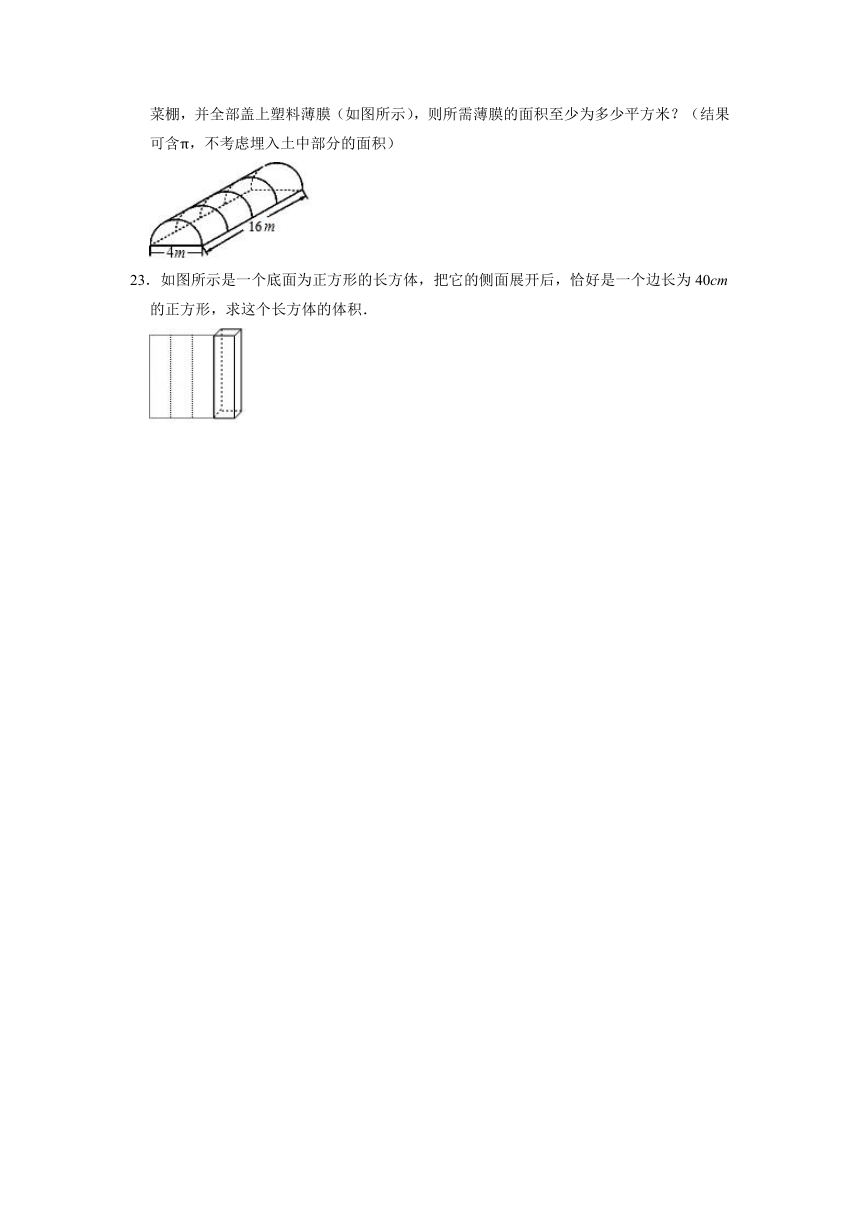
22.明明家打算在一块长为16m,宽为4m的矩形土地上搭建一个截面为半圆形的全封闭蔬菜棚,并全部盖上塑料薄膜(如图所示),则所需薄膜的面积至少为多少平方米?(结果可含π,不考虑埋入土中部分的面积)
23.如图所示是一个底面为正方形的长方体,把它的侧面展开后,恰好是一个边长为40cm的正方形,求这个长方体的体积.
参考答案与试题解析
一、选择题
1.下列说法错误的是( )
A.若棱柱的底面边长相等,则它的各个侧面的面积相等
B.正九棱柱有9条侧棱,9个侧面,侧面为长方形
C.长方体、正方体都是棱柱
D.三棱柱的侧面为三角形
【分析】根据立体图形的基本性质逐个判断即可求解.
【解答】解:(1)若棱柱的底面边长相等,则它的各个侧面的面积相等,这种说法正确,
(2)正九棱柱有9条侧棱,9个侧面,侧面为长方形,这种说法正确,
(3)长方体、正方体都是棱柱,这种说法正确,
(4)三棱柱的侧面为三角形,这种说法不正确,侧面为矩形,
故选:D.
2.下列说法中,正确的是( )
A.棱柱的侧面可以是三角形
B.有两个面平行,其余各面都是四边形的几何体叫棱柱
C.将直角三角形绕它的一边所在的直线旋转一周,形成的几何体一定是圆锥
D.棱台的侧棱所在的直线交于一点
【分析】根据棱柱、圆锥、棱台的结构特征解答.
【解答】解:对于A,∵棱柱的每个侧面都是平行四边形,所以A错误;
对于B,有两个面平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行的几何体叫棱柱,故选项B错误;
对于C,将直角三角形绕一边所在的直线旋转一周形成的几何体是圆锥,以斜边为轴,不是圆锥,所以C错误;
对于D,棱台是由棱锥用平行于底面的平面所截得的,故棱台的侧棱所在的直线交于一点,所以D正确.
故选:D.
3.下列命题正确的是( )
A.棱柱的底面一定是平行四边形
B.棱锥的底面一定是三角形
C.棱锥被平面分成的两部分不可能都是棱锥
D.棱柱被平面分成的两部分可以都是棱柱
【分析】根据棱柱和棱锥的有关知识判断即可.
【解答】解:A、棱柱的底面一定是平面多边形,不一定是平行四边形,原命题是错误;
B、棱柱的底面一定是平面多边形,不一定是三角形,原命题是错误;
C、棱锥被平面分成的两部分可能都是棱锥,原命题是错误;
D、棱柱被平面分成的两部分可以都是棱柱,是原命题正确;
故选:D.
4.对于棱锥,下列叙述正确的是( )
A.四棱锥共有四条棱
B.五棱锥共有五个面
C.六棱锥的顶点有六个
D.任何棱锥都只有一个底面
【分析】根据立体图形的性质逐个判断即可求解
【解答】解:(1)四棱锥共有四条棱,说法错误,有8条棱,
(2)五棱锥共有五个面,说法错误,有6个面,
(3)六棱锥的顶点有六个,说法错误,有7个顶点,
(4)任何棱锥都只有一个底面,说法正确,
故选:D.
5.下列几种图形:①长方形,②梯形,③正方体,④圆柱,⑤圆锥,其中属于立体图形的是( )
A.①②③
B.③④⑤
C.③⑤
D.④⑤
【分析】根据立体图形的定义解答.
【解答】解:①长方形是平面图形,
②梯形是平面图形,
③正方体是立体图形,
④圆柱是立体图形,
⑤圆锥是立体图形,
所以,属于立体图形的是③④⑤.
故选:B.
6.如图(1)(2)是放置一个水管三叉接头,若从正面看这个接头时,看到图形如图(2)所示,则从上面看这个接头时,看到的图形是( )
A.
B.
C.
D.
【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.
【解答】解:从上面看,可得到左边是一个圆,右边是长方形,一组对边与圆相接;
故选:A.
7.太阳、西瓜、易拉罐、篮球、橡皮擦、书本中,形状类似圆柱的有( )
A.1个
B.2个
C.3个
D.4个
【分析】根据圆柱的概念和定义知:圆柱由两个相等的圆形底面,一个封闭的曲面围成,据此进行判断即可.
【解答】解:形状类似圆柱的有易拉罐.
故选:A.
8.如图是正方体的平面展开图,在顶点处标有自然数1~11,折叠围绕成正方体后,与数字6重合的数字是( )
A.7,8
B.7,9
C.7,2
D.7,4
【分析】根据正方体的展开与折叠,
【解答】解:根据“间二,拐角邻面知”可得与A面相邻的面为B面、C面、D面、E面,
折叠后与数字6重合的数字为7,2,
故选:C.
9.很多立体图形都是由平面图形围成的,下面立体图形不都是由平面图形围成的是( )
A.长方体
B.三棱锥
C.圆锥
D.六棱柱
【分析】根据立体图形的基本性质即可求解.
【解答】解:(1)长方体是由平面围成,
(2)三棱锥是由平面围成,
(3)圆锥是由2个面围成,底面是平面,侧面是曲面,不都是由平面图形围成,
(4)六棱柱是由平面围成,
故选:C.
10.一个棱长为10分米的正方体,体积是( )立方分米.
A.109
B.106
C.103
D.1027
【分析】根据正方体的体积公式即可求解.
【解答】解:∵正方体的体积=a×a×a,
∴正方体的体积=10×10×10=103(立方分米),
故选:C.
二、填空题
11.如图,图中是圆柱体的有 ③,④ ,是棱柱体的有 ②,⑤,⑥ .(只填图的标号)
【分析】根据圆柱体以及棱柱体的特征进行判断即可.
【解答】解:图中是圆柱体的有③,④;
棱柱体的有②,⑤,⑥.
故答案为:③,④;②,⑤,⑥.
12.由一些大小相同的小正方体搭成的几何体从正面和从左面看到的图形如图,则搭成这个几何体的小正方体的个数最多为 9 ,最少为 7 .
【分析】根据三视图的知识,主视图是由5个小正方形组成,而左视图是由5个小正方形组成,故这个几何体的底层最少有4个,最多有6个小正方体,第2层有2个小正方体,第三层有1个.
【解答】解:根据左视图和主视图,这个几何体的底层最少有4个小正方体,最多有6个小正方体,
第二层有2个小正方体,第三层有1个,
所以最多有6+2+1=9个小正方体,最少有4+2+1=7个小正方体,
故答案为:9,7.
13.如图,5个边长为1cm的正方体摆在桌子上,则露在表面的部分的面积为 16 cm2.
【分析】5个边长为1cm的正方体的表面积之和是30cm2,因为被盖住的面有14个小正方形,其面积之和是14.
【解答】解:根据以上分析故露在表面的部分的面积为16cm2.故
答案为16.
14.从正面和从左面看一个长方体得到的形状图如图所示(单位:cm),则其从上面看到的形状图的面积是 12cm2 .
【分析】先根据从左面、从正面看到的形状图的相关数据可得,从正面看到的形状图是长为4宽为3的长方形,再根据长方形的面积公式计算即可.
【解答】解:根据从左面、从上面看到的形状图的相关数据可得:
从正面看到的形状图是长为4宽为3的长方形,
则从正面看到的形状图的面积是4×3=12cm2;
故答案为:12cm2.
15.如图是一个正方体的侧面展开图,如果将它折叠成一个正方体后相对的面上的数相等,则图中x的值为 7 .
【分析】正方体的平面展开图中,相对面的特点是中间必须间隔一个正方形,据此作答.
【解答】解:正方体的平面展开图中,相对面的特点是中间必须间隔一个正方形,所以与“x”字相对的字是7,故x=7.
三、解答题
16.马小虎准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制成如图所示的拼接图形(实线部分),经折叠后发现还少一个面,请你在图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.(注:①只需添加一个符合要求的正方形;②添加的正方形用阴影表示)
【分析】结合正方体的平面展开图的特征,只要折叠后能围成正方体即可,答案不唯一.
【解答】解:答案不唯一,如图.
17.如图所示的五棱柱的底面边长都是5cm,侧棱长12cm,它有多少个面?它的所有侧面的面积之和是多少?
【分析】结合图形、根据矩形的面积公式计算即可.
【解答】解:这个五棱柱有7个面,
它的所有侧面的面积之和是:5×12×5=300(cm2),
答:这个五棱柱有7个面,它的所有侧面的面积之和是300cm2.
18.如图所示是一个正方体的表面展开图,请回答下列问题:
(1)与面B、面C相对的面分别是 面F 和 面E ;
(2)若A=a3+a2b+3,B=﹣a2b+a3,C=a3﹣1,D=﹣(a2b+15),且相对两个面所表示的代数式的和都相等,求E、F代表的代数式.
【分析】(1)根据“相间Z端是对面”,可得B的对面为F,C的对面是E,
(2)根据相对两个面所表示的代数式的和都相等,三组对面为:A与D,B与F,C与E,列式计算即可.
【解答】解:(1)由“相间Z端是对面”,可得B的对面为F,C的对面是E,
故答案为:面F,面E.
(2)由题意得:A与D相对,B与F相对,C与E相对,
A+D=B+F=C+E
将A=a3+a2b+3,B=﹣a2b+a3,C=a3﹣1,D=﹣(a2b+15)代入得,
a3+a2b+3﹣(a2b+15)=﹣a2b+a3+F=a3﹣1+E,
∴F=a2b,
E=1,
19.如图是一个几何体的三视图.
(1)写出这个几何体的名称;
(2)求此几何体表面展开图的面积.
【分析】(1)由三视图的特征,可得这个几何体应该是圆柱柱;
(2)这个几何体的表面积应该等于两个圆的面积和一个矩形的面积和.
【解答】解:(1)根据题意,这个几何体是圆柱;
(2)该圆柱的高为40,底面直径为20,
表面积为:2×π×102+20π×40=1000π.
20.如图是一个正方体的平面展开图,标注了字母M的是正方体的正面,如果正方体的左面与右面标注的式子相等.
(1)求x的值;
(2)求正方体的上面和底面的数字和.
【分析】(1)正方体的表面展开图,相对的面之间一定相隔一个正方形确定出相对面,然后列出方程求解即可;
(2)确定出上面和底面上的两个数字﹣2和﹣3,然后相加即可.
【解答】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“M”与“x”是相对面,
“﹣2”与“﹣3”是相对面,
“4x”与“2x+3”是相对面,
(1)∵正方体的左面与右面标注的式子相等,
∴4x=2x+3,
解得x=1.5;
(2)∵标注了A字母的是正方体的正面,左面与右面标注的式子相等,
∴上面和底面上的两个数字﹣2和﹣3,
∴﹣2﹣3=﹣5.
21.如图所示是一个直四棱柱及其正视图和俯视图(等腰梯形).
(1)根据图中所给数据,可得俯视图(等腰梯形)的高为 4 ;
(2)在虚线框内画出其左视图,并标出各边的长.(尺规作图,不写作法,保留作图痕迹)
【分析】(1)过上底的顶点向对边引垂线组成直角三角形求解即可;
(2)易得左视图为长方形,宽等于(1)中算出的梯形的高,高等于正视图图中的10.
【解答】解:(1)4
作AE⊥BC于点E,则BE=(8﹣2)÷2=3,
∴高AE==4.
(2)
(6分).
22.明明家打算在一块长为16m,宽为4m的矩形土地上搭建一个截面为半圆形的全封闭蔬菜棚,并全部盖上塑料薄膜(如图所示),则所需薄膜的面积至少为多少平方米?(结果可含π,不考虑埋入土中部分的面积)
【分析】计算出直径为4m的圆的面积,即两头的“门”的面积;底面直径为4m,高为16m的圆柱体侧面积的一半,即“天棚”的面积,再求和即可.
【解答】解:π×()2+×4π×16
=4π+32π
=36π(m2),
答:所需薄膜的面积至少为36π平方米.
23.如图所示是一个底面为正方形的长方体,把它的侧面展开后,恰好是一个边长为40cm的正方形,求这个长方体的体积.
【分析】求出长方体的长、宽、高,即可求出长方体的体积.
【解答】解:根据题意可得,这个长方体的高为40cm,底面周长为40cm,
∵底面是正方形,
∴底面正方形的边长为10cm,
∴S底面=10×10=100
cm2,
∴V=SH=100×40=4000cm3,
答:这个长方体的体积是
4000cm3.
立体图形与平面图形
一、选择题
1.下列说法错误的是( )
A.若棱柱的底面边长相等,则它的各个侧面的面积相等
B.正九棱柱有9条侧棱,9个侧面,侧面为长方形
C.长方体、正方体都是棱柱
D.三棱柱的侧面为三角形
2.下列说法中,正确的是( )
A.棱柱的侧面可以是三角形
B.有两个面平行,其余各面都是四边形的几何体叫棱柱
C.将直角三角形绕它的一边所在的直线旋转一周,形成的几何体一定是圆锥
D.棱台的侧棱所在的直线交于一点
3.下列命题正确的是( )
A.棱柱的底面一定是平行四边形
B.棱锥的底面一定是三角形
C.棱锥被平面分成的两部分不可能都是棱锥
D.棱柱被平面分成的两部分可以都是棱柱
4.对于棱锥,下列叙述正确的是( )
A.四棱锥共有四条棱
B.五棱锥共有五个面
C.六棱锥的顶点有六个
D.任何棱锥都只有一个底面
5.下列几种图形:①长方形,②梯形,③正方体,④圆柱,⑤圆锥,其中属于立体图形的是( )
A.①②③
B.③④⑤
C.③⑤
D.④⑤
6.如图(1)(2)是放置一个水管三叉接头,若从正面看这个接头时,看到图形如图(2)所示,则从上面看这个接头时,看到的图形是( )
A.
B.
C.
D.
7.太阳、西瓜、易拉罐、篮球、橡皮擦、书本中,形状类似圆柱的有( )
A.1个
B.2个
C.3个
D.4个
8.如图是正方体的平面展开图,在顶点处标有自然数1~11,折叠围绕成正方体后,与数字6重合的数字是( )
A.7,8
B.7,9
C.7,2
D.7,4
9.很多立体图形都是由平面图形围成的,下面立体图形不都是由平面图形围成的是( )
A.长方体
B.三棱锥
C.圆锥
D.六棱柱
10.一个棱长为10分米的正方体,体积是( )立方分米.
A.109
B.106
C.103
D.1027
二、填空题
11.如图,图中是圆柱体的有
,是棱柱体的有
.(只填图的标号)
12.由一些大小相同的小正方体搭成的几何体从正面和从左面看到的图形如图,则搭成这个几何体的小正方体的个数最多为
,最少为
.
13.如图,5个边长为1cm的正方体摆在桌子上,则露在表面的部分的面积为
cm2.
14.从正面和从左面看一个长方体得到的形状图如图所示(单位:cm),则其从上面看到的形状图的面积是
.
15.如图是一个正方体的侧面展开图,如果将它折叠成一个正方体后相对的面上的数相等,则图中x的值为
.
三、解答题
16.马小虎准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制成如图所示的拼接图形(实线部分),经折叠后发现还少一个面,请你在图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.(注:①只需添加一个符合要求的正方形;②添加的正方形用阴影表示)
17.如图所示的五棱柱的底面边长都是5cm,侧棱长12cm,它有多少个面?它的所有侧面的面积之和是多少?
18.如图所示是一个正方体的表面展开图,请回答下列问题:
(1)与面B、面C相对的面分别是
和
;
(2)若A=a3+a2b+3,B=﹣a2b+a3,C=a3﹣1,D=﹣(a2b+15),且相对两个面所表示的代数式的和都相等,求E、F代表的代数式.
19.如图是一个几何体的三视图.
(1)写出这个几何体的名称;
(2)求此几何体表面展开图的面积.
20.如图是一个正方体的平面展开图,标注了字母M的是正方体的正面,如果正方体的左面与右面标注的式子相等.
(1)求x的值;
(2)求正方体的上面和底面的数字和.
21.如图所示是一个直四棱柱及其正视图和俯视图(等腰梯形).
(1)根据图中所给数据,可得俯视图(等腰梯形)的高为
;
(2)在虚线框内画出其左视图,并标出各边的长.(尺规作图,不写作法,保留作图痕迹)
22.明明家打算在一块长为16m,宽为4m的矩形土地上搭建一个截面为半圆形的全封闭蔬菜棚,并全部盖上塑料薄膜(如图所示),则所需薄膜的面积至少为多少平方米?(结果可含π,不考虑埋入土中部分的面积)
23.如图所示是一个底面为正方形的长方体,把它的侧面展开后,恰好是一个边长为40cm的正方形,求这个长方体的体积.
参考答案与试题解析
一、选择题
1.下列说法错误的是( )
A.若棱柱的底面边长相等,则它的各个侧面的面积相等
B.正九棱柱有9条侧棱,9个侧面,侧面为长方形
C.长方体、正方体都是棱柱
D.三棱柱的侧面为三角形
【分析】根据立体图形的基本性质逐个判断即可求解.
【解答】解:(1)若棱柱的底面边长相等,则它的各个侧面的面积相等,这种说法正确,
(2)正九棱柱有9条侧棱,9个侧面,侧面为长方形,这种说法正确,
(3)长方体、正方体都是棱柱,这种说法正确,
(4)三棱柱的侧面为三角形,这种说法不正确,侧面为矩形,
故选:D.
2.下列说法中,正确的是( )
A.棱柱的侧面可以是三角形
B.有两个面平行,其余各面都是四边形的几何体叫棱柱
C.将直角三角形绕它的一边所在的直线旋转一周,形成的几何体一定是圆锥
D.棱台的侧棱所在的直线交于一点
【分析】根据棱柱、圆锥、棱台的结构特征解答.
【解答】解:对于A,∵棱柱的每个侧面都是平行四边形,所以A错误;
对于B,有两个面平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行的几何体叫棱柱,故选项B错误;
对于C,将直角三角形绕一边所在的直线旋转一周形成的几何体是圆锥,以斜边为轴,不是圆锥,所以C错误;
对于D,棱台是由棱锥用平行于底面的平面所截得的,故棱台的侧棱所在的直线交于一点,所以D正确.
故选:D.
3.下列命题正确的是( )
A.棱柱的底面一定是平行四边形
B.棱锥的底面一定是三角形
C.棱锥被平面分成的两部分不可能都是棱锥
D.棱柱被平面分成的两部分可以都是棱柱
【分析】根据棱柱和棱锥的有关知识判断即可.
【解答】解:A、棱柱的底面一定是平面多边形,不一定是平行四边形,原命题是错误;
B、棱柱的底面一定是平面多边形,不一定是三角形,原命题是错误;
C、棱锥被平面分成的两部分可能都是棱锥,原命题是错误;
D、棱柱被平面分成的两部分可以都是棱柱,是原命题正确;
故选:D.
4.对于棱锥,下列叙述正确的是( )
A.四棱锥共有四条棱
B.五棱锥共有五个面
C.六棱锥的顶点有六个
D.任何棱锥都只有一个底面
【分析】根据立体图形的性质逐个判断即可求解
【解答】解:(1)四棱锥共有四条棱,说法错误,有8条棱,
(2)五棱锥共有五个面,说法错误,有6个面,
(3)六棱锥的顶点有六个,说法错误,有7个顶点,
(4)任何棱锥都只有一个底面,说法正确,
故选:D.
5.下列几种图形:①长方形,②梯形,③正方体,④圆柱,⑤圆锥,其中属于立体图形的是( )
A.①②③
B.③④⑤
C.③⑤
D.④⑤
【分析】根据立体图形的定义解答.
【解答】解:①长方形是平面图形,
②梯形是平面图形,
③正方体是立体图形,
④圆柱是立体图形,
⑤圆锥是立体图形,
所以,属于立体图形的是③④⑤.
故选:B.
6.如图(1)(2)是放置一个水管三叉接头,若从正面看这个接头时,看到图形如图(2)所示,则从上面看这个接头时,看到的图形是( )
A.
B.
C.
D.
【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.
【解答】解:从上面看,可得到左边是一个圆,右边是长方形,一组对边与圆相接;
故选:A.
7.太阳、西瓜、易拉罐、篮球、橡皮擦、书本中,形状类似圆柱的有( )
A.1个
B.2个
C.3个
D.4个
【分析】根据圆柱的概念和定义知:圆柱由两个相等的圆形底面,一个封闭的曲面围成,据此进行判断即可.
【解答】解:形状类似圆柱的有易拉罐.
故选:A.
8.如图是正方体的平面展开图,在顶点处标有自然数1~11,折叠围绕成正方体后,与数字6重合的数字是( )
A.7,8
B.7,9
C.7,2
D.7,4
【分析】根据正方体的展开与折叠,
【解答】解:根据“间二,拐角邻面知”可得与A面相邻的面为B面、C面、D面、E面,
折叠后与数字6重合的数字为7,2,
故选:C.
9.很多立体图形都是由平面图形围成的,下面立体图形不都是由平面图形围成的是( )
A.长方体
B.三棱锥
C.圆锥
D.六棱柱
【分析】根据立体图形的基本性质即可求解.
【解答】解:(1)长方体是由平面围成,
(2)三棱锥是由平面围成,
(3)圆锥是由2个面围成,底面是平面,侧面是曲面,不都是由平面图形围成,
(4)六棱柱是由平面围成,
故选:C.
10.一个棱长为10分米的正方体,体积是( )立方分米.
A.109
B.106
C.103
D.1027
【分析】根据正方体的体积公式即可求解.
【解答】解:∵正方体的体积=a×a×a,
∴正方体的体积=10×10×10=103(立方分米),
故选:C.
二、填空题
11.如图,图中是圆柱体的有 ③,④ ,是棱柱体的有 ②,⑤,⑥ .(只填图的标号)
【分析】根据圆柱体以及棱柱体的特征进行判断即可.
【解答】解:图中是圆柱体的有③,④;
棱柱体的有②,⑤,⑥.
故答案为:③,④;②,⑤,⑥.
12.由一些大小相同的小正方体搭成的几何体从正面和从左面看到的图形如图,则搭成这个几何体的小正方体的个数最多为 9 ,最少为 7 .
【分析】根据三视图的知识,主视图是由5个小正方形组成,而左视图是由5个小正方形组成,故这个几何体的底层最少有4个,最多有6个小正方体,第2层有2个小正方体,第三层有1个.
【解答】解:根据左视图和主视图,这个几何体的底层最少有4个小正方体,最多有6个小正方体,
第二层有2个小正方体,第三层有1个,
所以最多有6+2+1=9个小正方体,最少有4+2+1=7个小正方体,
故答案为:9,7.
13.如图,5个边长为1cm的正方体摆在桌子上,则露在表面的部分的面积为 16 cm2.
【分析】5个边长为1cm的正方体的表面积之和是30cm2,因为被盖住的面有14个小正方形,其面积之和是14.
【解答】解:根据以上分析故露在表面的部分的面积为16cm2.故
答案为16.
14.从正面和从左面看一个长方体得到的形状图如图所示(单位:cm),则其从上面看到的形状图的面积是 12cm2 .
【分析】先根据从左面、从正面看到的形状图的相关数据可得,从正面看到的形状图是长为4宽为3的长方形,再根据长方形的面积公式计算即可.
【解答】解:根据从左面、从上面看到的形状图的相关数据可得:
从正面看到的形状图是长为4宽为3的长方形,
则从正面看到的形状图的面积是4×3=12cm2;
故答案为:12cm2.
15.如图是一个正方体的侧面展开图,如果将它折叠成一个正方体后相对的面上的数相等,则图中x的值为 7 .
【分析】正方体的平面展开图中,相对面的特点是中间必须间隔一个正方形,据此作答.
【解答】解:正方体的平面展开图中,相对面的特点是中间必须间隔一个正方形,所以与“x”字相对的字是7,故x=7.
三、解答题
16.马小虎准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制成如图所示的拼接图形(实线部分),经折叠后发现还少一个面,请你在图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.(注:①只需添加一个符合要求的正方形;②添加的正方形用阴影表示)
【分析】结合正方体的平面展开图的特征,只要折叠后能围成正方体即可,答案不唯一.
【解答】解:答案不唯一,如图.
17.如图所示的五棱柱的底面边长都是5cm,侧棱长12cm,它有多少个面?它的所有侧面的面积之和是多少?
【分析】结合图形、根据矩形的面积公式计算即可.
【解答】解:这个五棱柱有7个面,
它的所有侧面的面积之和是:5×12×5=300(cm2),
答:这个五棱柱有7个面,它的所有侧面的面积之和是300cm2.
18.如图所示是一个正方体的表面展开图,请回答下列问题:
(1)与面B、面C相对的面分别是 面F 和 面E ;
(2)若A=a3+a2b+3,B=﹣a2b+a3,C=a3﹣1,D=﹣(a2b+15),且相对两个面所表示的代数式的和都相等,求E、F代表的代数式.
【分析】(1)根据“相间Z端是对面”,可得B的对面为F,C的对面是E,
(2)根据相对两个面所表示的代数式的和都相等,三组对面为:A与D,B与F,C与E,列式计算即可.
【解答】解:(1)由“相间Z端是对面”,可得B的对面为F,C的对面是E,
故答案为:面F,面E.
(2)由题意得:A与D相对,B与F相对,C与E相对,
A+D=B+F=C+E
将A=a3+a2b+3,B=﹣a2b+a3,C=a3﹣1,D=﹣(a2b+15)代入得,
a3+a2b+3﹣(a2b+15)=﹣a2b+a3+F=a3﹣1+E,
∴F=a2b,
E=1,
19.如图是一个几何体的三视图.
(1)写出这个几何体的名称;
(2)求此几何体表面展开图的面积.
【分析】(1)由三视图的特征,可得这个几何体应该是圆柱柱;
(2)这个几何体的表面积应该等于两个圆的面积和一个矩形的面积和.
【解答】解:(1)根据题意,这个几何体是圆柱;
(2)该圆柱的高为40,底面直径为20,
表面积为:2×π×102+20π×40=1000π.
20.如图是一个正方体的平面展开图,标注了字母M的是正方体的正面,如果正方体的左面与右面标注的式子相等.
(1)求x的值;
(2)求正方体的上面和底面的数字和.
【分析】(1)正方体的表面展开图,相对的面之间一定相隔一个正方形确定出相对面,然后列出方程求解即可;
(2)确定出上面和底面上的两个数字﹣2和﹣3,然后相加即可.
【解答】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“M”与“x”是相对面,
“﹣2”与“﹣3”是相对面,
“4x”与“2x+3”是相对面,
(1)∵正方体的左面与右面标注的式子相等,
∴4x=2x+3,
解得x=1.5;
(2)∵标注了A字母的是正方体的正面,左面与右面标注的式子相等,
∴上面和底面上的两个数字﹣2和﹣3,
∴﹣2﹣3=﹣5.
21.如图所示是一个直四棱柱及其正视图和俯视图(等腰梯形).
(1)根据图中所给数据,可得俯视图(等腰梯形)的高为 4 ;
(2)在虚线框内画出其左视图,并标出各边的长.(尺规作图,不写作法,保留作图痕迹)
【分析】(1)过上底的顶点向对边引垂线组成直角三角形求解即可;
(2)易得左视图为长方形,宽等于(1)中算出的梯形的高,高等于正视图图中的10.
【解答】解:(1)4
作AE⊥BC于点E,则BE=(8﹣2)÷2=3,
∴高AE==4.
(2)
(6分).
22.明明家打算在一块长为16m,宽为4m的矩形土地上搭建一个截面为半圆形的全封闭蔬菜棚,并全部盖上塑料薄膜(如图所示),则所需薄膜的面积至少为多少平方米?(结果可含π,不考虑埋入土中部分的面积)
【分析】计算出直径为4m的圆的面积,即两头的“门”的面积;底面直径为4m,高为16m的圆柱体侧面积的一半,即“天棚”的面积,再求和即可.
【解答】解:π×()2+×4π×16
=4π+32π
=36π(m2),
答:所需薄膜的面积至少为36π平方米.
23.如图所示是一个底面为正方形的长方体,把它的侧面展开后,恰好是一个边长为40cm的正方形,求这个长方体的体积.
【分析】求出长方体的长、宽、高,即可求出长方体的体积.
【解答】解:根据题意可得,这个长方体的高为40cm,底面周长为40cm,
∵底面是正方形,
∴底面正方形的边长为10cm,
∴S底面=10×10=100
cm2,
∴V=SH=100×40=4000cm3,
答:这个长方体的体积是
4000cm3.
