2021-2022学年人教版九年级数学上册第二十二章二次函数复习课件(29张ppt)
文档属性
| 名称 | 2021-2022学年人教版九年级数学上册第二十二章二次函数复习课件(29张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 12.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-31 19:28:42 | ||
图片预览




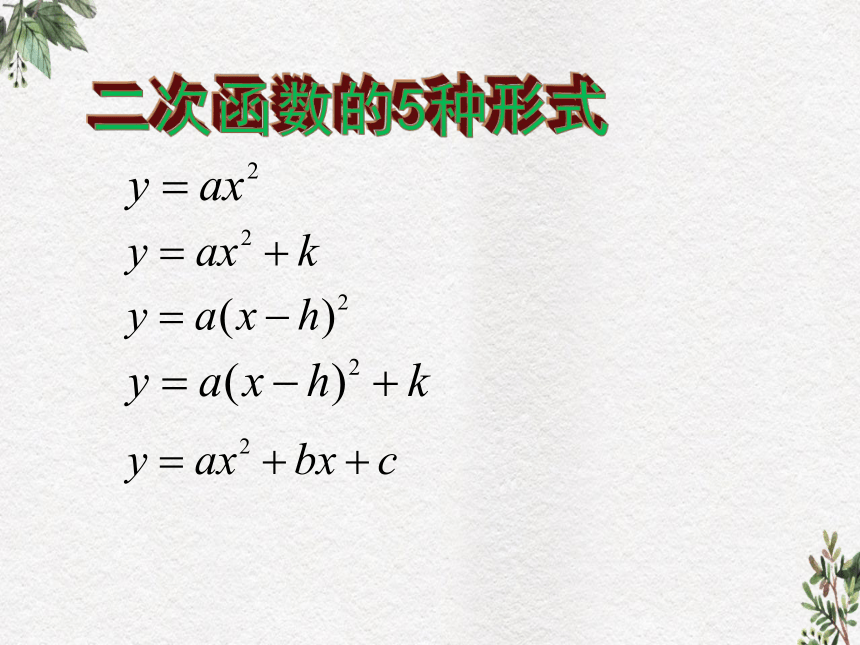

文档简介
(共29张PPT)
二次函数复习课
方老师
九年级数学上
知识点清单
二次函数的概念
5个基本的二次函数图像与性质
图像平移的规律
3种基本方法求二次函数解析式
与一元二次方程及不等式的关系
几种常见的应用题型
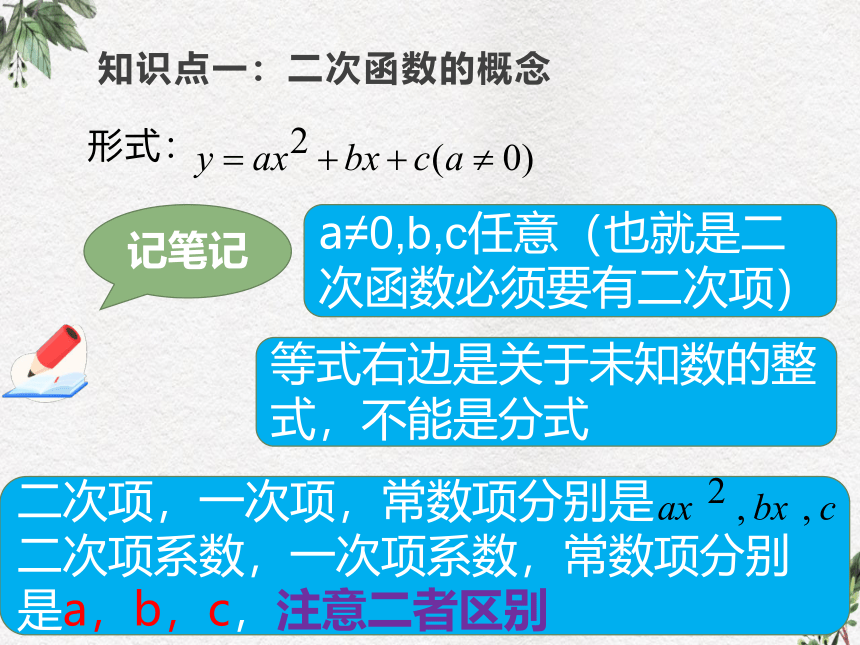
知识点一:二次函数的概念
形式:
记笔记
a≠0,b,c任意(也就是二次函数必须要有二次项)
等式右边是关于未知数的整式,不能是分式
二次项,一次项,常数项分别是
二次项系数,一次项系数,常数项分别是a,b,c,注意二者区别
典型题型1
下列选项中,是二次函数的有(
)
①
②
③
④
⑤
典型题型2
在函数
中,
(1)当a为何值时,该函数为二次函数?
(2)当a为何值时,该函数为一次函数?
二次函数的图像和性质一般从5个方面研究
图像
开口方向和开口大小
顶点坐标
对称轴
最值
单调性
知识点二:二次函数的图像和性质
接下来同学们
先自己来总结!
二次函数的5种形式
y=ax2
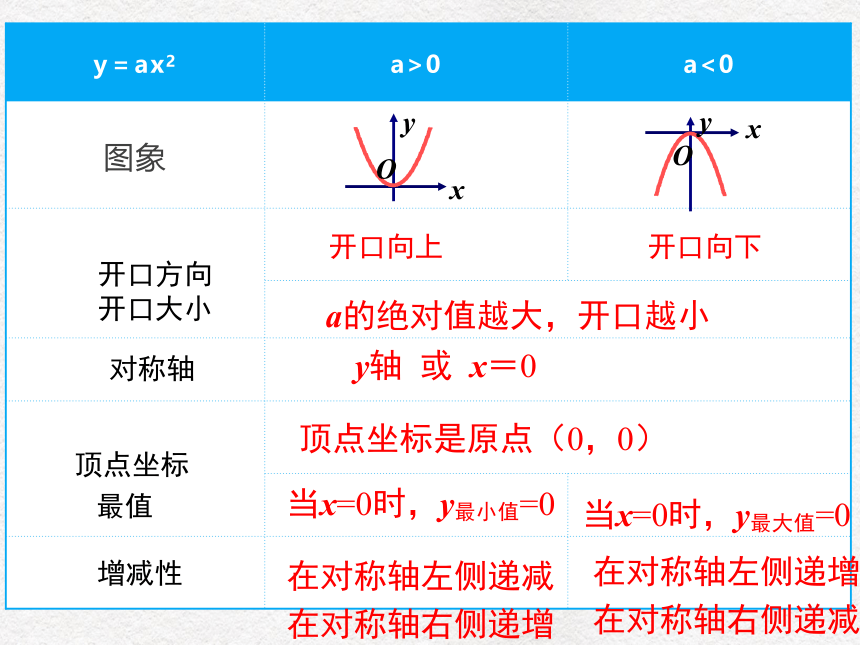
a>0
a<0
图象
开口方向开口大小
对称轴
顶点坐标
最值
增减性
开口向上
开口向下
a的绝对值越大,开口越小
y轴
或
x=0
当x=0时,y最小值=0
当x=0时,y最大值=0
在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
y
O
x
y
O
x
顶点坐标是原点(0,0)
记忆方法
同学们在记性质的时候,记住以下几点,更易掌握!
所有二次函数的开口大小和方向都取决于a
顶点坐标,对称轴,最值一起记,顶点横坐标就是对称轴,纵坐标即为最值,掌握一个顶点坐标,其它两个也就记住了
所有二次函数的增减性都是在对称轴两边讨论,对称轴掌握了,结合开口方向,增减性也就容易讨论了!
其他函数的图像都可以由
的图像平移得到,因此掌握图像的平移规律,我们就可以得到其它函数的图像和性质了
上下平移
左
右
平
移
上下左右平移
配方
顶点式
一般式
请同学们结合函数之间的平移规律,自己总结余下4个函数的图像和性质
y=ax2+k
a>0,k>0
a>0,
k<0
a<0,k>0
a<0,
k<0
图象
开口方向
对称轴
顶点坐标
最值
函数的增减性
向上
向下
y轴(直线x=0)
y轴(直线x=0)
(0,c)
(0,c)
当x<0时,y随x增大而减小;当x>0时,y随x增大而增大.
当x<0时,y随x增大而增大;当x>0时,y随x增大而减小.
x=0时,y最小值=c
x=0时,y最大值=c
y=a(x-h)2
a>0
a<0
开口方向
向上
向下
对称轴
直线x=h
直线x=h
顶点坐标
(h,0)
(h,0)
最值
当x=h时,y最小值=0
当x=h时,y最大值=0
增减性
当x<h时,y随x的增大而减小;x>h时,y随x的增大而增大.
当x>h时,y随x的增大而减小;x<h时,y随x的增大而增大.
请同学们画出该函数的几种图像
字母符号
图象的特征
a>0
开口_____________________
a<0
开口_____________________
b=0
对称轴为_____轴
a、b同号
对称轴在y轴的____侧
a、b异号
对称轴在y轴的____侧
c=0
经过原点
c>0
与y轴交于_____半轴
c<0
与y轴交于_____半轴
向上
向下
y
左
右
正
负
二次函数y=ax2+bx+c的图象与a、b、c的关系
典型题型1
二次函数y=ax2+bx+c的图象与a、b、c的关系
-1
O
x=1
y
x
已知二次函数
(a≠0)
的图像如图所示,有下列结论:
①abc>0;
②2a+b=0;
③a-b+c=0;
④c=-3a;
其中正确的有(
)(填序号)
在同一直角坐标系中,函数
和
(
是常数,且
)的图象可能是(
)
典型题型3
二次函数与一次函数的综合
x
y
O
A.
x
y
O
B.
x
y
O
C.
x
y
O
D.
若A(-4,y1),B(-3,y2),C(1,y3)为二次函数y=x2+4x-5的图象上的三点,则y1,y2,y3的大小关系是(
)
A、y1<y2<y3
B、y2<y1<y3
C、y3<y1<y2
D、y1<y3<y2
典型题型2
二次函数函数值大小比较
看到题目里有比大小,涉及到的知识点就是二次函数对称轴
把x的值直接代入解析式
根据图像的对称性,把所有点移到对称轴一边,再比较
两种做题方法
将二次函数y=x2+3x+4向左平移2个单位长度,再向上平移3个单位长度得到的解析式为
典型题型4
二次函数图像的平移
平移规律
左右平移改变x,即含有x的项都要变,左+右-
上下平移改变y,即直接在等式后面加减,上+下-
知识点三:二次函数的解析式求法
1.一般式法:y=ax2+bx+c
(a≠
0)
2.顶点法:y=a(x-h)2+k(a≠0)
3.交点法:y=a(x-x1)(x-x2)(a≠0)
三种解析式的适用条件
已知3个点的坐标,可以用一般式求解析式
已知顶点坐标和其它任意两点坐标,可以用顶点式求解析式
已知与x轴的两个点的坐标以及其它任意一个点的坐标,可用交点式求解析式(也可用一般式)
典型题型
若一抛物线形状与y=-5x2+2相同,顶点坐标是(4,-2),则其解析式是_____________.
已知关于x的二次函数,当x=-1时,函数值为10,当x=1时,函数值为4,当x=2时,函数值为7,则其解析式是_____________.
判别式△=b2-4ac
二次函数y=ax2+bx+c
(a>0)
的图象
一元二次方程ax2+bx+c=0
(a≠0)的根
不等式ax2+bx+c>0(a>0)的解集
不等式ax2+bx+c<0(a>0)的解集
x2
x1
x
y
o
O
x1=
x2
x
y
x
O
x
y
x
△>0
△=0
△<0
x1
;
x2
x1
=x2
=-b/2a
没有实数根
xx2
x
≠
x1的一切实数
所有实数
x1无解
无解
知识点四:二次函数与一元二次方程以及
一元二次不等式的关系
二次函数y=kx2-6x+3的图象与x轴有交点,则k的取值范围是( )
A.k<3
B.k<3且k≠0
C.k≤3
D.k≤3且k≠0
典型题型1
如果这题把二次函数中
二次这个前提去掉,
答案还会一样吗?
已知二次函数y=2(x-1)(x-m-3)(m为常数)。
(1)求证:不论m为何值,该函数的图像与x轴总有公共点。
(2)当m取何值时,该函数的图像与y轴的交点在x轴上方?
典型题型2
如图,
某中学要在教学楼后面的空地上用40米长的竹篱笆围出一个矩形地块作生物园,
矩形的一边用教学楼的外墙,其余三边用竹篱笆.
设矩形的宽为x,面积为y.
(1)
求y与x的函数关系式,并求自变量的取值范围;
(2)
生物园的面积能否达到210平方米?说明理由.
知识点五:二次函数的几种常见应用题型
第一类:面积最值问题
教学楼
x
第二类:利润最值问题
小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元,调研发现:
①盆景每增加1盆,盆景的平均每盆利润减少2元;每减少1盆,盆景的平均每盆利润增加2元;②花卉的平均每盆利润始终不变.
小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x盆,第二期盆景与花卉售完后的利润分别为W1,W2(单位:元)
(1)用含x的代数式分别表示W1,W2;
(2)当x取何值时,第二期培植的盆景与花卉售完后获得的总利润W最大,最大总利润是多少?
某学校初三年级的一场篮球比赛中,如图,队员甲正在投篮,已知球出手时距地面
米,与篮框中心的水平距离为7米,当球出手后水平距离为4米时到达最大高度4米,设篮球运行轨迹为抛物线,篮框距地面3米.
(1)建立如图所示的平面直角坐标系,问此球能否准确投中?
第三类:抛物问题
(2)此时,若对方队员乙在甲面前1米处跳起盖帽拦截,已知乙的最大摸高为3.1米,那么他能否获得成功?
A
B
C
今天也是粉色的心情
每天都是喜欢的自己
二次函数复习课
方老师
九年级数学上
知识点清单
二次函数的概念
5个基本的二次函数图像与性质
图像平移的规律
3种基本方法求二次函数解析式
与一元二次方程及不等式的关系
几种常见的应用题型
知识点一:二次函数的概念
形式:
记笔记
a≠0,b,c任意(也就是二次函数必须要有二次项)
等式右边是关于未知数的整式,不能是分式
二次项,一次项,常数项分别是
二次项系数,一次项系数,常数项分别是a,b,c,注意二者区别
典型题型1
下列选项中,是二次函数的有(
)
①
②
③
④
⑤
典型题型2
在函数
中,
(1)当a为何值时,该函数为二次函数?
(2)当a为何值时,该函数为一次函数?
二次函数的图像和性质一般从5个方面研究
图像
开口方向和开口大小
顶点坐标
对称轴
最值
单调性
知识点二:二次函数的图像和性质
接下来同学们
先自己来总结!
二次函数的5种形式
y=ax2
a>0
a<0
图象
开口方向开口大小
对称轴
顶点坐标
最值
增减性
开口向上
开口向下
a的绝对值越大,开口越小
y轴
或
x=0
当x=0时,y最小值=0
当x=0时,y最大值=0
在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
y
O
x
y
O
x
顶点坐标是原点(0,0)
记忆方法
同学们在记性质的时候,记住以下几点,更易掌握!
所有二次函数的开口大小和方向都取决于a
顶点坐标,对称轴,最值一起记,顶点横坐标就是对称轴,纵坐标即为最值,掌握一个顶点坐标,其它两个也就记住了
所有二次函数的增减性都是在对称轴两边讨论,对称轴掌握了,结合开口方向,增减性也就容易讨论了!
其他函数的图像都可以由
的图像平移得到,因此掌握图像的平移规律,我们就可以得到其它函数的图像和性质了
上下平移
左
右
平
移
上下左右平移
配方
顶点式
一般式
请同学们结合函数之间的平移规律,自己总结余下4个函数的图像和性质
y=ax2+k
a>0,k>0
a>0,
k<0
a<0,k>0
a<0,
k<0
图象
开口方向
对称轴
顶点坐标
最值
函数的增减性
向上
向下
y轴(直线x=0)
y轴(直线x=0)
(0,c)
(0,c)
当x<0时,y随x增大而减小;当x>0时,y随x增大而增大.
当x<0时,y随x增大而增大;当x>0时,y随x增大而减小.
x=0时,y最小值=c
x=0时,y最大值=c
y=a(x-h)2
a>0
a<0
开口方向
向上
向下
对称轴
直线x=h
直线x=h
顶点坐标
(h,0)
(h,0)
最值
当x=h时,y最小值=0
当x=h时,y最大值=0
增减性
当x<h时,y随x的增大而减小;x>h时,y随x的增大而增大.
当x>h时,y随x的增大而减小;x<h时,y随x的增大而增大.
请同学们画出该函数的几种图像
字母符号
图象的特征
a>0
开口_____________________
a<0
开口_____________________
b=0
对称轴为_____轴
a、b同号
对称轴在y轴的____侧
a、b异号
对称轴在y轴的____侧
c=0
经过原点
c>0
与y轴交于_____半轴
c<0
与y轴交于_____半轴
向上
向下
y
左
右
正
负
二次函数y=ax2+bx+c的图象与a、b、c的关系
典型题型1
二次函数y=ax2+bx+c的图象与a、b、c的关系
-1
O
x=1
y
x
已知二次函数
(a≠0)
的图像如图所示,有下列结论:
①abc>0;
②2a+b=0;
③a-b+c=0;
④c=-3a;
其中正确的有(
)(填序号)
在同一直角坐标系中,函数
和
(
是常数,且
)的图象可能是(
)
典型题型3
二次函数与一次函数的综合
x
y
O
A.
x
y
O
B.
x
y
O
C.
x
y
O
D.
若A(-4,y1),B(-3,y2),C(1,y3)为二次函数y=x2+4x-5的图象上的三点,则y1,y2,y3的大小关系是(
)
A、y1<y2<y3
B、y2<y1<y3
C、y3<y1<y2
D、y1<y3<y2
典型题型2
二次函数函数值大小比较
看到题目里有比大小,涉及到的知识点就是二次函数对称轴
把x的值直接代入解析式
根据图像的对称性,把所有点移到对称轴一边,再比较
两种做题方法
将二次函数y=x2+3x+4向左平移2个单位长度,再向上平移3个单位长度得到的解析式为
典型题型4
二次函数图像的平移
平移规律
左右平移改变x,即含有x的项都要变,左+右-
上下平移改变y,即直接在等式后面加减,上+下-
知识点三:二次函数的解析式求法
1.一般式法:y=ax2+bx+c
(a≠
0)
2.顶点法:y=a(x-h)2+k(a≠0)
3.交点法:y=a(x-x1)(x-x2)(a≠0)
三种解析式的适用条件
已知3个点的坐标,可以用一般式求解析式
已知顶点坐标和其它任意两点坐标,可以用顶点式求解析式
已知与x轴的两个点的坐标以及其它任意一个点的坐标,可用交点式求解析式(也可用一般式)
典型题型
若一抛物线形状与y=-5x2+2相同,顶点坐标是(4,-2),则其解析式是_____________.
已知关于x的二次函数,当x=-1时,函数值为10,当x=1时,函数值为4,当x=2时,函数值为7,则其解析式是_____________.
判别式△=b2-4ac
二次函数y=ax2+bx+c
(a>0)
的图象
一元二次方程ax2+bx+c=0
(a≠0)的根
不等式ax2+bx+c>0(a>0)的解集
不等式ax2+bx+c<0(a>0)的解集
x2
x1
x
y
o
O
x1=
x2
x
y
x
O
x
y
x
△>0
△=0
△<0
x1
;
x2
x1
=x2
=-b/2a
没有实数根
x
x
≠
x1的一切实数
所有实数
x1
无解
知识点四:二次函数与一元二次方程以及
一元二次不等式的关系
二次函数y=kx2-6x+3的图象与x轴有交点,则k的取值范围是( )
A.k<3
B.k<3且k≠0
C.k≤3
D.k≤3且k≠0
典型题型1
如果这题把二次函数中
二次这个前提去掉,
答案还会一样吗?
已知二次函数y=2(x-1)(x-m-3)(m为常数)。
(1)求证:不论m为何值,该函数的图像与x轴总有公共点。
(2)当m取何值时,该函数的图像与y轴的交点在x轴上方?
典型题型2
如图,
某中学要在教学楼后面的空地上用40米长的竹篱笆围出一个矩形地块作生物园,
矩形的一边用教学楼的外墙,其余三边用竹篱笆.
设矩形的宽为x,面积为y.
(1)
求y与x的函数关系式,并求自变量的取值范围;
(2)
生物园的面积能否达到210平方米?说明理由.
知识点五:二次函数的几种常见应用题型
第一类:面积最值问题
教学楼
x
第二类:利润最值问题
小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元,调研发现:
①盆景每增加1盆,盆景的平均每盆利润减少2元;每减少1盆,盆景的平均每盆利润增加2元;②花卉的平均每盆利润始终不变.
小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x盆,第二期盆景与花卉售完后的利润分别为W1,W2(单位:元)
(1)用含x的代数式分别表示W1,W2;
(2)当x取何值时,第二期培植的盆景与花卉售完后获得的总利润W最大,最大总利润是多少?
某学校初三年级的一场篮球比赛中,如图,队员甲正在投篮,已知球出手时距地面
米,与篮框中心的水平距离为7米,当球出手后水平距离为4米时到达最大高度4米,设篮球运行轨迹为抛物线,篮框距地面3米.
(1)建立如图所示的平面直角坐标系,问此球能否准确投中?
第三类:抛物问题
(2)此时,若对方队员乙在甲面前1米处跳起盖帽拦截,已知乙的最大摸高为3.1米,那么他能否获得成功?
A
B
C
今天也是粉色的心情
每天都是喜欢的自己
同课章节目录
