11.4.2平面与平面垂直 同步作业2020-2021学年高一数学人教版B版(2019)必修第四册第十一章(含答案)
文档属性
| 名称 | 11.4.2平面与平面垂直 同步作业2020-2021学年高一数学人教版B版(2019)必修第四册第十一章(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 235.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-31 00:00:00 | ||
图片预览




文档简介
平面与平面垂直
1.对于直线m,n和平面α,β,能得出α⊥β的一个条件是
( )
A.m⊥n,m∥α,n∥β
B.m⊥n,α∩β,n?α
C.m∥n,n⊥β,m?α
D.m∥n,m⊥α,n⊥β
2.如图所示,四边形ABCD是矩形,PA⊥平面ABCD,则图中互相垂直的平面共有
( )
A.3对
B.4对
C.5对
D.6对
3.设m,n是两条不同的直线,α,β是两个不同的平面.下列命题中正确的是
( )
A.若α⊥β,m?α,n?β,则m⊥n
B.若α∥β,m?α,n?β,则m∥n
C.若m⊥n,m?α,n?β,则α⊥β
D.若m⊥α,m∥n,n∥β,则α⊥β
4.矩形ABCD的两边AB=3,AD=4,PA⊥平面ABCD,且PA=,则二面角A-BD-P的度数为
( )
A.30°
B.45°
C.60°
D.120°
5.如图所示,平面α⊥平面β,在α与β交线上取线段AB=4,AC,BD分别在平面α和β内,AC⊥AB,BD⊥AB,AC=3,BD=12,则CD= .?
6.如图所示,已知正方体ABCD-A1B1C1D1中,E为棱CC1上的动点.
(1)求证:A1E⊥BD.
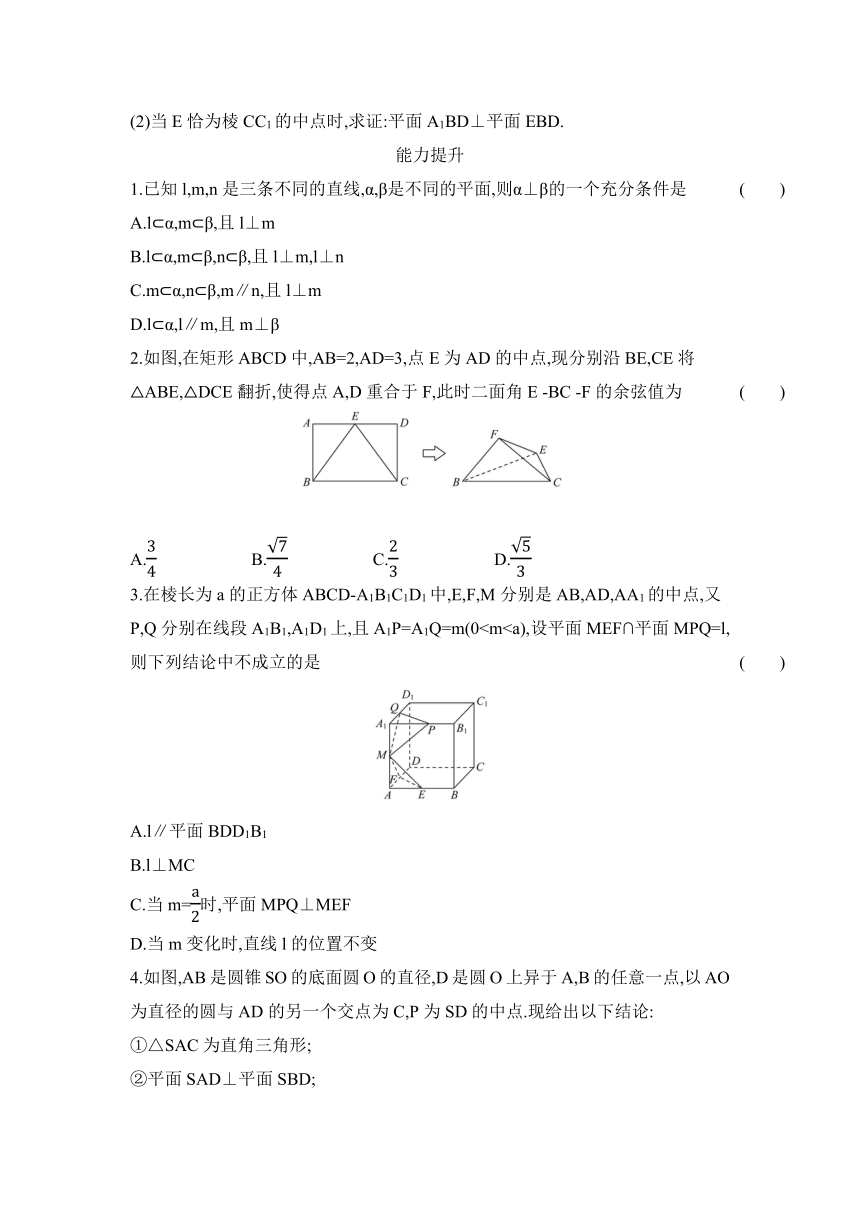
(2)当E恰为棱CC1的中点时,求证:平面A1BD⊥平面EBD.
能力提升
1.已知l,m,n是三条不同的直线,α,β是不同的平面,则α⊥β的一个充分条件是
( )
A.l?α,m?β,且l⊥m
B.l?α,m?β,n?β,且l⊥m,l⊥n
C.m?α,n?β,m∥n,且l⊥m
D.l?α,l∥m,且m⊥β
2.如图,在矩形ABCD中,AB=2,AD=3,点E为AD的中点,现分别沿BE,CE将△ABE,△DCE翻折,使得点A,D重合于F,此时二面角E
-BC
-F的余弦值为
( )
A.
B.
C.
D.
3.在棱长为a的正方体ABCD-A1B1C1D1中,E,F,M分别是AB,AD,AA1的中点,又P,Q分别在线段A1B1,A1D1上,且A1P=A1Q=m(0( )
A.l∥平面BDD1B1
B.l⊥MC
C.当m=时,平面MPQ⊥MEF
D.当m变化时,直线l的位置不变
4.如图,AB是圆锥SO的底面圆O的直径,D是圆O上异于A,B的任意一点,以AO为直径的圆与AD的另一个交点为C,P为SD的中点.现给出以下结论:
①△SAC为直角三角形;
②平面SAD⊥平面SBD;
③平面PAB必与圆锥SO的某条母线平行.
其中正确结论的个数是
( )
A.0
B.1
C.2
D.3
5.已知直线l,m,平面α,β,且l⊥α,m?β,下列四个命题中正确命题是
( )
A.若α∥β,则l⊥m
B.若l⊥m,则α∥β
C.若α⊥β,则l∥m
D.若l∥m,则α⊥β
6.如图所示,已知正方体ABCD-A1B1C1D1,E,F分别是D1B,A1C上不重合的两个动点,下列四个结论中正确的是
( )
A.CE∥D1F
B.平面AFD∥平面B1EC1
C.AB1⊥EF
D.平面AED⊥平面ABB1A1
7.已知正方形ABCD的边长为1,将△ADC沿对角线AC折起,若折叠后平面ACD⊥平面ACB,则此时AC与BD所成角的大小是 ,点B,D之间的距离是 .?
8.如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面各边都相等,M是PC上的一动点,当点M满足条件①BM⊥DM,②DM⊥PC,③BM⊥PC中的 时,平面MBD⊥平面PCD(只要填写一个你认为是正确的条件序号即可).?
9.如图所示,△ABC是正三角形,线段EA和DC都垂直于平面ABC,设EA=AB=2a,DC=a,且F为BE的中点.
(1)求证:DF∥平面ABC.
(2)求证:AF⊥BD.
(3)求平面BDF与平面ABC所成的较小二面角的大小.
10.已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E,F分别是AC,AD上的动点,且==λ(0<λ<1).
(1)求证:不论λ为何值,总有平面BEF⊥平面ABC;
(2)当λ为何值时,平面BEF⊥平面ACD.
参考答案
1.对于直线m,n和平面α,β,能得出α⊥β的一个条件是
( )
A.m⊥n,m∥α,n∥β
B.m⊥n,α∩β,n?α
C.m∥n,n⊥β,m?α
D.m∥n,m⊥α,n⊥β
分析:选C.因为n⊥β,m∥n,所以m⊥β,又m?α,由面面垂直的判定定理,得α⊥β.
2.如图所示,四边形ABCD是矩形,PA⊥平面ABCD,则图中互相垂直的平面共有
( )
A.3对
B.4对
C.5对
D.6对
分析:选D.因为PA⊥平面ABCD,且PA?平面PAB,
PA?平面PAD,PA?平面PAC,
所以平面PAB和平面PAC和平面PAD都与平面ABCD垂直,
又AD⊥PA,AD⊥AB,所以AD⊥平面PAB,
又AD?平面PAD,
所以平面PAB⊥平面PAD,
同理可证平面PBC⊥平面PAB,
平面PCD⊥平面PAD.
3.设m,n是两条不同的直线,α,β是两个不同的平面.下列命题中正确的是
( )
A.若α⊥β,m?α,n?β,则m⊥n
B.若α∥β,m?α,n?β,则m∥n
C.若m⊥n,m?α,n?β,则α⊥β
D.若m⊥α,m∥n,n∥β,则α⊥β
分析:选D.A中,m,n可能为平行、垂直、异面直线;B中,m,n可能为异面直线;C中,m应与β中两条相交直线垂直时结论才成立.
4.矩形ABCD的两边AB=3,AD=4,PA⊥平面ABCD,且PA=,则二面角A-BD-P的度数为
( )
A.30°
B.45°
C.60°
D.120°
分析:选A.过A作AE⊥BD,连接PE,
则∠AEP为所求角.
由AB=3,AD=4知BD=5.
又AB·AD=BD·AE,所以AE=,
所以tan∠AEP==.所以∠AEP=30°.
5.如图所示,平面α⊥平面β,在α与β交线上取线段AB=4,AC,BD分别在平面α和β内,AC⊥AB,BD⊥AB,AC=3,BD=12,则CD= .?
分析:连接BC.因为BD⊥AB,α⊥β,α∩β=AB,
所以BD⊥α.因为BC?α,
所以BD⊥BC,
所以△CBD是直角三角形.
在Rt△BAC中,BC==5.
在Rt△CBD中,CD==13.
答案:13
6.如图所示,已知正方体ABCD-A1B1C1D1中,E为棱CC1上的动点.
(1)求证:A1E⊥BD.
(2)当E恰为棱CC1的中点时,求证:平面A1BD⊥平面EBD.
【证明】连接AC,设AC∩DB=O,连接A1O,OE,
(1)因为AA1⊥底面ABCD,所以BD⊥A1A,
又BD⊥AC,A1A∩AC=A,所以BD⊥平面ACEA1,
因为A1E?平面ACEA1,所以A1E⊥BD.
(2)在等边三角形A1BD中,BD⊥A1O,
因为BD⊥平面ACEA1,OE?平面ACEA1,
所以BD⊥OE,所以∠A1OE为二面角A1-BD-E的平面角.
在正方体ABCD-A1B1C1D1中,设棱长为2a,
因为E为棱CC1的中点,由平面几何知识,
得EO=a,A1O=a,A1E=3a,
满足A1E2=A1O2+EO2,所以∠A1OE=90°,
即平面A1BD⊥平面EBD.
能力提升
1.已知l,m,n是三条不同的直线,α,β是不同的平面,则α⊥β的一个充分条件是
( )
A.l?α,m?β,且l⊥m
B.l?α,m?β,n?β,且l⊥m,l⊥n
C.m?α,n?β,m∥n,且l⊥m
D.l?α,l∥m,且m⊥β
分析:选D.A选项,l?α,m?β,且l⊥m,
如图1,α,β不垂直;B选项,l?α,m?β,n?β,且l⊥m,l⊥n,
如图2,α,β不垂直;
C选项,m?α,n?β,m∥n,且l⊥m,直线l没有确定,则α,β的关系也不能确定;D选项,l?α,l∥m,且m⊥β,则必有l⊥β,根据面面垂直的判定定理知,
α⊥β.
2.如图,在矩形ABCD中,AB=2,AD=3,点E为AD的中点,现分别沿BE,CE将△ABE,△DCE翻折,使得点A,D重合于F,此时二面角E
-BC
-F的余弦值为
( )
A.
B.
C.
D.
分析:选B.取BC的中点O,连接OE,OF,
因为BA=CD,所以BF=FC,即三角形BFC是等腰三角形,
则FO⊥BC,因为BE=CE,
所以△BEC是等腰三角形,所以EO⊥BC,
则∠FOE是二面角E
-BC
-F的平面角,
因为EF⊥CF,BF⊥EF,
所以EF⊥平面BCF,EF⊥FO,
则直角三角形EFO中,OE=AB=2,EF=DE=,
所以OF===,
则cos∠FOE===.
3.在棱长为a的正方体ABCD-A1B1C1D1中,E,F,M分别是AB,AD,AA1的中点,又P,Q分别在线段A1B1,A1D1上,且A1P=A1Q=m(0( )
A.l∥平面BDD1B1
B.l⊥MC
C.当m=时,平面MPQ⊥MEF
D.当m变化时,直线l的位置不变
分析:选C.因为A1P=A1Q=m,
所以PQ∥B1D1,因为E,F分别是AB,AD的中点,
所以EF∥BD,
所以PQ∥EF,
因为平面MEF∩平面MPQ=l,
所以PQ∥EF∥l.选项A,D显然成立;
因为BD∥EF∥l,BD⊥平面ACC1A1,
所以l⊥平面ACC1A1,
因为MC?平面ACC1A1,
所以l⊥MC,所以B选项成立;
易知AC1⊥平面MEF,A1C⊥平面MPQ,而直线AC1与A1C不垂直,所以C项不成立.
4.如图,AB是圆锥SO的底面圆O的直径,D是圆O上异于A,B的任意一点,以AO为直径的圆与AD的另一个交点为C,P为SD的中点.现给出以下结论:
①△SAC为直角三角形;
②平面SAD⊥平面SBD;
③平面PAB必与圆锥SO的某条母线平行.
其中正确结论的个数是
( )
A.0
B.1
C.2
D.3
分析:选C.①因为SO⊥底面圆O,
所以SO⊥AC,C在以AO为直径的圆上,
所以AC⊥OC,因为OC∩SO=O,
所以AC⊥平面SOC,AC⊥SC,
即△SAC为直角三角形,故①正确;
②假设平面SAD⊥平面SBD,在平面SAD中过A作AH⊥SD交SD于H,
则AH⊥平面SBD,所以AH⊥BD,
又因为BD⊥AD,
所以BD⊥平面SAD,又CO∥BD,
所以CO⊥平面SAD,所以CO⊥SC,
又在△SOC中,SO⊥OC,在一个三角形内不可能有两个直角,故平面SAD⊥平面SBD不成立,故②错误;
③连接DO并延长交圆于E,连接PO,SE,
因为P为SD的中点,O为ED的中点,
所以OP是△SDE的中位线,
所以PO∥SE,即SE∥平面APB,
即平面PAB必与圆锥SO的母线SE平行,故③正确.故正确的是①③.
5.已知直线l,m,平面α,β,且l⊥α,m?β,下列四个命题中正确命题是
( )
A.若α∥β,则l⊥m
B.若l⊥m,则α∥β
C.若α⊥β,则l∥m
D.若l∥m,则α⊥β
分析:选AD.A选项,若α∥β,
因为l⊥α,则l⊥β,又因为m?β,所以l⊥m.故A正确;
B选项,举反例,当α∩β=m时,满足l⊥α,m?β,l⊥m,故B错;
C选项,举反例,当α∩β=m时,满足l⊥α,m?β,α⊥β,
则l⊥m,故C错;D选项,若l∥m,
则m⊥α,因为m?β,所以α⊥β,D正确.
6.如图所示,已知正方体ABCD-A1B1C1D1,E,F分别是D1B,A1C上不重合的两个动点,下列四个结论中正确的是
( )
A.CE∥D1F
B.平面AFD∥平面B1EC1
C.AB1⊥EF
D.平面AED⊥平面ABB1A1
分析:选CD.A选项,如图,
在D1B,A1C上分别取点E,F,
因为ABCD-A1B1C1D1为正方体,
则四边形A1BCD1为矩形,因为∠FD1C+∠ECD1<∠A1D1C+∠BCD1=180°,
所以CE与D1F不平行,故A错误;B选项,不妨取F与A1重合,E与O重合,此时平面AFD与平面B1EC1相交,故B错误;C选项,AB1⊥A1B,AB1⊥BC,且A1B∩BC=B,则AB1⊥平面A1BCD1,则AB1⊥EF,故C正确;D选项,AD⊥平面ABB1A1,而AD?平面AED,则平面AED⊥平面ABB1A1,故D正确.
7.已知正方形ABCD的边长为1,将△ADC沿对角线AC折起,若折叠后平面ACD⊥平面ACB,则此时AC与BD所成角的大小是 ,点B,D之间的距离是 .?
分析:如图所示,取AC的中点O,连接OB,OD.
因为DA=DC,BA=BC,O为AC的中点,
所以DO⊥AC,BO⊥AC,又DO∩BO=O,
所以AC⊥平面BOD,又BD?平面BOD,
所以AC⊥BD,即此时AC与BD所成的角是90°.
因为平面ACD⊥平面ACB,平面ACD∩平面ACB=AC,DO⊥AC,所以DO⊥平面ABC,
所以DO⊥OB,又OB=OD=AC=,
所以BD==1.
答案:90° 1
8.如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面各边都相等,M是PC上的一动点,当点M满足条件①BM⊥DM,②DM⊥PC,③BM⊥PC中的 时,平面MBD⊥平面PCD(只要填写一个你认为是正确的条件序号即可).?
分析:因为PA⊥底面ABCD,所以PA⊥BD,
因为底面各边都相等,所以AC⊥BD,
因为PA∩AC=A,所以BD⊥平面PAC,
所以BD⊥PC,所以当DM⊥PC(或BM⊥PC)时,即有PC⊥平面MBD,而PC?平面PCD,
所以平面MBD⊥平面PCD.
答案:②(或③)
9.如图所示,△ABC是正三角形,线段EA和DC都垂直于平面ABC,设EA=AB=2a,DC=a,且F为BE的中点.
(1)求证:DF∥平面ABC.
(2)求证:AF⊥BD.
(3)求平面BDF与平面ABC所成的较小二面角的大小.
分析:(1)如图所示,取AB中点G,连接CG,FG.
因为EF=FB,AG=GB,所以FG∥EA,
且FG=EA,
又DC∥EA,且DC=EA,
所以FG∥DC,且FG=DC,
所以四边形CDFG为平行四边形,所以DF∥CG,
因为DF?平面ABC,CG?平面ABC,
所以DF∥平面ABC.
(2)因为
EA⊥平面ABC,所以EA⊥CG.
又△ABC
是正三角形,G是AB的中点,
所以CG⊥AB.
又EA∩AB=A,所以CG⊥平面AEB.
又因为DF∥CG,所以DF⊥平面AEB.
所以DF⊥AF.
因为AE=AB,EF=FB,
所以AF⊥BE,又BE∩DF=F,
所以AF⊥平面BED,
所以AF⊥BD.
(3)延长ED交AC延长线于G′,连接BG′.
由DC∥EA,且DC=EA知,D为EG′的中点,
所以FD∥BG′.又CG⊥平面ABE,
FD∥CG,
所以BG′⊥平面ABE.
所以∠EBA为所求二面角的平面角.
在等腰直角三角形AEB中,可得∠EBA=45°.
所以平面BDE与平面ABC所成的较小二面角是45°.
10.已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E,F分别是AC,AD上的动点,且==λ(0<λ<1).
(1)求证:不论λ为何值,总有平面BEF⊥平面ABC;
(2)当λ为何值时,平面BEF⊥平面ACD.
分析:
(1)因为AB⊥平面BCD,
所以AB⊥CD.因为CD⊥BC,且AB∩BC=B,
所以CD⊥平面ABC.又==λ(0<λ<1),
所以不论λ为何值,恒有EF∥CD,
所以EF⊥平面ABC,又EF?平面BEF,
所以不论λ为何值,恒有平面BEF⊥平面ABC.
(2)由(1)知,EF⊥BE,又平面BEF⊥平面ACD,
所以BE⊥平面ACD,所以BE⊥AC.
因为BC=CD=1,∠BCD=90°,∠ADB=60°,
AB⊥平面BCD,所以BD=,AB=tan
60°=,
所以AC==,
由AB2=AE·AC得AE=,
所以λ==,故当λ=时,平面BEF⊥平面ACD.
1.对于直线m,n和平面α,β,能得出α⊥β的一个条件是
( )
A.m⊥n,m∥α,n∥β
B.m⊥n,α∩β,n?α
C.m∥n,n⊥β,m?α
D.m∥n,m⊥α,n⊥β
2.如图所示,四边形ABCD是矩形,PA⊥平面ABCD,则图中互相垂直的平面共有
( )
A.3对
B.4对
C.5对
D.6对
3.设m,n是两条不同的直线,α,β是两个不同的平面.下列命题中正确的是
( )
A.若α⊥β,m?α,n?β,则m⊥n
B.若α∥β,m?α,n?β,则m∥n
C.若m⊥n,m?α,n?β,则α⊥β
D.若m⊥α,m∥n,n∥β,则α⊥β
4.矩形ABCD的两边AB=3,AD=4,PA⊥平面ABCD,且PA=,则二面角A-BD-P的度数为
( )
A.30°
B.45°
C.60°
D.120°
5.如图所示,平面α⊥平面β,在α与β交线上取线段AB=4,AC,BD分别在平面α和β内,AC⊥AB,BD⊥AB,AC=3,BD=12,则CD= .?
6.如图所示,已知正方体ABCD-A1B1C1D1中,E为棱CC1上的动点.
(1)求证:A1E⊥BD.
(2)当E恰为棱CC1的中点时,求证:平面A1BD⊥平面EBD.
能力提升
1.已知l,m,n是三条不同的直线,α,β是不同的平面,则α⊥β的一个充分条件是
( )
A.l?α,m?β,且l⊥m
B.l?α,m?β,n?β,且l⊥m,l⊥n
C.m?α,n?β,m∥n,且l⊥m
D.l?α,l∥m,且m⊥β
2.如图,在矩形ABCD中,AB=2,AD=3,点E为AD的中点,现分别沿BE,CE将△ABE,△DCE翻折,使得点A,D重合于F,此时二面角E
-BC
-F的余弦值为
( )
A.
B.
C.
D.
3.在棱长为a的正方体ABCD-A1B1C1D1中,E,F,M分别是AB,AD,AA1的中点,又P,Q分别在线段A1B1,A1D1上,且A1P=A1Q=m(0
A.l∥平面BDD1B1
B.l⊥MC
C.当m=时,平面MPQ⊥MEF
D.当m变化时,直线l的位置不变
4.如图,AB是圆锥SO的底面圆O的直径,D是圆O上异于A,B的任意一点,以AO为直径的圆与AD的另一个交点为C,P为SD的中点.现给出以下结论:
①△SAC为直角三角形;
②平面SAD⊥平面SBD;
③平面PAB必与圆锥SO的某条母线平行.
其中正确结论的个数是
( )
A.0
B.1
C.2
D.3
5.已知直线l,m,平面α,β,且l⊥α,m?β,下列四个命题中正确命题是
( )
A.若α∥β,则l⊥m
B.若l⊥m,则α∥β
C.若α⊥β,则l∥m
D.若l∥m,则α⊥β
6.如图所示,已知正方体ABCD-A1B1C1D1,E,F分别是D1B,A1C上不重合的两个动点,下列四个结论中正确的是
( )
A.CE∥D1F
B.平面AFD∥平面B1EC1
C.AB1⊥EF
D.平面AED⊥平面ABB1A1
7.已知正方形ABCD的边长为1,将△ADC沿对角线AC折起,若折叠后平面ACD⊥平面ACB,则此时AC与BD所成角的大小是 ,点B,D之间的距离是 .?
8.如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面各边都相等,M是PC上的一动点,当点M满足条件①BM⊥DM,②DM⊥PC,③BM⊥PC中的 时,平面MBD⊥平面PCD(只要填写一个你认为是正确的条件序号即可).?
9.如图所示,△ABC是正三角形,线段EA和DC都垂直于平面ABC,设EA=AB=2a,DC=a,且F为BE的中点.
(1)求证:DF∥平面ABC.
(2)求证:AF⊥BD.
(3)求平面BDF与平面ABC所成的较小二面角的大小.
10.已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E,F分别是AC,AD上的动点,且==λ(0<λ<1).
(1)求证:不论λ为何值,总有平面BEF⊥平面ABC;
(2)当λ为何值时,平面BEF⊥平面ACD.
参考答案
1.对于直线m,n和平面α,β,能得出α⊥β的一个条件是
( )
A.m⊥n,m∥α,n∥β
B.m⊥n,α∩β,n?α
C.m∥n,n⊥β,m?α
D.m∥n,m⊥α,n⊥β
分析:选C.因为n⊥β,m∥n,所以m⊥β,又m?α,由面面垂直的判定定理,得α⊥β.
2.如图所示,四边形ABCD是矩形,PA⊥平面ABCD,则图中互相垂直的平面共有
( )
A.3对
B.4对
C.5对
D.6对
分析:选D.因为PA⊥平面ABCD,且PA?平面PAB,
PA?平面PAD,PA?平面PAC,
所以平面PAB和平面PAC和平面PAD都与平面ABCD垂直,
又AD⊥PA,AD⊥AB,所以AD⊥平面PAB,
又AD?平面PAD,
所以平面PAB⊥平面PAD,
同理可证平面PBC⊥平面PAB,
平面PCD⊥平面PAD.
3.设m,n是两条不同的直线,α,β是两个不同的平面.下列命题中正确的是
( )
A.若α⊥β,m?α,n?β,则m⊥n
B.若α∥β,m?α,n?β,则m∥n
C.若m⊥n,m?α,n?β,则α⊥β
D.若m⊥α,m∥n,n∥β,则α⊥β
分析:选D.A中,m,n可能为平行、垂直、异面直线;B中,m,n可能为异面直线;C中,m应与β中两条相交直线垂直时结论才成立.
4.矩形ABCD的两边AB=3,AD=4,PA⊥平面ABCD,且PA=,则二面角A-BD-P的度数为
( )
A.30°
B.45°
C.60°
D.120°
分析:选A.过A作AE⊥BD,连接PE,
则∠AEP为所求角.
由AB=3,AD=4知BD=5.
又AB·AD=BD·AE,所以AE=,
所以tan∠AEP==.所以∠AEP=30°.
5.如图所示,平面α⊥平面β,在α与β交线上取线段AB=4,AC,BD分别在平面α和β内,AC⊥AB,BD⊥AB,AC=3,BD=12,则CD= .?
分析:连接BC.因为BD⊥AB,α⊥β,α∩β=AB,
所以BD⊥α.因为BC?α,
所以BD⊥BC,
所以△CBD是直角三角形.
在Rt△BAC中,BC==5.
在Rt△CBD中,CD==13.
答案:13
6.如图所示,已知正方体ABCD-A1B1C1D1中,E为棱CC1上的动点.
(1)求证:A1E⊥BD.
(2)当E恰为棱CC1的中点时,求证:平面A1BD⊥平面EBD.
【证明】连接AC,设AC∩DB=O,连接A1O,OE,
(1)因为AA1⊥底面ABCD,所以BD⊥A1A,
又BD⊥AC,A1A∩AC=A,所以BD⊥平面ACEA1,
因为A1E?平面ACEA1,所以A1E⊥BD.
(2)在等边三角形A1BD中,BD⊥A1O,
因为BD⊥平面ACEA1,OE?平面ACEA1,
所以BD⊥OE,所以∠A1OE为二面角A1-BD-E的平面角.
在正方体ABCD-A1B1C1D1中,设棱长为2a,
因为E为棱CC1的中点,由平面几何知识,
得EO=a,A1O=a,A1E=3a,
满足A1E2=A1O2+EO2,所以∠A1OE=90°,
即平面A1BD⊥平面EBD.
能力提升
1.已知l,m,n是三条不同的直线,α,β是不同的平面,则α⊥β的一个充分条件是
( )
A.l?α,m?β,且l⊥m
B.l?α,m?β,n?β,且l⊥m,l⊥n
C.m?α,n?β,m∥n,且l⊥m
D.l?α,l∥m,且m⊥β
分析:选D.A选项,l?α,m?β,且l⊥m,
如图1,α,β不垂直;B选项,l?α,m?β,n?β,且l⊥m,l⊥n,
如图2,α,β不垂直;
C选项,m?α,n?β,m∥n,且l⊥m,直线l没有确定,则α,β的关系也不能确定;D选项,l?α,l∥m,且m⊥β,则必有l⊥β,根据面面垂直的判定定理知,
α⊥β.
2.如图,在矩形ABCD中,AB=2,AD=3,点E为AD的中点,现分别沿BE,CE将△ABE,△DCE翻折,使得点A,D重合于F,此时二面角E
-BC
-F的余弦值为
( )
A.
B.
C.
D.
分析:选B.取BC的中点O,连接OE,OF,
因为BA=CD,所以BF=FC,即三角形BFC是等腰三角形,
则FO⊥BC,因为BE=CE,
所以△BEC是等腰三角形,所以EO⊥BC,
则∠FOE是二面角E
-BC
-F的平面角,
因为EF⊥CF,BF⊥EF,
所以EF⊥平面BCF,EF⊥FO,
则直角三角形EFO中,OE=AB=2,EF=DE=,
所以OF===,
则cos∠FOE===.
3.在棱长为a的正方体ABCD-A1B1C1D1中,E,F,M分别是AB,AD,AA1的中点,又P,Q分别在线段A1B1,A1D1上,且A1P=A1Q=m(0
A.l∥平面BDD1B1
B.l⊥MC
C.当m=时,平面MPQ⊥MEF
D.当m变化时,直线l的位置不变
分析:选C.因为A1P=A1Q=m,
所以PQ∥B1D1,因为E,F分别是AB,AD的中点,
所以EF∥BD,
所以PQ∥EF,
因为平面MEF∩平面MPQ=l,
所以PQ∥EF∥l.选项A,D显然成立;
因为BD∥EF∥l,BD⊥平面ACC1A1,
所以l⊥平面ACC1A1,
因为MC?平面ACC1A1,
所以l⊥MC,所以B选项成立;
易知AC1⊥平面MEF,A1C⊥平面MPQ,而直线AC1与A1C不垂直,所以C项不成立.
4.如图,AB是圆锥SO的底面圆O的直径,D是圆O上异于A,B的任意一点,以AO为直径的圆与AD的另一个交点为C,P为SD的中点.现给出以下结论:
①△SAC为直角三角形;
②平面SAD⊥平面SBD;
③平面PAB必与圆锥SO的某条母线平行.
其中正确结论的个数是
( )
A.0
B.1
C.2
D.3
分析:选C.①因为SO⊥底面圆O,
所以SO⊥AC,C在以AO为直径的圆上,
所以AC⊥OC,因为OC∩SO=O,
所以AC⊥平面SOC,AC⊥SC,
即△SAC为直角三角形,故①正确;
②假设平面SAD⊥平面SBD,在平面SAD中过A作AH⊥SD交SD于H,
则AH⊥平面SBD,所以AH⊥BD,
又因为BD⊥AD,
所以BD⊥平面SAD,又CO∥BD,
所以CO⊥平面SAD,所以CO⊥SC,
又在△SOC中,SO⊥OC,在一个三角形内不可能有两个直角,故平面SAD⊥平面SBD不成立,故②错误;
③连接DO并延长交圆于E,连接PO,SE,
因为P为SD的中点,O为ED的中点,
所以OP是△SDE的中位线,
所以PO∥SE,即SE∥平面APB,
即平面PAB必与圆锥SO的母线SE平行,故③正确.故正确的是①③.
5.已知直线l,m,平面α,β,且l⊥α,m?β,下列四个命题中正确命题是
( )
A.若α∥β,则l⊥m
B.若l⊥m,则α∥β
C.若α⊥β,则l∥m
D.若l∥m,则α⊥β
分析:选AD.A选项,若α∥β,
因为l⊥α,则l⊥β,又因为m?β,所以l⊥m.故A正确;
B选项,举反例,当α∩β=m时,满足l⊥α,m?β,l⊥m,故B错;
C选项,举反例,当α∩β=m时,满足l⊥α,m?β,α⊥β,
则l⊥m,故C错;D选项,若l∥m,
则m⊥α,因为m?β,所以α⊥β,D正确.
6.如图所示,已知正方体ABCD-A1B1C1D1,E,F分别是D1B,A1C上不重合的两个动点,下列四个结论中正确的是
( )
A.CE∥D1F
B.平面AFD∥平面B1EC1
C.AB1⊥EF
D.平面AED⊥平面ABB1A1
分析:选CD.A选项,如图,
在D1B,A1C上分别取点E,F,
因为ABCD-A1B1C1D1为正方体,
则四边形A1BCD1为矩形,因为∠FD1C+∠ECD1<∠A1D1C+∠BCD1=180°,
所以CE与D1F不平行,故A错误;B选项,不妨取F与A1重合,E与O重合,此时平面AFD与平面B1EC1相交,故B错误;C选项,AB1⊥A1B,AB1⊥BC,且A1B∩BC=B,则AB1⊥平面A1BCD1,则AB1⊥EF,故C正确;D选项,AD⊥平面ABB1A1,而AD?平面AED,则平面AED⊥平面ABB1A1,故D正确.
7.已知正方形ABCD的边长为1,将△ADC沿对角线AC折起,若折叠后平面ACD⊥平面ACB,则此时AC与BD所成角的大小是 ,点B,D之间的距离是 .?
分析:如图所示,取AC的中点O,连接OB,OD.
因为DA=DC,BA=BC,O为AC的中点,
所以DO⊥AC,BO⊥AC,又DO∩BO=O,
所以AC⊥平面BOD,又BD?平面BOD,
所以AC⊥BD,即此时AC与BD所成的角是90°.
因为平面ACD⊥平面ACB,平面ACD∩平面ACB=AC,DO⊥AC,所以DO⊥平面ABC,
所以DO⊥OB,又OB=OD=AC=,
所以BD==1.
答案:90° 1
8.如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面各边都相等,M是PC上的一动点,当点M满足条件①BM⊥DM,②DM⊥PC,③BM⊥PC中的 时,平面MBD⊥平面PCD(只要填写一个你认为是正确的条件序号即可).?
分析:因为PA⊥底面ABCD,所以PA⊥BD,
因为底面各边都相等,所以AC⊥BD,
因为PA∩AC=A,所以BD⊥平面PAC,
所以BD⊥PC,所以当DM⊥PC(或BM⊥PC)时,即有PC⊥平面MBD,而PC?平面PCD,
所以平面MBD⊥平面PCD.
答案:②(或③)
9.如图所示,△ABC是正三角形,线段EA和DC都垂直于平面ABC,设EA=AB=2a,DC=a,且F为BE的中点.
(1)求证:DF∥平面ABC.
(2)求证:AF⊥BD.
(3)求平面BDF与平面ABC所成的较小二面角的大小.
分析:(1)如图所示,取AB中点G,连接CG,FG.
因为EF=FB,AG=GB,所以FG∥EA,
且FG=EA,
又DC∥EA,且DC=EA,
所以FG∥DC,且FG=DC,
所以四边形CDFG为平行四边形,所以DF∥CG,
因为DF?平面ABC,CG?平面ABC,
所以DF∥平面ABC.
(2)因为
EA⊥平面ABC,所以EA⊥CG.
又△ABC
是正三角形,G是AB的中点,
所以CG⊥AB.
又EA∩AB=A,所以CG⊥平面AEB.
又因为DF∥CG,所以DF⊥平面AEB.
所以DF⊥AF.
因为AE=AB,EF=FB,
所以AF⊥BE,又BE∩DF=F,
所以AF⊥平面BED,
所以AF⊥BD.
(3)延长ED交AC延长线于G′,连接BG′.
由DC∥EA,且DC=EA知,D为EG′的中点,
所以FD∥BG′.又CG⊥平面ABE,
FD∥CG,
所以BG′⊥平面ABE.
所以∠EBA为所求二面角的平面角.
在等腰直角三角形AEB中,可得∠EBA=45°.
所以平面BDE与平面ABC所成的较小二面角是45°.
10.已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E,F分别是AC,AD上的动点,且==λ(0<λ<1).
(1)求证:不论λ为何值,总有平面BEF⊥平面ABC;
(2)当λ为何值时,平面BEF⊥平面ACD.
分析:
(1)因为AB⊥平面BCD,
所以AB⊥CD.因为CD⊥BC,且AB∩BC=B,
所以CD⊥平面ABC.又==λ(0<λ<1),
所以不论λ为何值,恒有EF∥CD,
所以EF⊥平面ABC,又EF?平面BEF,
所以不论λ为何值,恒有平面BEF⊥平面ABC.
(2)由(1)知,EF⊥BE,又平面BEF⊥平面ACD,
所以BE⊥平面ACD,所以BE⊥AC.
因为BC=CD=1,∠BCD=90°,∠ADB=60°,
AB⊥平面BCD,所以BD=,AB=tan
60°=,
所以AC==,
由AB2=AE·AC得AE=,
所以λ==,故当λ=时,平面BEF⊥平面ACD.
