华师大版数学九年级上册 23.3.2相似三角形的判定(一) 课件(共21张PPT)
文档属性
| 名称 | 华师大版数学九年级上册 23.3.2相似三角形的判定(一) 课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 848.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-31 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
A
B
C
B′
C′
A′
学习目标:
2.
培养观察、发现、比较、归纳能力,感受两个三角形相似的判定定理与全等三角形判定方法(AAS、ASA)的区别与联系,体验事物间特殊与一般的关系
。
学习目标:
1.探究相似三角形的判定定理一,并能运用其证明两三角形相似.
一、知识回顾
2
、相似三角形的定义是什么?
满足两个条件(1)三边对应成比例(2)三角对应相等的两个三角形是相似三角形.
1
、判定两个三角形全等有哪些定理?
SAS、
ASA、
AAS
、SSS,对于判定直角三角形全等还有HL。
3、平行定理(相似三角形判定的预备定理),并结合图形用字母表示出该定理。
DE∥BC
△ADE∽ABC
D
E
A
B
C
C
A
B
D
E
平行于三角形一边的直线,和其它两边(或两边的延长线)相交所构成的三角形与原三角形相似。
∵
∴
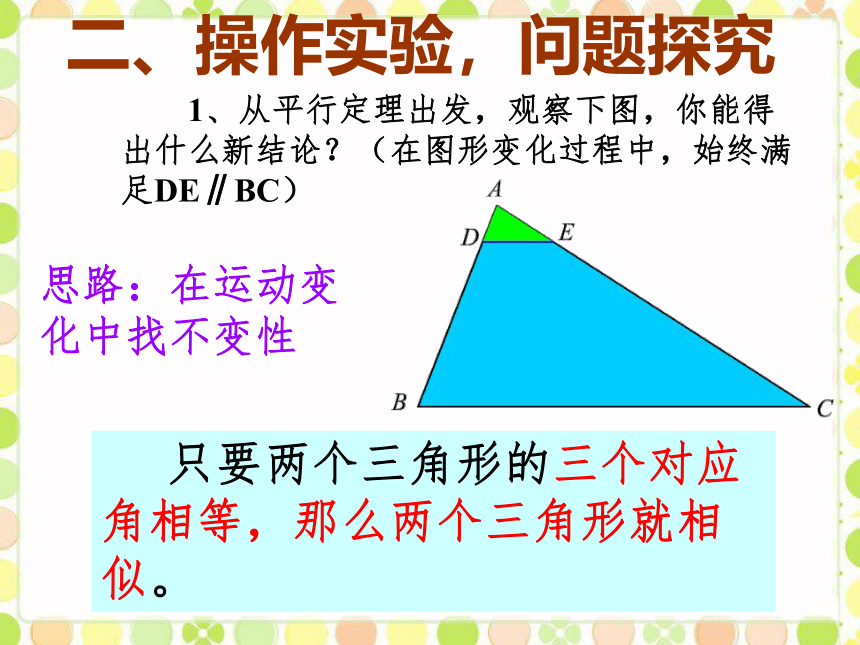
1、从平行定理出发,观察下图,你能得出什么新结论?(在图形变化过程中,始终满足DE∥BC)
在图形运动中,由于DE∥BC,因此在D、E的变化过程中,△ADE的边长在变,而角的大小始终不变。你能大胆猜测出什么结论?
只要两个三角形的三个对应角相等,那么两个三角形就相似。
思路:在运动变化中找不变性
二、操作实验,问题探究
2、动手实践
⑴画一个△ABC,使得∠BAC=60?,
与同桌交流一下,你们所画的三角形相似吗?
有一个角对应相等的两个三角形不一定相似。
⑵与同桌合作:一人画一个△ABC,另一人画△A1B1C1,使得∠A=∠A1=45?,
∠B=∠B1=30?,比较你们画的两个三角形,∠C与∠C1相等吗?对应边的比相等吗?这样的两个三角形相似吗?根据是什么?你猜想出怎样的结论?
∠C=∠C1,对应边的比相等。根据是相似三角形的定义。
三、抽象概括,推理论证
由此我们可猜想到:判定两个三角形相似可以像判定两个三角形全等一样,用较少的条件就能判定。即
如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。
问题:对于一个命题,你准备怎么去说明它的正确性?
论证
已知:在△ABC和△A′B′C中.∠A=∠A′
∠
B=∠B′
求证:△ABC∽△A′B′C′
分析:
A
B
C
A'
C'
B'
要证两个三角形相似,目前只有两个途径。一是三角形相似的定义,(条件较多,不常用);二是平行定理。
D
E
1
为了使用它,就必须创造具备定理的基本图形的
条件。怎样创造呢?
规范推理
D
E
A′
B′
C′
A
B
C
在△ABC的边AB上截取
AD=A’
B’
,过点D作DE∥BC,
交AC于点E.则
△ADE∽△ABC
∴∠ADE=∠B
∵
∠B=∠B’
∴∠ADE=∠B’
又∵
AD=A’B’∠
A=∠A’
∴△ADE≌△A’B’C’
(ASA)
∴△
A’B’C’
∽△ABC
证明:
我们可以得到:相似三角形的判定定理1
如果一个三角形的两个角分别与另一个三角形的两个角对应相等.那么这两个三角形相似.
可简单说成:两个角对应相等的两个三角形相似
得出新知
A
B
C
A'
C'
B'
∠A=∠A′
∠
B=∠B′
△ABC∽△
A’B’C’
符号语言表示为:
∵
∴
想一想:
1、△ABC和△A′B′C′中∠A=80°、∠B=40°、∠A′=80°、∠C′=60°.那么这两个三角形相似吗?
2、等边三角形都相似吗?
3、一个锐角对应相等的两个直角三角形相似吗?
4、各有一内角为400的两个等腰三角形相似吗?
5、各一个内角为
100°的两个等腰三角形相似吗?
四、辨析应用,方法提炼
例.
如图,△ABC中,
DE∥BC,EF∥AB,
试说明△ADE∽△EFC.
A
E
F
B
C
D
解:
∵
DE∥BC,EF∥AB(已知),
∴
∠ADE=∠B=∠EFC
(两直线平行,同位角相等)
∠AED=∠C.
(两直线平行,同位角相等)
∴
△ADE∽△EFC.
(两个角分别对应相等的两个三角形相似.)
A
B
D
C
图
3
填一填
(1)如图3,点D在AB上,当
=
时,
△ACD∽△ABC。
(2)如图4,已知点E在AC上,若点D在AB上,则满足条件
,就可以使△ADE与原△ABC相似。
●
A
B
C
E
图
4
∠
ACD
∠B
(或者∠
ACB=∠
ADB)
DE//BC
D
(或者∠
C=∠
ADE)
(或者∠
B=∠
ADE)
D
例、在四边形ABCD中,AC平分∠DAB,∠ACD=∠ABC。求证:AC2=AB·AD
A
B
C
D
即:AC2=AB·AD
A
B
C
D
E
例.已知D、E分别是△ABC的边AB,AC上的点,若∠A=35°,
∠C=85°,∠AED=60
°则AD·AB=
AE·AC
85°
35°
60°
85°
即:AD·AB=
AE·AC
如图,C是线段BD上的一点,AB⊥BD.ED⊥BD.AC⊥EC。求证:△ABC∽△CDE
E
A
1
B
C
D
2
证明:
∵AB⊥BDED⊥BD
∴∠ABC=∠CDE=90°
∴∠1+∠A=90°
∵AC⊥EC
∴∠1+∠2=90°
∴∠A=∠2
∴△ABC∽△CDE
例题赏析
1、已知:在△ABC∽△A1B1C1,
△A1B1C1∽△A2B2C2
,那么△ABC与△A2B2C2有什么关系,为什么?
证明:∵
△ABC∽△A1B1C1
∴∠A=
∠A1,∠B=
∠B1
∵
△A1B1C1∽△A2B2C2
∴∠A1=
∠A2,∠B1=
∠B2
∴∠A=
∠A2,∠B=
∠B2
∵
△ABC∽△A2B2C2
三角形相似的传递性
练一练:
七、巩固新知
2、写出图中的相似三角形:
(1)条件:
DE∥BC
EF∥AB
(2)条件
∠A=36°
AB=AC
BD平分∠ABC
△ADE∽△ABC∽△EFC
△ABC∽△BDC
A
B
C
D
E
F
A
B
C
D
36°
五、反思总结,知识梳理
回顾一下我们这节课学习了哪些主要知识?
1、相似三角形的判定定理1;
2、思想方法:类比、转化、分类讨论
A
B
C
B′
C′
A′
学习目标:
2.
培养观察、发现、比较、归纳能力,感受两个三角形相似的判定定理与全等三角形判定方法(AAS、ASA)的区别与联系,体验事物间特殊与一般的关系
。
学习目标:
1.探究相似三角形的判定定理一,并能运用其证明两三角形相似.
一、知识回顾
2
、相似三角形的定义是什么?
满足两个条件(1)三边对应成比例(2)三角对应相等的两个三角形是相似三角形.
1
、判定两个三角形全等有哪些定理?
SAS、
ASA、
AAS
、SSS,对于判定直角三角形全等还有HL。
3、平行定理(相似三角形判定的预备定理),并结合图形用字母表示出该定理。
DE∥BC
△ADE∽ABC
D
E
A
B
C
C
A
B
D
E
平行于三角形一边的直线,和其它两边(或两边的延长线)相交所构成的三角形与原三角形相似。
∵
∴
1、从平行定理出发,观察下图,你能得出什么新结论?(在图形变化过程中,始终满足DE∥BC)
在图形运动中,由于DE∥BC,因此在D、E的变化过程中,△ADE的边长在变,而角的大小始终不变。你能大胆猜测出什么结论?
只要两个三角形的三个对应角相等,那么两个三角形就相似。
思路:在运动变化中找不变性
二、操作实验,问题探究
2、动手实践
⑴画一个△ABC,使得∠BAC=60?,
与同桌交流一下,你们所画的三角形相似吗?
有一个角对应相等的两个三角形不一定相似。
⑵与同桌合作:一人画一个△ABC,另一人画△A1B1C1,使得∠A=∠A1=45?,
∠B=∠B1=30?,比较你们画的两个三角形,∠C与∠C1相等吗?对应边的比相等吗?这样的两个三角形相似吗?根据是什么?你猜想出怎样的结论?
∠C=∠C1,对应边的比相等。根据是相似三角形的定义。
三、抽象概括,推理论证
由此我们可猜想到:判定两个三角形相似可以像判定两个三角形全等一样,用较少的条件就能判定。即
如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。
问题:对于一个命题,你准备怎么去说明它的正确性?
论证
已知:在△ABC和△A′B′C中.∠A=∠A′
∠
B=∠B′
求证:△ABC∽△A′B′C′
分析:
A
B
C
A'
C'
B'
要证两个三角形相似,目前只有两个途径。一是三角形相似的定义,(条件较多,不常用);二是平行定理。
D
E
1
为了使用它,就必须创造具备定理的基本图形的
条件。怎样创造呢?
规范推理
D
E
A′
B′
C′
A
B
C
在△ABC的边AB上截取
AD=A’
B’
,过点D作DE∥BC,
交AC于点E.则
△ADE∽△ABC
∴∠ADE=∠B
∵
∠B=∠B’
∴∠ADE=∠B’
又∵
AD=A’B’∠
A=∠A’
∴△ADE≌△A’B’C’
(ASA)
∴△
A’B’C’
∽△ABC
证明:
我们可以得到:相似三角形的判定定理1
如果一个三角形的两个角分别与另一个三角形的两个角对应相等.那么这两个三角形相似.
可简单说成:两个角对应相等的两个三角形相似
得出新知
A
B
C
A'
C'
B'
∠A=∠A′
∠
B=∠B′
△ABC∽△
A’B’C’
符号语言表示为:
∵
∴
想一想:
1、△ABC和△A′B′C′中∠A=80°、∠B=40°、∠A′=80°、∠C′=60°.那么这两个三角形相似吗?
2、等边三角形都相似吗?
3、一个锐角对应相等的两个直角三角形相似吗?
4、各有一内角为400的两个等腰三角形相似吗?
5、各一个内角为
100°的两个等腰三角形相似吗?
四、辨析应用,方法提炼
例.
如图,△ABC中,
DE∥BC,EF∥AB,
试说明△ADE∽△EFC.
A
E
F
B
C
D
解:
∵
DE∥BC,EF∥AB(已知),
∴
∠ADE=∠B=∠EFC
(两直线平行,同位角相等)
∠AED=∠C.
(两直线平行,同位角相等)
∴
△ADE∽△EFC.
(两个角分别对应相等的两个三角形相似.)
A
B
D
C
图
3
填一填
(1)如图3,点D在AB上,当
=
时,
△ACD∽△ABC。
(2)如图4,已知点E在AC上,若点D在AB上,则满足条件
,就可以使△ADE与原△ABC相似。
●
A
B
C
E
图
4
∠
ACD
∠B
(或者∠
ACB=∠
ADB)
DE//BC
D
(或者∠
C=∠
ADE)
(或者∠
B=∠
ADE)
D
例、在四边形ABCD中,AC平分∠DAB,∠ACD=∠ABC。求证:AC2=AB·AD
A
B
C
D
即:AC2=AB·AD
A
B
C
D
E
例.已知D、E分别是△ABC的边AB,AC上的点,若∠A=35°,
∠C=85°,∠AED=60
°则AD·AB=
AE·AC
85°
35°
60°
85°
即:AD·AB=
AE·AC
如图,C是线段BD上的一点,AB⊥BD.ED⊥BD.AC⊥EC。求证:△ABC∽△CDE
E
A
1
B
C
D
2
证明:
∵AB⊥BDED⊥BD
∴∠ABC=∠CDE=90°
∴∠1+∠A=90°
∵AC⊥EC
∴∠1+∠2=90°
∴∠A=∠2
∴△ABC∽△CDE
例题赏析
1、已知:在△ABC∽△A1B1C1,
△A1B1C1∽△A2B2C2
,那么△ABC与△A2B2C2有什么关系,为什么?
证明:∵
△ABC∽△A1B1C1
∴∠A=
∠A1,∠B=
∠B1
∵
△A1B1C1∽△A2B2C2
∴∠A1=
∠A2,∠B1=
∠B2
∴∠A=
∠A2,∠B=
∠B2
∵
△ABC∽△A2B2C2
三角形相似的传递性
练一练:
七、巩固新知
2、写出图中的相似三角形:
(1)条件:
DE∥BC
EF∥AB
(2)条件
∠A=36°
AB=AC
BD平分∠ABC
△ADE∽△ABC∽△EFC
△ABC∽△BDC
A
B
C
D
E
F
A
B
C
D
36°
五、反思总结,知识梳理
回顾一下我们这节课学习了哪些主要知识?
1、相似三角形的判定定理1;
2、思想方法:类比、转化、分类讨论
