16.1.1《从分数到分式》
文档属性
| 名称 | 16.1.1《从分数到分式》 |

|
|
| 格式 | zip | ||
| 文件大小 | 467.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-15 10:46:57 | ||
图片预览







文档简介
(共22张PPT)
第1课时
我们学过的代数式中有单项式、多项式、整式,请你判定下列说法是否正确
(1)2x是单项式,也是整式 ( )
(2) 和0都是单项式,也都是整式 ( )
(3)2x-1是多项式,也是整式 ( )
(4) 是多项式,也是整式 ( )
单项式、多项式统称整式
(一)问题情景
整式
多项式
单项式、多项式统称整式
单项式
(5) 是单项式,也是整式 ( )
(6) 是多项式,也是整式 ( )
既不是单项式又不是多项式,即不是整式的另一类式子----新旧知识的碰撞
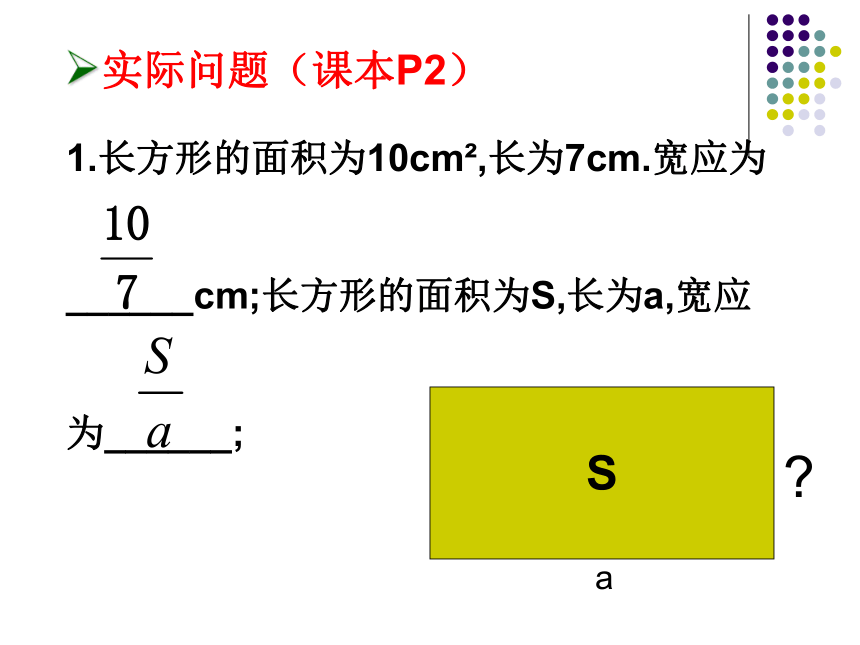
1.长方形的面积为10cm ,长为7cm.宽应为
______cm;长方形的面积为S,长为a,宽应
为______;
S
a
实际问题(课本P2)
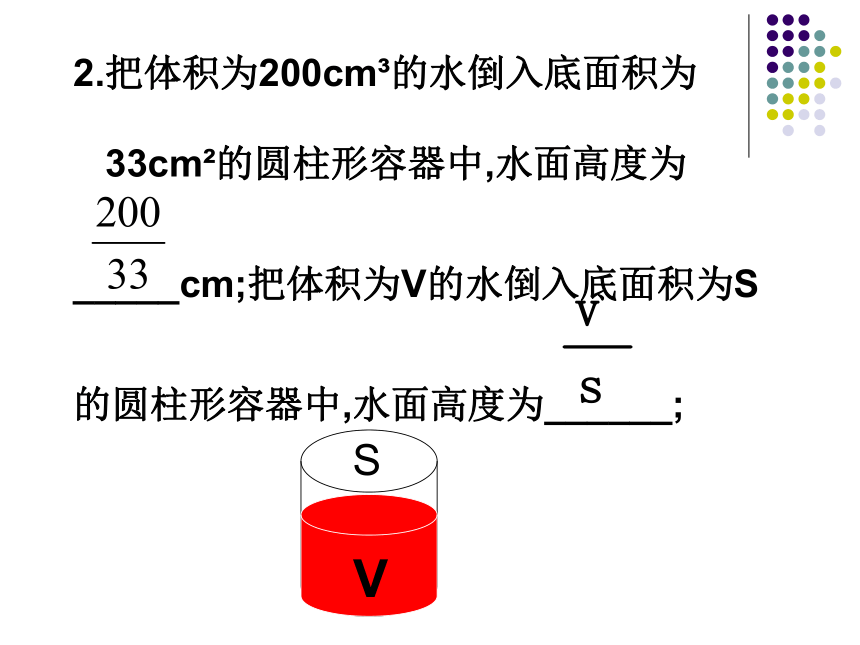
2.把体积为200cm 的水倒入底面积为
33cm 的圆柱形容器中,水面高度为
_____cm;把体积为V的水倒入底面积为S
的圆柱形容器中,水面高度为______;
V
S
观察式子 和 , 和 ,辨析它们的相同点和不同点.
都具有分数的形式
相同点
不同点
(观察分母)
分母中有无字母
辨析、思考
两个整式相除的商,分数线可以理解为除号
一般地,如果A、B都表示整式,且B中含有字母,那么称 为分式。其中A叫做分式的分子,B为分式的分母。
注意:分式是不同于整式的另一类有理式,且分母中含有字母是分式的一大特点。
(二)形成概念
整式
多项式
单项式
分式
有理式
例1(补充)下面的式子哪些是分式?
(三)例题设计
探究(1)(补充)
思考1 根据下列 的值填表.
……
……
……
……
……
……
0
1
问题: 分式 在什么条件下有意义?
结论:(1)分式中B≠0时,分式 有意义;
(2)分式中B=0,分式 无意义.
该怎样做?
变式练习 若把题目要求改为:“当 取何值时下列分式无意义?”
例2 (补充)当x取什么值时,下列分式有意义?
; (2) ;
(3) ; (4) .
(三)例题设计
思考2 分式 在什么条件下值为0?
归纳 分式的值要为0,需满足的条件是:分子的值等于0且分母值不为0.
仅仅是 就可以了吗?
例3(补充)当 是什么值时,分式的 值是0?
探究(2)
(2) 当x为何值时,分式有意义
(1) 当x为何值时,分式无意义
例4(补充).已知分式 ,
(3) 当x为何值时,分式的值为零
三种形式
的值为负;
的值为正.
当x 时,
例5(补充)当x 时,
探究(3)附加问题
思考3 分式 在什么条件下值为正?
分式 在什么条件下值为负?
归纳 (1)当A、B同号时,分式 的值为正;
(2)当A、B同号时,分式 的值为负.
1.列式表示下列各量:
(1)某村有n个人,耕地40公顷,人均耕地
面积为_____________公顷;
(2)△ABC的面积为S,BC边长为a,
高AD为_____________;
(3)一辆汽车行驶 千米用 小时,它的平均
速度为____千米/时;一列火车行驶 千米比
这辆汽车少用t小时,它的平均车速为____千米/时.
课本P4 练习 1-3
(四)配套练习(课本P4+例1+补充)
(课本P3例1-当作练习)
练习:下列各式中,无论x取何值,分式都有意义的是( )
C.
A.
B.
D.
(补充)
★ 学习内容:分式的概念 数学思想:类比
1.分式 有意义的条件是__________.
3.分式 值为0的条件是_____________.
2.分式 无意义的条件是__________.
4.分式 值为正的条件是_____________.
5.分式 值为负的条件是_____________.
(五)归纳小结(3个+2点)
分式有意义的条件:
分式的分母不等于零
分式的值为零的条件:
分式的分子等于零
且分母不等于零
分式无意义的条件:
分式的分母等于零
分式的值为正或负的条件:
同号得正,异号得负
(六)课后作业
课本P8-1(直接写在课本) 课本P8-2,3,13
(一)创设情景(复习+问题)
(二)形成概念(类比+归纳)
(三)例题设计(原1+补3)
(四)配套练习(课本P4+补充)
(五)归纳小结(3点+1个)
(六)课后作业(课本P8-2,3,8,13)
四、教学过程六环节
问题 :一艘轮船在静水中的最大航速是20千米/时,它沿江以最大船速顺流航行100千米所用时间,与以最大航速逆流航行60千米所用的时间相等.江水的流速是多少
附带说明:
2、类似,应用分式表示的实际问题待学习 分式的加减乘除乘方运算后再处理,安排在第9课时进行
1、章头问题移到分式方程处理
第1课时
我们学过的代数式中有单项式、多项式、整式,请你判定下列说法是否正确
(1)2x是单项式,也是整式 ( )
(2) 和0都是单项式,也都是整式 ( )
(3)2x-1是多项式,也是整式 ( )
(4) 是多项式,也是整式 ( )
单项式、多项式统称整式
(一)问题情景
整式
多项式
单项式、多项式统称整式
单项式
(5) 是单项式,也是整式 ( )
(6) 是多项式,也是整式 ( )
既不是单项式又不是多项式,即不是整式的另一类式子----新旧知识的碰撞
1.长方形的面积为10cm ,长为7cm.宽应为
______cm;长方形的面积为S,长为a,宽应
为______;
S
a
实际问题(课本P2)
2.把体积为200cm 的水倒入底面积为
33cm 的圆柱形容器中,水面高度为
_____cm;把体积为V的水倒入底面积为S
的圆柱形容器中,水面高度为______;
V
S
观察式子 和 , 和 ,辨析它们的相同点和不同点.
都具有分数的形式
相同点
不同点
(观察分母)
分母中有无字母
辨析、思考
两个整式相除的商,分数线可以理解为除号
一般地,如果A、B都表示整式,且B中含有字母,那么称 为分式。其中A叫做分式的分子,B为分式的分母。
注意:分式是不同于整式的另一类有理式,且分母中含有字母是分式的一大特点。
(二)形成概念
整式
多项式
单项式
分式
有理式
例1(补充)下面的式子哪些是分式?
(三)例题设计
探究(1)(补充)
思考1 根据下列 的值填表.
……
……
……
……
……
……
0
1
问题: 分式 在什么条件下有意义?
结论:(1)分式中B≠0时,分式 有意义;
(2)分式中B=0,分式 无意义.
该怎样做?
变式练习 若把题目要求改为:“当 取何值时下列分式无意义?”
例2 (补充)当x取什么值时,下列分式有意义?
; (2) ;
(3) ; (4) .
(三)例题设计
思考2 分式 在什么条件下值为0?
归纳 分式的值要为0,需满足的条件是:分子的值等于0且分母值不为0.
仅仅是 就可以了吗?
例3(补充)当 是什么值时,分式的 值是0?
探究(2)
(2) 当x为何值时,分式有意义
(1) 当x为何值时,分式无意义
例4(补充).已知分式 ,
(3) 当x为何值时,分式的值为零
三种形式
的值为负;
的值为正.
当x 时,
例5(补充)当x 时,
探究(3)附加问题
思考3 分式 在什么条件下值为正?
分式 在什么条件下值为负?
归纳 (1)当A、B同号时,分式 的值为正;
(2)当A、B同号时,分式 的值为负.
1.列式表示下列各量:
(1)某村有n个人,耕地40公顷,人均耕地
面积为_____________公顷;
(2)△ABC的面积为S,BC边长为a,
高AD为_____________;
(3)一辆汽车行驶 千米用 小时,它的平均
速度为____千米/时;一列火车行驶 千米比
这辆汽车少用t小时,它的平均车速为____千米/时.
课本P4 练习 1-3
(四)配套练习(课本P4+例1+补充)
(课本P3例1-当作练习)
练习:下列各式中,无论x取何值,分式都有意义的是( )
C.
A.
B.
D.
(补充)
★ 学习内容:分式的概念 数学思想:类比
1.分式 有意义的条件是__________.
3.分式 值为0的条件是_____________.
2.分式 无意义的条件是__________.
4.分式 值为正的条件是_____________.
5.分式 值为负的条件是_____________.
(五)归纳小结(3个+2点)
分式有意义的条件:
分式的分母不等于零
分式的值为零的条件:
分式的分子等于零
且分母不等于零
分式无意义的条件:
分式的分母等于零
分式的值为正或负的条件:
同号得正,异号得负
(六)课后作业
课本P8-1(直接写在课本) 课本P8-2,3,13
(一)创设情景(复习+问题)
(二)形成概念(类比+归纳)
(三)例题设计(原1+补3)
(四)配套练习(课本P4+补充)
(五)归纳小结(3点+1个)
(六)课后作业(课本P8-2,3,8,13)
四、教学过程六环节
问题 :一艘轮船在静水中的最大航速是20千米/时,它沿江以最大船速顺流航行100千米所用时间,与以最大航速逆流航行60千米所用的时间相等.江水的流速是多少
附带说明:
2、类似,应用分式表示的实际问题待学习 分式的加减乘除乘方运算后再处理,安排在第9课时进行
1、章头问题移到分式方程处理
