1.1.2 菱形的性质与判定2 课件(共33张PPT)
文档属性
| 名称 | 1.1.2 菱形的性质与判定2 课件(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-30 07:37:47 | ||
图片预览




文档简介
(共33张PPT)
1.1.2
菱形的性质与判定2
第一章
特殊平行四边形
2021-2022学年九年级数学上册同步(北师版)
1.理解并掌握菱形的判定方法.
2.会用这些判定方法进行有关的论证和计算.
3.经历探索菱形判定条件的过程,领会菱形的概念以及判定方法,发展学生主动探究的思想并了解说理的基本方法.
学习目标
复习与回顾:
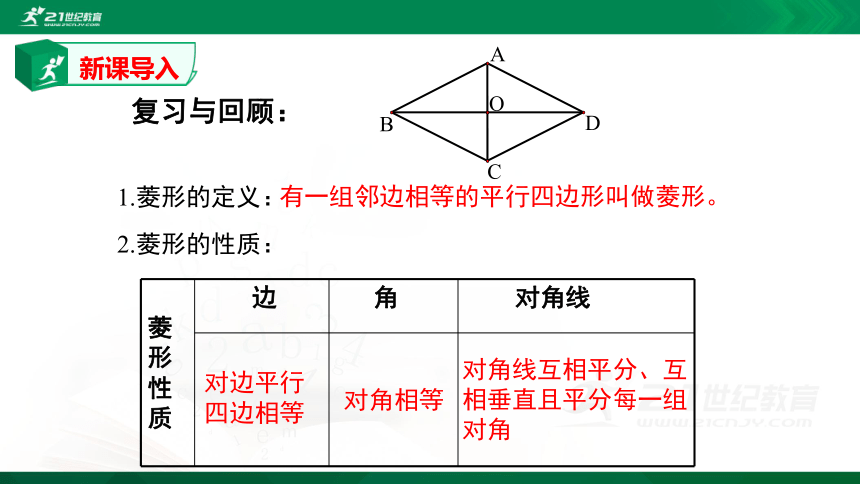
1.菱形的定义:
2.菱形的性质:
有一组邻边相等的平行四边形叫做菱形。
?
?
菱形性质
边
角
对角线
对边平行
四边相等
对角相等
对角线互相平分、互相垂直且平分每一组对角
D
O
A
C
B
新课导入
创设情境
汶川地震后,全国各界组织发起“绿丝带行动”,号召人民为四川受灾的人们祈福。人们将绿丝带剪成小段,并用别针将折叠好的绿丝带别在胸前,如图所示,绿丝带重叠部分形成的图形是一个漂亮的菱形。你知道是怎样判断它是一个菱形的吗?
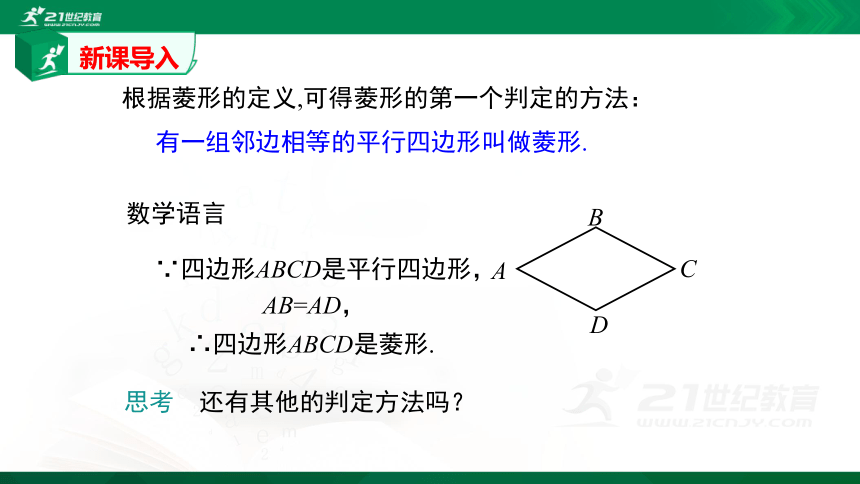
根据菱形的定义,可得菱形的第一个判定的方法:
AB=AD,
∵四边形ABCD是平行四边形,
∴四边形ABCD是菱形.
数学语言
有一组邻边相等的平行四边形叫做菱形.
A
B
C
D
思考
还有其他的判定方法吗?
新课导入
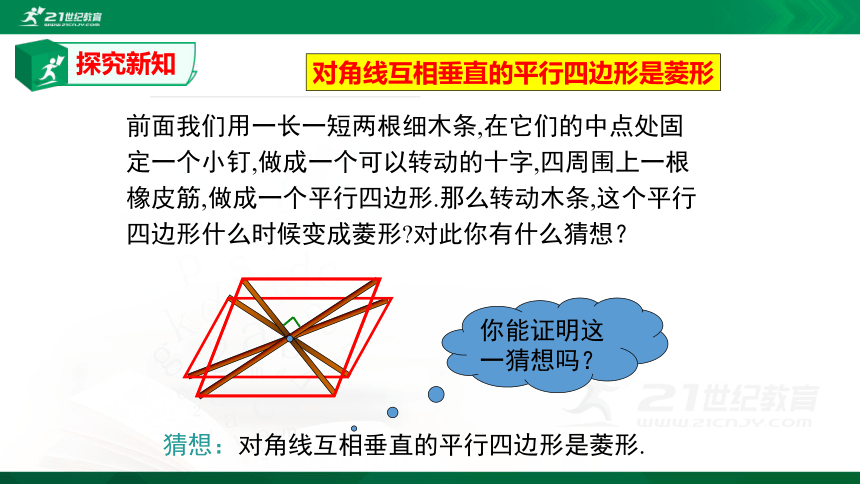
对角线互相垂直的平行四边形是菱形
前面我们用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个平行四边形.那么转动木条,这个平行四边形什么时候变成菱形?对此你有什么猜想?
猜想:对角线互相垂直的平行四边形是菱形.
你能证明这一猜想吗?
探究新知
A
B
C
O
D
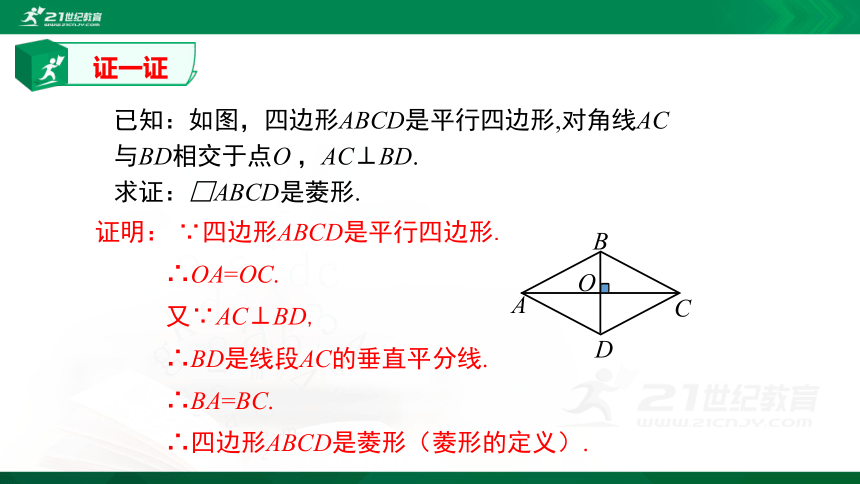
已知:如图,四边形ABCD是平行四边形,对角线AC与BD相交于点O
,AC⊥BD.
求证:□ABCD是菱形.
证明:
∵四边形ABCD是平行四边形.
∴OA=OC.
又∵AC⊥BD,
∴BD是线段AC的垂直平分线.
∴BA=BC.
∴四边形ABCD是菱形(菱形的定义).
证一证
对角线互相垂直的平行四边形是菱形
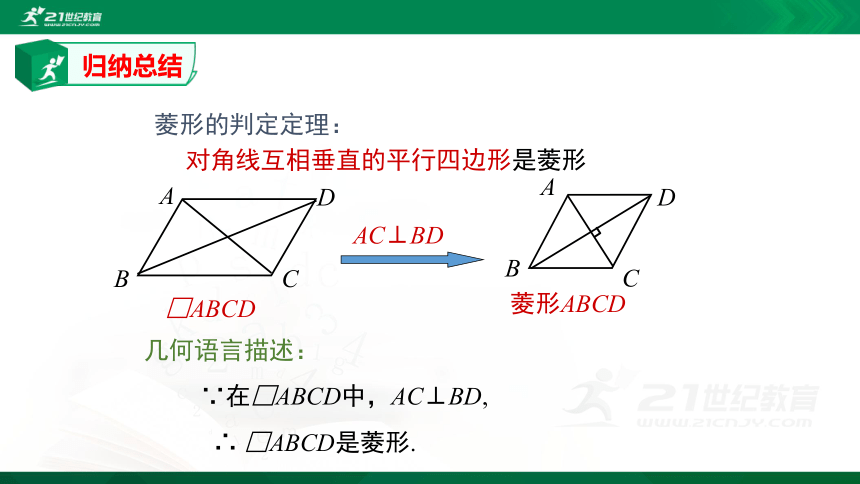
AC⊥BD
几何语言描述:
∵在□ABCD中,AC⊥BD,
∴
□ABCD是菱形.
A
B
C
D
菱形ABCD
A
B
C
D
□ABCD
菱形的判定定理:
归纳总结
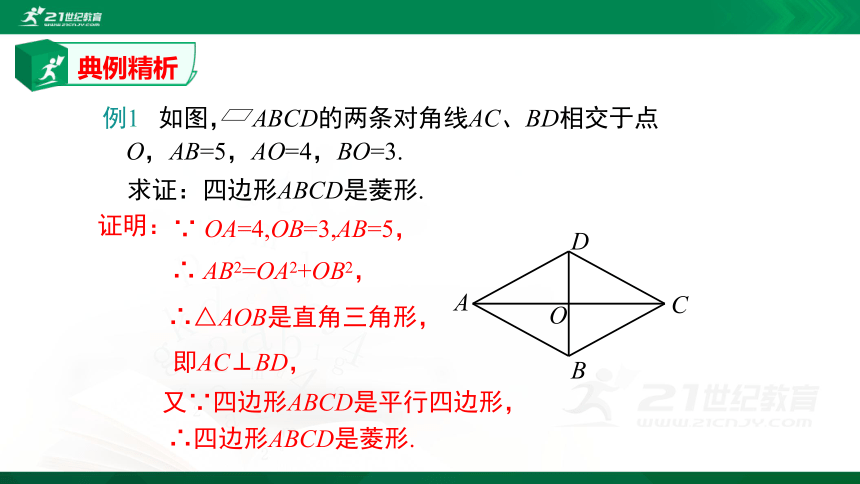
例1
如图,
ABCD的两条对角线AC、BD相交于点O,AB=5,AO=4,BO=3.
求证:四边形ABCD是菱形.
A
B
C
D
O
又∵四边形ABCD是平行四边形,
∵
OA=4,OB=3,AB=5,
证明:
即AC⊥BD,
∴
AB2=OA2+OB2,
∴△AOB是直角三角形,
典例精析
∴四边形ABCD是菱形.
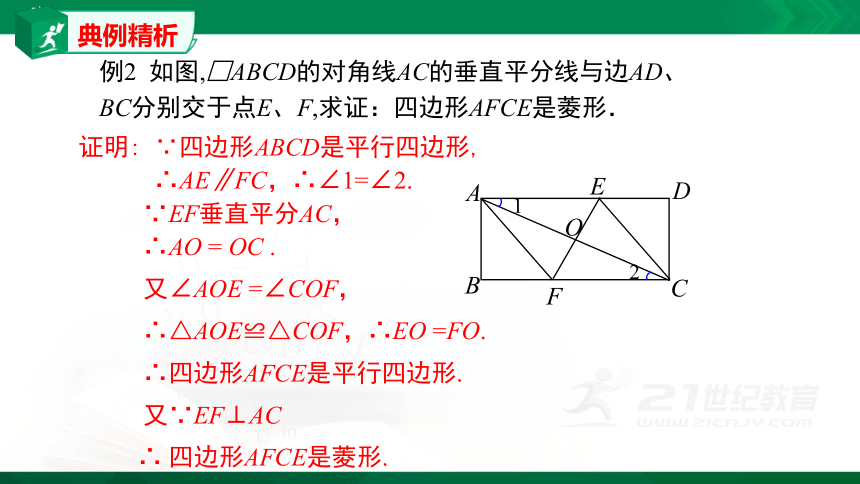
例2
如图,□ABCD的对角线AC的垂直平分线与边AD、BC分别交于点E、F,求证:四边形AFCE是菱形.
A
B
C
D
E
F
O
1
2
证明:
∵四边形ABCD是平行四边形,
∴AE∥FC,∴∠1=∠2.
∵EF垂直平分AC,
∴AO
=
OC
.
又∠AOE
=∠COF,
∴△AOE≌△COF,∴EO
=FO.
∴四边形AFCE是平行四边形.
又∵EF⊥AC
∴
四边形AFCE是菱形.
典例精析
在四边形ABCD中,对角线AC,BD互相平分,若添加一个条件使得四边形ABCD是菱形,则这个条件可以是
(
)
A.∠ABC=90°
B.AC⊥BD
C.AB=CD
D.AB∥CD
B
针对练习
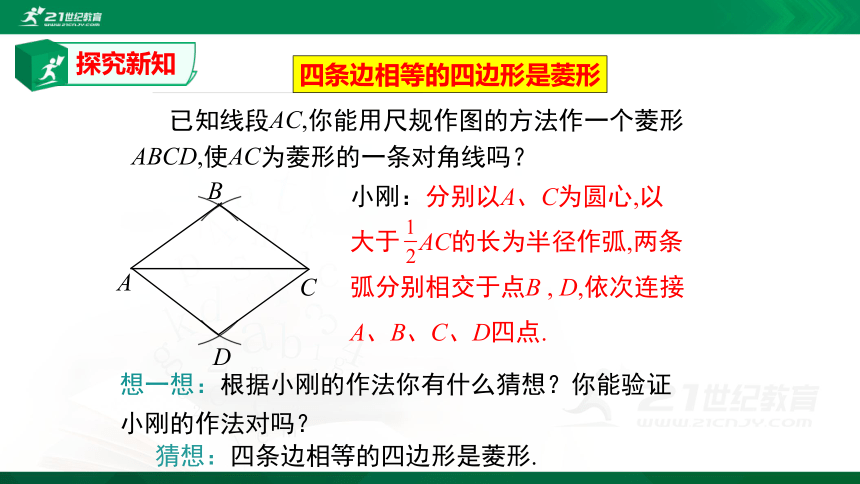
四条边相等的四边形是菱形
小刚:分别以A、C为圆心,以大于
AC的长为半径作弧,两条
弧分别相交于点B
,
D,依次连接A、B、C、D四点.
已知线段AC,你能用尺规作图的方法作一个菱形ABCD,使AC为菱形的一条对角线吗?
C
A
B
D
想一想:根据小刚的作法你有什么猜想?你能验证小刚的作法对吗?
猜想:四条边相等的四边形是菱形.
探究新知
证明:∵AB=BC=CD=AD;
∴AB=CD
,
BC=AD.
∴四边形ABCD是平行四边形.
又∵AB=BC,
∴四边形ABCD是菱形.
A
B
C
D
已知:如图,四边形ABCD中,AB=BC=CD=AD.
求证:四边形ABCD是菱形.
证一证
四条边都相等的四边形是菱形
AB=BC=CD=AD
几何语言描述:
∵在四边形ABCD中,AB=BC=CD=AD,
∴四边形
ABCD是菱形.
A
B
C
D
菱形ABCD
菱形的判定定理:
归纳总结
四边形ABCD
A
B
C
D
下列命题中正确的是
(
)
A.一组邻边相等的四边形是菱形
B.三条边相等的四边形是菱形
C.四条边相等的四边形是菱形
D.四个角相等的四边形是菱形
C
针对练习
证明:
∵
∠1=
∠2,
又∵AE=AC,AD=AD,
∴
△ACD≌
△AED
(SAS).
同理△ACF≌△AEF(SAS)
.
∴CD=ED,
CF=EF.
又∵EF=ED,∴CD=ED=CF=EF,
∴四边形ABCD是菱形.
2
例3
如图,在△ABC中,
AD是角平分线,点E、F分别在
AB、
AD上,且AE=AC,EF
=
ED.
求证:四边形CDEF是菱形.
A
C
B
E
D
F
1
典例精析
例4
如图,在△ABC中,∠B=90°,AB=6cm,BC=8cm.将△ABC沿射线BC方向平移10cm,得到△DEF,A,B,C的对应点分别是D,E,F,连接AD.求证:四边形ACFD是菱形.
证明:由平移变换的性质得CF=AD=10cm,DF=AC.
∵∠B=90°,AB=6cm,BC=8cm,
∴AC=DF=AD=CF=10cm,
∴四边形ACFD是菱形.
四边形的条件中存在多个关于边的等量关系时,运用四条边都相等来判定一个四边形是菱形比较方便.
归纳
典例精析
由菱形的性质:“每条对角线平分一组对角”,我们还可以得到判定菱形的方法:
每条对角线平分一组对角的四边形是菱形.
对此感兴趣的同学,可以试着用逻辑推理的方法进行证明.
拓展训练
1、有一组邻边相等的平行四边形叫做菱形.
2、对角线互相垂直的平行四边形是菱形.
(对角线互相垂直平分的四边形是菱形.)
3、有四条边相等的四边形是菱形.
菱形的判定方法
归纳总结
4、每条对角线平分一组对角的四边形是菱形.
文字语言
图形语言
符号语言
判定法一
判定
法二
判定法三
A
B
C
D
∵AB=BC=CD=DA
∴四边形ABCD是菱形
∵在□ABCD中
AC⊥BD
∴四边形ABCD是菱形
∵在□ABCD中
AB=AD
∴四边形ABCD是菱形
A
B
C
D
O
A
B
C
D
一组邻边相等的平行四边形是菱形
对角线互相垂直的平行四边形是菱形
四边相等的四边形是菱形
菱形的三种判定方法
归纳总结
一组邻边相等
对角线互相垂直
四条边相等
五种判定方法
四边形
平行四边形
菱形
菱形的判定方法:
归纳总结
请你动脑筋
把两张等宽的纸条交叉重叠在一起,你能判断重叠部分ABCD的形状吗?
A
C
D
B
想一想
请你动脑筋
D
C
B
A
1.判断下列说法是否正确
(1)对角线互相垂直的四边形是菱形;
(2)对角线互相垂直且平分的四边形是菱形;
(3)对角线互相垂直,且有一组邻边相等的
四边形是菱形;
(4)两条邻边相等,且一条对角线平分一组
对角的四边形是菱形.
√
╳
╳
╳
2.一边长为5cm平行四边形的两条对角线的长分别为
24cm和26cm,那么平行四边形的面积是
.
312cm2
课堂练习
3.下列条件中,不能判定四边形ABCD为菱形的是
( )
A.
AC⊥BD
,AC与BD互相平分
B.
AB=BC=CD=DA
C.
AB=BC,AD=CD,AC
⊥BD
D.
AB=CD,AD=BC,AC
⊥BD
A
B
C
O
D
C
4.如图,将△ABC沿BC方向平移得到△DCE,连接AD,下列条件能够判定四边形ACED为菱形的是( )
A.AB=BC
B.AC=BC
C.∠B=60°
D.∠ACB=60°
B
解析:∵将△ABC沿BC方向平移得到△DCE,
∴AC∥DE,AC=DE,
∴四边形ABED为平行四边形.
当AC=BC时,
平行四边形ACED是菱形.
故选B.
5.如图,已知平行四边形ABCD的对角线AC的垂直平分线与边AD、BC分别交于点E、F,求证:四边形AFCE是菱形.
A
B
C
D
E
F
O
1
2
证明:
∵四边形ABCD是平行四边形,
∴AE∥FC.
∴∠1=∠2.
∵EF垂直平分AC,
∴AO
=
OC
.
∴EO
=FO.
∴四边形AFCE是平行四边形.
又∵EF⊥AC
∴
四边形AFCE是菱形.
A
B
C
D
O
E
6.如图,已知平行四边形ABCD的对角线相交于点O,且AB=BD,DE∥AC,CE
∥BD.
求证:四边形OCED是菱形.
证明:∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形,
∵四边形ABCD是平行四边形,AB=BD,
∴OC=OD,
∴四边形OCED是菱形.
7.如图,△ABC中,AC的垂直平分线MN交AB于点D,交AC于点O,CE∥AB交MN于点E,连接AE、CD.
求证:四边形ADCE是菱形.
B
C
A
D
O
E
M
N
【分析】根据垂直平分线的性质可得AE=CE,AD=CD,OA=OC,
∠AOD=∠EOC=90°
.再结合CE∥AB,可证得△ADO≌△CEO,从而根据由一组对边平行且相等知,四边形ADCE是平行四边形.
再结合∠AOD=90°可证得四边形ADCE为菱形.
证明:∵MN是AC的垂直平分线,
∴AE=CE,AD=CD,OA=OC,∠AOD=∠EOC=90°.
∵CE∥AB,
∴∠DAO=∠ECO,
∴△ADO≌△CEO(ASA).
∴AD=CE,OD=OE,
∵OD=OE,OA=OC,∴四边形ADCE是平行四边形
又∵∠AOD=90°,∴四边形ADCE是菱形.
A
D
O
E
M
B
C
有一组邻边相等的平行四边形是菱形.
对角线互相垂直的平行四边形是菱形.
四边相等的四边形是菱形.
运用定理进行计算和证明
菱形的判定
定义法
判定定理
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
1.1.2
菱形的性质与判定2
第一章
特殊平行四边形
2021-2022学年九年级数学上册同步(北师版)
1.理解并掌握菱形的判定方法.
2.会用这些判定方法进行有关的论证和计算.
3.经历探索菱形判定条件的过程,领会菱形的概念以及判定方法,发展学生主动探究的思想并了解说理的基本方法.
学习目标
复习与回顾:
1.菱形的定义:
2.菱形的性质:
有一组邻边相等的平行四边形叫做菱形。
?
?
菱形性质
边
角
对角线
对边平行
四边相等
对角相等
对角线互相平分、互相垂直且平分每一组对角
D
O
A
C
B
新课导入
创设情境
汶川地震后,全国各界组织发起“绿丝带行动”,号召人民为四川受灾的人们祈福。人们将绿丝带剪成小段,并用别针将折叠好的绿丝带别在胸前,如图所示,绿丝带重叠部分形成的图形是一个漂亮的菱形。你知道是怎样判断它是一个菱形的吗?
根据菱形的定义,可得菱形的第一个判定的方法:
AB=AD,
∵四边形ABCD是平行四边形,
∴四边形ABCD是菱形.
数学语言
有一组邻边相等的平行四边形叫做菱形.
A
B
C
D
思考
还有其他的判定方法吗?
新课导入
对角线互相垂直的平行四边形是菱形
前面我们用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个平行四边形.那么转动木条,这个平行四边形什么时候变成菱形?对此你有什么猜想?
猜想:对角线互相垂直的平行四边形是菱形.
你能证明这一猜想吗?
探究新知
A
B
C
O
D
已知:如图,四边形ABCD是平行四边形,对角线AC与BD相交于点O
,AC⊥BD.
求证:□ABCD是菱形.
证明:
∵四边形ABCD是平行四边形.
∴OA=OC.
又∵AC⊥BD,
∴BD是线段AC的垂直平分线.
∴BA=BC.
∴四边形ABCD是菱形(菱形的定义).
证一证
对角线互相垂直的平行四边形是菱形
AC⊥BD
几何语言描述:
∵在□ABCD中,AC⊥BD,
∴
□ABCD是菱形.
A
B
C
D
菱形ABCD
A
B
C
D
□ABCD
菱形的判定定理:
归纳总结
例1
如图,
ABCD的两条对角线AC、BD相交于点O,AB=5,AO=4,BO=3.
求证:四边形ABCD是菱形.
A
B
C
D
O
又∵四边形ABCD是平行四边形,
∵
OA=4,OB=3,AB=5,
证明:
即AC⊥BD,
∴
AB2=OA2+OB2,
∴△AOB是直角三角形,
典例精析
∴四边形ABCD是菱形.
例2
如图,□ABCD的对角线AC的垂直平分线与边AD、BC分别交于点E、F,求证:四边形AFCE是菱形.
A
B
C
D
E
F
O
1
2
证明:
∵四边形ABCD是平行四边形,
∴AE∥FC,∴∠1=∠2.
∵EF垂直平分AC,
∴AO
=
OC
.
又∠AOE
=∠COF,
∴△AOE≌△COF,∴EO
=FO.
∴四边形AFCE是平行四边形.
又∵EF⊥AC
∴
四边形AFCE是菱形.
典例精析
在四边形ABCD中,对角线AC,BD互相平分,若添加一个条件使得四边形ABCD是菱形,则这个条件可以是
(
)
A.∠ABC=90°
B.AC⊥BD
C.AB=CD
D.AB∥CD
B
针对练习
四条边相等的四边形是菱形
小刚:分别以A、C为圆心,以大于
AC的长为半径作弧,两条
弧分别相交于点B
,
D,依次连接A、B、C、D四点.
已知线段AC,你能用尺规作图的方法作一个菱形ABCD,使AC为菱形的一条对角线吗?
C
A
B
D
想一想:根据小刚的作法你有什么猜想?你能验证小刚的作法对吗?
猜想:四条边相等的四边形是菱形.
探究新知
证明:∵AB=BC=CD=AD;
∴AB=CD
,
BC=AD.
∴四边形ABCD是平行四边形.
又∵AB=BC,
∴四边形ABCD是菱形.
A
B
C
D
已知:如图,四边形ABCD中,AB=BC=CD=AD.
求证:四边形ABCD是菱形.
证一证
四条边都相等的四边形是菱形
AB=BC=CD=AD
几何语言描述:
∵在四边形ABCD中,AB=BC=CD=AD,
∴四边形
ABCD是菱形.
A
B
C
D
菱形ABCD
菱形的判定定理:
归纳总结
四边形ABCD
A
B
C
D
下列命题中正确的是
(
)
A.一组邻边相等的四边形是菱形
B.三条边相等的四边形是菱形
C.四条边相等的四边形是菱形
D.四个角相等的四边形是菱形
C
针对练习
证明:
∵
∠1=
∠2,
又∵AE=AC,AD=AD,
∴
△ACD≌
△AED
(SAS).
同理△ACF≌△AEF(SAS)
.
∴CD=ED,
CF=EF.
又∵EF=ED,∴CD=ED=CF=EF,
∴四边形ABCD是菱形.
2
例3
如图,在△ABC中,
AD是角平分线,点E、F分别在
AB、
AD上,且AE=AC,EF
=
ED.
求证:四边形CDEF是菱形.
A
C
B
E
D
F
1
典例精析
例4
如图,在△ABC中,∠B=90°,AB=6cm,BC=8cm.将△ABC沿射线BC方向平移10cm,得到△DEF,A,B,C的对应点分别是D,E,F,连接AD.求证:四边形ACFD是菱形.
证明:由平移变换的性质得CF=AD=10cm,DF=AC.
∵∠B=90°,AB=6cm,BC=8cm,
∴AC=DF=AD=CF=10cm,
∴四边形ACFD是菱形.
四边形的条件中存在多个关于边的等量关系时,运用四条边都相等来判定一个四边形是菱形比较方便.
归纳
典例精析
由菱形的性质:“每条对角线平分一组对角”,我们还可以得到判定菱形的方法:
每条对角线平分一组对角的四边形是菱形.
对此感兴趣的同学,可以试着用逻辑推理的方法进行证明.
拓展训练
1、有一组邻边相等的平行四边形叫做菱形.
2、对角线互相垂直的平行四边形是菱形.
(对角线互相垂直平分的四边形是菱形.)
3、有四条边相等的四边形是菱形.
菱形的判定方法
归纳总结
4、每条对角线平分一组对角的四边形是菱形.
文字语言
图形语言
符号语言
判定法一
判定
法二
判定法三
A
B
C
D
∵AB=BC=CD=DA
∴四边形ABCD是菱形
∵在□ABCD中
AC⊥BD
∴四边形ABCD是菱形
∵在□ABCD中
AB=AD
∴四边形ABCD是菱形
A
B
C
D
O
A
B
C
D
一组邻边相等的平行四边形是菱形
对角线互相垂直的平行四边形是菱形
四边相等的四边形是菱形
菱形的三种判定方法
归纳总结
一组邻边相等
对角线互相垂直
四条边相等
五种判定方法
四边形
平行四边形
菱形
菱形的判定方法:
归纳总结
请你动脑筋
把两张等宽的纸条交叉重叠在一起,你能判断重叠部分ABCD的形状吗?
A
C
D
B
想一想
请你动脑筋
D
C
B
A
1.判断下列说法是否正确
(1)对角线互相垂直的四边形是菱形;
(2)对角线互相垂直且平分的四边形是菱形;
(3)对角线互相垂直,且有一组邻边相等的
四边形是菱形;
(4)两条邻边相等,且一条对角线平分一组
对角的四边形是菱形.
√
╳
╳
╳
2.一边长为5cm平行四边形的两条对角线的长分别为
24cm和26cm,那么平行四边形的面积是
.
312cm2
课堂练习
3.下列条件中,不能判定四边形ABCD为菱形的是
( )
A.
AC⊥BD
,AC与BD互相平分
B.
AB=BC=CD=DA
C.
AB=BC,AD=CD,AC
⊥BD
D.
AB=CD,AD=BC,AC
⊥BD
A
B
C
O
D
C
4.如图,将△ABC沿BC方向平移得到△DCE,连接AD,下列条件能够判定四边形ACED为菱形的是( )
A.AB=BC
B.AC=BC
C.∠B=60°
D.∠ACB=60°
B
解析:∵将△ABC沿BC方向平移得到△DCE,
∴AC∥DE,AC=DE,
∴四边形ABED为平行四边形.
当AC=BC时,
平行四边形ACED是菱形.
故选B.
5.如图,已知平行四边形ABCD的对角线AC的垂直平分线与边AD、BC分别交于点E、F,求证:四边形AFCE是菱形.
A
B
C
D
E
F
O
1
2
证明:
∵四边形ABCD是平行四边形,
∴AE∥FC.
∴∠1=∠2.
∵EF垂直平分AC,
∴AO
=
OC
.
∴EO
=FO.
∴四边形AFCE是平行四边形.
又∵EF⊥AC
∴
四边形AFCE是菱形.
A
B
C
D
O
E
6.如图,已知平行四边形ABCD的对角线相交于点O,且AB=BD,DE∥AC,CE
∥BD.
求证:四边形OCED是菱形.
证明:∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形,
∵四边形ABCD是平行四边形,AB=BD,
∴OC=OD,
∴四边形OCED是菱形.
7.如图,△ABC中,AC的垂直平分线MN交AB于点D,交AC于点O,CE∥AB交MN于点E,连接AE、CD.
求证:四边形ADCE是菱形.
B
C
A
D
O
E
M
N
【分析】根据垂直平分线的性质可得AE=CE,AD=CD,OA=OC,
∠AOD=∠EOC=90°
.再结合CE∥AB,可证得△ADO≌△CEO,从而根据由一组对边平行且相等知,四边形ADCE是平行四边形.
再结合∠AOD=90°可证得四边形ADCE为菱形.
证明:∵MN是AC的垂直平分线,
∴AE=CE,AD=CD,OA=OC,∠AOD=∠EOC=90°.
∵CE∥AB,
∴∠DAO=∠ECO,
∴△ADO≌△CEO(ASA).
∴AD=CE,OD=OE,
∵OD=OE,OA=OC,∴四边形ADCE是平行四边形
又∵∠AOD=90°,∴四边形ADCE是菱形.
A
D
O
E
M
B
C
有一组邻边相等的平行四边形是菱形.
对角线互相垂直的平行四边形是菱形.
四边相等的四边形是菱形.
运用定理进行计算和证明
菱形的判定
定义法
判定定理
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
