5.2.2导数的四则运算法则 课件——2020-2021学年高二下学期数学人教A版(2019)选择性必修二第五章第二节(共25张PPT)
文档属性
| 名称 | 5.2.2导数的四则运算法则 课件——2020-2021学年高二下学期数学人教A版(2019)选择性必修二第五章第二节(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 939.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-31 20:50:38 | ||
图片预览








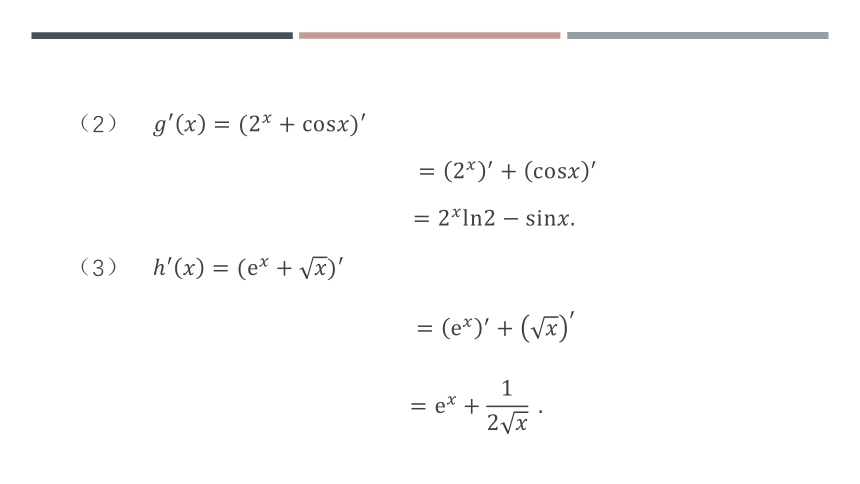
文档简介
(共25张PPT)
导数的四则运算
人教a版选择性必修二
问题1
如何求函数的导数?
导数的定义;
直接通过公式得到基本初等函数的导数.
追问:
学习了哪些基本初等函数的导数?
1.
若则;
2.若
(∈Q,且≠0),则;
3.若,则;
4.若
,则;
5.若
(,
且)
,则;
特别地,若,则;
6.
(,
且),则;
特别地,若,则.
问题2
如何求函数的导数?
目前,我们只能通过定义来求其导数.
设,由导数的定义,
追问:观察,,;
与导数,,.
你有什么发现和猜想?
;.
猜想:.
同样地,.
一般地,对于两个函数的和(或差)的导数,我们有如下法则:
函数和、差的求导运算法则
例1
求下列函数的导数:
(1);
(2);
(3).
解:(1)
(2)
(3)
问题3
以
,为例,计算与,看看是否相等?
,
,
所以.
追问:再验算
与商的导数是否等于它们导数的商?
事实上,对于两个函数的乘积(或商)的导数,我们有如下法则:
函数积、商的求导运算法则
进一步,由函数乘积的导数法则可以得出
也就是说,常数与函数的积的导数,等于常数与函数的导数的积,即:
例2
求下列函数的导数:
;
.
解:(1)
例3
日常生活中的饮用水通常是经过净化的.
随着水的纯净度的提高,所需净化费用不断增加.
已知将吨水净化到纯净度为时所需费用(单位:元)为
求净化到纯净度为和,所需净化费用的瞬时变化率.
问题4
怎样求纯净度为和时,所需净化费用的瞬时变化率?
通过求净化费用函数的导数来解决.
所以,
.
追问:
根据计算结果能得出哪些结论?
净化到纯净度为时净化费用的瞬时变化率是净化到纯净度为时的倍.
即净化到纯净度为98%时净化费用变化的快慢是净化到纯净度为90%时净化费用变化快慢的倍.
问题5
我们学习了哪些知识内容?
函数的和、差、积、商的导数运算法则.
1.
函数的和、差的导数运算法则
2.
函数的积、商的导数运算法则
追问:
你有哪些收获?
运用函数的导数运算法则求函数的导数,比用导数定义求函数的导数要方便很多.
运用导数运算法则可以求很多初等函数的导数,这有助于研究更多函数的性质.
导数的四则运算
人教a版选择性必修二
问题1
如何求函数的导数?
导数的定义;
直接通过公式得到基本初等函数的导数.
追问:
学习了哪些基本初等函数的导数?
1.
若则;
2.若
(∈Q,且≠0),则;
3.若,则;
4.若
,则;
5.若
(,
且)
,则;
特别地,若,则;
6.
(,
且),则;
特别地,若,则.
问题2
如何求函数的导数?
目前,我们只能通过定义来求其导数.
设,由导数的定义,
追问:观察,,;
与导数,,.
你有什么发现和猜想?
;.
猜想:.
同样地,.
一般地,对于两个函数的和(或差)的导数,我们有如下法则:
函数和、差的求导运算法则
例1
求下列函数的导数:
(1);
(2);
(3).
解:(1)
(2)
(3)
问题3
以
,为例,计算与,看看是否相等?
,
,
所以.
追问:再验算
与商的导数是否等于它们导数的商?
事实上,对于两个函数的乘积(或商)的导数,我们有如下法则:
函数积、商的求导运算法则
进一步,由函数乘积的导数法则可以得出
也就是说,常数与函数的积的导数,等于常数与函数的导数的积,即:
例2
求下列函数的导数:
;
.
解:(1)
例3
日常生活中的饮用水通常是经过净化的.
随着水的纯净度的提高,所需净化费用不断增加.
已知将吨水净化到纯净度为时所需费用(单位:元)为
求净化到纯净度为和,所需净化费用的瞬时变化率.
问题4
怎样求纯净度为和时,所需净化费用的瞬时变化率?
通过求净化费用函数的导数来解决.
所以,
.
追问:
根据计算结果能得出哪些结论?
净化到纯净度为时净化费用的瞬时变化率是净化到纯净度为时的倍.
即净化到纯净度为98%时净化费用变化的快慢是净化到纯净度为90%时净化费用变化快慢的倍.
问题5
我们学习了哪些知识内容?
函数的和、差、积、商的导数运算法则.
1.
函数的和、差的导数运算法则
2.
函数的积、商的导数运算法则
追问:
你有哪些收获?
运用函数的导数运算法则求函数的导数,比用导数定义求函数的导数要方便很多.
运用导数运算法则可以求很多初等函数的导数,这有助于研究更多函数的性质.
